Monosynaptic Scalable Architecture Revealed by Transsynaptic Rabies Tracing
Daniel Fürth
Meletis Lab
Network for Networks
12 Feb 2016
daniel.furth@ki.se
- Yang Xuan
- Ourania Tzortzi
- Iakovos Lazardis
- Konstantinos Meletis
- DMC lab
Acknowledgement
Reconstructing brain from sectioned tissue
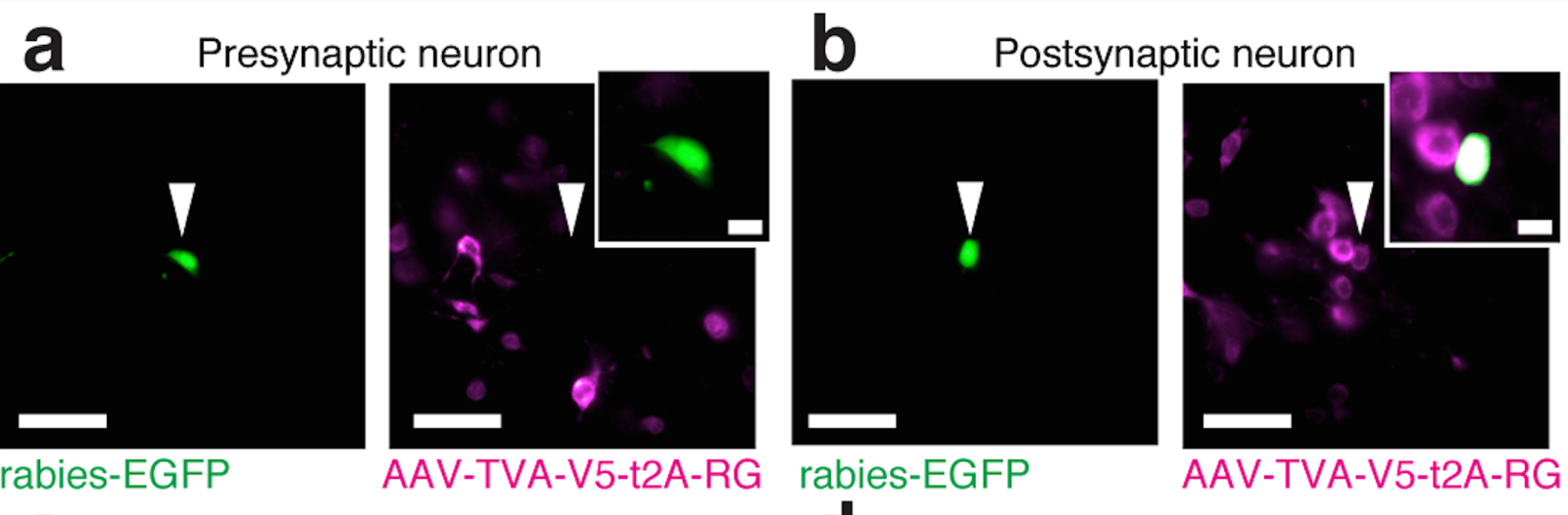
Tracing the network
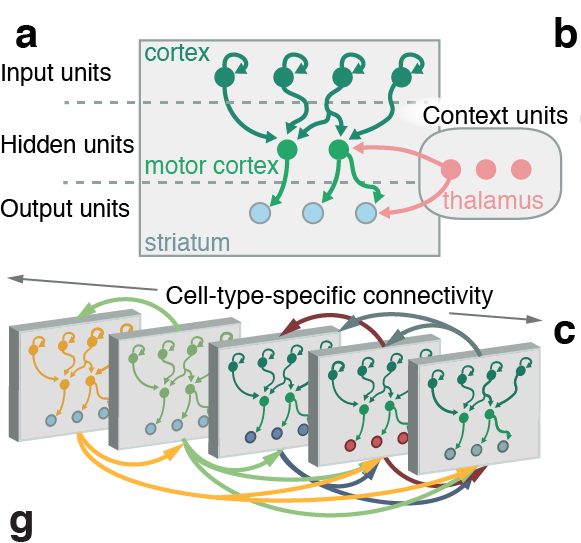
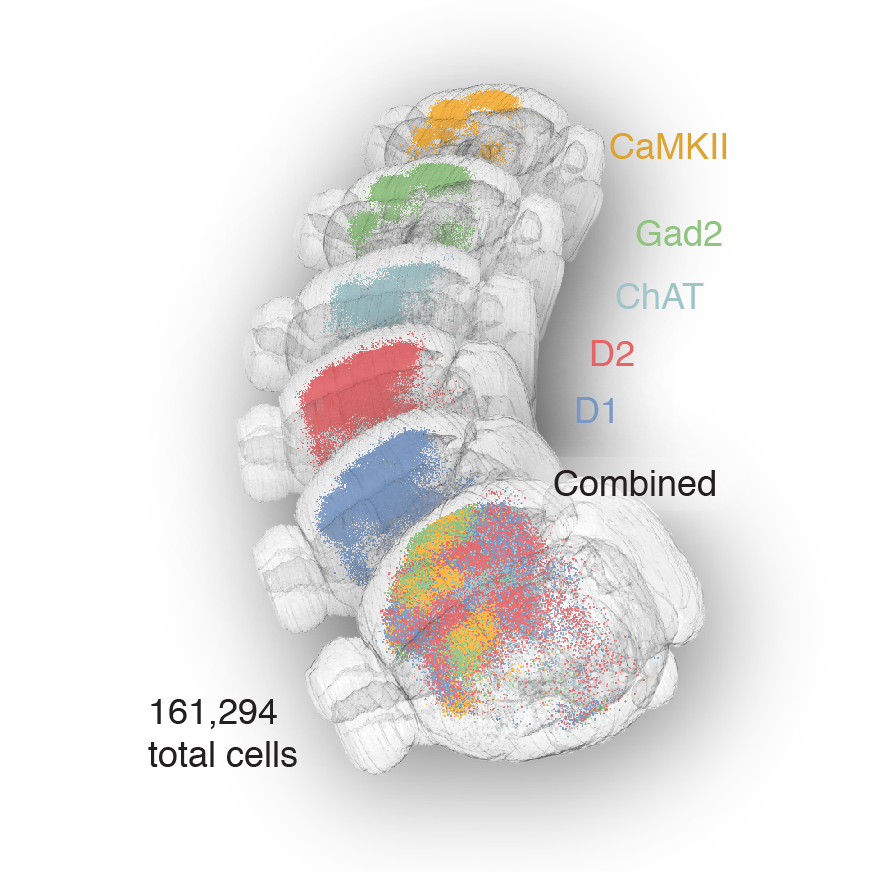
Tracing the network
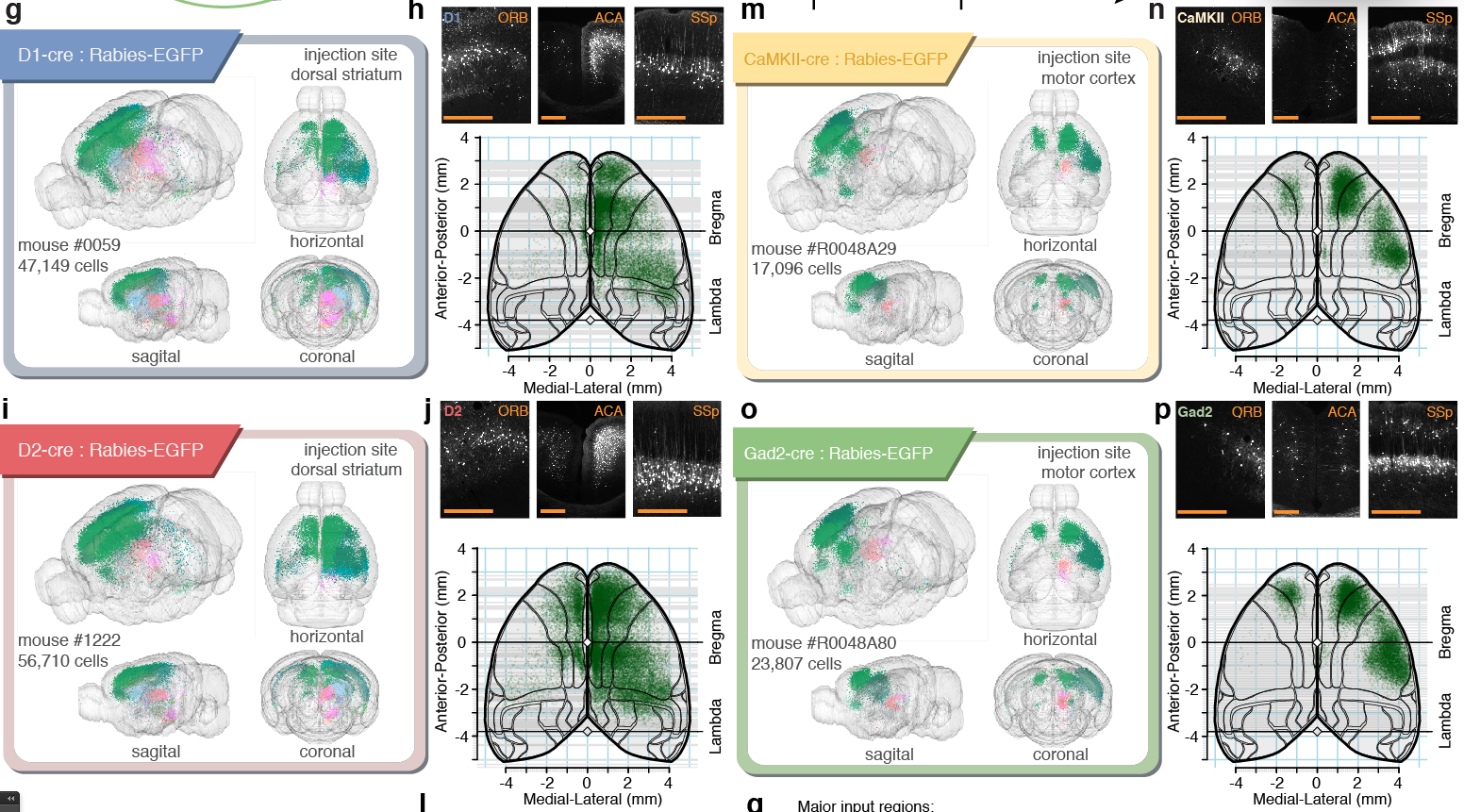
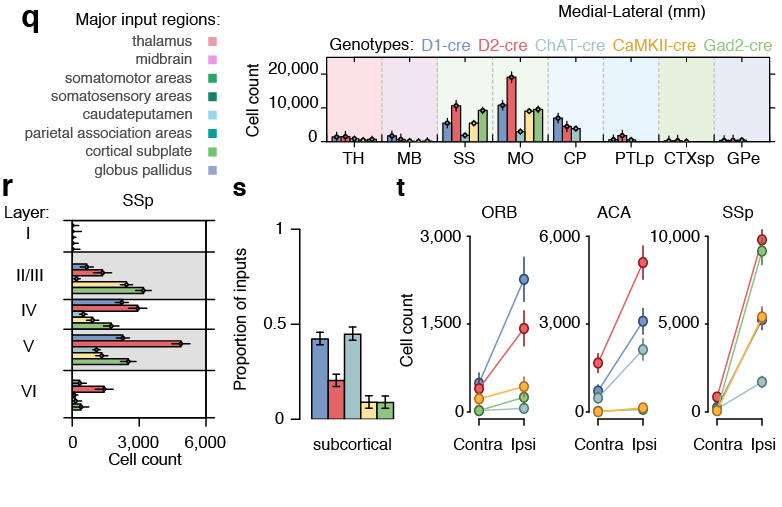
Tracing the network
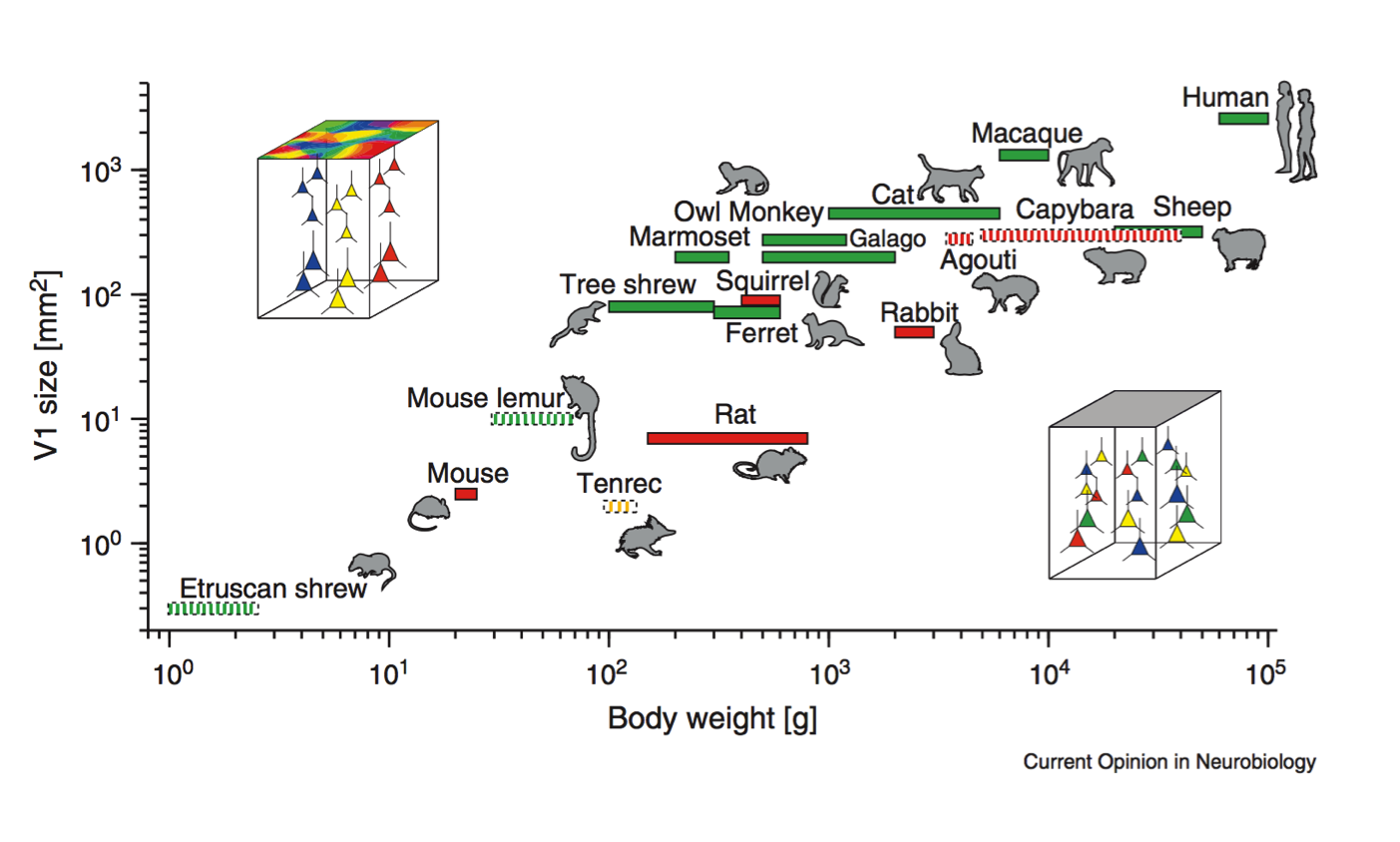
Scaling rules for rodent brians
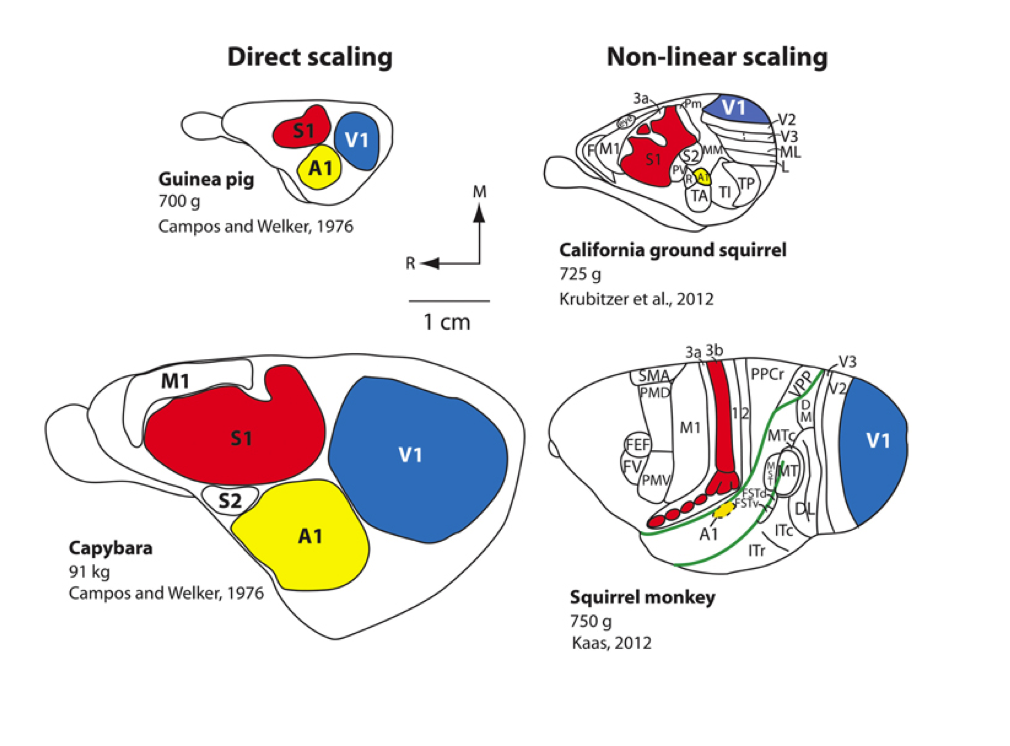
Isometric
Allometric
V \propto M^1
V∝M1
V \propto M^k, \quad k \neq 1
V∝Mk,k=1
Cellular scaling rules for rodent brians
Herculano-Houzel et al. PNAS
Cellular scaling rules
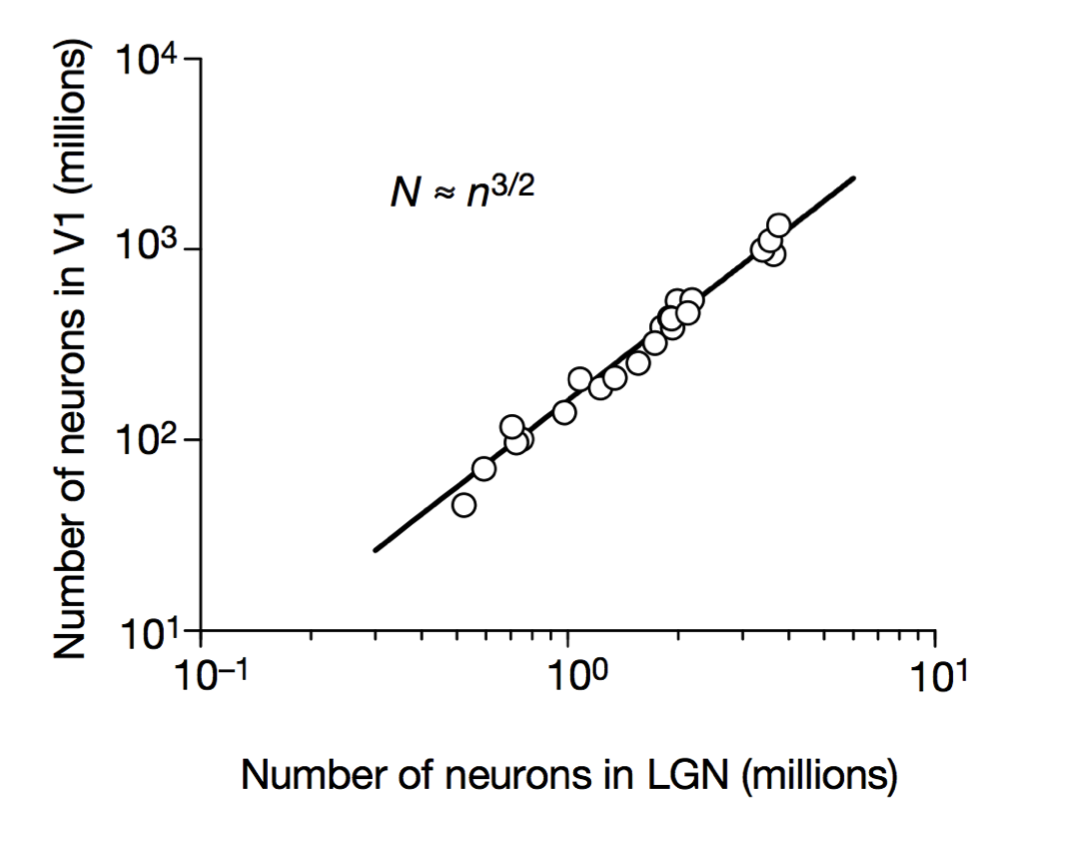
Stevens (2000) Nature
Cellular scaling rules
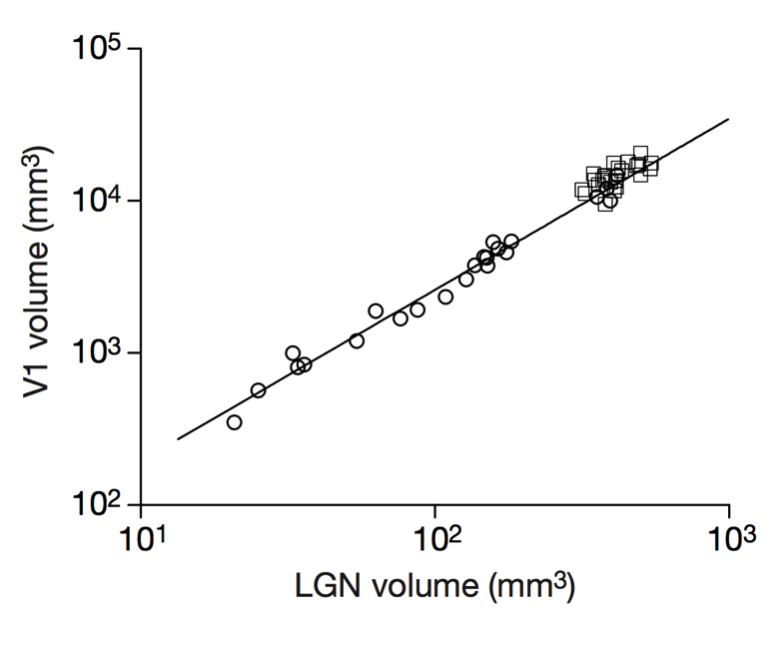
Stevens (2000) Nature
Cellular scaling rules
Hubel & Wiesel (1974), Blasdel (1986)
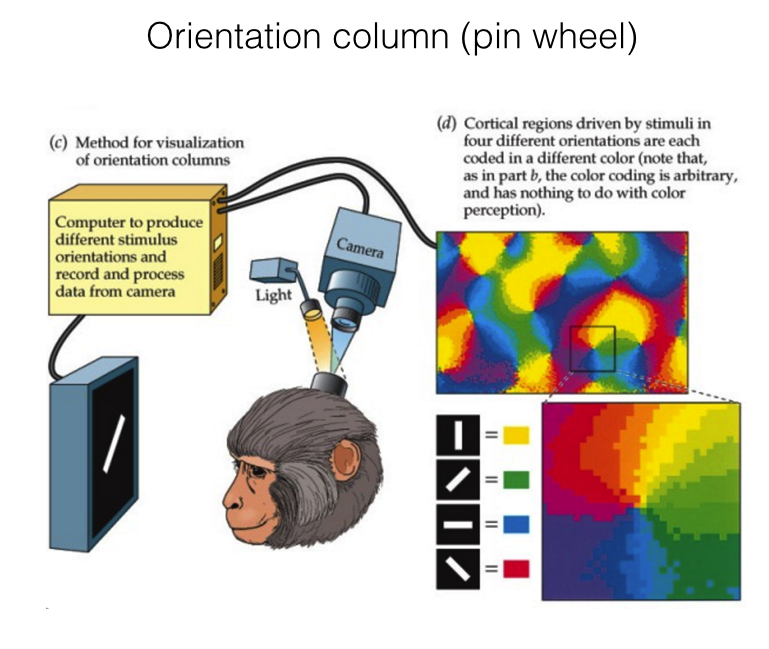
Cellular scaling rules
n
n
n^{1/2}
n1/2
n^{3/2}
n3/2
Cellular scaling rules
Stevens (2000) Nature
n \rightarrow n^{1/2} \rightarrow n^{3/2}
n→n1/2→n3/2
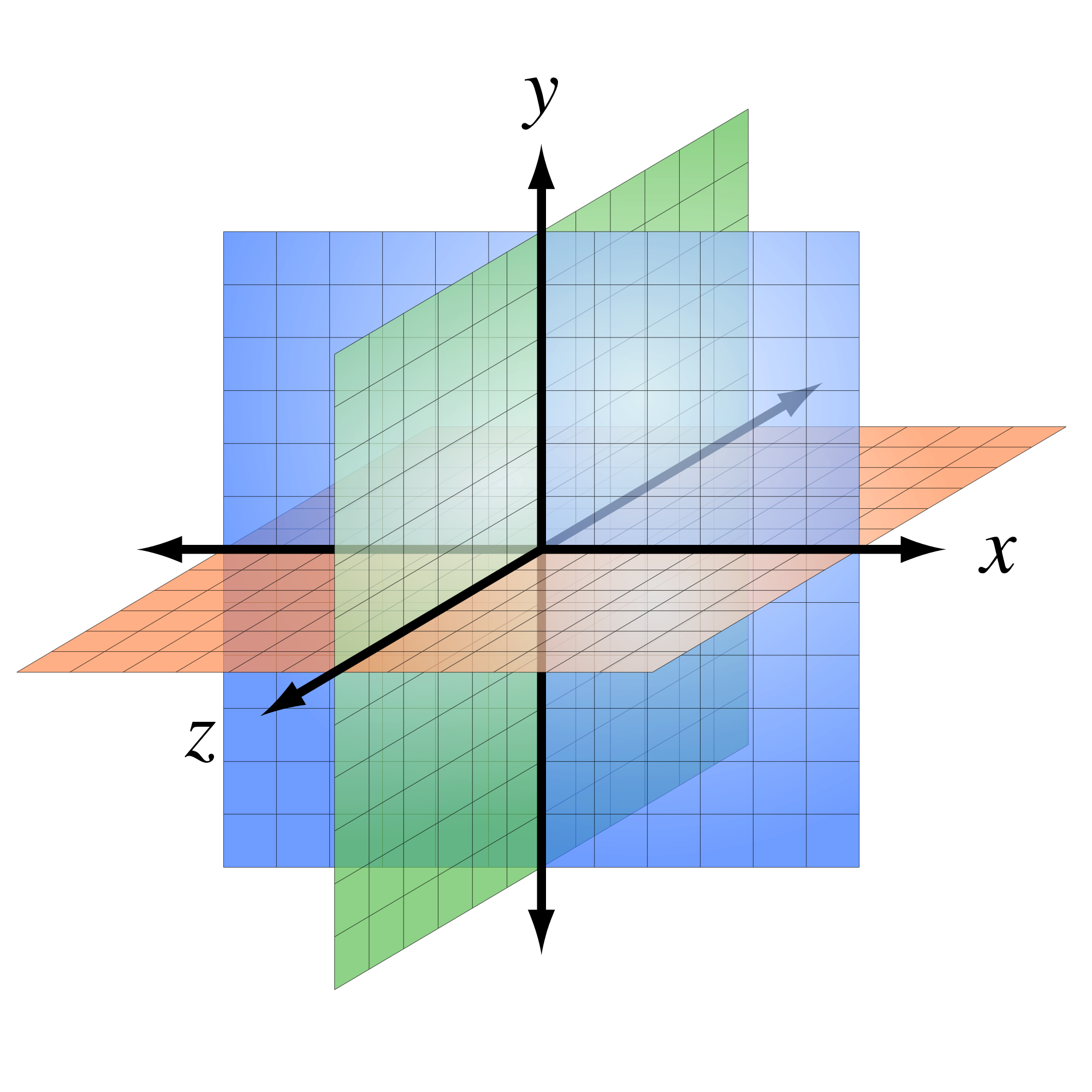
Cellular scaling rules
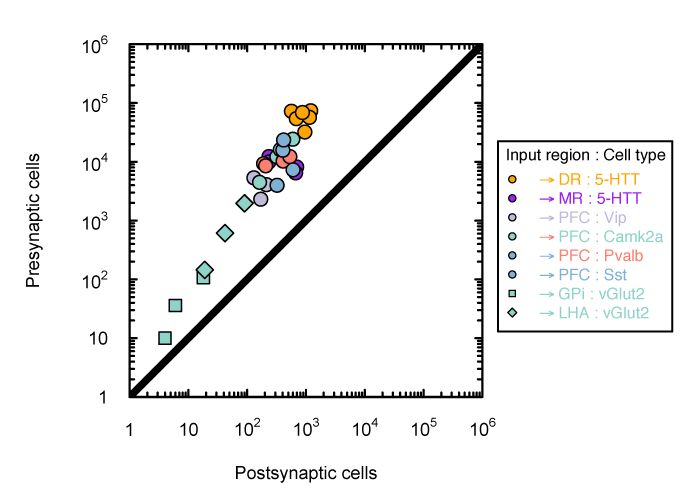
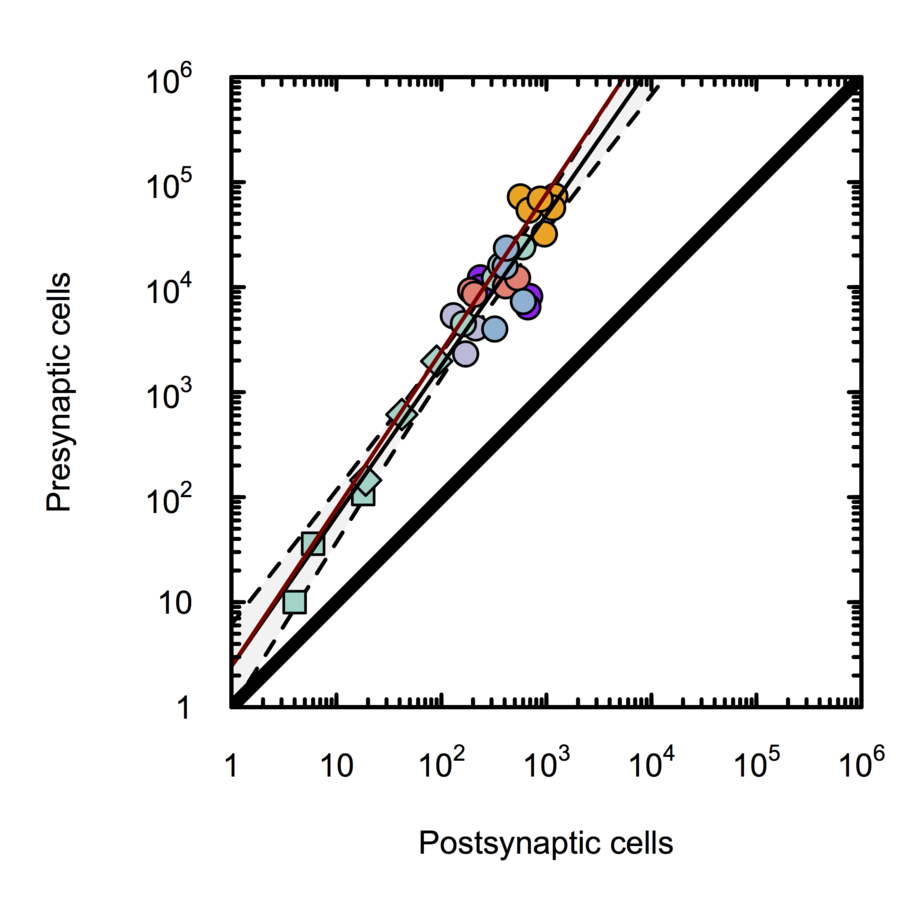
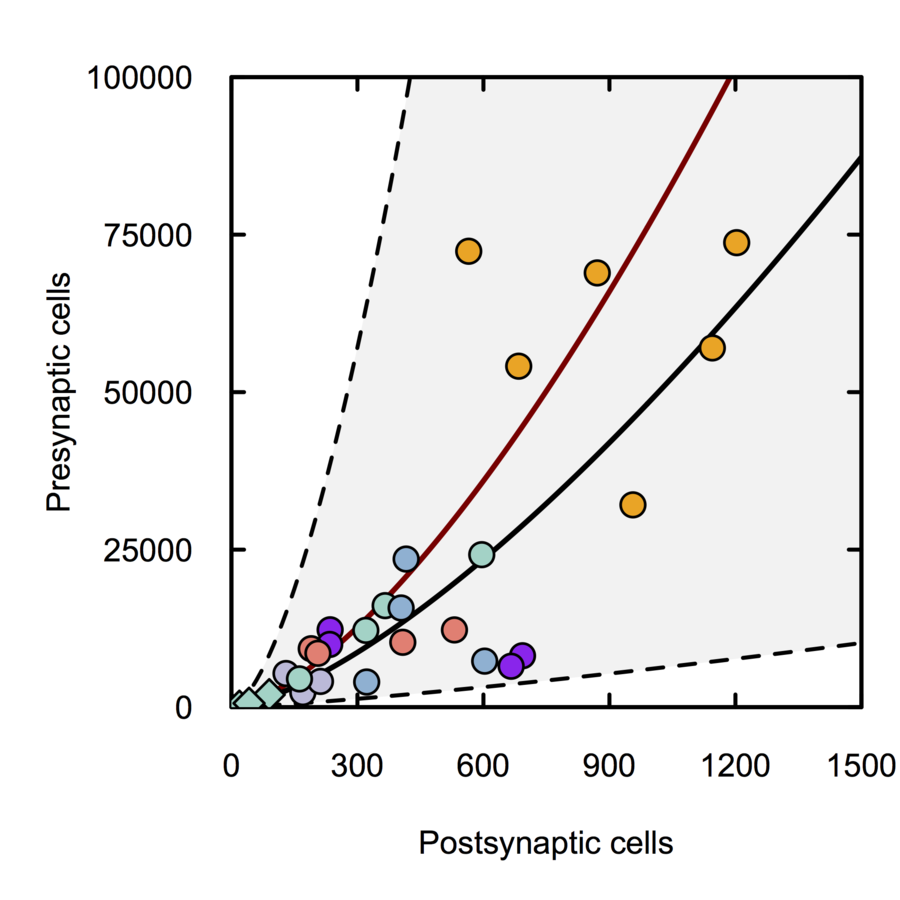
Monosynaptic scaling in mice
k = 1.44, \quad (95\% \text{C.I:} \quad 1.27 - 1.60)
k=1.44,(95%C.I:1.27−1.60)
Synapse density and dendritic branching
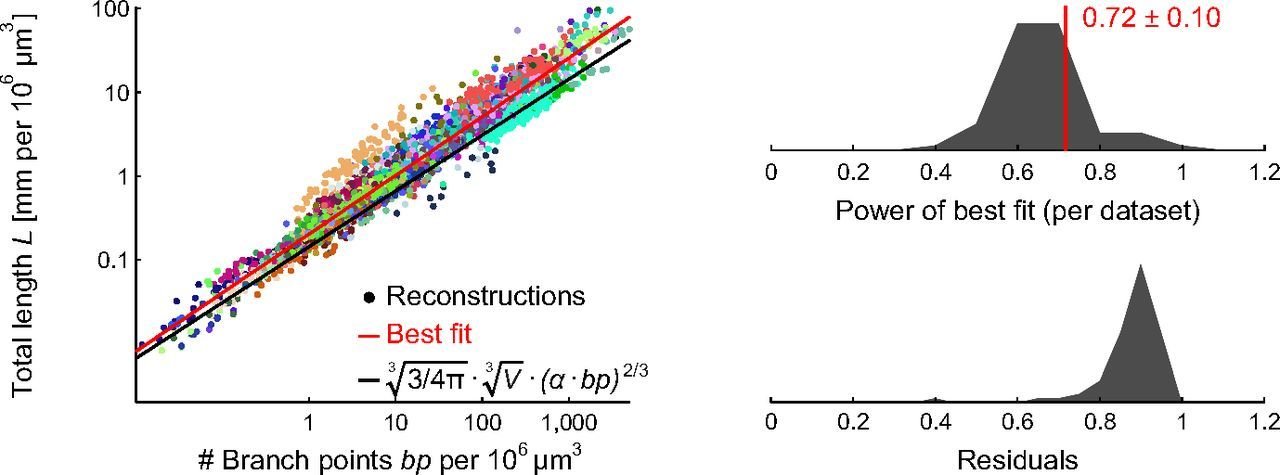
Cuntz, Mathy & Häusser (2012) PNAS
Synapse density and dendritic branching
Livneh, Feinstein, Klein and Mizrahi (2009) JoN
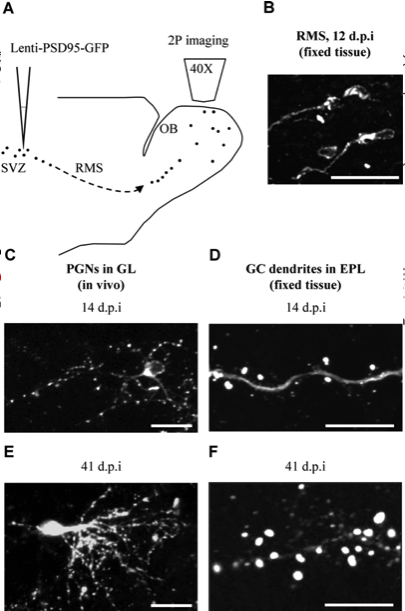
Synapse density and dendritic branching
Cuntz, Mathy & Häusser (2012) PNAS
Synapse density and dendritic branching
Cuntz, Mathy & Häusser (2012) PNAS
L \propto bp \propto puncta
L∝bp∝puncta
Self-organizing branching process
p(t+1) = p(t) + \frac{1-\sigma_i(p,t)}{N}
p(t+1)=p(t)+N1−σi(p,t)
P_i(s,p) = s^{-3/2} \sqrt{\frac{2(1-p)}{\pi p}} \exp\left( \frac{-s\ln(4p(1-p))}{-2} \right)
Pi(s,p)=s−3/2πp2(1−p)exp(−2−sln(4p(1−p)))
P_i(s) \propto s^{-3/2}
Pi(s)∝s−3/2
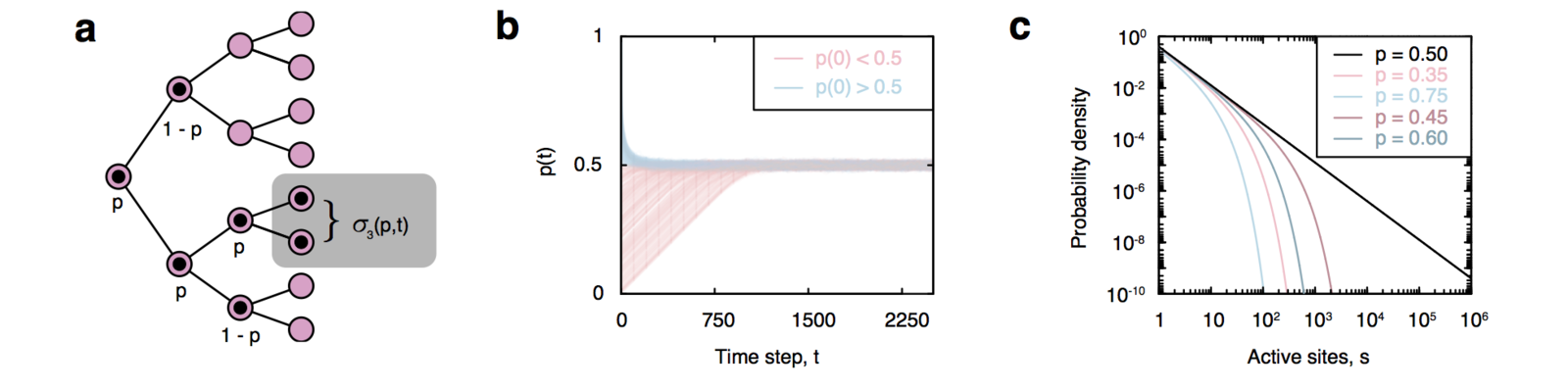
Self-organizing branching process
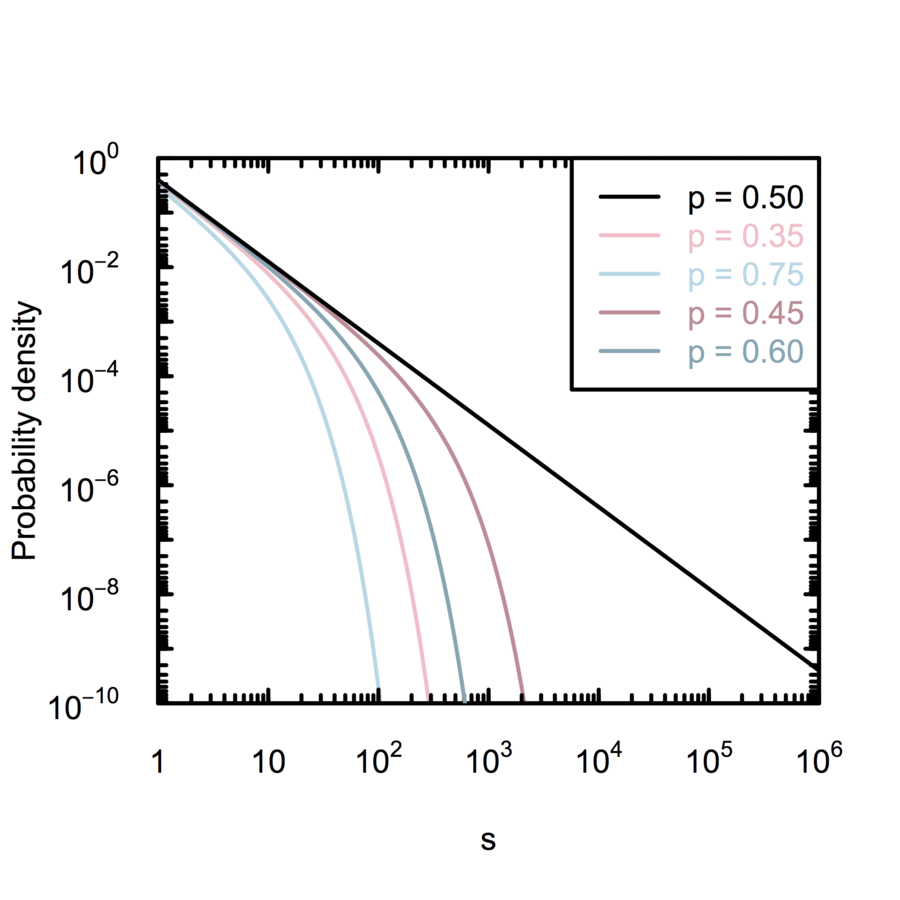
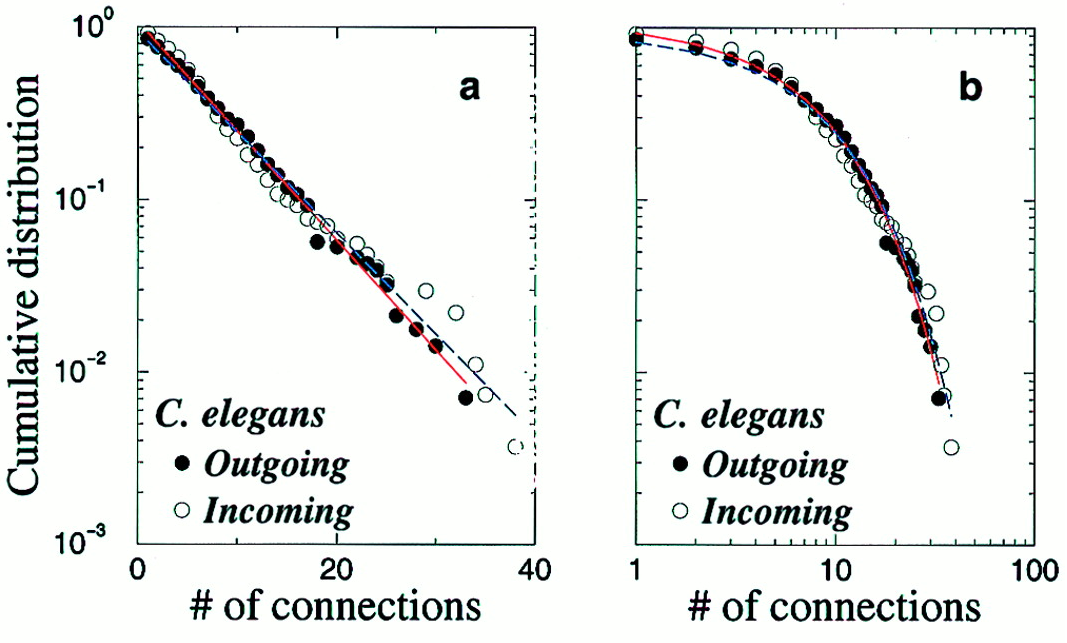
Amaral et al. (2000); White, Southgate, Thompson & Brenner (1986)
Mean-field results
Y = \sum\limits_{i;j;k} w_k F_{ij}^k,
Y=i;j;k∑wkFijk,
Total output for the network:
I_{ik} = \sum\limits_{j} F_{ij}^k,
Iik=j∑Fijk,
Total connection of type k for ith neuron:
\bar{I}_{ik} = p(k)s\frac{N_{\text{post}} - 1}{N_{\text{pre}}},
Iˉik=p(k)sNpreNpost−1,
Average number of connections in network
Mean-field results
Cost per unit length for dendrite to cover an area
Set average number of connections to the cost for the dendritic tree
\frac{p(k)s}{\epsilon} N_{\text{post}} = N_{\text{pre}}^{2/3},
ϵp(k)sNpost=Npre2/3,
C = \epsilon\sqrt{N_{\text{pre}}},
C=ϵNpre,
p(k)s\frac{N_{\text{post}}}{N_{\text{pre}}} = \epsilon\sqrt{N_{\text{pre}}},
p(k)sNpreNpost=ϵNpre,
\bar{I}_{ik} = C,
Iˉik=C,
N_{\text{pre}} \propto N_{\text{post}}^{3/2},
Npre∝Npost3/2,
Bayesian inference
BF_{01} = 4.7
BF01=4.7
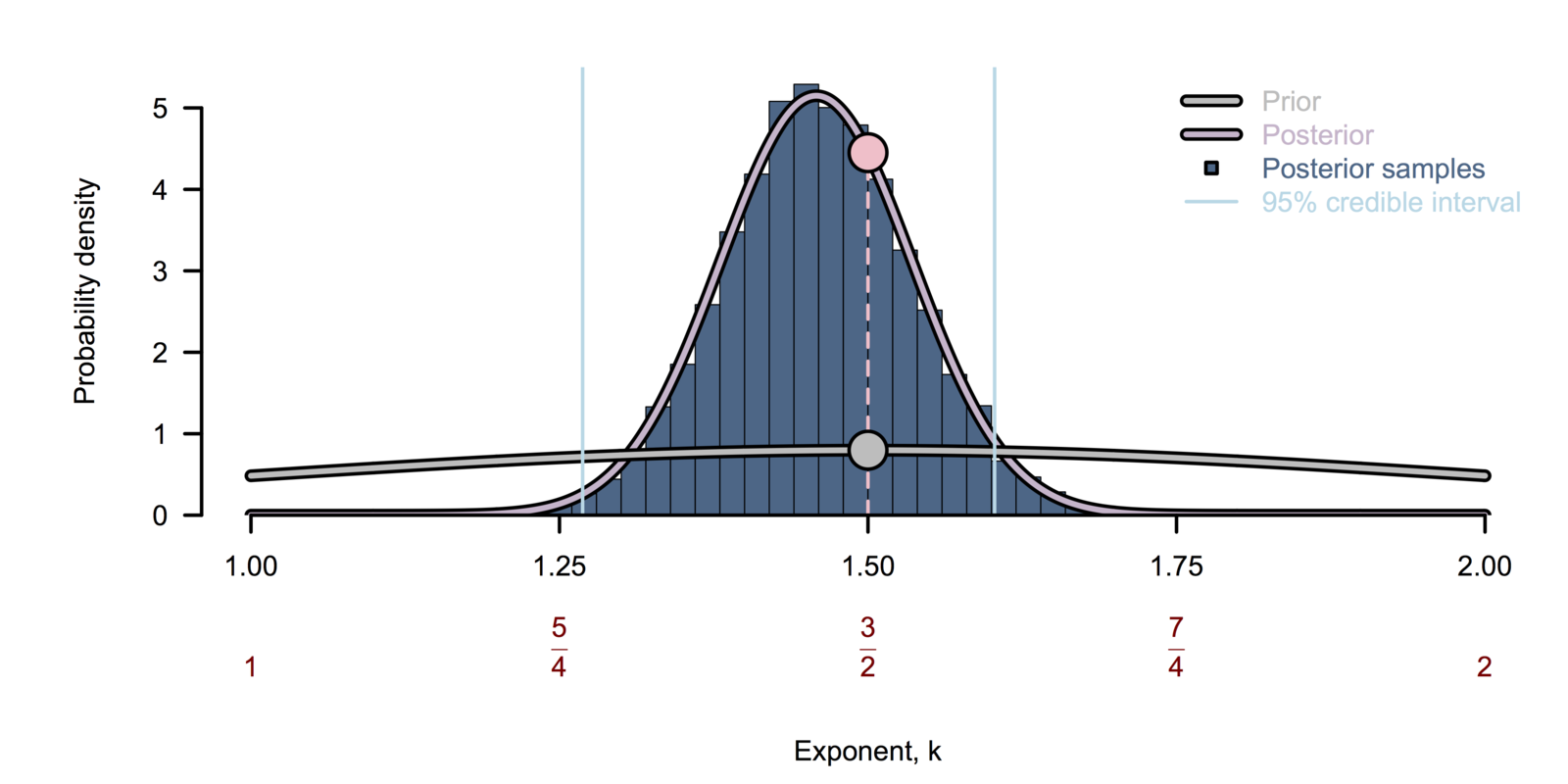
Bayesian inference
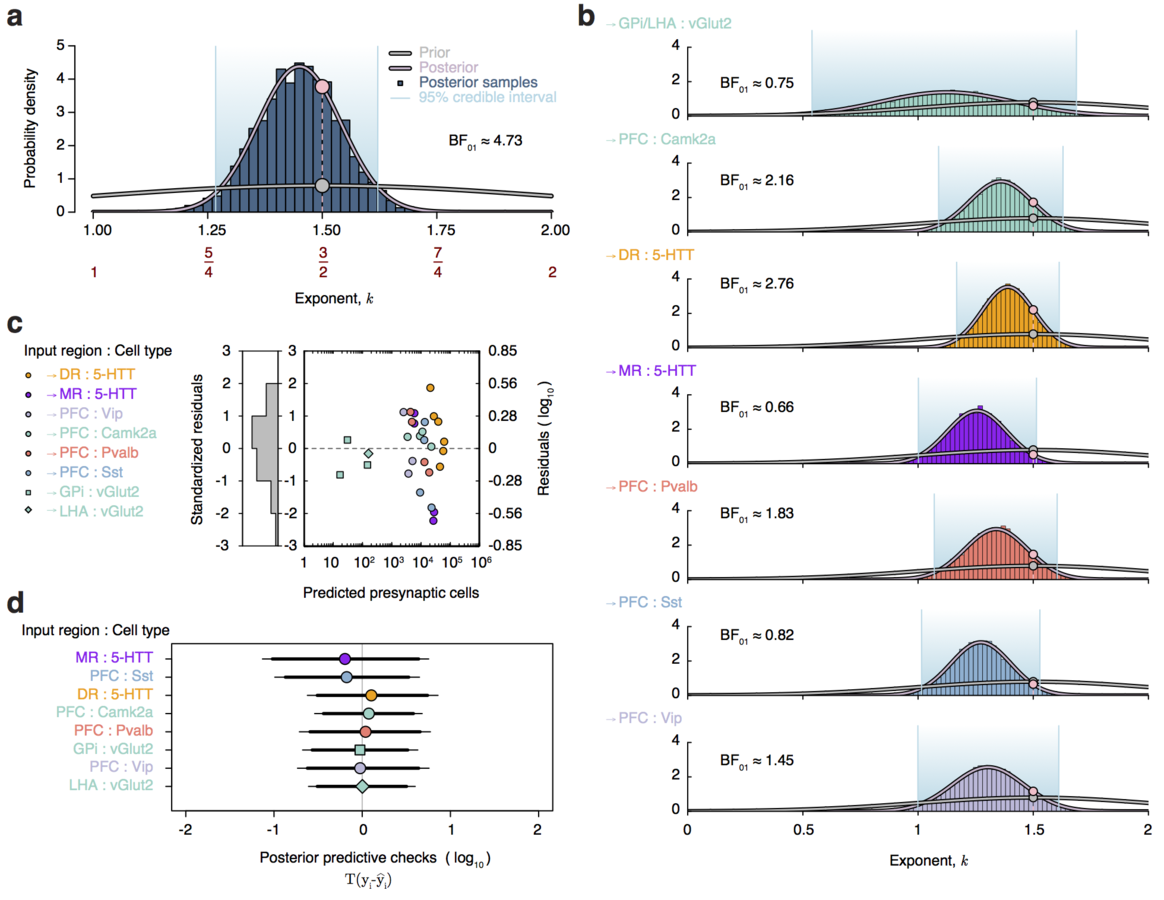
Dendritic pruning as an age-dependent branching process
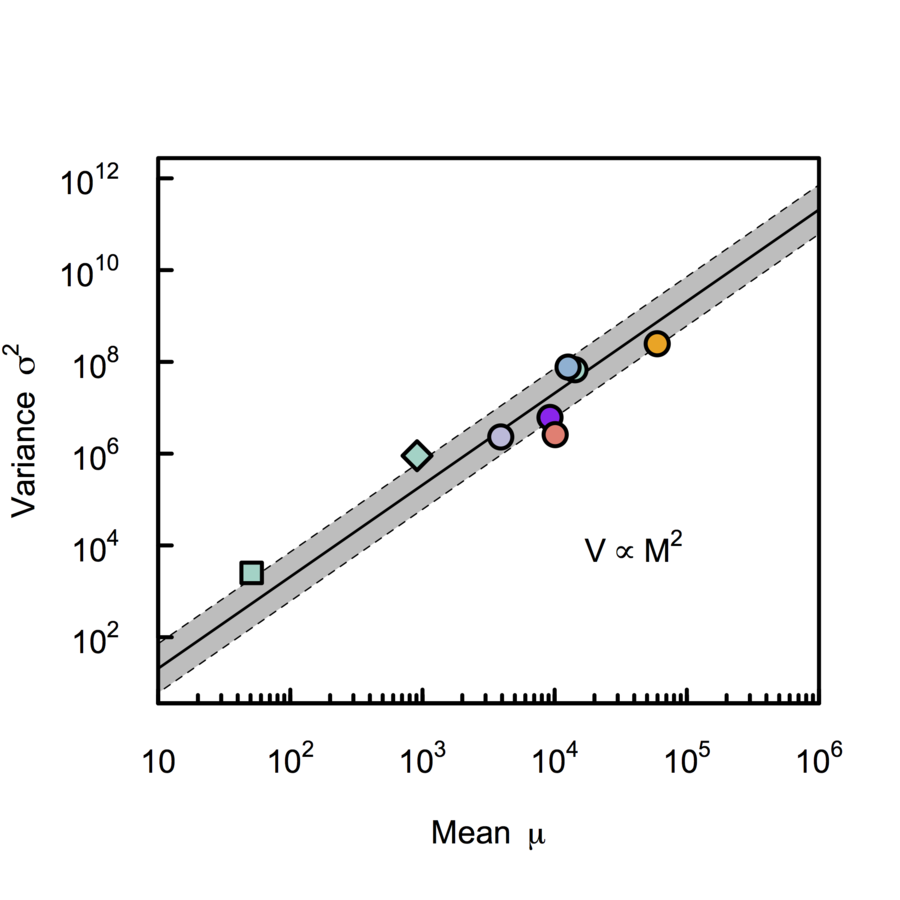
Cowan, (1984), Azevedo & Leroi (2000) PNAS
\mu = \theta \cdot e^{\alpha\cdot t}
μ=θ⋅eα⋅t
\sigma^2 = \lambda \theta^2 \cdot e^{2\alpha\cdot t} = \mu^2
σ2=λθ2⋅e2α⋅t=μ2
Data you shouldn't
go to war on
Data you do
go to war on
Thank you!
scRNA-seq
Gene specificity
about ~24'000 genes expressed in the brain.
\text{Let us define the following variables.}
Let us define the following variables.
c : \text{a unique single cell.} \quad \text{Where: } c \in \{1, ... , C\}, \text{ and } C = 380.
c:a unique single cell.Where: c∈{1,...,C}, and C=380.
m : \text{a unique single gene.} \quad \text{Where: } m \in \{1, ... , M\}, \text{ and } C = 380.
m:a unique single gene.Where: m∈{1,...,M}, and C=380.
D : \text{a } C \times D \text{ read count matrix.}
D:a C×D read count matrix.
D_{c,m} : \text{ normalized number of reads mapped to cell } c \text{ for gene } m.
Dc,m: normalized number of reads mapped to cell c for gene m.
r_{c,m} : \text{ cell-gene specificity ratio.}
rc,m: cell-gene specificity ratio.
r_{c,m} = \frac{D_{c,m}}{ s_m }
rc,m=smDc,m
s_{m} = \frac{1}{C} \sum_{i=1}^C D_{i,m}
sm=C1∑i=1CDi,m
s_{m} : \text{ gene specificity.}
sm: gene specificity.
Monosynaptic Scalable Architecture Revealed by Transsynaptic Rabies Tracing Daniel Fürth Meletis Lab Network for Networks 12 Feb 2016 daniel.furth@ki.se
Half-time2
By Daniel Fürth
Half-time2
- 465
