Active Inference with Semi-markov models
Dimitrije Marković
Theoretical Neurobiology Meeting
01.03.2020
Active inference and semi-markov decision processes
-
(Part I) Active inference in multi-armed bandits
- Empirical comparison with UCB and Thompson sampling.
- https://slides.com/dimarkov/ai-mbs
-
(Part II) Active inference and semi-Markov processes
- Hidden semi-Markov models and a representation of state duration.
- Learning the hidden temporal structure of state transitions.
- Application: Reversal learning task.
-
(Part III) Active inference and semi-Markov decision processes
- Extending policies with action (policy) duration.
- Decision about when actions should be taken and for how long.
- Applications: Temporal attention, intertemporal choices.
Active inference and semi-markov decision processes
-
(Part I) Active inference in multi-armed bandits
- Empirical comparison with UCB and Thompson sampling.
- https://slides.com/dimarkov/ai-mbs
-
(Part II) Active inference and semi-Markov processes
- Hidden semi-Markov models and a representation of state duration.
- Learning the hidden temporal structure of state transitions.
- Application: Reversal learning task.
-
(Part III) Active inference and semi-Markov decision processes
- Extending policies with action (policy) duration.
- Decision about when actions should be taken and for how long.
- Applications: Temporal attention, intertemporal choices.
-
(Part II) Active inference and semi-Markov processes
- Hidden semi-Markov models and a representation of state duration.
- Learning the hidden temporal structure of state transitions.
- Application: Reversal learning task.
Semi-Markov processes
https://en.wikipedia.org/wiki/Markov_renewal_process#Relation_to_other_stochastic_processes
- State space S
- Jump times \(T_n\) and states \( X_n\)
- Inter-arrival time \( \tau_n = T_n - T_{n-1}\)
- The sequence \( [(X_0, T_0), \ldots, (X_n, T_n), \ldots]\) is called a Markov renewal process if:
Pr\left(\tau_n \leq t, X_{n}=j| (X_0, T_0), \ldots, (X_{n-1}=i, T_n) \right) = Pr\left(\tau_n \leq t, X_{n}=j| X_{n-1}=i \right)
If \( Y_t \equiv X_n \) for \( t \in \left[T_n, T_{n+1} \right)\) then the process \(Y_t\) is called a semi-Markov process
Semi-Markov processes
State space \( S\)
X_0
X_1
X_2
X_{n-1}
X_n
X_{n+1}
\( \ldots\)
\( \ldots\)
T_0
T_1
T_2
T_{n-1}
T_{n}
T_{n+1}
Time
\tau_1
\tau_2
\tau_n
\tau_{n+1}
Special cases
For exponentially distributed iid waiting times we have a continuous time Markov chain
Pr\left(\tau_n \leq t, X_{n}=j| X_{n-1}=i \right) = Pr\left(X_{n}=j| X_{n-1}=i \right) \left( 1 - e^{\lambda_i t} \right)
A discrete time Markov chain has geometrically distributed waiting times
Pr\left(X_{n}=i| X_{n-1}=i \right) = p_i
\tau_n \sim p(\tau|p_i) = p_i^{\tau - 1}(1 - p_i), \:\: \tau \in \{1, 2, 3, \ldots\}
Hidden Semi-Markov models
Shun-Cheng Yu, "Hidden semi-Markov Models: Theory, Algorithms and Applications", Elsevir 2016.
A graphical representation of HSMM
Latent variables
outcomes
f_t
s_t
o_t
f_{t-1}
f_{t+1}
s_{t-1}
s_{t+1}
o_{t-1}
o_{t+1}
Example
\( f \in \{1, 2, 3\}\)
\tau = 3
time step
1
2
3
A
B
\( s \in \{A, B\}\)
\tau = 5
\tau = 2
p(f_t|f_{t-1}, s_{t-1}) \equiv \tau \sim p(\tau|s)
Example
\( f \in \{1, 2, 3\}\)
\tau = 3
time step
1
2
3
A
B
\( s \in \{A, B\}\)
\tau = 5
\tau = 2
p(f_t|f_{t-1}) \equiv \tau \sim p(\tau)
Phase transitions
\[p(f_t|f_{t-1})\]
M Varmazyar, et al., Journal of Industrial Engineering International (2019).
Discrete phase-type distribution
\omega_i = {n \choose i-1} (1 - \delta)^{n - i + 1}\delta^{i-1}, \:\: \omega_0 = 1 - \sum_{i=1}^{n} \omega_i
1-\delta
1-\delta
1-\delta
\delta
\delta
n
n+1
\(\ldots\)
\omega_1
\omega_2
\omega_{n}
\omega_{0}
1
2
Phase transitions
\[p(f_t|f_{t-1})\]
M Varmazyar, et al., Journal of Industrial Engineering International (2019).
Discrete phase-type distribution
Duration distribution
Negative binomial
\[p(\tau) = {\tau + n - 2 \choose \tau-1}(1-\delta)^{\tau-1}\delta^n\]
E[\tau]=\frac{n (1-\delta)}{\delta}+1 = \mu + 1
Var[\tau] = \mu + \frac{\mu^2}{n}
\omega_i = {n \choose i-1} (1 - \delta)^{n - i + 1}\delta^{i-1}, \:\: \omega_0 = 1 - \sum_{i=1}^{n} \omega_i
1-\delta
1-\delta
1-\delta
\delta
\delta
n
n+1
\(\ldots\)
\omega_1
\omega_2
\omega_{n}
\omega_{0}
1
2
Phase transitions
\[p(f_t|f_{t-1})\]
State transitions
State transitions
\( p(s_t|s_{t-1}, f_{t-1})\)
A
B
A
B
1-\delta
1-\delta
1-\delta
\delta
\delta
1
n
n+1
2
\(\ldots\)
\omega_1
\omega_2
\omega_{n}
\omega_{0}
negative binomial distribution
\delta_d = p(s_{t+d}=B|s_t=A)
Active Inference
p\left(o_t^l| s_t^1, \ldots, s_t^K\right) = Cat\left( A^l \right)
p\left(A^l\right) = Dir(a^l)
p\left(s_t^k| s_{t-1}^k, \pi, f_t \right) = Cat\left( B^{k, \pi}_f \right)
p(\pi) = s_{max}\left( -\gamma G \right), \quad P(o^l_t) = s_{max} \left( C^l \right)
p\left(f_t| f_{t-1}, m \right) = Cat\left( L^{m} \right)
p(m) = Cat(M), \quad m = (\mu, n)
\mu \in \{ \mu_{min}, \ldots, \mu_{max} \}, \: n \in \{1, \ldots, n_{max}\}
m
s^1_{t-1}
s^1_{t}
A^l
o_t
B^k
\pi
f_{t-1}
f_{t}
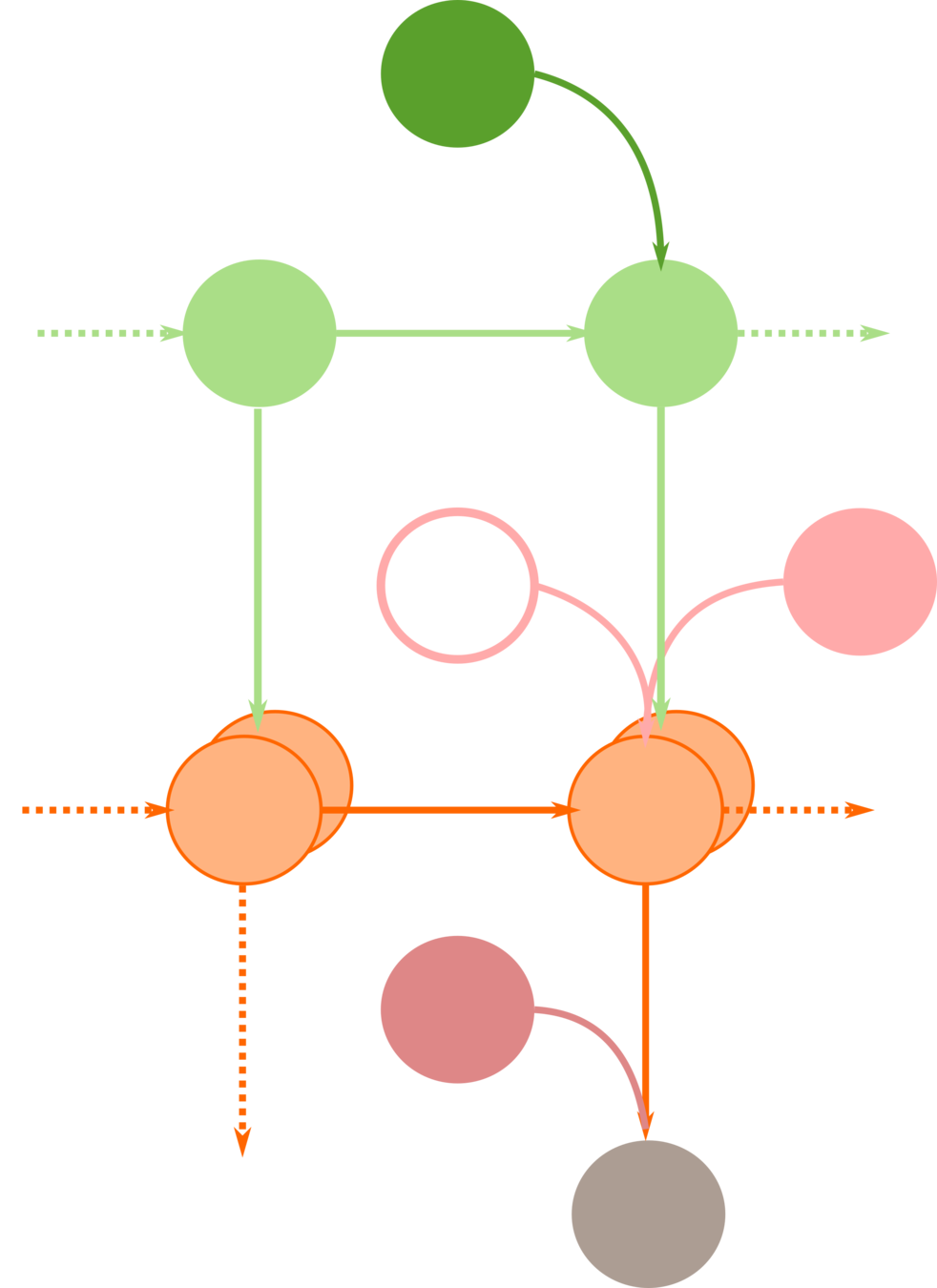
Belief updating and learning
History of past outcomes \( O_t = (o_1, \ldots, o_t) \)
Q(m) \propto p(o_t|m, O_{t-1}) p(m|O_{t-1})
Q(f_t|m) \propto p(o_t|f_t, O_{t-1}) p(f_t|m, O_{t-1})
Q(s_t|f_t) \propto p(o_t|s_t) e^{\sum_{\pi} Q(\pi) \ln p\left(s_t|f_t, \pi, O_{t-1} \right)}
Q(\pi) \propto p(o_t|\pi, O_{t-1}) p(\pi|O_{t-1})
Q(A) \propto e^{\sum_{s_t} Q(s_t) \ln p(o_t|s_t, A)} P(A|O_{t-1})
p(o_t| x, O_{t-1}) = \sum_y p(o_t|y) p(y|x, O_{t-1})
p(x_t|O_{t-1}) = \sum_{x_{t-1}} p(x_t|x_{t-1}) Q(x_{t-1})
Marginal likelihood
Predictive prior
Action selection
u_t \sim p\left(\pi|O_{t-1}\right) \propto e^{-\gamma G(\pi)}
When simulating behaviour \( \gamma \rightarrow \infty \)
For data analysis \( \gamma \) is a free parameter
G(\pi) = E_{Q(o_t|\pi)}\left[ \ln \frac{Q(o_t|\pi)}{P(o_t)} \right] - E_{Q(o_t, s_t, A|\pi)} \left[ \ln p(o_t|s_t, A) \right]
Probabilistic reversal learning
Probabilistic reversal learning
Probabilistic reversal learning
Model parameters
\( f \in \{1, \ldots, n_{max} \} \)
\( \otimes \)
\( \otimes \)
loss
gain
cue A
cue B
\(P(o_t^1) = [\frac{1}{3}, \frac{1}{3}, \frac{1}{3}] \)
\(P(o_t^2) = [\rho_1, \rho_2, \frac{\rho}{2}, \frac{\rho}{2}] \)
Performance
\frac{MA(t)}{1 - MA(t)}
Trials Until correct (TUC)
In SILICO
Is the experimental setup useful?
- Can the temporal structure be learned?
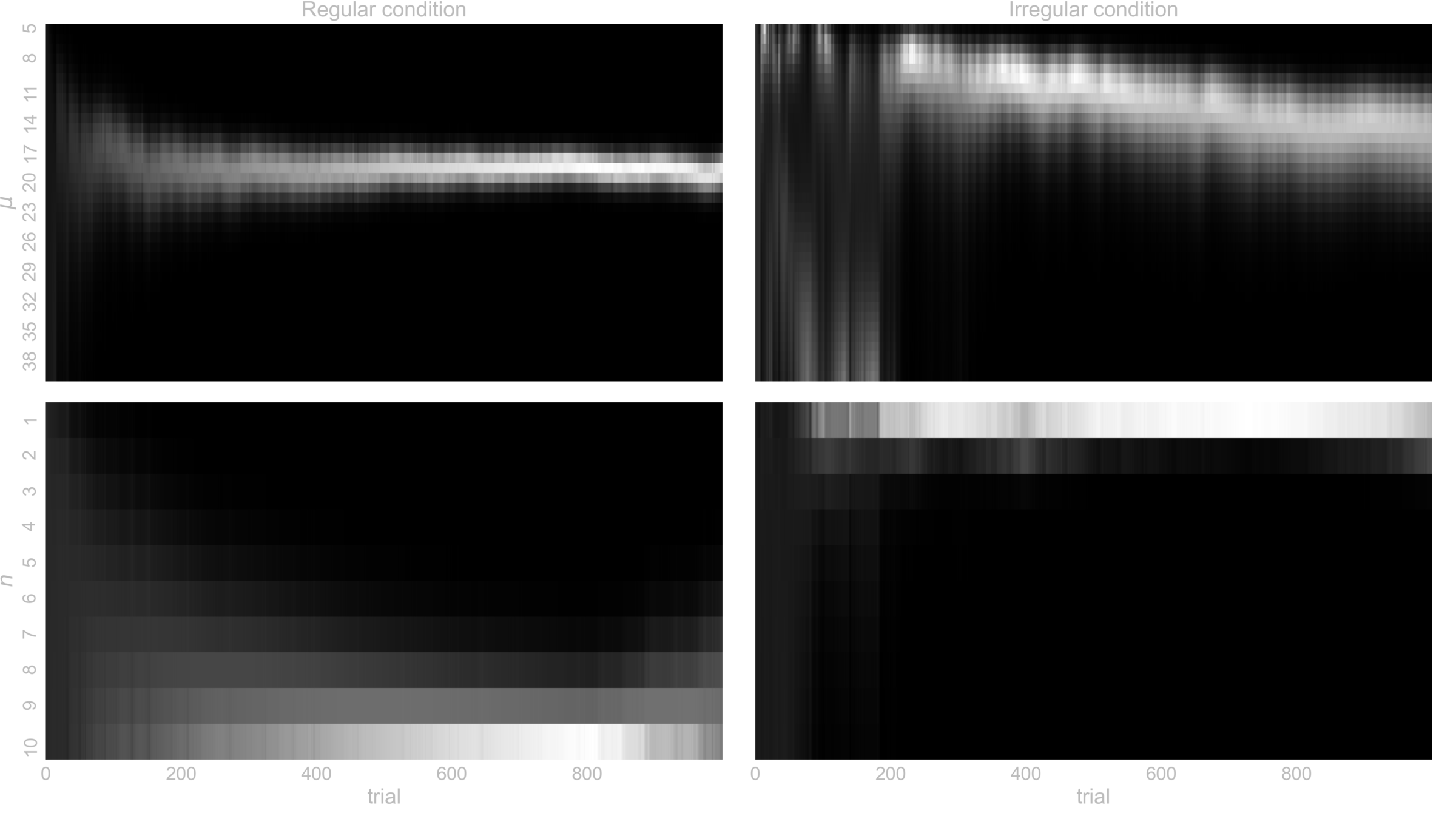
- Will different temporal beliefs reflect different behaviour?
- How well can we differentiate between agents with different temporal beliefs?
In SILICO
Process:
- Fix priors, and action precision \(\gamma\)
- Simulate behaviour in both conditions with different \(n_{max}\)
- Illustrate, performance, TUC, and the learning of the latent temporal structure \( (\mu, n) \)
- Model inversion, and confusion matrix for \(n_{max}\)
In SILICO - Behavioural metrics
In SILICO - Learning latent temporal structure
n_{max} = 10
In SILICO - Confusion matrix
In SILICO - Confusion matrix
Behavioural data
- 50 healthy volunteers (20-30 years old):
- 27 subjects in the condition with regular reversals
- 23 subjects in the condition with irregular reversals
- 40 trials long training with a single reversal
Performance-tuc trajectories
Model comparison
Labeled trajectories
conclusion
- Modelling and assessing influence of temporal-expectations on decision-making in dynamic environments.
- How people learn temporal expectations could also be addressed with this approach, but some challenges remain.
- Linking the underlying representation of the temporal structure to behaviour provides a novel method for computational cognitive phenotyping.
Thanks to:
- Andrea Reiter
- Stefan Kiebel
- Thomas Parr
- Karl Friston
https://slides.com/dimarkov/active-inference-semi-markov
https://github.com/dimarkov/pybefit
https://journals.plos.org/ploscompbiol/article?rev=2&id=10.1371/journal.pcbi.1006707
Active inference with semi-Markov models
By dimarkov
