Bayesian model reduction for nonlinear regression
Dimitrije Marković
DySCO meeting 18.01.2023
Outline
- Bayesian deep learning
- Structured shrinkage priors
- Bayesian model reduction
- Regression
- Non-linear regression
Outline
- Bayesian deep learning
- Structured shrinkage priors
- Bayesian model reduction
- Regression
- Non-linear regression
Deep learning
\pmb{h}^n_0 = \pmb{x}^n \\
\vdots \\
\pmb{h}^n_i = \pmb{f}(\pmb{h}^n_{i-1}, \pmb{W}_{i}) \\
\vdots \\
\pmb{h}^n_L = \pmb{f}(\pmb{h}^n_{L-1}, \pmb{W}_{L}) \\
\pmb{y}^n \sim p(y|\pmb{W}, \pmb{x}^n) = p(y|\pmb{h}_L^n)
\pmb{W}^* = \argmin_{\pmb{W}} \sum_{n=1}^N \ln p(\pmb{y}^n|\pmb{W}, \pmb{x}^n)
Optimization
Bayesian deep learning
\pmb{h}^n_0 = \pmb{x}^n \\
\vdots \\
\pmb{h}^n_i = \pmb{f}(\pmb{h}^n_{i-1}, \pmb{W}_{i}) \\
\vdots \\
\pmb{h}^n_L = \pmb{f}(\pmb{h}^n_{L-1}, \pmb{W}_{L}) \\
\pmb{y}^n \sim p(y|\pmb{W}, \pmb{x}^n) = p(y|\pmb{h}_L^n)
p\left( \pmb{W} |\pmb{\mathcal{D}}\right)\propto p(\pmb{W}) \prod_{n=1}^N p(\pmb{y}^n|\pmb{W}, \pmb{x}^n)
Inference
Advantages
- More robust, accurate and calibrated predictions
- Learning from small datasets
- Continuous learning (inference)
- Distributed or federated learning (inference)
- Marginalization
p\left(\pmb{Y}_{test}|\pmb{X}_{test} \right) = \int d \pmb{W} p\left(\pmb{Y}_{test}| \pmb{W}, \pmb{X}_{test} \right) p\left(\pmb{W}|\mathcal{D}_{train}\right)
Few references
Murphy, Kevin P. Probabilistic machine learning: an introduction. MIT press, 2022.
Wilson, Andrew Gordon. "The case for Bayesian deep learning." arXiv preprint arXiv:2001.10995 (2020).
Bui, Thang D., et al. "Partitioned variational inference: A unified framework encompassing federated and continual learning." arXiv preprint arXiv:1811.11206 (2018).
Murphy, Kevin P. Probabilistic machine learning: Advanced Topics. MIT Press 2023
Outline
- Bayesian deep learning
- Structured shrinkage priors
- Bayesian model reduction
- Regression
- Non-linear regression
Deep learning
\pmb{h}^n_0 = \pmb{x}^n \\
\vdots \\
\pmb{h}^n_i = \pmb{f}(\pmb{h}^n_{i-1}, \pmb{W}_{i}) \\
\vdots \\
\pmb{h}^n_L = \pmb{f}(\pmb{h}^n_{L-1}, \pmb{W}_{L}) \\
\pmb{y}^n \sim p(y|\pmb{W}, \pmb{x}^n) = p(y|\pmb{h}_L^n)
\pmb{W}^* = \argmin_{\pmb{W}} \sum_{n=1}^N \ln p(\pmb{y}^n|\pmb{W}, \pmb{x}^n)
Optimization
Structured shrinkage priors
Nalisnick, Eric, José Miguel Hernández-Lobato, and Padhraic Smyth. "Dropout as a structured shrinkage prior." International Conference on Machine Learning. PMLR, 2019.
Ghosh, Soumya, Jiayu Yao, and Finale Doshi-Velez. "Structured variational learning of Bayesian neural networks with horseshoe priors." International Conference on Machine Learning. PMLR, 2018.
Dropout as a spike-and-slab prior
p(w_{lij}) \propto \pi_l \mathcal{N}(0, \sigma_0^2) + (1-\pi_l) \delta(w)
Better shrinkage priors
p(w_{lij}) = \pi \mathcal{N}(0, \sigma_0^2 \tau_i^2 \lambda_{ij}^2), \: \lambda_{ij} \sim p(\lambda|\tau_i), \: \tau_i \sim p(\tau)
Regularized horseshoe prior
Piironen, Juho, and Aki Vehtari. "Sparsity information and regularization in the horseshoe and other shrinkage priors." Electronic Journal of Statistics 11.2 (2017): 5018-5051.
c_l^{-2} \sim \Gamma(2, 3) \\
\tau_{li} \sim C^+(0, \tau_0^2) \\
\lambda_{lij} \sim C^+(0, \tau_{li}) \\
\gamma_{lij}^2 = \frac{c_l^2 \lambda_{lij}^2}{c_l^2 + \lambda_{lij}^2}\\
w_{lij} \sim \mathcal{N} \left(0, \gamma_{lij}^2 \right)
\pmb{W} = (\pmb{W}_1, \ldots, \pmb{W}_L) \\
\pmb{W}_l = \left[ w_{lij} \right]_{1 \leq i \leq D_{l}, 1 \leq j \leq D_{l-1}}
Outline
- Bayesian deep learning
- Structured shrinkage priors
- Bayesian model reduction
- Regression
- Non-linear regression
Factorization
q(\pmb{z}|\pmb{\phi}) = q(\pmb{z}_K)\prod_{i=1}^{K-1} q(\pmb{z}_i|\pmb{z}_{i+1})\quad (1) \\
q(\pmb{z}|\pmb{\phi}) = q(\pmb{z}_1)\prod_{i=2}^K q(\pmb{z}_i|\pmb{z}_{i-1})\quad (2) \\
q(\pmb{z}|\pmb{\phi}) = \prod_{i=1}^K q(\pmb{z}_i)\quad (3) \\
Approximate posterior
p(\pmb{z}|\pmb{\mathcal{D}})\propto p(\pmb{z}_K) p(\mathcal{D}|\pmb{z}_1) \prod_{i=1}^{K-1} p(\pmb{z}_i|\pmb{z}_{i+1})
Hierarchical model
Non-centered parameterization
Approximate posterior
p(\pmb{\tilde{z}}|\pmb{\mathcal{D}})\propto p(\mathcal{D}|\pmb{\tilde{z}}_1, \ldots, \pmb{\tilde{z}}_K) \prod_{i=1}^{K} p(\pmb{\tilde{z}}_i)
Hierarchical model
q\left(\pmb{\tilde{z}}|\pmb{\tilde{\phi}}\right) = \prod_{i=1}^K q(\pmb{\tilde{z}}_i|\tilde{\pmb{\phi}}_i)
F = \sum_{i=1}^K F[\pmb{\tilde{\phi}}_i] \\
F\left[ \pmb{\tilde{\phi}}_i\right] = E_{q(\pmb{\tilde{z}}_i)}\left[ f(\pmb{\tilde{z}}_i) + \ln q(\pmb{\tilde{z}}_i) \right]\\
f(\pmb{\tilde{z}}_i) = - \frac{1}{K} \int \frac{q(\pmb{\tilde{z}})}{q(\pmb{\tilde{z}}_i)} \ln p(\pmb{\tilde{z}}_i)^Kp(D|\pmb{\tilde{z}}) \prod_{j\neq i} d \pmb{\tilde{z}}_j
Variational free energy
Stochastic variational inference
Stochastic gradient
F = \sum_i F\left[ \pmb{\tilde{\phi}}_i\right] \rightarrow \dot{\pmb{\tilde{\phi}}}_i = - \nabla_{\pmb{\tilde{\phi}}_i} F\left[ \pmb{\tilde{\phi}}_i\right]
\hat{f}(\pmb{\tilde{z}}_i) = - \frac{1}{S\cdot K}\sum_{s} \ln p(\pmb{\tilde{z}}_i)^K p(D^n|\pmb{\tilde{z}}^s, \pmb{\tilde{z}}_i)
\mathcal{D}^n \sub D, \qquad \pmb{\tilde{z}}^s \sim q(\pmb{\tilde{z}})
\nabla_{\pmb{\tilde{\phi}}_i} \hat{F}\left[ \pmb{\tilde{\phi}}_i\right] = \frac{1}{S} \sum_s \left[ \nabla_{\pmb{\tilde{z}}_i} \hat{f}(\pmb{\tilde{z}}_i) \nabla_{\pmb{\tilde{\phi}}_i} \pmb{\tilde{z}}_i |_{\pmb{\tilde{z}}_i = \pmb{\tilde{z}}_i^s} + \ln q(\pmb{\tilde{z}}_i^s) \nabla_{\pmb{\tilde{\phi}}_i} q(\pmb{\tilde{z}}_i^s) \right]
\nabla_{\pmb{\tilde{\phi}}_i} F\left[ \pmb{\tilde{\phi}}_i\right] = E_{q(\pmb{\tilde{z}}_i)}\left[ \nabla_{\pmb{\tilde{z}}_i} f(\pmb{\tilde{z}}_i) \nabla_{\pmb{\tilde{\phi}}_i} \pmb{\tilde{z}}_i + \ln q(\pmb{\tilde{z}}_i) \nabla_{\pmb{\tilde{\phi}}_i} \ln q(\pmb{\tilde{z}}_i) \right]\\
Bayesian model reduction
Two generative processes for the data
p\left( \pmb{z}|\mathcal{D} \right) \propto p\left( \mathcal{D}| \pmb{z}\right) p\left( \pmb{z} \right)
flat model
\tilde{p}\left( \pmb{z}|\mathcal{D} \right) \propto p\left( \mathcal{D}| \pmb{z}\right) \tilde{p}\left( \pmb{z} \right)
extended model
-\ln \tilde{p}(\mathcal{D}) = - \ln p(\mathcal{D}) - \ln \int d \pmb{z} p(\pmb{z}|\mathcal{D})
\frac{\tilde{p}(\pmb{z})}{p(\pmb{z})}
-\ln \tilde{p}(\mathcal{D}) \approx F\left[ \pmb{\phi}^* \right] - \ln \int d \pmb{z} q\left(\pmb{z}| \pmb{\phi}^* \right)
\frac{\tilde{p}(\pmb{z})}{p(\pmb{z})}
Friston, Karl, Thomas Parr, and Peter Zeidman. "Bayesian model reduction." arXiv preprint arXiv:1805.07092 (2018).
Bayesian model reduction
p\left( \pmb{z}_{i-1}|\mathcal{D} \right) \propto p\left( \mathcal{D}| \pmb{z}_{i-1} \right) p\left( \pmb{z}_{i-1} \right)
flat model
p\left( \pmb{z}_{i-1}|\mathcal{D}, \pmb{z}_{i} \right) \propto p\left( \mathcal{D}| \pmb{z}_{i-1} \right) p\left( \pmb{z}_{i-1}|\pmb{z}_{i} \right)
extended model
F\left[ \pmb{\phi}_{i} \right] = \int d \pmb{z}_i q(\pmb{z}_i) \ln \frac{q(\pmb{z}_i)}{p(\mathcal{D}|\pmb{z}_i)p(\pmb{z}_i)}
\approx \int d \pmb{z}_i q(\pmb{z}_i) \left[ - \ln E_{q^*(\pmb{z}_{i-1})}\left[ \frac{p(\pmb{z}_{i-1}|\pmb{z}_i)}{p(\pmb{z}_{i-1})} \right] + \ln \frac{q(\pmb{z}_i)}{p(\pmb{z}_i)}\right] \equiv \tilde{F}[\pmb{\phi}_i]
BMR algorithm
p\left( \pmb{z}_{i}|\mathcal{D} \right) \propto p\left( \mathcal{D}| \pmb{z}_{i} \right) p\left( \pmb{z}_{i} \right)
p\left( \pmb{z}_{i}|\mathcal{D}, \pmb{z}_{i+1} \right) \approx q\left( \pmb{z}_{i}| \pmb{z}_{i+1} \right)
\ln q(\pmb{z}_{i}|\pmb{z}_{i+1}) = \ln q^*(\pmb{z}_{i}) + \ln \frac{p(\pmb{z}_{i}|\pmb{z}_{i+1})}{p(\pmb{z}_{i})} - \ln E_{q^*}\left[\frac{p(\pmb{z}_i|\pmb{z}_{i+1})}{p(\pmb{z}_i)} \right]
\pmb{\phi}_i^* = \argmin_{\pmb{\phi}_i} \tilde{F}[\pmb{\phi}_i]
Step 1
BMR algorithm
p\left( \pmb{z}_{i+1}|\mathcal{D} \right) \propto p\left( \mathcal{D}| \pmb{z}_{i+1} \right) p\left( \pmb{z}_{i+1} \right)
\bar{q}(\pmb{z}_{i}) = \int d\pmb{z}_{i+1} q(\pmb{z}_{i}|\pmb{z}_{i+1}) q(\pmb{z}_{i+1})
\pmb{\phi}_{i+1}^* = \argmin_{\pmb{\phi}_{i+1}} \tilde{F}[\pmb{\phi}_{i+1}]
Step 2
New epoch
\( p(\pmb{z}_i) \propto \exp\left[ \int d \pmb{z}_{i+1} p_{i|i+1}q_{i+1} \right] \)
step 1
\(\vdots\)
step 2
Outline
- Bayesian deep learning
- Structured shrinkage priors
- Bayesian model reduction
- Regression
- Non-linear regression
\pmb{x}_n \sim \mathcal{N}_D \left(0, \pmb{I} \right) \\
y_n \sim p\left( y| \pmb{W} \cdot \pmb{x}_n \right) \\
w_1 = 1, w_{d>1} = 0
Regression
Linear (D=(1,100), N=100)
\mathcal{N}\left(y; \pmb{W} \cdot \pmb{x}_n, \sigma^2 \right)
Logistic (D=(1,100), N=200)
\mathcal{Be}\left(y|s(\pmb{W} \cdot \pmb{x}_n)\right)
Multinomial (D=(10,10), N=400)
\mathcal{Cat}\left(y|\rho(\pmb{W} \cdot \pmb{x}_n)\right)
Generative model
p(\tau)p(\pmb{\lambda}|\tau) p(\pmb{W}|\lambda) \prod_{n=1}^N p \left(y_n | \pmb{x}_n, \pmb{W} \right) \\
p(\tau) = C^+\left(0, \frac{1}{100}\right) \\
p(c^{-2}) = \Gamma(2, 2) \\
p(\pmb{\lambda}|\tau) = \prod_{i=1}^D C^+(0, \tau) \\
p(\pmb{W}|\pmb{\lambda}) = \prod_{d=1}^D \mathcal{N}\left(0, \tilde{\lambda}^{2} \right)
Regression comparison
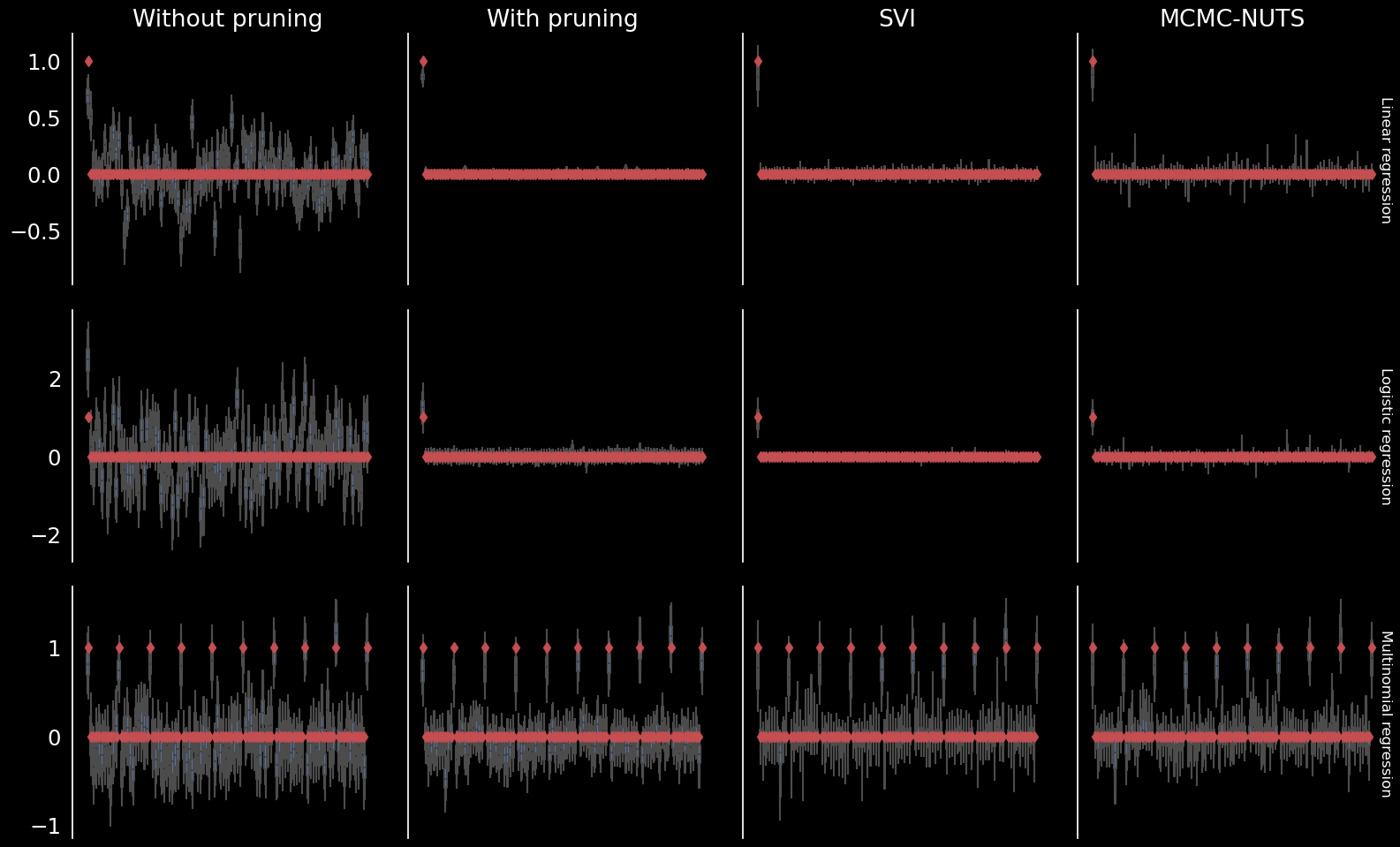
Outline
- Bayesian deep learning
- Structured shrinkage priors
- Bayesian model reduction
- Regression
- Non-linear regression
Simulated data
D_{in} = 100, \: f(\pmb{x}_n, \pmb{W}) = ReLU(x_{n, 1}), \: y_n \sim \mathcal{N}(f(\pmb{x}_n, \pmb{W}), 1)
Normal likelihood
N = 2000, \quad \pmb{x}_n \sim \mathcal{N}_{D_{in}} \left(0, \pmb{I} \right)
D_{in} = 100, \: f(\pmb{x}_n, \pmb{W}) = ReLU(x_{n, 1}), \: y_n \sim \mathcal{Be}\left(s(f(\pmb{x}_n, \pmb{W})\right)
Bernoulli likelihood
D_{in} = 19, D_{out} = 10 \\
f_c(\pmb{x}_n, \pmb{W}) = ReLU(x_{n, c}), \forall c \in \{1, \ldots, D_{out}\} \\
y_n \sim \mathcal{Cat}\left(\pmb{\rho}\right), \: \rho_c \propto e^{f_c}
Categorical likelihood
Neural network model
D_{in} = 100, D_{h} = 20, D_{out}=1 \\
f(\pmb{x}_n, \pmb{W}) = W_2 \cdot ReLU(\pmb{W}_1 \cdot \pmb{x}_{n})
Normal and Bernoulli likelihoods
D_{in} = 10, D_h = 101, D_{out} = 10 \\
f(\pmb{x}_n, \pmb{W}) = W_2 \cdot ReLU(\pmb{W}_1 \cdot \pmb{x}_{n})
Categorical likelihood
\pmb{\beta} = \pmb{W}_2 \cdot \pmb{W}_1
Comparison
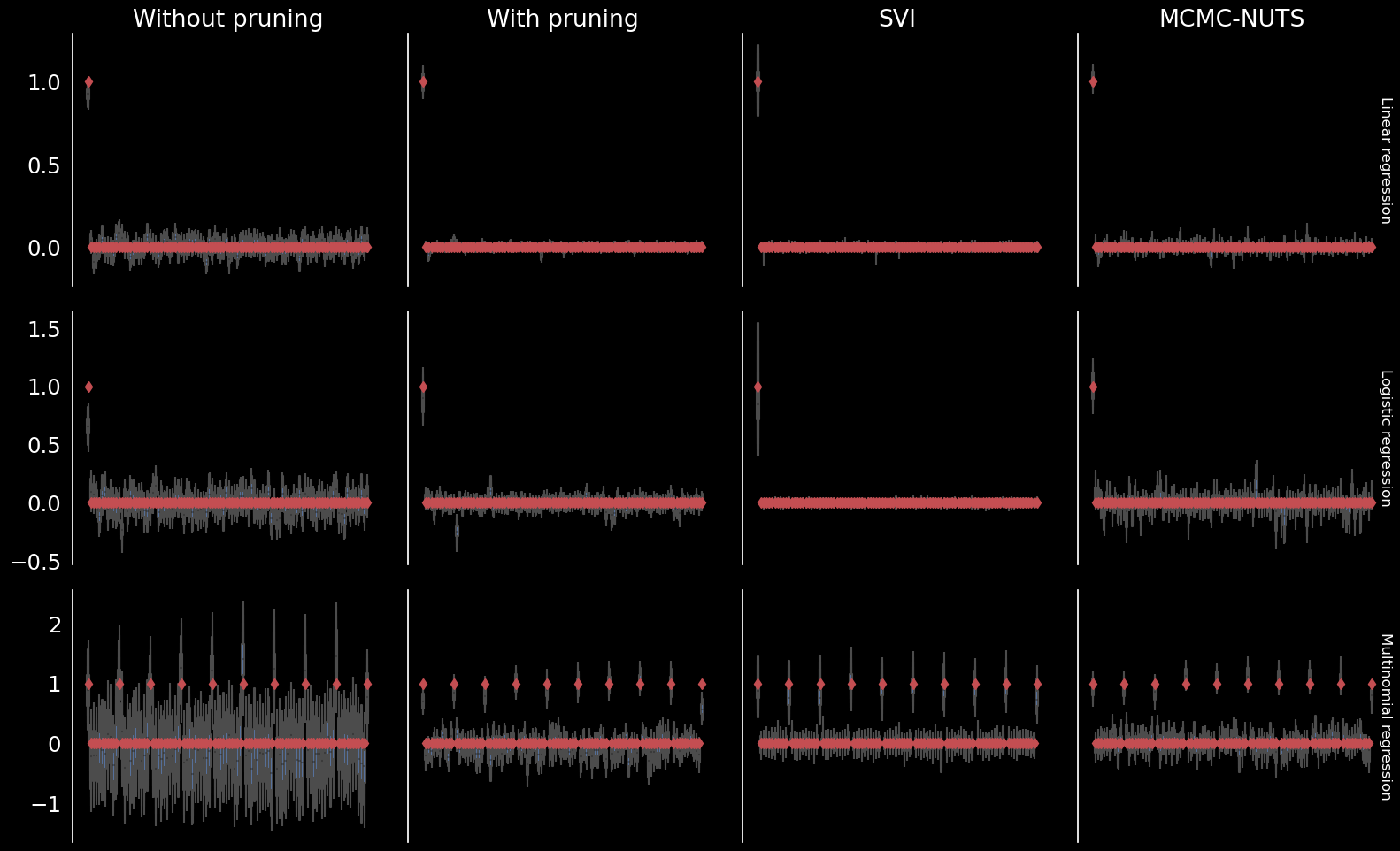
Leave one out cross validation
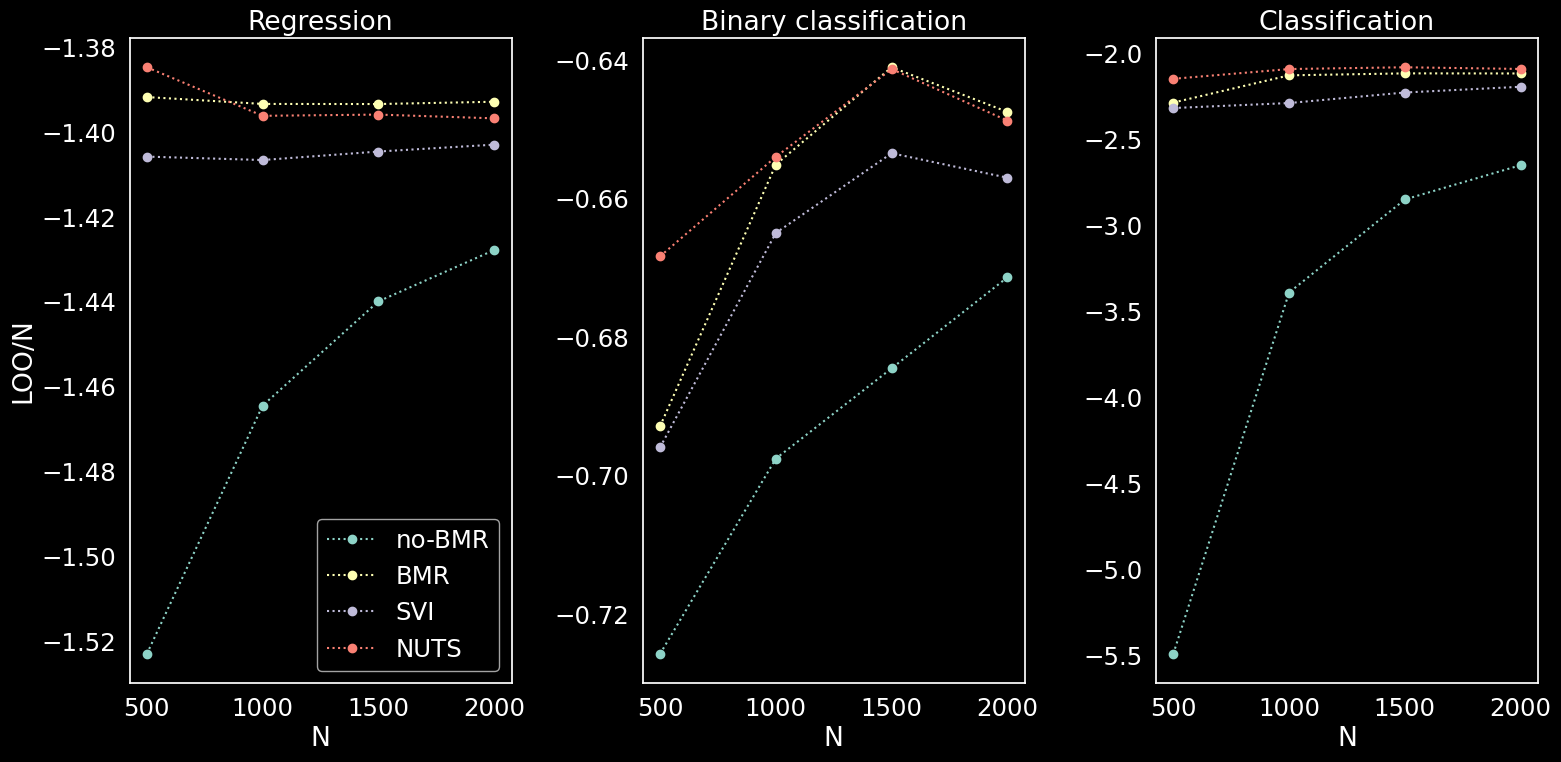
Real data
TODO: UCI Machine learning repository
| label | N | D |
|---|---|---|
| Yacht | 308 | 6 |
| Boston | 506 | 13 |
| Energy | 768 | 8 |
| Concrete | 1030 | 8 |
| Wine | 1599 | 11 |
| Kin8nm | 8192 | 8 |
| Power Plant | 9568 | 4 |
| Naval | 11,934 | 16 |
| Protein | 45,730 | 9 |
| Year | 515,345 | 90 |
Image classification
TODO:
- Compare BMR with SVI, and MAP/MLE.
- Vary data set size, network depth.
- Maybe NUTS can handle some cases?
- Compute relevant values on the testing data set.
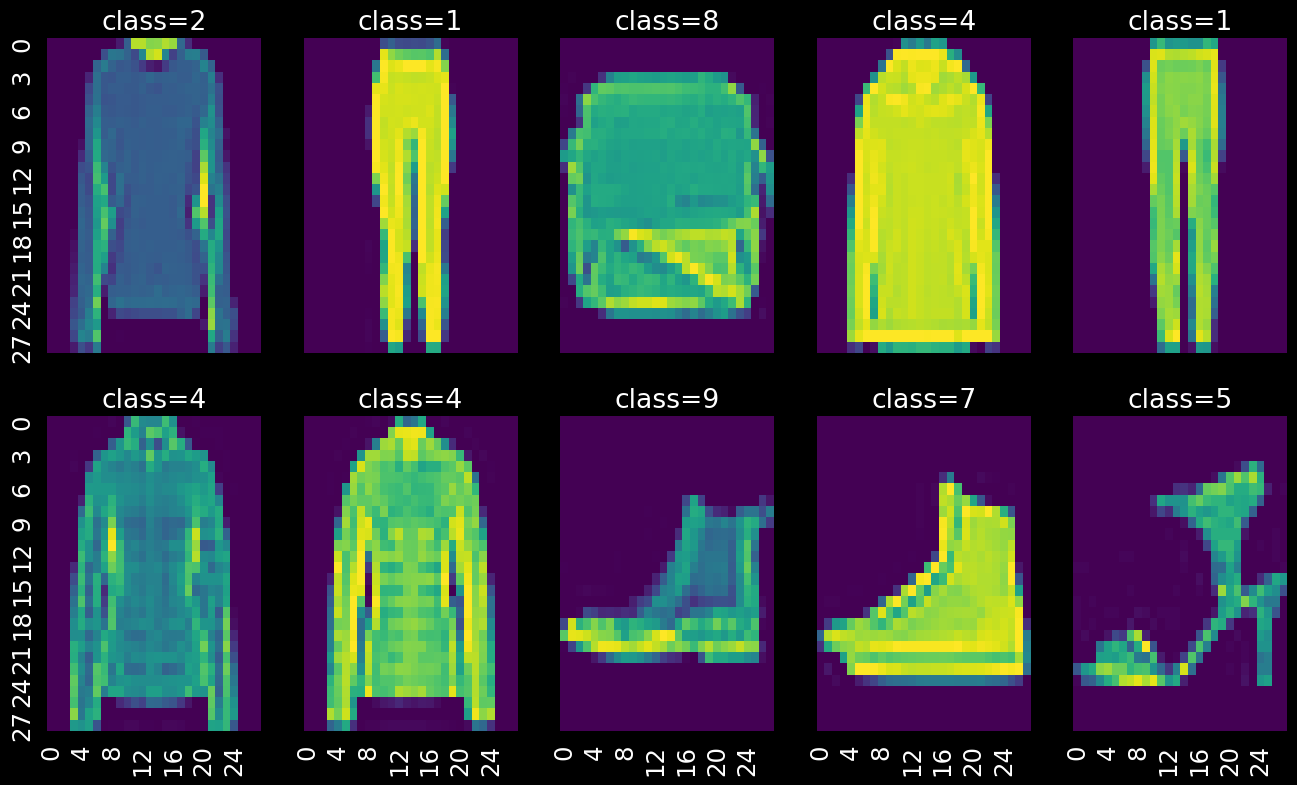
Fashion MNIST
Discussion
BMR seems to work great and has great potential for a range of deep learning applications.
https://github.com/dimarkov/numpc
Might be possible to prune pre-trained models using Laplace approximation.
But ... we can do better and use BMR to formulate Bayesian sparse predictive coding models.
Naturally complements distributed and federated inference problems.
Bayesian model reduction for nonlinear regression
By dimarkov
