Bayesian sparse regression
Dimitrije Marković
DySCO meeting 16.02.2022
Sparse regression in GLMs
\mu_k = \alpha + \sum_{d=1}^D \beta_d x_{d, k} \\
\mu_k = \alpha + \pmb{X}_k \cdot \pmb{\beta} \\
y_k \sim p(y_k|\mu_k, \theta);\:\: \text{for } k \in \{1, \ldots, N\}
Sparse regression in GLMs
Outline
- Bayesian regression
- Hierarchical priors
- Shrinkage priors
- QR decomposition
- Pairwise interactions
Linear regression model
\mu_k = \alpha + \sum_{d=1}^D \beta_d x_{d, k} \\
y_k = \mu_k + \epsilon_k \\
\epsilon_k \sim \mathcal{N}(0, \sigma)
D = 50, N = 200 \\
\alpha = 0, \quad X_k \sim \mathcal{N} \left(0, \pmb{I}_D\right) \\
\beta_{1}, \ldots, \beta_{S} > 0; \quad \beta_{d>S} = 0; \quad S=5 \\
\sigma = 1.
Simulated data
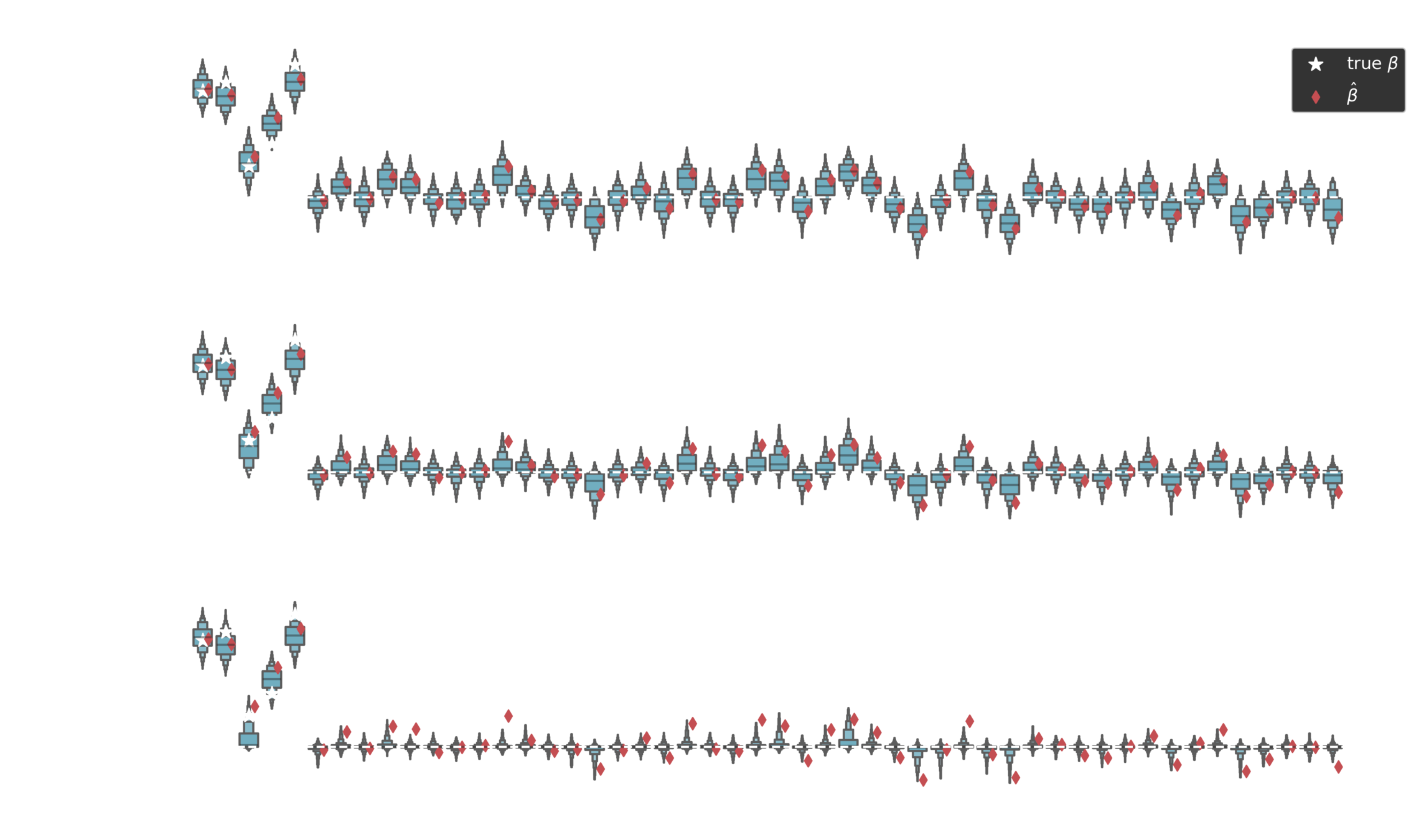
Generative model
p \left(y | \pmb{X}, \pmb{\beta}, \sigma \right) = \mathcal{N} \left(y; \pmb{X} \cdot \pmb{\beta}, \sigma^2 \right) \\
p(\pmb{\beta}) = \mathcal{N}_D\left(\pmb{\beta}; 0, \sigma^2 \tau^2 \pmb{\Lambda} \right) \\
\pmb{\Lambda} = diag(\lambda_1^2, \ldots, \lambda_D^2) \\
\mathcal{D} = \left( \pmb{X}, \pmb{y} \right)
Posterior distribution
p\left(\pmb{\beta}|\pmb{\Lambda}, \tau, \sigma, \mathcal{D} \right) = \mathcal{N}\left(\pmb{\beta}; \bar{\pmb{\beta}}, \pmb{\Sigma} \right) \\
\hat{\pmb{\beta}} = \left( \pmb{X}^T \pmb{X} \right)^{-1} \pmb{X}^T \pmb{y} \\
\bar{\pmb{\beta}} = \tau^2 \pmb{\Lambda} \left( \tau^2 \pmb{\Lambda} + \left(\pmb{X}^T \pmb{X} \right)^{-1} \right)^{-1} \hat{\pmb{\beta}}\\
\pmb{\Sigma} = \sigma^2 \left( \frac{1}{\tau^2} \pmb{\Lambda}^{-1} + \pmb{X}^T \pmb{X} \right)^{-1}
\sigma = 1, \quad \pmb{\Lambda} = \pmb{I}_D, \quad \pmb{X}^T\cdot \pmb{X} \approx N \pmb{I}_D
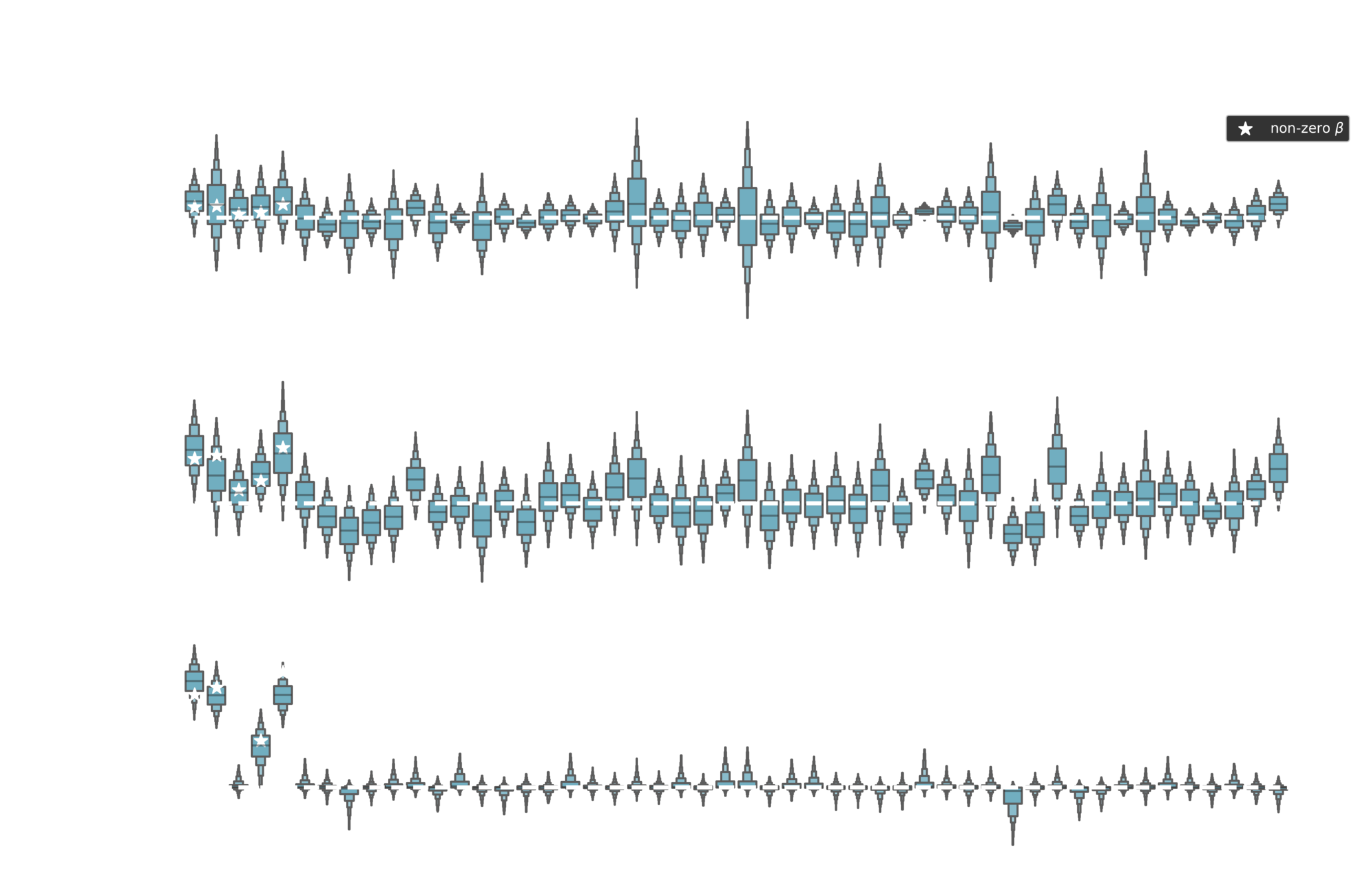
Posterior estimates
Shrinkage factor
Var\left( \pmb{x}_d \right) = s_d, \quad \pmb{X}^T\cdot \pmb{X} \approx N \pmb{I}_D
\bar{\beta}_d = (1 - \kappa_d) \hat{\beta}_d
\kappa_d = \frac{1}{1 + N \tau^2 \lambda_d^2 s_d}
Piironen, Juho, and Aki Vehtari. "Sparsity information and regularization in the horseshoe and other shrinkage priors." Electronic Journal of Statistics 11.2 (2017): 5018-5051.
Generative model
p \left(y | \pmb{X}, \pmb{\beta}, \sigma \right) = \mathcal{N} \left(y; \alpha + \pmb{X} \cdot \pmb{\beta}, \sigma^2 \right) \\
p(\pmb{\beta}) = \mathcal{N}_D\left(\pmb{\beta}; 0, \sigma^2 \tau^2 \pmb{\Lambda} \right) \\
\pmb{\Lambda} = diag(\lambda_1^2, \ldots, \lambda_D^2) \\
p(\alpha) = \mathcal{N}(0, 10) \\
p\left( \sigma^2 \right) = \Gamma^{-1} \left(2, 2 \right) \\
\mathcal{D} = \left( \pmb{X}, \pmb{y} \right)
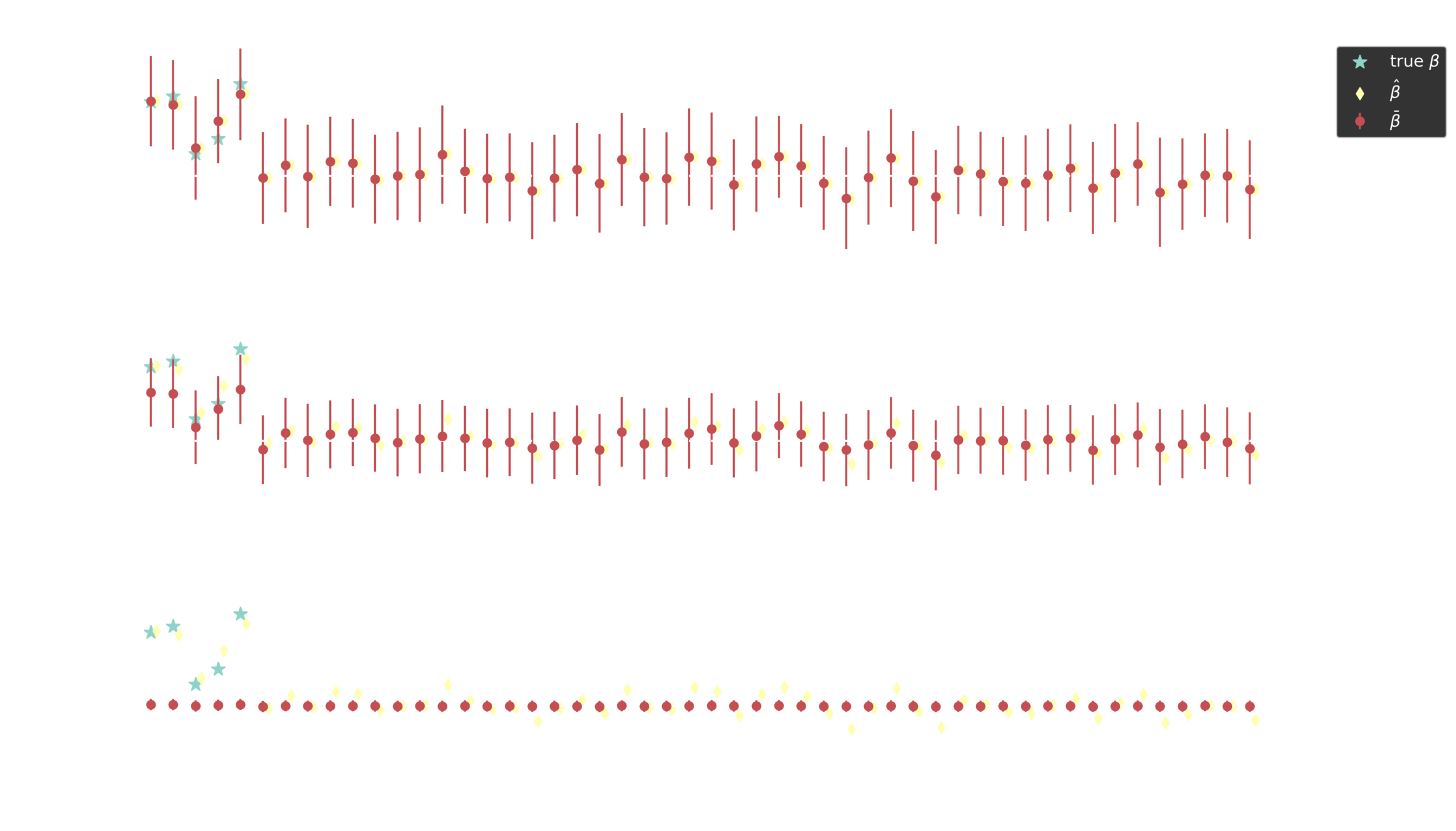
Posterior estimates
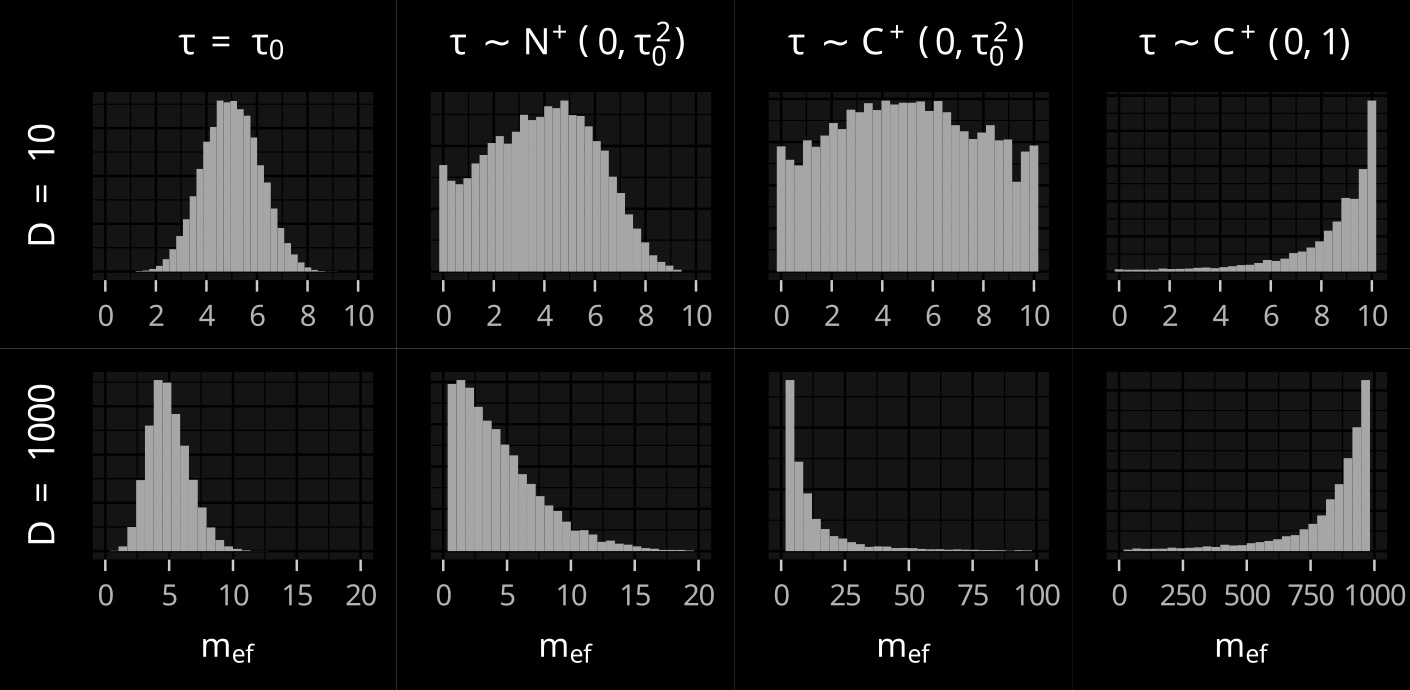
Horseshoe prior
\kappa_d = \frac{1}{1 + N \tau^2 \lambda_d^2 s_d}
Piironen, Juho, and Aki Vehtari. "Sparsity information and regularization in the horseshoe and other shrinkage priors." Electronic Journal of Statistics 11.2 (2017): 5018-5051.
\lambda_d \sim C^+(0, 1)
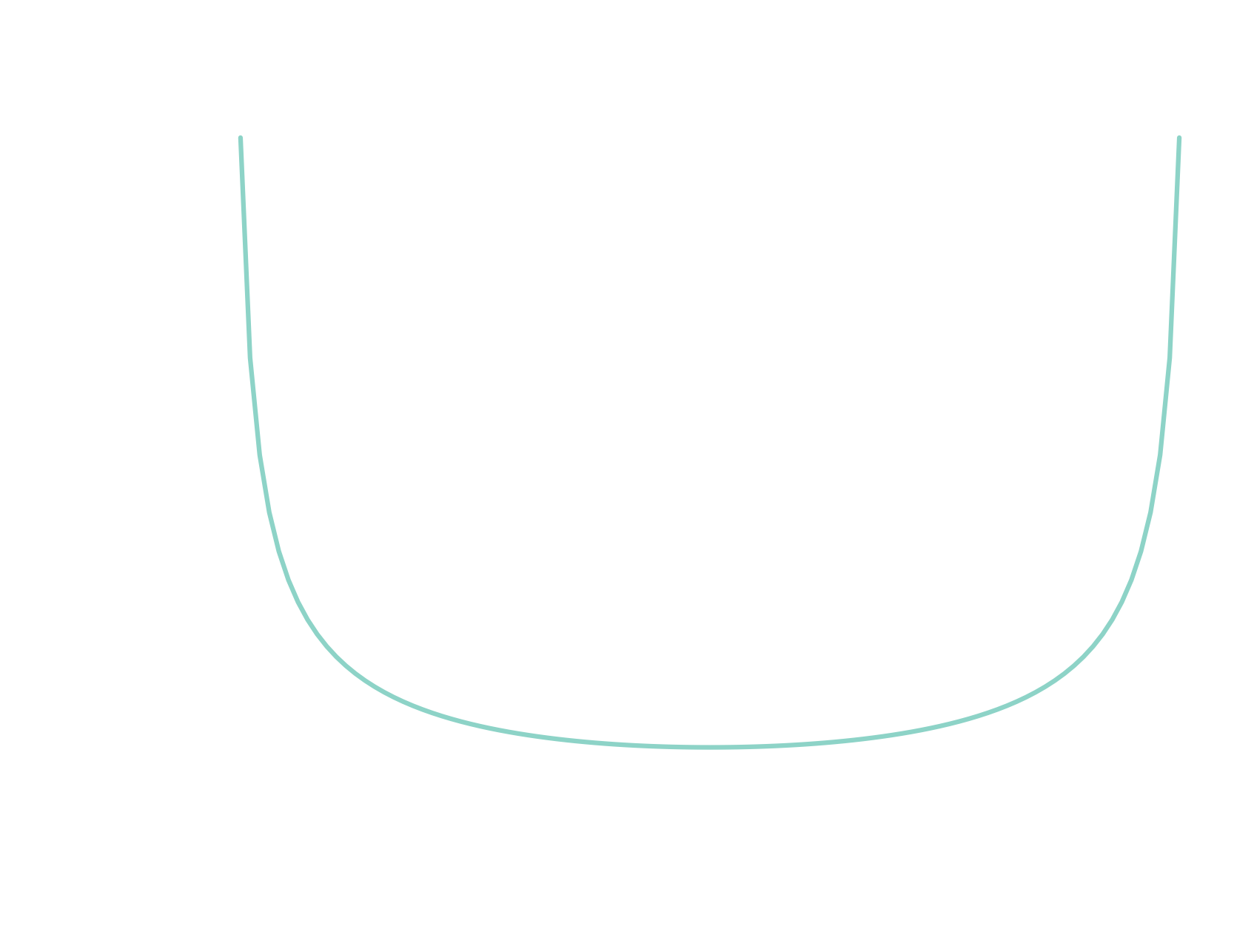
Half-Cauchy distribution
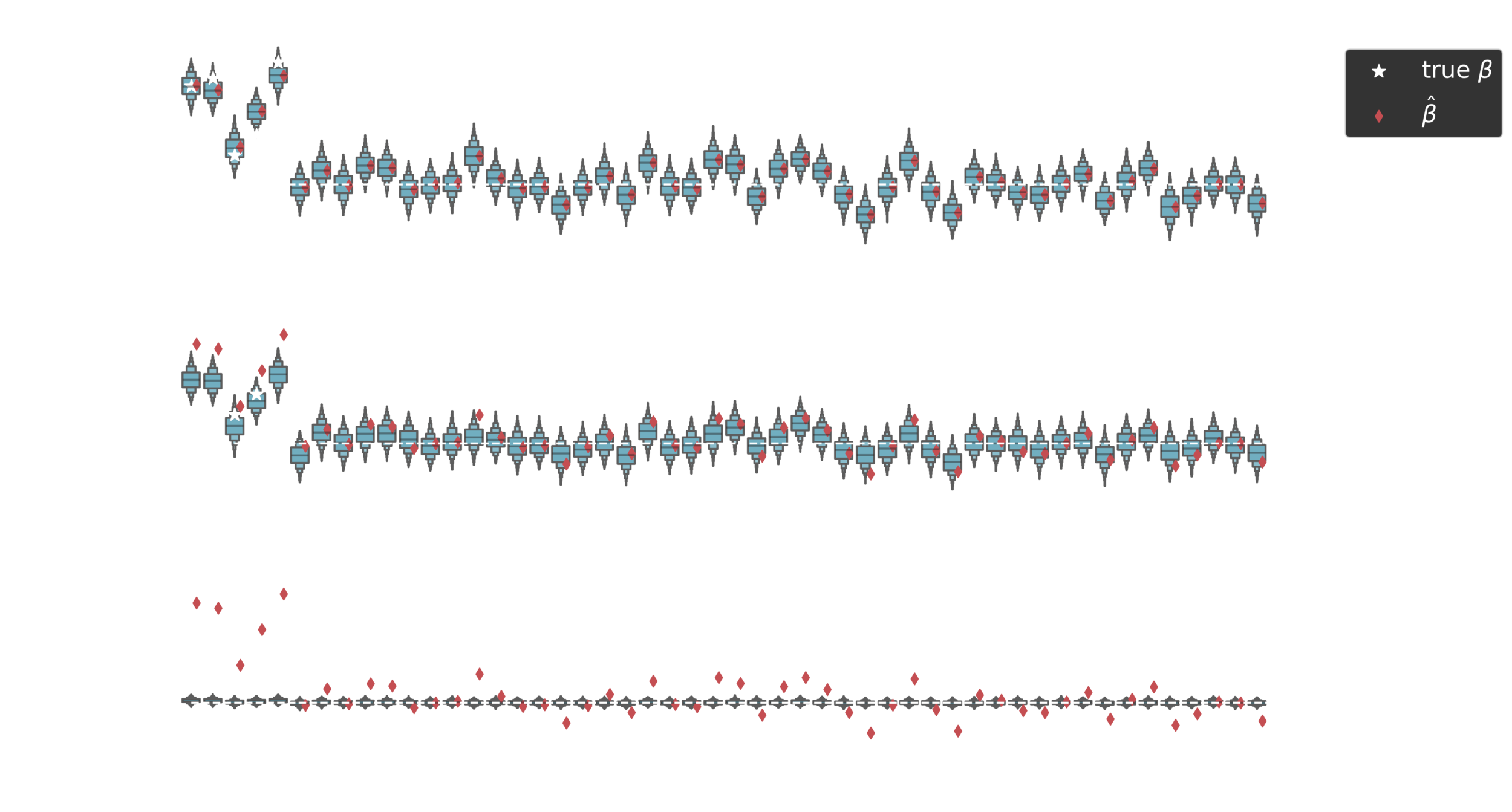
Hierarchical generative model
p\left( \sigma^2 \right) = \Gamma^{-1} \left(2, 2 \right) \\
p\left( \lambda_d \right) = C^+(0, 1) \\
p(\beta_d|\lambda_d) = \mathcal{N}\left(0, \sigma^2 \tau^2 \lambda_d^2 \right) \\
p(\alpha) = \mathcal{N}(0, 10) \\
p \left(y | \pmb{X}, \pmb{\beta}, \sigma \right) = \mathcal{N} \left(y; \alpha + \pmb{X} \cdot \pmb{\beta}, \sigma^2 \right)
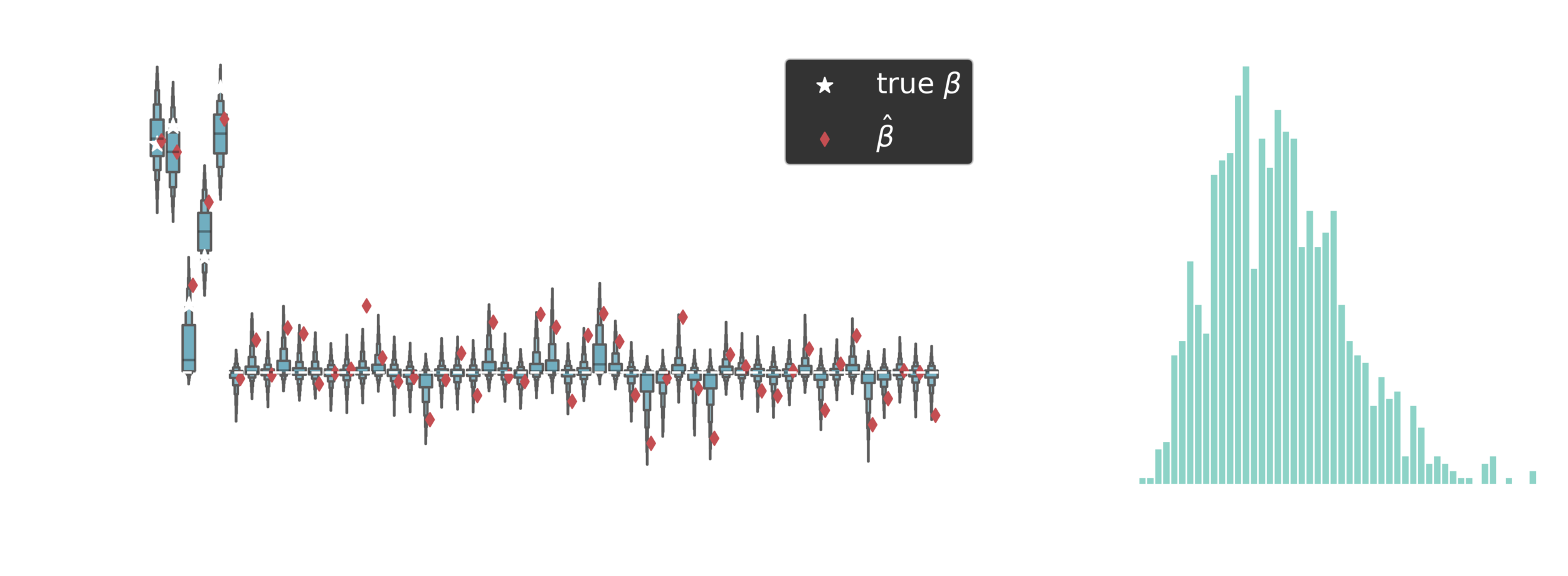
Posterior estimates
Non-zero coefficients
\tau \sim C^{+}(0, \tau_0^2)
Piironen, Juho, and Aki Vehtari. "Sparsity information and regularization in the horseshoe and other shrinkage priors." Electronic Journal of Statistics 11.2 (2017): 5018-5051.
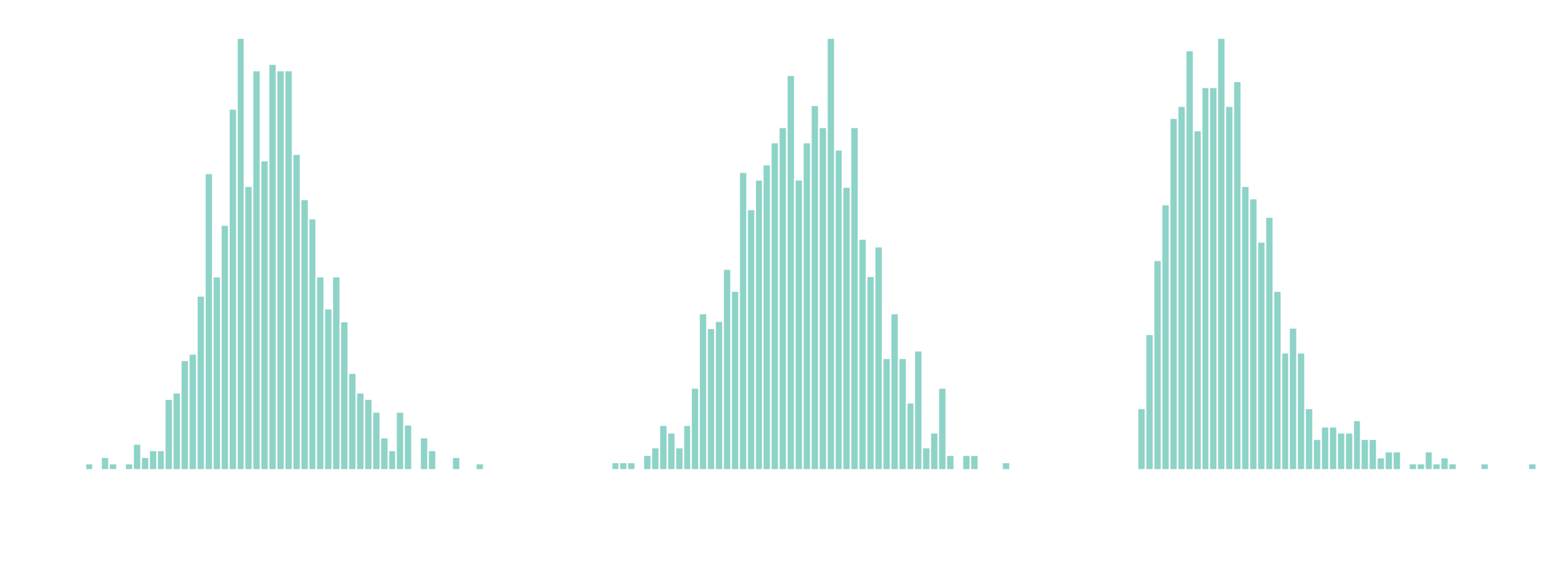
Effective number of
non-zero coefficients
m_{eff} = \sum_d (1 - \kappa_d)
Expected effective number
p_0 = E[m_{eff}|\tau] = \frac{\tau \sqrt{N}}{1 + \tau \sqrt{N}} D
\tau_0 = \frac{p_0}{D - p_0} \frac{1}{\sqrt{n}}
Effective number
Piironen, Juho, and Aki Vehtari. "Sparsity information and regularization in the horseshoe and other shrinkage priors." Electronic Journal of Statistics 11.2 (2017): 5018-5051.
N = 100,\:\: \sigma=1, p_0 = 5
Hierarchical shrinkage
\sigma^2 \sim \Gamma^{-1} \left(2, 2\right)\\
\tau_0 = \frac{p_0}{D - p_0} \frac{1}{\sqrt{n}} \\
\tau \sim C^+(0, \tau_0^2) \\
\lambda_d \sim C^+(0, 1) \\
\beta_d \sim \mathcal{N} \left(0, \sigma^2 \tau^2 \lambda^2_d \right) \\
\alpha \sim \mathcal{N}(0, 10)
Piironen, Juho, and Aki Vehtari. "Sparsity information and regularization in the horseshoe and other shrinkage priors." Electronic Journal of Statistics 11.2 (2017): 5018-5051.
prior constraint on the
number of nonzero coefficients
\( \rightarrow \)
Posterior estimates
Posterior estimates
Outline
- Bayesian regression
- Hierarchical priors
- Shrinkage priors
- QR decomposition
- Pairwise interactions
QR decomposition
\pmb{X}_k \sim \mathcal{N}_D \left( 0, \pmb{I}_D \right)
\pmb{X}^c_k \sim \mathcal{N}_D \left( 0, \pmb{\Sigma} \right)
\pmb{X}^c = \pmb{Q} \pmb{R}
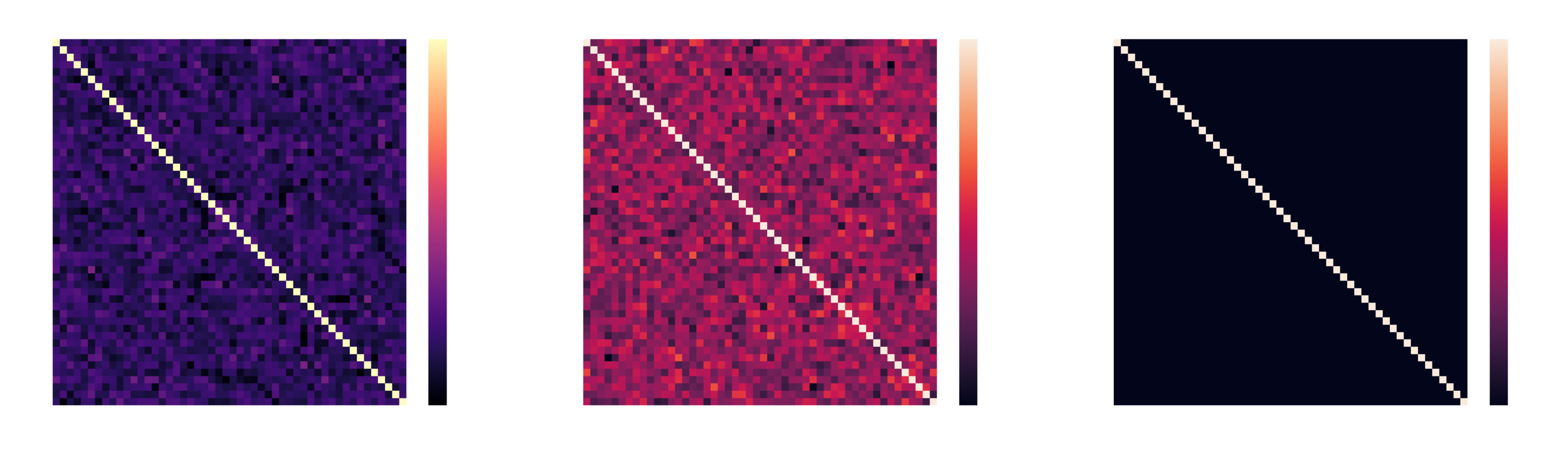
Simulated data
D = 50, N = 200 \\
\alpha = 0, \quad X_k^c \sim \mathcal{N} \left(0, \pmb{\Sigma} \right) \\
\beta_{1}, \ldots, \beta_{S} > 0; \quad \beta_{d>S} = 0; \quad S=5 \\
\sigma = 1.
Posterior estimates
Outline
- Bayesian regression
- Hierarchical priors
- Shrinkage priors
- QR decomposition
- Pairwise interactions
Pairwise Interactions
Agrawal, Raj, et al. "The kernel interaction trick: Fast bayesian discovery of pairwise interactions in high dimensions." International Conference on Machine Learning. PMLR, 2019.
\mu_k = \alpha + \sum_{i=1}^D \left[ \beta_i x_{i, k} + \sum_{j>i} \beta_{ij} x_{i, k} x_{j, k} \right] \\
y_k \sim p(y_k|\mu_k, \theta);\:\: \text{for } k \in \{1, \ldots, N\}
\mu_k = \alpha + \tilde{\pmb{X}}_k \cdot \tilde{\pmb{\beta}} \\
linear regression?
Structural prior
Agrawal, Raj, et al. "The kernel interaction trick: Fast bayesian discovery of pairwise interactions in high dimensions." International Conference on Machine Learning. PMLR, 2019.
\sigma^2 \sim \Gamma^{-1} \left(2, 2\right)\\
\alpha \sim \mathcal{N}(0, 10)
\tau_0 = \frac{p_0}{D - p_0} \frac{1}{\sqrt{n}} \\
\tau_1 \sim C^+(0, \tau_0^2) \\
\lambda_i \sim C^+(0, 1) \\
\beta_i \sim \mathcal{N} \left(0, \sigma^2 \tau_1^2 \lambda^2_i \right) \\
\tau_2 \sim C^+(0, \tau_1^2) \\
\beta_{ij} \sim \mathcal{N} \left(0, \sigma^2 \tau_2^2 \lambda^2_i \lambda^2_j \right) \\
The kernel interaction trick
Agrawal et al. demonstrates how one can express the linear regression problem (with pairwise interactions) as a Gaussian process model using specific kernel structure.
The Gaussian process models have better scaling with D, but further approximations are needed for larger N.
To me it is unclear if the approach can be applied to nonlinear GLMs.
Discussion
Hierarchical shrinkage priors are essential for separating signal from noise in the presence of correlations.
Structural shrinkage priors help separate linear
and pairwise contributions to the "responses".
https://github.com/dimarkov/pybefit
Generalises to Logistic regression, Poisson regression, etc.
Bayesian sparse regression
By dimarkov
