ECSE 321 - Tutorial 7

Dominic Charley-Roy

https://github.com/dominiccharleyroy

dominic.charley-roy @ mail.mcgill

Path Finding

Finding our way...

• Pathfinding is a class of algorithms which can find the route between two points.
• Algorithms exist for solving different complexities of problems:
  • Are we in a 2D or 3D space?
  • Are there obstacles?
  • Are there moving obstacles?
  • How much time do we have to make a decision?
  • Will the end point change

Bomberman

Our particular problem

• We have a 2D grid.
• There are obstacles on the grid. 
  • These obstacles can appear/dissapear!
• We'd like our game to run smoothly, so there shouldn't be any discernible "thinking" phase.
• Enemies need to use 2 algorithms:

1. Determining if Bomberman is within a certain distance.
2. Finding the path to Bomberman / their next move position

Euclidean Distance

This is a formula for determining the distance between two points. You can think of this as if you drew a straight line between two points and measured it with a ruler.

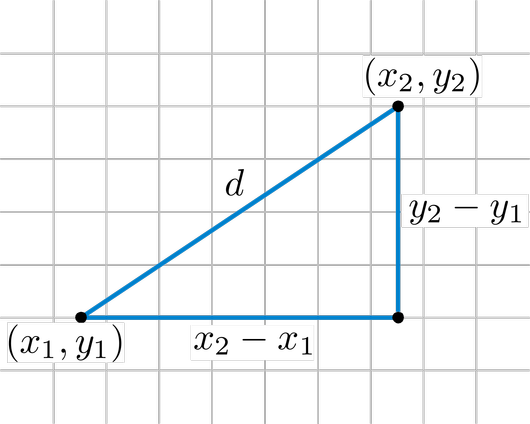
Euclidean Distance Cont'd.

Given the points (x1, y1) and (x2, y2), the distance is calculated by:

double distance = Math.sqrt(
    Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));

This can now help us answer questions such as Is Bomberman within the distance d​ from an enemy.

As the distance is initially a double, it is common to round it to work with it as an integer. Then we can check if distance <= 3. If we left it as a double, we have to worry about accuracy.

Taxicab Distance

This is a different metric​ for determining the distance between two points. Since we are working on a 2D grid, we can think of distance like we would in a regular city. 

If a taxicab needs to drive up 3 blocks and then right 4 blocks to get you to your house, the distance is 7!

Taxicab Distance Cont'd

Given two points (x1, y1) and (x2, y2) the taxicab distance is calculated:

int distance = Math.abs(x1 - x2) + Math.abs(y1 - y2);

Note: Taxicab distance gives you the distance as an int!

Also note that Taxicab distance only really makes sense if your points are integers (eg. no 10.5)

Distance Calculation Recap

• Euclidean distance draws a line between two points and measures it
• Taxicab is based on a city grid, and calculates the number of blocks between two points. (Only works for integer points)
• Both are heuristics and thus give therefore answers for distances.
• Neither take obstacles into consideration!
• DEMO TIME!!!

Finding the Shortest Path

A*

The A* Algorithm

• The A* algorithm lets you find the shortest distance between two points.
• It uses some kind of distance calculation - we'll be using Euclidean!
• Our particular scenario:
  • 2D grid where entities can move in 4 directions.
  • Some cells are obstacles. 
• Fast enough that we can recalculate easily so this supports the map changing.

Shortest Distance?

• The definition of shortest distance changes on the problem.
• In our case, we mean the shortest number of moves to get from one point to another. 
  • We assume that moving in any direction "costs" the same.
• Some problems are different! Suppose you are making Google Maps - there are actual distances between cities, and we want to find the path for which you have to drive the least!

Important Note

• A* isn't the only path finding algorithm - Dijkstra's algorithm is another famous one!
• Ideally, we want our algorithm to not only give us the shortest distance but the path that will give us this distance as well!
  • For our monsters, it's no good knowing the shortest distance to get to Bomberman if we don't know how to move!

Some Background:
The Queue

• A Queue is a standard data structure which works like a line at a bank. You put items into it (enqueue) and can remove the item which has been in the queue for the longest (dequeue).
  • People enqueue in the bank line and the person who was here first gets served first.

Some Background:
The Priority Queue

• A Priority Queue is a special type of Queue which is sorted based on some ordering.
  • Instead of dequeue removing the first element, it removes the one with the highest priority.
• Java provides the PriorityQueue<T> class.
  • Note that either the objects you put in the priority queue should be Comparable or you should provide a Comparator
  • This has an add method (enqueue) and add method (dequeue).
  • The queue is automatically sorted for you.

Some A* Terms

• A* works by exploring potential shortest paths one square at a time.
• We maintain a priority queue of candidates, which are squares which have not yet been explored but are adjacent to a square which has been. 
  • Here we order them based on how good the candidate is according to a heuristic (huh?!)
• We also maintain a set of closed points, which are squares that have already been seen and that we don't need to look at again.

The Basic Idea

• Initially only the starting point is in the queue of candidates.
• At each round, we dequeue "best" candidate.
  • If the candidate is already in the closed list, ignore it.
  • If the best candidate is the end point, we've found the shortest path!
  • If not, we process the point and add it to the closed list.
• If our priority queue is empty and we never reached the end point, then there is no possible path!

"Best"?

Points are evaluated based on the sum of a "past" score and a "future" score.

• The past score is the length of the path from the starting point to this point.
• The future score is a guess at the length of the point to the finish.
  • We have to guess since we don't know what obstacles we may see! We use a distance function here to guess!
• The best therefore has the lowest score:

score = pastDistance + futureDistance;

What does a Point have?

• For our purposes, a Point object will have the following properties:
  • int x, y representing their coordinates on the grid.
  • Point parent a link to the point that was used tor each this point (or null if it's the starting point)
  • int pastScore (should be parent.pastScore + 1)
  • Note: futureScore can just be calculated so we don't need to store it!
• Once we've extracted the end point as the best candidate, we can build the path by repeatedly getting the parent's coordinates!

Processing a Point

• When we process a best candidate, we want to look at all the adjacent nodes and consider them all as potential candidates!
• For processing, we look each the 4 nodes (neighbors) next to the candidate. For each neighbor:
  • If you can't walk to the neighbour (eg. it is a wall), ignore it.
  • If the neighbour is in the closed list, ignore it.
  • Create a new Point object representing the neighbour with the candidate as its parent and add it to the candidate queue.

The Candidate Queue

• Remember that the candidate queue is sorted. In our case, the best candidate has the lowest score.
• As we process nodes, we may visit a neighbour which is already in the candidate list but has not been processed yet! It's important to allow for this, as we may have found a better path!
  • Note: Some priority queues let you update nodes, so you could use that instead of having a point appear multiple times in the candidate list.
  • To keep this simple, we allow a point multiple times in the candidate list and simply check if it is already closed when processing.

Interactive Demo Time!

http://qiao.github.io/PathFinding.js/visual/

Initializing Pseudocode

List<Point> getShortestPath(startX, startY, endX, endY) {
    // Create the queue of candidates.
    PriorityQueue<Point> candidates = new PriorityQueue<Point>(
        new PointComparator(endX, endY));
    // Create a boolean 2D array representing if a given point 
    // is in the closed list.
    boolean[][] closed = new boolean[sizeX][sizeY];

    // Add the starting point to the list of candidates.
    candidates.add(new Point(startX, startY, null, 0));

    // ...
}

Main Pseudocode

// Keep going until there are no candidates left.
while (!candidates.isEmpty()) {
    // Get the best candidate.
    Point candidate = candidates.poll();
    // If the candidate is the end point, we've found the 
    // shortest path!
    if (candidate.x == endX && candidate.y == endY) 
        return buildPath(candidate);
    // If the candidate is already closed, ignore it.
    if (closed[candidate.x][candidate.y])
	continue;
    // Look at each neighbor of the candidate.
    for (Point neighbor : candidate.getNeighbors()) {
        // If the neighbor is closed or cannot be walked to,
        // it is ignored.
	if (blocked[neighbor.x][neighbor.y] ||
        	closed[neighbor.x][neighbor.y]) 
            continue;	  
        // Add the candidate.
        candidates.add(neighbor);
    }
    // Close the candidate.
    closed[candidate.x][candidate.y];
}
// No path found!
return null;

Comparator Pseudocode

We have to create a comparator specifically tailored to our end point to calculate the distance!

public class TestComparator implements Comparator<Point> {
	
	public TestComparator(int endX, int endY) {
		// Create a comparator based on a given end point.
		this.endX = endX;
		this.endY = endY;
	}
	
	public int compare(Point p1, Point p2) {
		// Calculate past + future score for both points.
		int score1 = p1.pastScore + distance(p1.x, p1.y, endX, endY);
		int score2 = p2.pastScore + distance(p2.x, p2.y, endX, endY);
		// Point 1 should be before Point 2 if score1 has a lower value.
		return score1 - score2;
	}

	public int distance(x1, y1, x2, y2) {
		// Insert distance function here!
	}
}

getNeighbors Pseudocode

public class Point {
	// ...
	public List<Point> getNeighbors() {
		List<Point> points = new ArrayList<>();
		
		// Up direction
		// Check if this point is within the boundaries of the map.
		if (this.y > 0) {
			// Create the up neighbor with the proper coordinates. 
			// The neighbor will have this point as its parent and
			// takes the pastScore and adds 1 to represent the move.
			Point upNeighbor = new Point(
                                this.x, this.y - 1,
                                this, this.pastScore + 1);
			points.add(upNeighbor);
		}
		
		// Other directions...
		
		return points
	}
}

Recap

• Distance functions let you determine if a point is within a given range from another point. Different ways of calculating this exist!
  • Euclidean distance draws a line between 2 points and measures it.
  • Taxicab distance pretends we are driving through city blocks to get to the point (can't go through buildings).
• Path finding algorithms such as A* let you find the shortest path between 2 points.