第五章 曲线运动
在本章中我们将：
1．认识和理解位移、速度、加速度等物理量。
2．经历质点模型的建构过程，初步学会测量物体的瞬时速度。
3．学习用文字、关系式、图像描述简单的实际运动。
第一节
曲线运动
物体沿曲线所做的运动叫曲线运动（curvilinear motion）
第一节
曲线运动
常见的曲线运动
第一节
曲线运动
一、曲线运动的速度方向
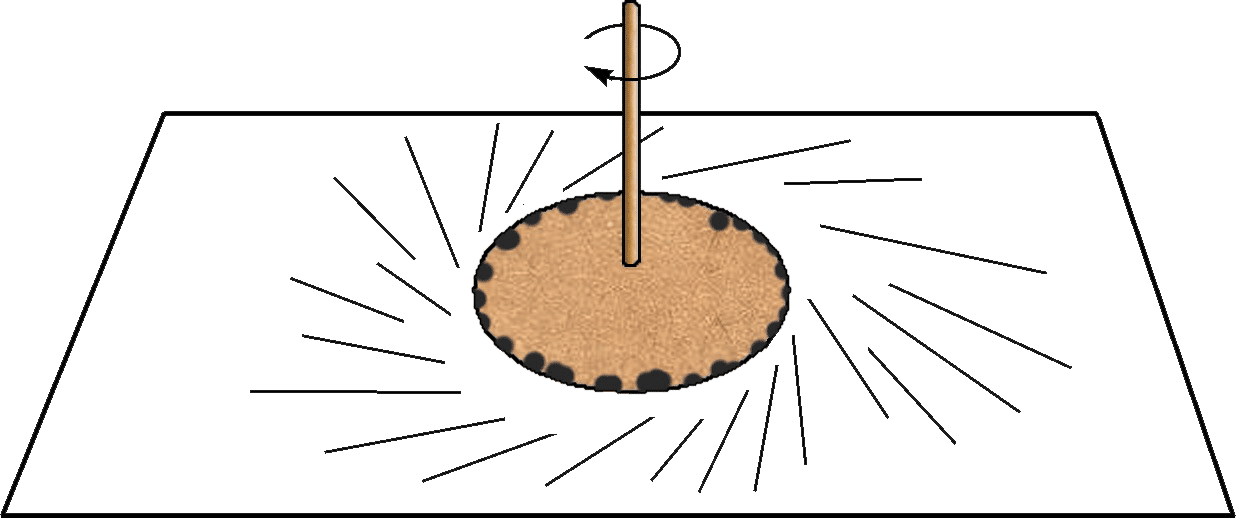
纸板陀螺上飞溅的墨滴
现象：墨水沿圆纸板的切线方向飞出
第一节
曲线运动
一、曲线运动的速度方向
旋转砂轮上飞溅的火星
第一节
曲线运动
一、曲线运动的速度方向
做曲线运动物体的速度的方向是时刻改变的，物体在某一点的瞬时速度方向沿曲线在该点的切线方向。
速度是矢量，速度方向改变，就表示速度发生了变化。所以曲线运动是变速运动，做曲线运动的物体具有加速度。
第一节
曲线运动
二、物体做曲线运动的条件
条件：物体所受合力的方向与其速度方向不在一条直线上
第一节
曲线运动
二、物体做曲线运动的条件
条件：物体所受合力的方向与其速度方向不在一条直线上
v
F_合 = f
第一节
曲线运动
二、物体做曲线运动的条件
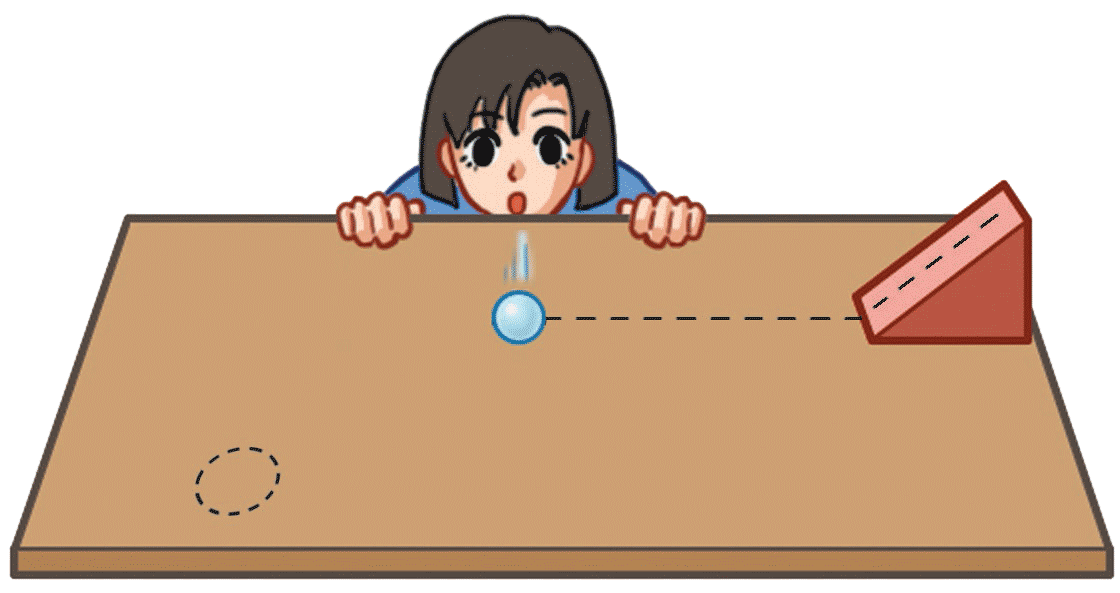
在水平桌面上，一个乒乓球沿斜面滚下后做直线运动。从侧面用力吹乒乓球，使乒乓球运动经过指定位置，应该如何吹才能完成任务？
第一节
曲线运动
三、运动的合成与分解
如何研究曲线运动？
可以把曲线运动分解为两个相互垂直的方向的运动
x
水平方向匀速直线
y
竖直方向自由落体
第一节
曲线运动
三、运动的合成与分解
水平分位移
竖直分位移
合速度
竖直分速度
合位移
水平分速度
\(s\)
运动的叠加原理
一个运动可以看成两个或几个运动的合成或叠加。
独立性：这两个或几个运动是同时进行的且互不干扰。
等时性：合运动、分运动用时相同。
运动的合成与分解仍遵循平行四边形定则
第一节
曲线运动
三、运动的合成与分解
若两个分运动都是匀速直线运动，则合运动也是匀速直线运动
s
x
y
v
v_y
v_x
\theta
\left\{ \begin{array}{l}x = {v_x}t\\y = {v_y}t\end{array} \right.
s = \sqrt {{x^2} + {y^2}}
v = \sqrt {v_x^2 + v_y^2}
\tan \theta = \frac{{{v_y}}}{{{v_x}}} = \frac{y}{x}
第一节
曲线运动
三、运动的合成与分解
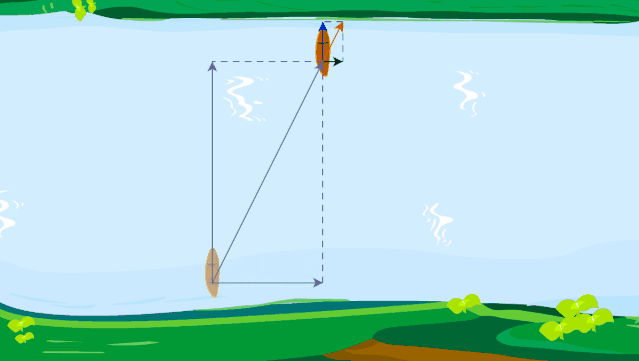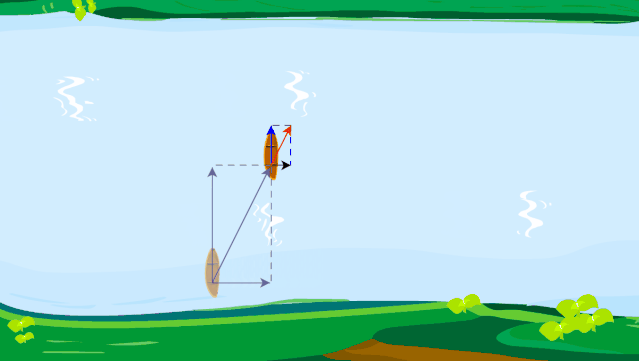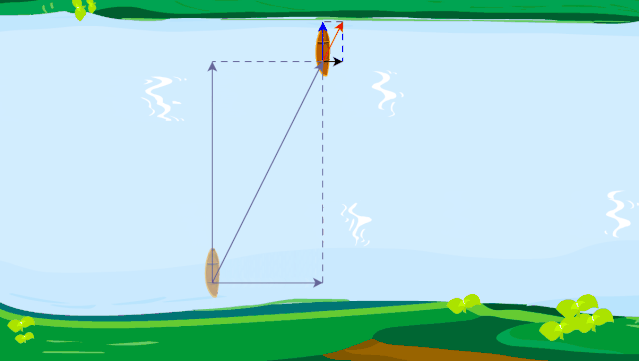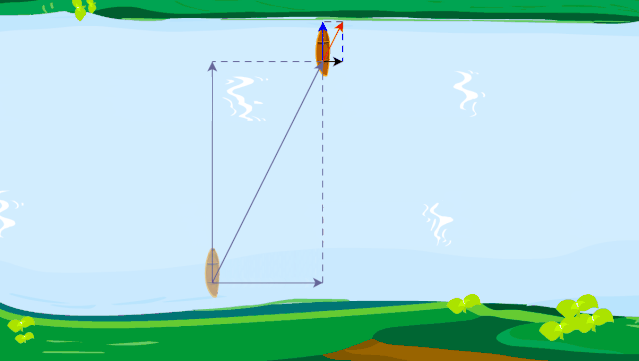
设江水的流速为 6 km/h，轮船在静水中行驶的速度为 12 km/h。当驾驶员驾驶轮船垂直向对岸方向航行时，轮船实际行驶的方向如何？速度大小为多少？如果江面宽 200 m，轮船将行驶到对岸何处？
第一节
曲线运动
三、运动的合成与分解
河宽 \(d\) = 100 m，水速为 \(v_水\) = 3 m/s，小船在静水中的航行速度为 \(v_船\) = 5 m/s，
（1）当小船船头方向垂直河岸行驶时，求船的实际运动速度大小；过河时间，到达对岸时向下游方向走的距离。
（2）为使小船到达正对岸，小船船头方向应偏向__________（选填“上”或“下”）游，求与河岸所成的角度，以及此时小船过河所需的时间。
第二节
平抛运动
第二节
平抛运动
一、抛体运动与平抛运动
以一定速度抛出，在空气阻力可以忽略、只在重力作用下的运动叫做抛体运动。
常见的抛体运动
若抛出物体的初速度沿水平方向，叫做平抛运动。
竖直上抛
平抛
斜抛
第二节
平抛运动
二、平抛运动的规律
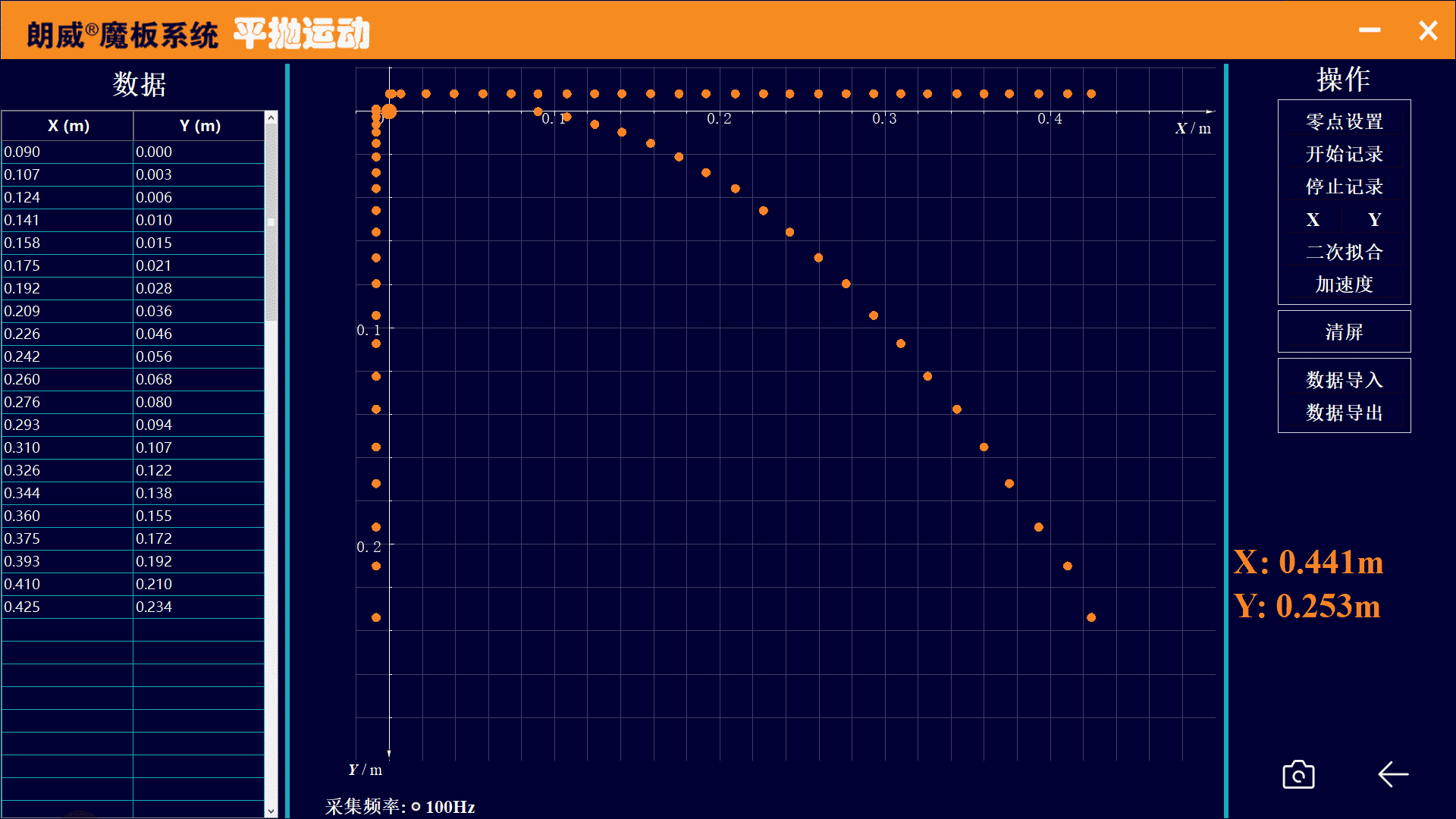
电磁魔板探究平抛运动的规律
第二节
平抛运动
二、平抛运动的规律
水平方向为匀速直线运动
竖直方向为自由落体运动
第二节
平抛运动
二、平抛运动的规律
\left\{ \begin{array}{l}x = {v_0}t\\y = {\frac{1}{2}}gt^2\end{array} \right.
s = \sqrt {{x^2} + {y^2}}
v = \sqrt {v_x^2 + v_y^2}
\tan \theta = \frac{{{v_y}}}{{{v_x}}} = \frac{gt}{v_0}
\left\{ \begin{array}{l}v_x = {v_0}\\v_y = gt\end{array} \right.
\tan \alpha = \frac{{{y}}}{{{x}}} = \frac{gt}{2v_0}
第二节
平抛运动
二、平抛运动的规律
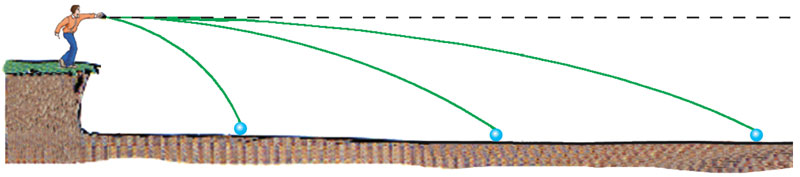
距地面相同高度，将几个物体以不同的初速度自同一点水平抛出，这些物体飞行的时间相等吗？
第二节
平抛运动
三、平抛运动实验
现象：两球始终同时落地
结论：平抛运动在竖直方向上做自由落体运动
摆锤
弹性金属片
第二节
平抛运动
三、平抛运动实验
斜槽
调平螺栓
挡板
竖直板
第二节
平抛运动
三、平抛运动实验
斜槽出口槽保持水平
小球每次应从同一位置由静止释放
原点O为小球球心
第二节
平抛运动
三、平抛运动实验
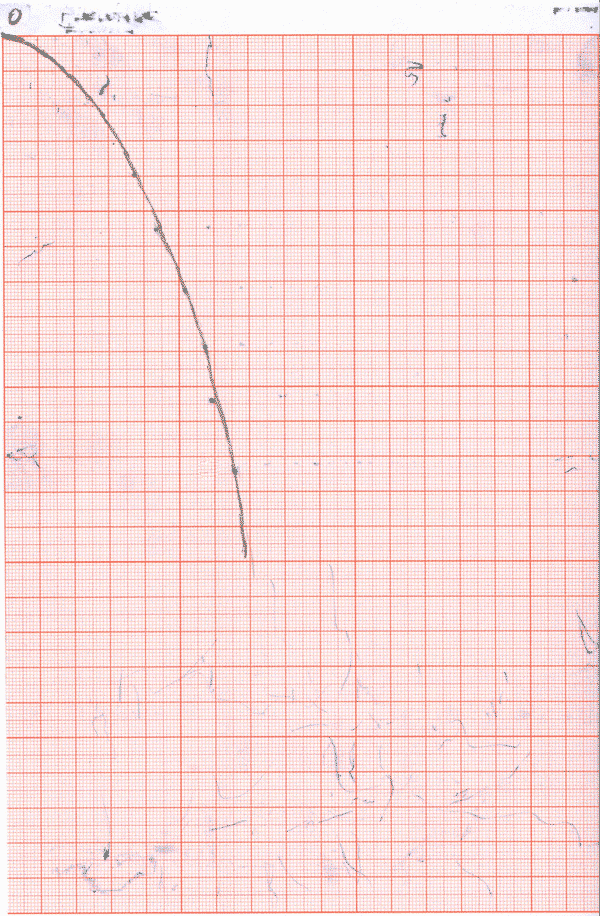
光滑曲线连接
y
5y
3y
1.8 cm
1.9 cm
1.9 cm
y
x
第二节
平抛运动
三、平抛运动实验
“天宫二号“上的空间冷原子钟
第三节
圆周运动
第三节
圆周运动
一、圆周运动与匀速圆周运动
物体做圆周运动时，如果在任意相等时间内通过的弧长总是相等，这种运动叫匀速圆周运动（uniform circular motion）。
常见的圆周运动
注意
洗衣机滚筒、旋转盘、指针本身在转动，不是匀速圆周运动
第三节
圆周运动
二、描述圆周运动的物理量
1
线速度 \(v \)
v= \frac{s}{t}
方向：该位置圆周的切线方向
s（弧长）
注意
单位：m/s
速度大小不变，方向不断变化，
因此，匀速圆周运动是变速曲线运动
第三节
圆周运动
二、描述圆周运动的物理量
月球绕地球的运动和地球绕太阳的运动，都可近似看成是匀速圆周运动。
地球说：“你怎么这么慢？我绕太阳运动 1 s 能走 29.79 km，你绕我运动 1 s 才走 1.02 km。”
月球说：“你可别这么说，你要用一年时间才绕太阳一圈，我 28 天就走了一圈。到底谁快谁慢？”
关于上述对话，你有什么看法？
第三节
圆周运动
二、描述圆周运动的物理量
2
角速度 \(\omega \)
\omega = \frac{\varphi}{t}
3
周期 \(T \)
4
转速 \(n \)
做匀速圆周运动的物体运动一周所用的时间
单位：rad/s，读作弧度每秒
单位：s
单位：r/s，读作转每秒
单位时间沿圆周运动的圈数
第三节
圆周运动
二、描述圆周运动的物理量
角速度 \(\omega \)
\omega = \frac{\varphi}{t}
周期 \(T \)
转速 \(n \)
T = \frac {1}{n}
= \frac{2 \pi}{T} =2\pi n
2
3
4
v= \frac{s}{t}
线速度 \(v \)
= \frac{2 \pi r}{T}
1
\(\omega\)、\(T\)、\(n\) 之间只相差一个常量
第三节
圆周运动
三、线速度、角速度、周期之间的关系
1
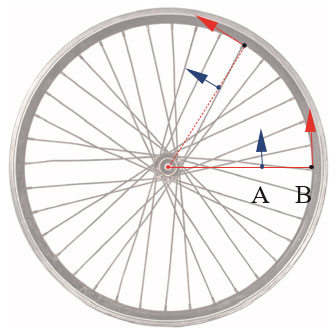
同轴转动
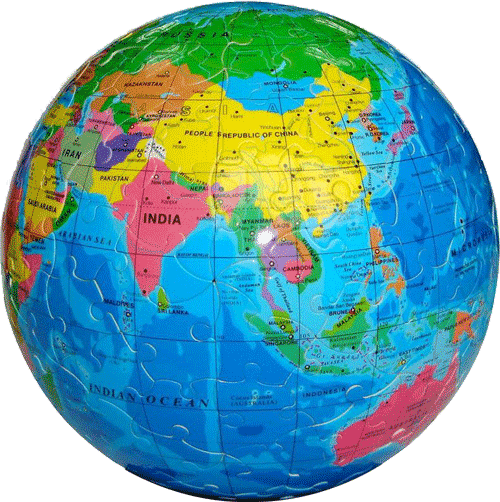
自转轴
广州
北京
同一转体 \(\omega \)、\(T\)、\(n\) 相同
离轴远（即 \(r\) 大）的质点 \(v\) 大
第三节
圆周运动
三、线速度、角速度、周期之间的关系
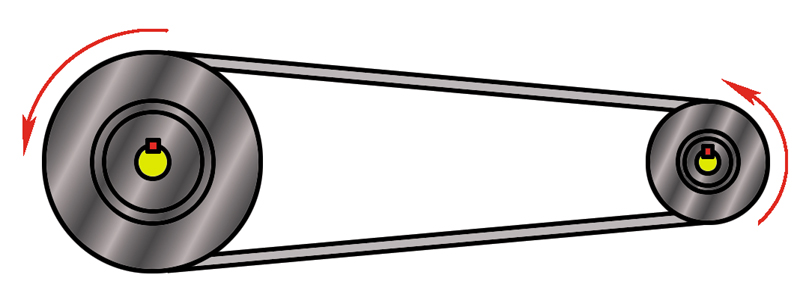
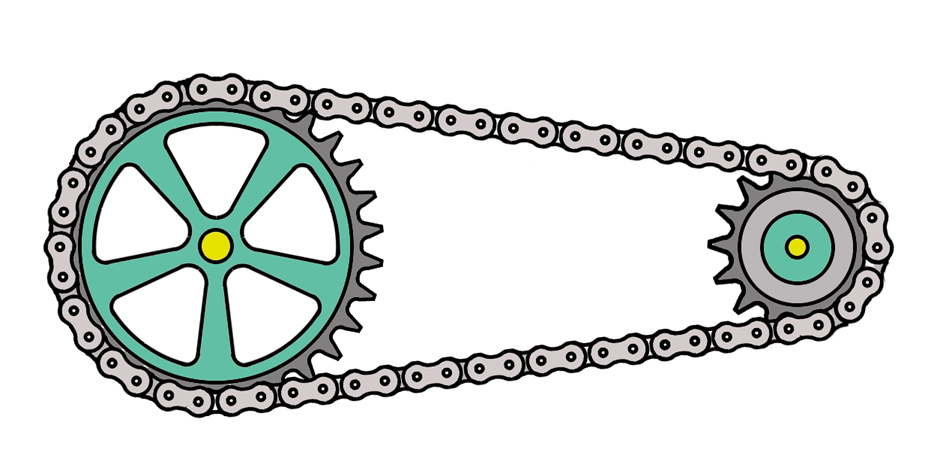
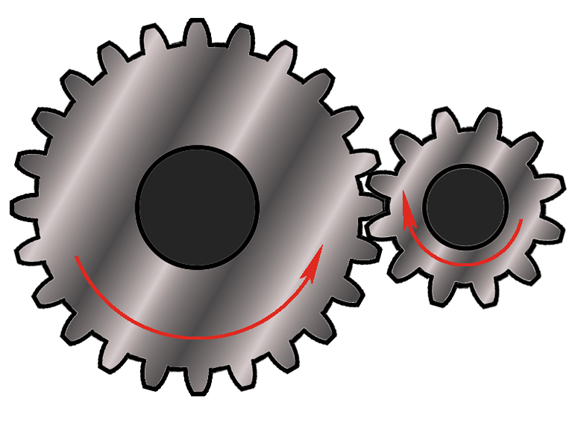
同一皮带（链条） \(v \) 相同
半径 \(r\) 大的转体 \(\omega\) 小
2
皮带、链条、齿轮传动
第三节
圆周运动
三、线速度、角速度、周期之间的关系
v= \frac{s}{t}
线速度 \(v \)
= \frac{2 \pi r}{T}
1
角速度 \(\omega \)
\omega = \frac{\varphi}{t}
周期 \(T \)
转速 \(n \)
T = \frac {1}{n}
= \frac{2 \pi}{T} =2\pi n
2
3
4
v={\omega}r
第三节
圆周运动
三、线速度、角速度、周期之间的关系
判断下列说法正确与否
由 \(v = {\omega}r\) 可知，半径 \(r\) 越大，线速度 \(v\) 也越大
由 \(v = {\omega}r\) 可知，线速度 \(v\) 与角速度 \(\omega\) 成正比
由 \(\omega = \frac{v}{r}\) 可知，角速度 \(\omega\) 与半径 \(r\) 成反比
线速度 \(v\) 越大，转速 \(n\) 一定越大
角速度 \(\omega\) 越小，转速 \(n\) 一定越大
第三节
圆周运动
三、线速度、角速度、周期之间的关系
A、B 两点分别位于大、小轮的边缘上，C 点位于大轮半径的中点，大轮的半径是小轮的 2 倍，它们之间靠摩擦传动，接触面上没有滑动。请在该装置的 A、B、C 三个点中选择有关的两个点，说明公式 \(v={\omega}r\) 的以下三种变量关系：
（1）\(v\) 相等，\(\omega \) 跟 \(r\) 成反比。
（2）\(\omega \) 相等，\(v\) 跟 \(r\) 成正比。
（3）\(r\) 相等，\(v\) 跟 \(\omega \) 成正比。
第三节
圆周运动
三、线速度、角速度、周期之间的关系
已知地球的半径 \( R = 6.37×10^3 \rm{km} \)，上海位于北纬 30° 附近。问：
（1）位于赤道上的物体随地球自转的角速度和线速度分别是多大？
（2）位于上海的物体随地球自转的线速度是多大？
第四节
向心力 向心加速度
第四节
向心力 向心加速度
一、物体做匀速圆周运动的条件
知识回顾：物体做曲线运动的条件
物体所受合力的方向与其速度方向不在一条直线上
\(v\)
\(v\)
\(G\)
\(G\)
第四节
向心力 向心加速度
一、物体做匀速圆周运动的条件
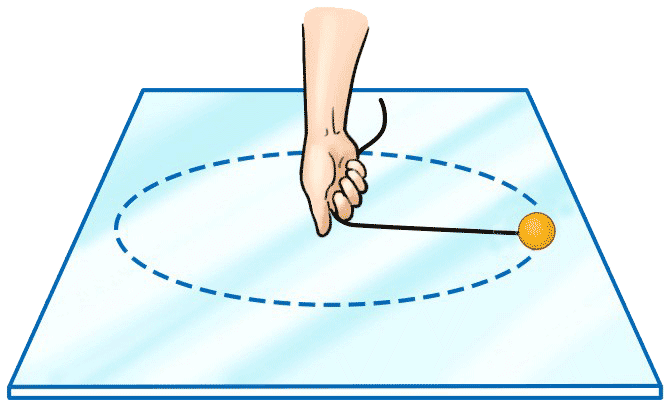
1
细绳的拉力的方向与小球的速度方向有什么关系？
\(T\)
\(v\)
2
将手松开，小球将做怎样的运动？
\(T\)⊥\(v\)
脱离圆周，沿切线方向飞出
物体做匀速圆周运动的条件是受到与物体的速度方向垂直、始终指向圆心的合力作用，这个力叫做向心力（centripetal force）。
第四节
向心力 向心加速度
一、物体做匀速圆周运动的条件
说出做匀速圆周运动的物体所受的向心力来源
\(T\)
\(T\)
\(N\)
\(G\)
弹力作为向心力
合外力作为向心力
摩擦力作为向心力
合外力作为向心力
\(f\)
\(N\)
\(G\)
第四节
向心力 向心加速度
一、物体做匀速圆周运动的条件
说出做匀速圆周运动的物体所受的向心力来源
重力和弹力的合力作为向心力
第四节
向心力 向心加速度
一、物体做匀速圆周运动的条件
物体做匀速圆周运动的条件是受到与物体的速度方向垂直、始终指向圆心的合力作用，这个力叫做向心力（centripetal force）。
向心力是根据作用效果命名的力，重力、弹力、摩擦力或者这些力的合力都可以作为向心力。向心力只改变速度的方向，不改变速度的大小。
知识回顾
力的分类
性质：重力、弹力、摩擦力
效果：拉力、压力、推力、支持力、阻力、向心力
第四节
向心力 向心加速度
二、向心力的大小与哪些因素有关？
\(T\)
\(T\)
\(N\)
\(G\)
猜想
向心力大小 \(F_向\)可能与圆周运动物体的
-
圆周半径（\( r \)）
-
运动快慢（\( \omega \)、\(T\)、\(n\)、\(v \)）
-
质量（\(m\)）
都有关。
第四节
向心力 向心加速度
二、向心力的大小与哪些因素有关？
探究向心力大小与半径、角速度、质量的关系
⑦电动机控制器（\(\omega\)）
②无线力传感器（\(F\)）
③砝码（\(m\)）
\(r\)
第四节
向心力 向心加速度
二、向心力的大小与哪些因素有关？
1
\(\omega\) 与 \(m\) 一定时，
| 实验序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| r/m | |||||
| F/N |
\(F \propto r\)
第四节
向心力 向心加速度
二、向心力的大小与哪些因素有关？
2
\(r\) 与 \(m\) 一定时，
| 实验序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| ω/(rad/s) | |||||
| F/N |
\(F \propto \omega ^2\)
F/N
\({\omega ^2}/{\rm{ra}}{{\rm{d}}^2} \cdot {{\rm{s}}^{ - 2}}\)
化曲为直
第四节
向心力 向心加速度
二、向心力的大小与哪些因素有关？
3
\(\omega\) 与 \(r\) 一定时，
| 实验序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| m/kg | |||||
| F/N |
\(F \propto m\)
第四节
向心力 向心加速度
二、向心力的大小与哪些因素有关？
\(F \propto m\)
\(F \propto r\)
\(F \propto \omega ^2\)
通过控制变量法得：
大量的研究表明，做匀速圆周运动物体受到的向心力 \(F\) 的大小等于物体的质量 \(m\)、圆周半径 \(r\) 和角速度 \(\omega\) 的二次方的乘积，即
F = m{\omega ^2}r
将 \(v = \omega r\) 代入上式，可得
F = m\frac{{{v^2}}}{r}
第四节
向心力 向心加速度
三、向心加速度
由牛顿第二定律：\(F=ma\)
匀速圆周运动的加速度叫做向心加速度，向心加速度只改变速度的方向，不改变速度的大小。
F = m{\omega ^2}r
F = m\frac{{{v^2}}}{r}
a = {\omega ^2}r
a = \frac{{{v^2}}}{r}
向心加速度大小不变，方向始终指向圆心
因此，匀速圆周运动是变加速曲线运动。
第五节
圆周运动的应用
第五节
圆周运动的应用
1、汽车在水平地面的转弯
如图，公路转弯处弯道半径 \(R\) ＝ 100 m，汽车的质量 \(m\) = 1 800 kg，\(g\) 取 10 \(\rm{m/s^2}\)。
（1）当汽车以 \(v_1 \) = 10 m/s 的速率行驶时，其所需的向心力为多大？
（2）若汽车轮胎与路面间的动摩擦因数 \(\mu \) = 0.4，且最大静摩擦力等于滑动摩擦力。若路面是水平的，问汽车转弯时不发生径向滑动（离心现象）所允许的最大速率 \(v_m\) 为多少 ？
P40/8
第五节
圆周运动的应用
2、离心现象
做圆周运动的物体，如果受到的力不足以提供所需的向心力，物体就会远离圆心，这就是离心现象。
脱水桶：衣物对水的附着力小于水需要的向心力
棉花糖：由于缺少足够的向心力，糖液无法维持圆周运动，从腔壁上的小孔飞出
第五节
圆周运动的应用
2、离心现象
载人离心机
飞行员的血液由于离心运动会流向下肢，造成飞行员大脑缺血，感觉四肢沉重，这种现象叫做过荷
第五节
圆周运动的应用
2、离心现象
试解释下列常见现象。
（1）舞蹈演员在表演旋转动作时，裙子会张开。
（2）在雨中转动伞柄，伞面上的雨水会很容易被甩掉。
（3）满载黄沙的卡车急转弯时，部分黄沙会被甩出。
第五节
圆周运动的应用
3、火车的转弯
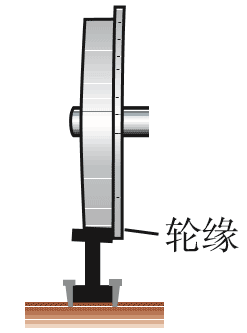
火车的车轮上有突出的轮缘
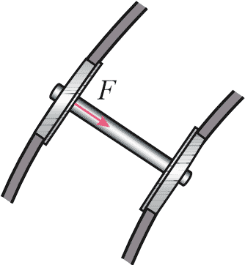
如果铁路弯道的内外轨一样高，火车转弯时，外侧车轮的轮缘挤压外轨。但是，火车质量太大，靠这种办法得到向心力，将会使轮缘与外轨间的相互作用力过大，不仅铁轨和车轮极易受损，还可能使火车侧翻。
弯道处使外轨略高于内轨
第五节
圆周运动的应用
3、火车的转弯
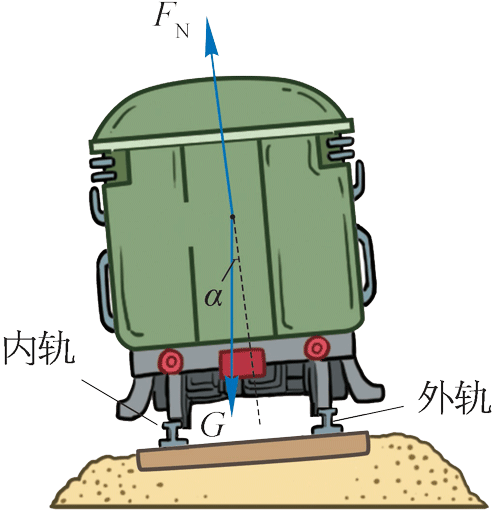
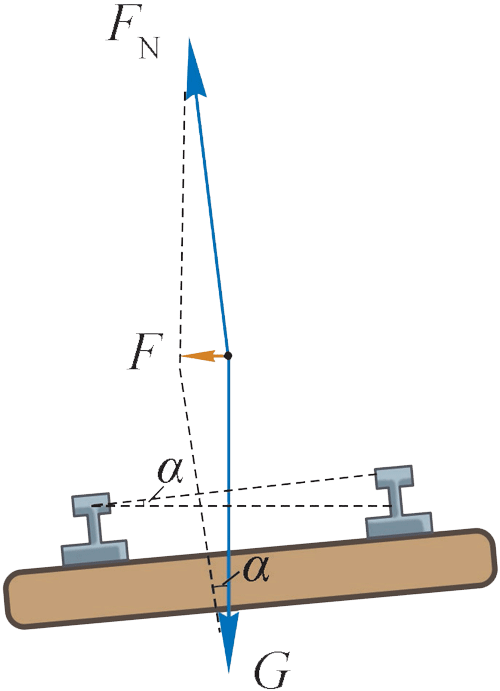
火车受到的支持力 \(F_N\) 与重力 \(G\) 的合力 \(F\) 沿水平方向，提供了火车转弯所需的向心力。
第五节
圆周运动的应用
3、火车的转弯
已知我国高铁的轨道间距为 1.5 m，一辆高铁列车要通过半径为 5 625 m 的弯道，且该弯道外轨比内轨高 15 cm（角度较小时可认为 \(\tan \theta \) = \(\sin \theta \)），\( g \) 取 \(10 \rm{m/s^2}\)，高铁在通过此弯道时的最佳的安全速度约为（ ）
A．80 m/s B．75 m/s C．70 m/s D．65 m/s
P40/7
第五节
圆周运动的应用
4、圆锥摆
如图，一条长为 \(L\) 的轻绳的上端固定，下端栓一质量为 \(m\) 的小球，给小球一个初速度使它在水平面内做匀速圆周运动。若绳与竖直方向的夹角为 \(θ\)，求小球所受的向心力大小及其线速度大小 。
P30/10
第五节
圆周运动的应用
4、圆锥摆
如图，两个质量相同的小球用长度不等的细线拴在同一点，并在同一水平面内做同方向的匀速圆周运动，则它们的（ ）
A．角速度相同 B．周期不同
C．线速度大小相同 D．向心力大小相同
P46/31
第五节
圆周运动的应用
4、圆锥摆——旋转飞椅
质量为 \(m\) 的旋转飞椅在水平面内做匀速圆周运动，圆盘半径为 \(R\)，绳索长度为 \(L\)，与竖直方向夹角为 \(\theta\)，求飞椅的转速 \(n\)。
第五节
圆周运动的应用
5、汽车过拱形桥、凹形路面
假设有一质量为 800 kg 的小车驶上圆弧半径为 50 m 的拱桥。g 取 10 \(\rm{m/s^2}\)，求：
（1）小车到达桥顶时速度为 5 m/s，小车对桥的压力是多大？
（2）小车以多大速度经过桥顶时恰好腾空，对桥没有压力？
（3）小车对地面的压力过小是不安全的。从这个角度讲，小车过桥时的速度不能过大。对于同样的车速，拱桥圆弧的半径大些比较安全，还是小些比较安全 ？
P32/10
第五节
圆周运动的应用
5、汽车过拱形桥、凹形路面
如图，飞机由俯冲转为拉升的一段轨迹可看成一段圆弧，飞机做俯冲拉升运动时，在最低点附近做半径 r＝180 m 的圆周运动，如果飞行员的质量为 60 kg，飞机经过最低点 P 时的速度为 120 m/s，g 取 10 \(\rm{m/s^2}\)，则这时飞行员对座椅的压力大小为_______________N，方向 _________。飞行员处于_____________（选填“超重”或“失重”）状态。
P32/10
第五节
圆周运动的应用
6、测定分子（子弹）速率
1920年，美国物理学家史特恩（O．Stern，1888－1968）提出了一种应用圆周运动规律测定气体分子速率的方法。史特恩实验装置如图所示。A、B 为双层共轴圆筒形容器，内筒 A 半径为 r，外筒B半径为 R，内外筒可同时绕转轴 K 以同一角速度高速旋转；容器内部抽成高度真空，沿转轴 K 装有一根镀银的铂丝，铂丝通电加热使银蒸发成气体，一些银原子穿过筒 A 的狭缝 a 射出，最终落于筒 B 的内表面。由于银原子由内筒运动到外筒需要一定时间，若容器不动，这些原子将到达外筒内壁上的 b 点；若容器以角速度 ω 旋转，这些原子将到达外筒内壁上的 bʹ 点。
第五节
圆周运动的应用
6、测定分子（子弹）速率
为了测定子弹的飞行速度，在一根水平放置的轴杆上固定两个薄圆盘 A、B，盘 A、B 平行且相距 \(l\) ＝ 2 m，轴杆的转速 n = 3 600 r/min。子弹穿过两盘留下两弹孔 a、b，测得两弹孔所在半径的夹角 θ ＝ 30°，如图。则该子弹的速度可能是（ ）
A．360 m/s B．720 m/s C．1 440 m/s D．108 m/s
P41/4
第五节
圆周运动的应用
6、测定分子（子弹）速率
如图所示是一种可用于测定子弹速度的装置示意图，纸质圆筒绕中心轴 OOʹ 以角速度 \(\omega\) 旋转，子弹以一定速度沿与轴线平行的方向从圆筒一个底面上的 A 点射入，从另一个底面上的 B 点射出，射出时 A、B 两点在圆筒上的位置如图中所示。若 A 点与 B 点所在半径的夹角为 \(\theta\)，圆筒的长度为 \(l\)，求子弹的速度大小 \(v\)。
课本P27/5
第五节
圆周运动的应用
6、测定分子（子弹）速率
用如图（a）所示的装置可以测定分子速率。在小炉 O 中，金属银熔化并蒸发。银原子束通过小炉的圆孔逸出，经过狭缝 \(\rm{S}_1\) 和 \(\rm{S}_2\) 进入真空的圆筒 C。圆筒 C 可绕过 A 点且垂直于纸面的轴以一定的角速度转动。
（1）若已测出圆筒 C 的直径为 \(d\)、转动的角速度为 ω，银原子落在玻璃板 G 上的位置到 b 点的弧长为 s，写出银原子速率的表达式；
课本P31/9
第五章 曲线运动
By fjphysics
