
高中物理——绪论课

什么是物理学?
物理学研究的是物质的最普遍的运动形式和物质的基本结构,它是其他自然科学的基础。

为什么要学物理?
三、物理学改变了世界
第一次突破:牛顿力学的建立和热力学的发展。导致了蒸汽机的发明,使人类进入了蒸汽动力时代,引发了第一次工业革命。
瓦特的改良蒸汽机
斯蒂芬逊的蒸汽机车


三、物理学改变了世界
第二次突破:19世纪,法拉第发现了电磁感应现象,麦克斯韦创立了电磁理论,推动了电机、电器、电信设备等的发明和制造,使人类进入了电气时代。


法拉第在给公众做科普讲座
马可尼和他的无线电器械
三、物理学改变了世界
第三次突破:20世纪以来,根据相对论、量子力学,大力开发新材料、新光源、新能源,发展了微电子技术、计算机技术,使人类进入了信息时代。


秦山核电站
互联网
四、高中物理与初中物理的区别
高中物理的知识面更广,内容更丰富,更深入
初中物理较多的是定性的描述,高中物理则有较多的定量计算。
初中物理以现象为主,比较直观,高中物理则要透过现象看本质,有一定的抽象思维要求。


五、怎样学好高中物理
多看:调动我们的感官去搜寻事实、数据,观察现象的变化过程,并做好记录。
五、怎样学好高中物理
多动:勤于实践,多动手操作,除了努力完成课本中规定的各种体验、实验、操作之外,还要设法完成课外实验、课题研究,特别要重视亲身体验和经历。
五、怎样学好高中物理
多想:要善于运用分析、推理和建立物理情景等方法去解决问题,掌握知识的来龙去脉。

巴甫洛夫讲述的故事
夜深了,一位巴格达商人走在黑漆漆的山路上。突然,有个声音传来:“弯下腰,请多捡些小石子,明天会有用的!”

商人决定执行这一指令,弯腰捡起几颗石子。到了第二天,当商人从袋中掏出“石子”看时,却惊奇地发现。原来那都是一块块亮晶晶的宝石!他后悔莫及,天哪!昨晚我为什么不多捡些呢?
巴甫洛夫讲完故事后说:
教育就是这么回事,当我们长大成人之后,才会发现以前学的科学知识是珍贵的宝石,但同时也会觉得可惜,我们学得太少了!
第一章 A.质点 位移和时间
一、质点
在某些条件下,把整个物体看作一个有质量的点,这种用来代替物体,有质量的点叫做质点。

什么条件下,可以将一个物体看做质点?
- 物体各个点的运动状况相同(物体不发生转动)
- 物体的形状,大小与所研究的运动无关。(物体的大小远远小于研究的尺度)
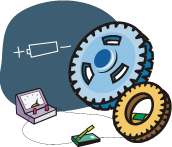
物理学中的“质点”是一种理想化模型,研究下列物体的运动时可视为质点的是( )
(A)研究运动员跳高的过杆
(B)研究车轮边缘的速度
(C)计算轮船在海洋中的航行速度
(D)研究乒乓球的接发球技术
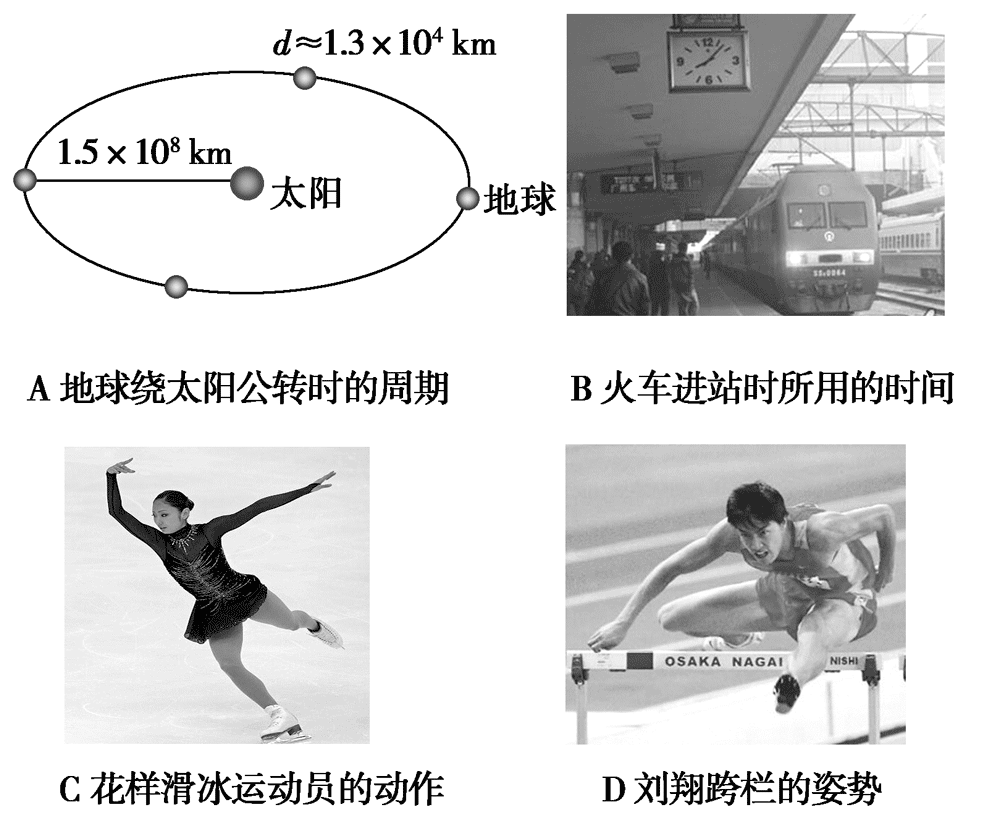
在研究以下四种情况中提出的问题时,所涉及到的对象可看作质点的是( )
A
末位置
初位置
如图所示的圆形大花坛,其道路半径为r,甲、乙两人均从A抵达B,甲沿直径走,乙绕半圆弧走,他们的位移和路程各是多少?
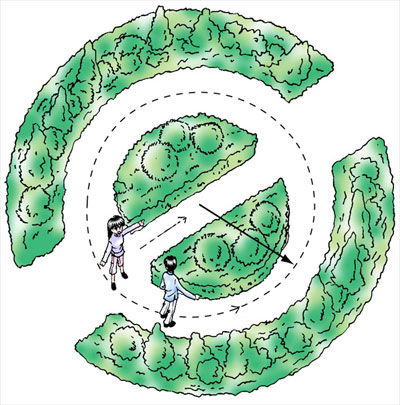
甲
乙
B
A
如图所示,坐标系中质点从A经O至B,质点的位移和路程分别为多少?请用有向线段画出A至B的位移。
s/cm
A
B
O
10
0
18
什么情况下路程等于位移
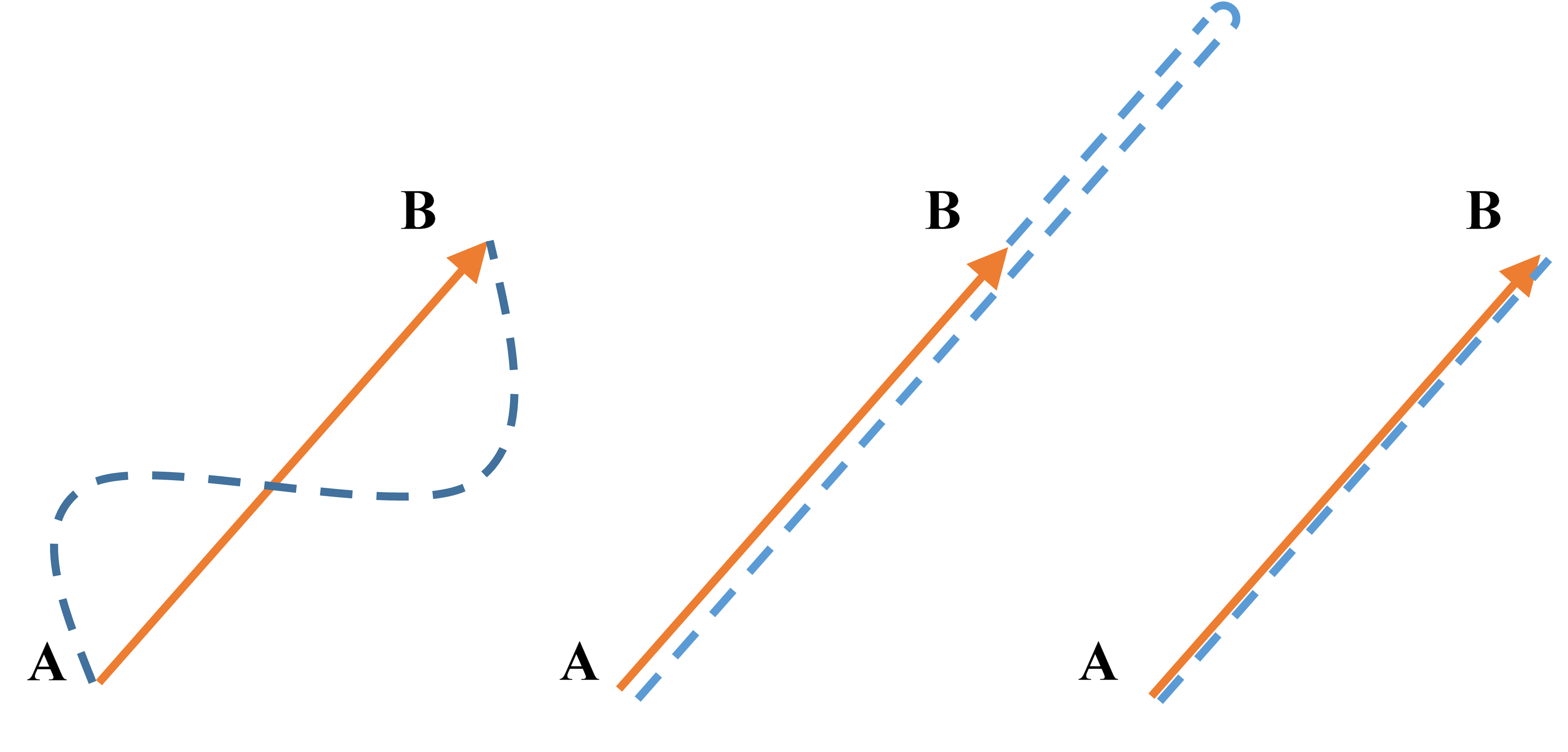
的大小?
市八中学作息时间表
| 节次 | 时间 |
|---|---|
| 升旗、早操 | 7:20-7:45 |
| 1 | 7:45-8:25 |
| 2 | 8:40-9:20 |
| 3 | 9:30-10:10 |
| 眼保健操 | 10:20-10:25 |
| 4 | 10:25-11:05 |
| 5 | 11:15-11:55 |
| 午休 | |
| 6 | 13:00-13:40 |
| 7 | 13:50-14:30 |
| 眼保健操 | 14:45-14:50 |
| 8 | 14:50-15:30 |
| 9 | 15:40-16:20 |
列车 时刻表

如图所示的时间轴。
(1)t2表示_______,称为___________________。
(2)t2~t3表示_______,称为___________。
(3)t0~t2表示_______,称为___________。
(4)tn-1~tn表示_______,称为_________。

时刻
时间
时间
时间
第3 s内
前2 s内
第n s内
第2 s末或第3 s初
第一章 B 匀速直线运动的图像
自动记录仪
| t/s | 0 | 1 | 2 | 3 | 4 |
| s/m | 0 | 5 | -4 | -1 | -7 |
s /m
t /s
-4
-2
6
4
0
4
2
2
1
3
-6
试说出以下图线的速度(斜率)
一质点的s-t图如图所示,根据这个图像可以得知质点在前5 s内做__________运动,速度为_______,质点在前4 s内的位移为______,质点在第4 s内的位移为_______,通过5 m位移所需的时间_______。
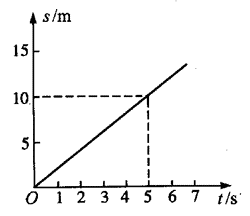
匀速直线
8 m
2 m/s
2 m
2.5 s
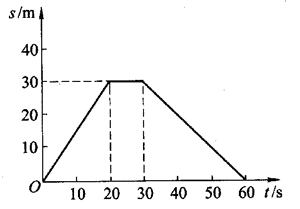
如图是一物体运动的s-t图,根据图像可知:
(1)在0~20 s这段时间内,物体以______m/s的速度做匀速直线运动。
(2)在20~30 s这段时间内,物体运动的路程是_____m。
1.5
0
如图是一物体运动的s-t图,根据图像可知:
(3)在30~60 s这段时间内物体运动的方向为__________________,路程为_______m。
(4)在整个运动过程中物体经过的路程为_______m,离出发点的最大距离为________m。

与初速方向相反
30
60
30
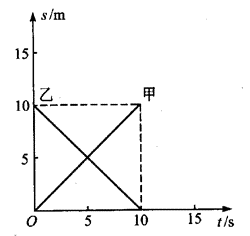
甲、乙两物体在同一直线上运动,运动情况如图所示。下列说法中正确的是( )
(A)经过2.5 s时间,甲、乙两物体相遇
(B)经过5 s时间,甲物体达到乙物体的出发点
(C)甲、乙两物体速度大小相等,方向相反
(D)接近10 s时,乙物体的速度接近零
5
10
-1 m/s
第一章 C 快慢变化的运动
平均速度和瞬时速度
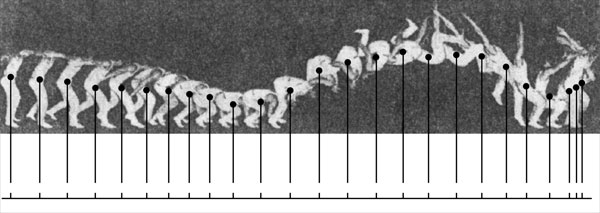
重心的投影在做直线运动
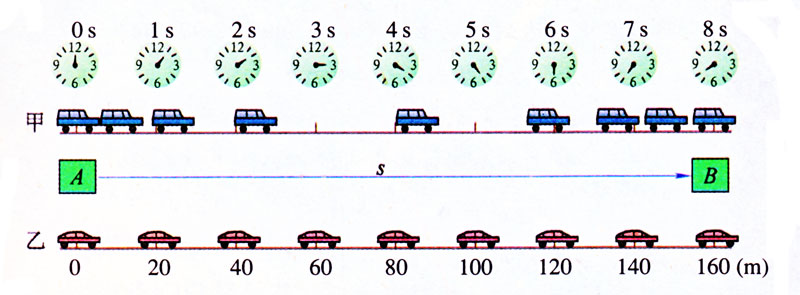
甲车的平均快慢与乙车的快慢相同
等效替代

某位置(或某时刻)的瞬时速度,就是无限逼近该位置(或该时刻)附近的位移(或时间)内的平均速度
6.物体在某时刻的瞬时速度是5 m/s,它的意思是(D)
(A)物体在该时刻前1 s内通过的位移是5 m
(B)物体在该时刻后的1 s内通过的位移是5 m
(C)物体在该时刻后每秒钟通过的位移都是5 m
(D)若物体从该时刻做匀速直线运动,它在每秒钟内通过的位移都是5 m
4.下列描述的速度中,属于平均速度的是②③⑤⑦,属于瞬时速度的是①④⑥。(均选填序号)
①鱼雷以790 m/s的速度击中目标;
②汽车通过站牌时的速度是72 km/h;
③信号沿动物神经传播的速度大约为100 m/s;
④在市区某段对汽车限速,不得超过60 km/h;
⑤台风以36 m/s的速度向东北方向移动;
⑥子弹以900 m/s的速度从枪口射出;
⑦出租车的行驶速度是36 km/h。
7.关于匀速直线运动,下列说法中,正确的是(B)
(A)速率不变的运动,一定是匀速直线运动
(B)瞬时速度不变的运动,一定是匀速直线运动
(C)相同时间内平均速度相同的运动,一定是匀速直线运动
(D)瞬时速度的方向始终不变的运动,一定是匀速直线运动
8.下列关于瞬时速度和平均速度的说法中,正确的是( B )
(A)变速直线运动中一段时间内的平均速度一定不等于它某一时刻的瞬时速度
(B)匀速直线运动中物体任意一段时间内的平均速度都等于它任一时刻的瞬时速度
(C)若物体在某段时间内的平均速度等于零,则它在这段时间内任一时刻的瞬时速度一定等于零
(D)若物体在某段时间内任一时刻的瞬时速度都等于零,则它在这段时间内的平均速度不一定等于零
9.如图,甲、乙两辆汽车同时同地出发,沿平直公路运动,由s-t图可知,t时刻甲、乙两车在同一点相遇。下列说法中,正确的是( C )
(A)t时刻,甲、乙两车的瞬时速度相等
(B)在t时间内,甲、乙两车平均速率相等
(C)在t时间内,甲、乙两车平均速度相等
(D)t时间内,甲车平均速度大于乙车平均速度
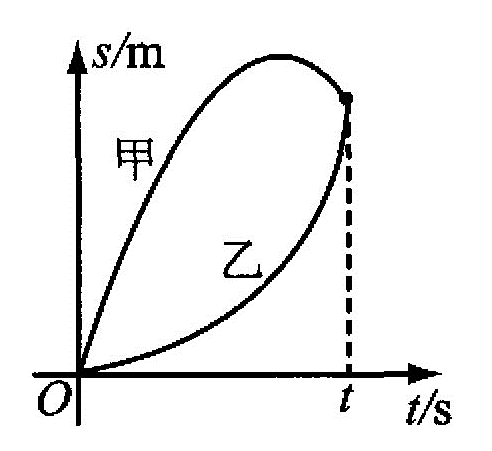
第一章 D 现代实验技术—数字化信息系统
1、DIS实验
数字化信息系统——Digital Information System


皮尺
超声波测距仪
Google无人车

激光测距仪

1、DIS实验
计算机系统描绘出精细的3D地形图
2、DIS的基本结构
传感器
数据采集器
计算机






位移传感器
电压传感器
电流传感器
力传感器

光电门传感器
3、练习使用传感器
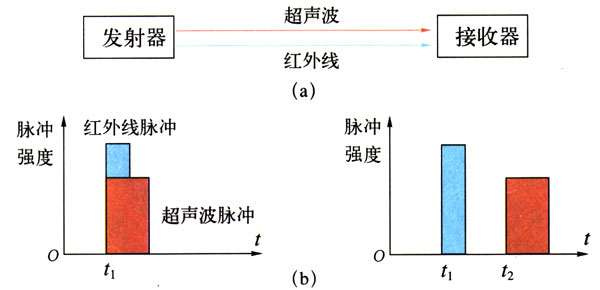
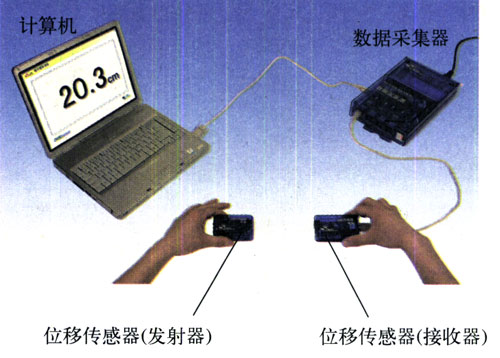
位移传感器测距离的原理
3、练习使用传感器
位移传感器

位移传感器(接收器)
位移传感器(发射器)

红外线
超声波
3、练习使用传感器


4、用DIS研究变速运动的s-t图
计算机
小车
轨道
位移传感器(发射器)
位移传感器(接收器)
数据采集器
位移传感器的发射器固定在小车上,接收器固定在轨道一端。
导轨调节成倾斜状态。
4、用DIS研究变速运动的s-t图

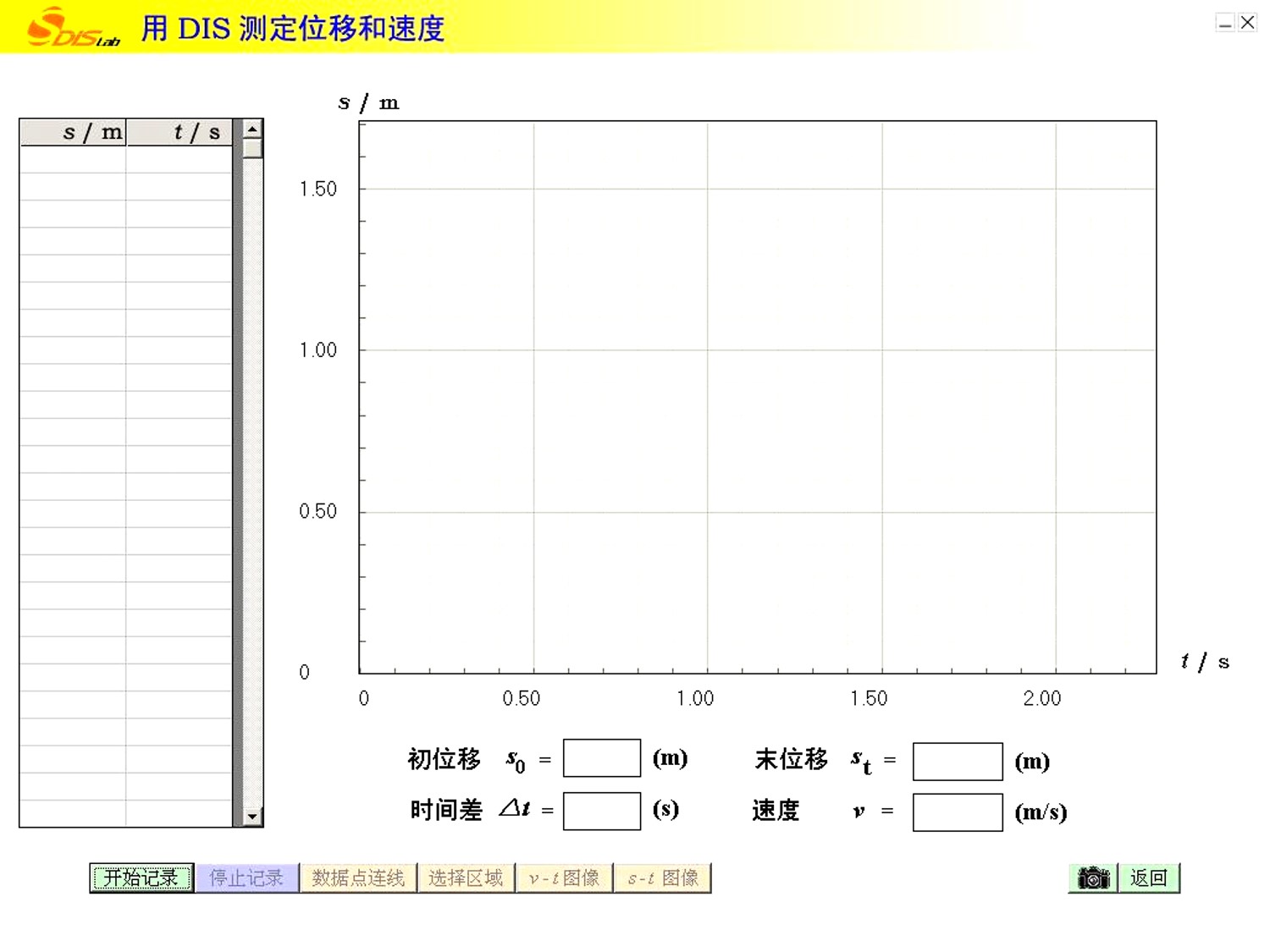
数据
显示区
测量值
图像显示区
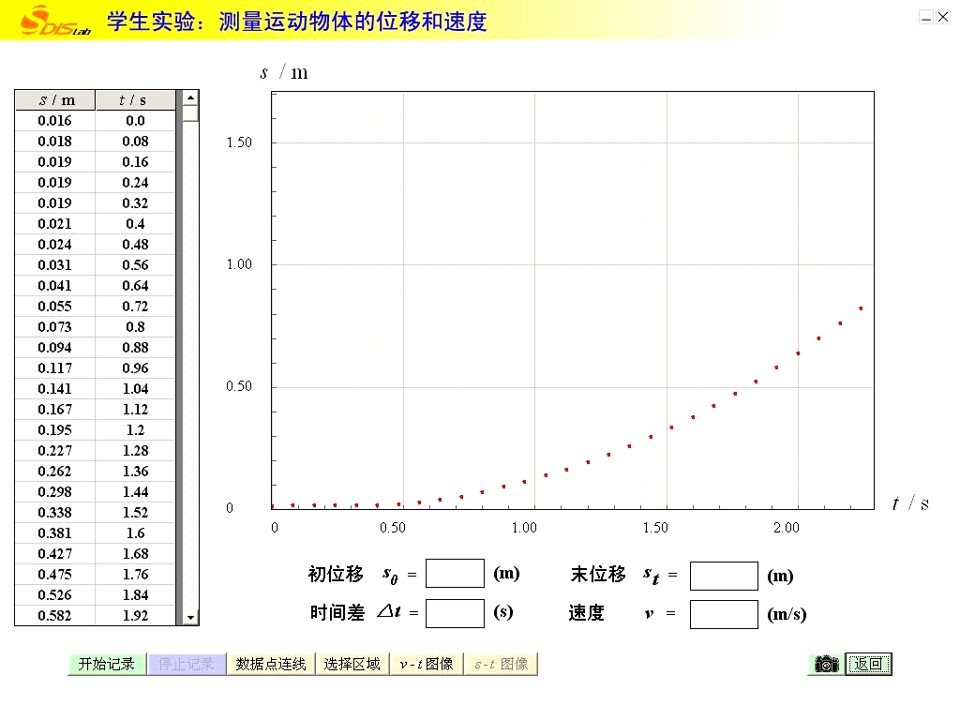
采集数据
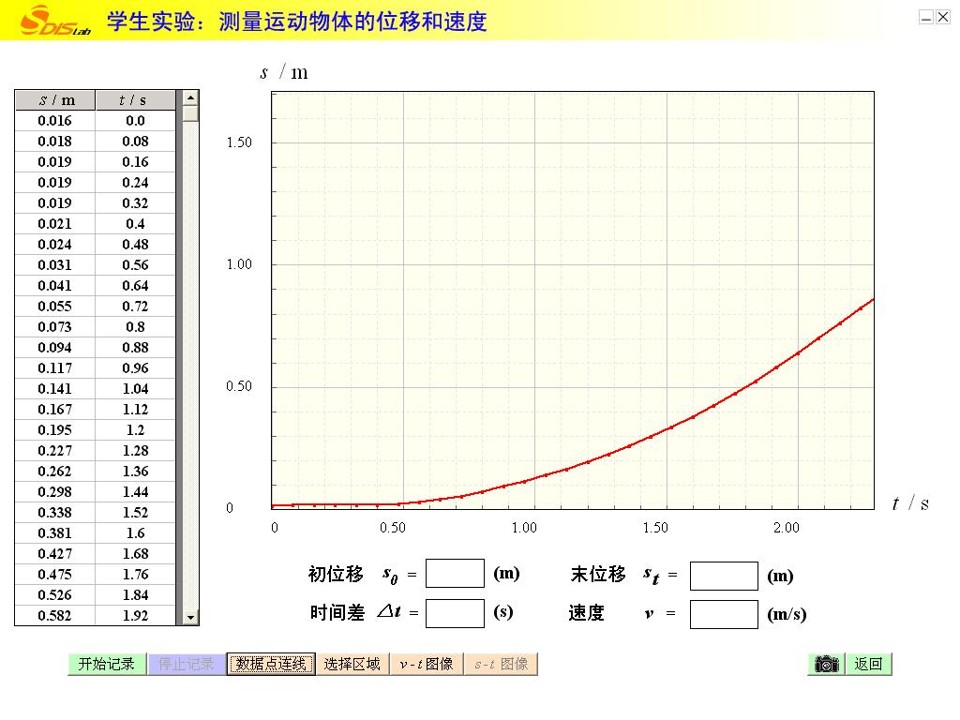
数据点连线
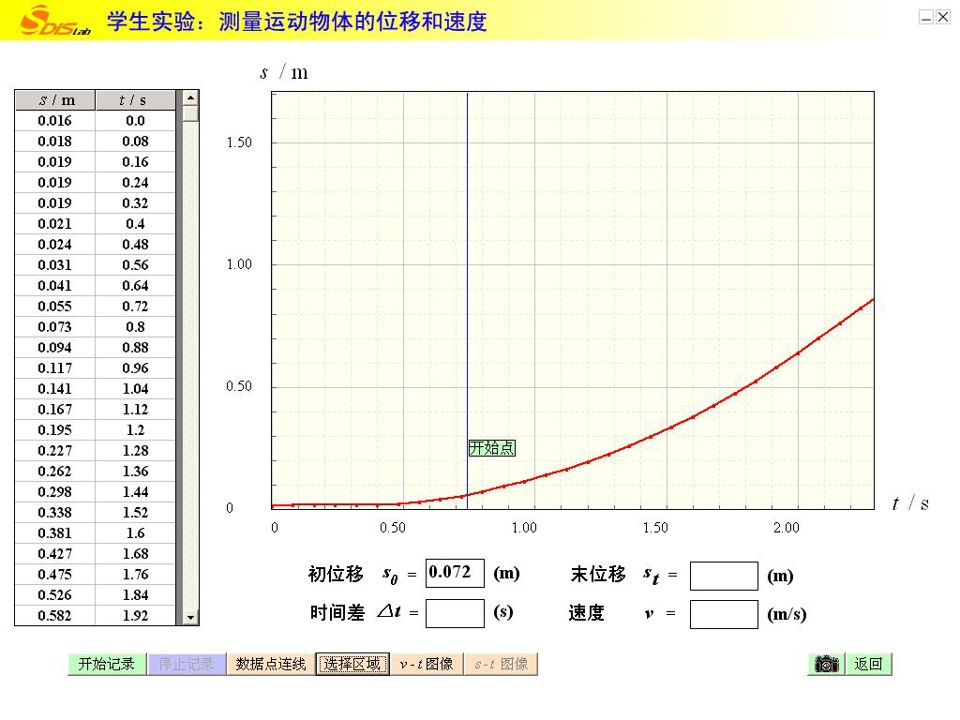
5、用DIS测变速直线运动的平均速度
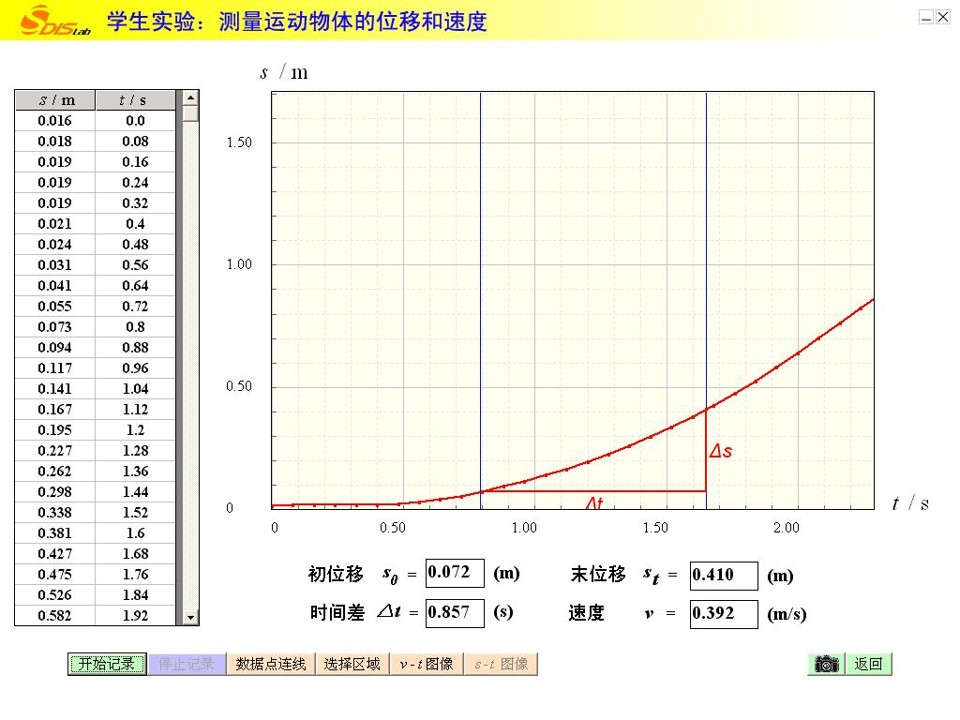
选择区域
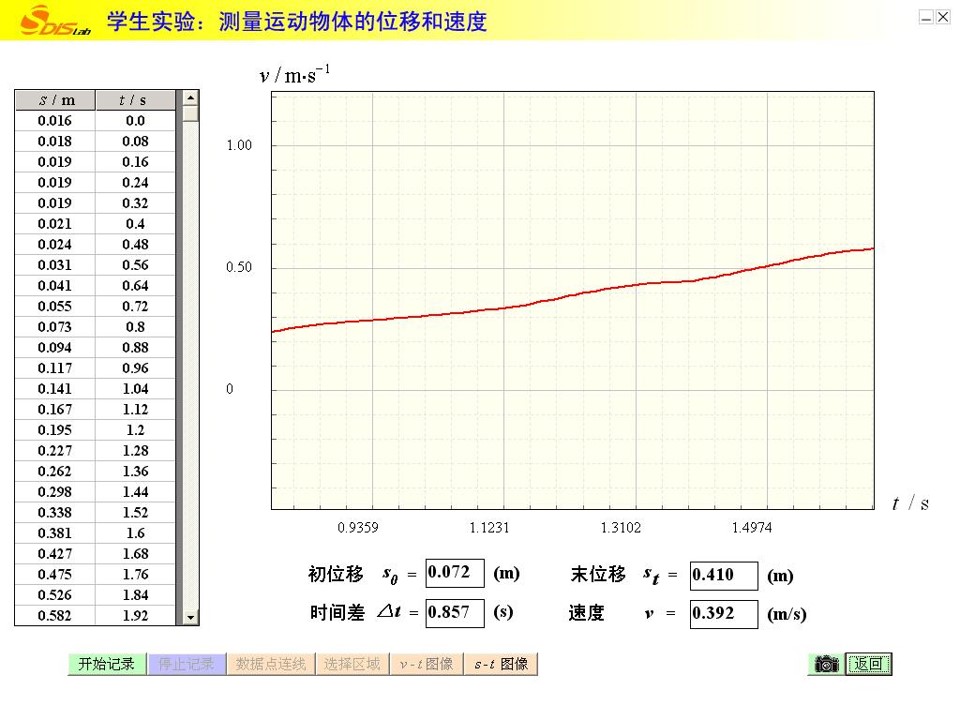
v-t图像
6、用DIS测变速直线运动的瞬时速度
光电门传感器

光电门测量瞬时速度的原理

红外线
6、用DIS测变速直线运动的瞬时速度
测量的是挡光时间\(\Delta t\)
若再给出挡光片的宽度\(d\)
则可以计算出速度\(v=\frac{d}{\Delta t}\)

换用不同宽度的挡光片做4次
注意:每次释放小车的位置应相同
6、用DIS测变速直线运动的瞬时速度
6cm
4cm
8cm
6、用DIS测变速直线运动的瞬时速度
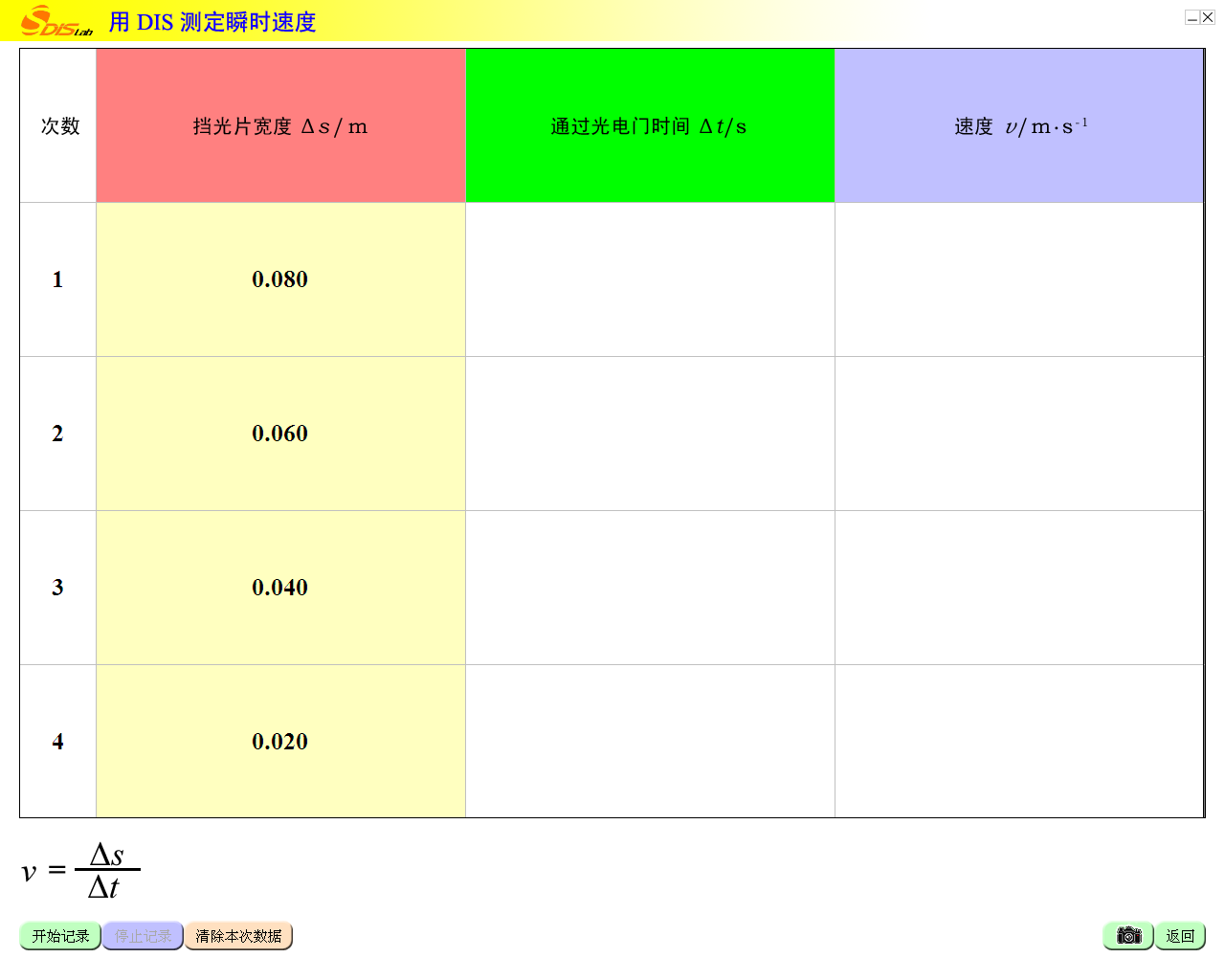
挡光片的宽度逐渐减小时,测得的速度值越来越趋近于小车经过挡光片所在位置的瞬时速度。
结论
11.在用位移传感器测直线距离的实验中,改变接收器和发射器的相对距离是为了(D)
A.使实验更有趣 B.使实验做得更精确
C.多次测量求平均值 D.测量其可测的最大距离和最小距离
12.下列有关用位移传感器测直线距离的实验步骤中,不需要的操作是(D)
A.连接数据采集器与计算机
B.开启电源,运行DIS应用软件
C.改变接收器和发射器的相对距离
D.将小车放在一木板上,并将木板一端稍微垫高

5.在用传感器做实验时,下列说法正确的是( D )
A.位移传感器的发射器发射孔不必对准接收器的信号接收孔
B.光电门传感器实际测量的是物体通过挡光孔的速度
C.位移传感器连到数据采集器上的是发射器部分
D.用位移传感器做实验前,必须先打开发射器的电源开关
2.下列说法中正确的是(D )
(A)矢量的大小叫做标量
(B)位移的大小叫做路程
(C)平均速度的大小叫做平均速率
(D)瞬时速度的大小叫做瞬时速率
9.物体沿直线从A点经B点运动到C点,在AB段运动速度为60m/s,在BC段运动速度为30 m/s,且AB=3BC,则AC段中平均速度大小为( C)。
(A)37.5 m/s (B)45 m/s (C)48 m/s (D)52.5 m/s
设AB间距离为3s,BC间距离为s
10.关于瞬时速度和平均速度的理解,下列说法正确的是( B)
①瞬时速度为零,平均速度一定为零②瞬时速度为零,平均速度可以不为零③瞬时速度不为零,平均速度一定不为零④瞬时速度不为零,平均速度可以为零
(A)①③ (B)②④ (C)①④ (D)②③
11.如图所示为甲、乙、丙、丁四物体做直线运动的位移-时间图像。则在0~\(t_1\)时间内(C )。
(A)丁的位移最大 (B)四者位移不同
(C)甲、丁的路程相等 (D)丙的路程比乙大
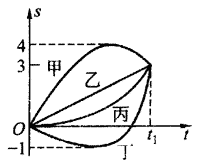
s-t图像并不是物体运动的实际轨迹
12.物体在A、B两地沿直线做往返运动。设A到B的平均速率为\(v_1\),由B到A的平均速率为\(v_2\),物体往返一次,平均速度的大小与平均速率分别是( A )
(A)0,\(\frac {2v_1v_2}{v_1+v_2}\)(B)0,\(\frac {v_1+v_2}{2}\)
(C)均为\(\frac {2v_1v_2}{v_1+v_2}\) (D)均为0
设AB间距离为s

雷雨天,某同学从看到闪电到听到雷声大约经过3秒,已知光的传播速度 \( c = 3 \times {10^8}{\rm{m/s}} \),声音的传播速度\( v = 340{\rm{m/s}} \),则雷电发生处到该同学处的距离大约是多少?
已知红外线传播速度 \( c = 3 \times {10^8}{\rm{m/s}} \),超声波传播速度\( v = 340{\rm{m/s}} \),接收器接收到两种信号的时间差\( \Delta t = 0.001{\rm{s}} \) ,求物体位移。
第一章 E 速度变化的快慢
加速度

怎样描述物体速度变化的快慢
火箭发射时
10s内速度能增到约100m/s
万吨货轮起航
10s内速度增到0.2m/s
问题:火箭与货轮谁的速度变化大?谁的速度变化快?


加速度
1
蜻蜓起飞时
在0.8s内可达到8m/s
刘翔起跑时
在0.16内达到8m/s
问题:蜻蜓与刘翔谁的速度变化大?谁的速度变化快?


怎样描述物体速度变化的快慢
加速度
1
法拉利赛车起动时在7 s内可达到70 m/s
台风战斗机起飞过程中可在30 s内达到150 m/s
问题:法拉利与战斗机谁的速度变化快?

怎样描述物体速度变化的快慢
加速度
1
加速度
1
描述物体速度变化快慢的物理量
描述物体位置变化快慢的物理量
太阳帆

加速度
1
加速度
1
\(v\)(速度)与\(a\)的大小关系
v大a也大吗?
v为零a也为零吗?
否,汽车由静止启动瞬间
否,飞机高速匀速飞行
目前还有疑问?
a变大v也变大吗?
加速度
1
\(\Delta v\)(速度变化量)与\(a\)的大小关系
\(\Delta v\)大a也大吗?
\(\Delta v\)为零a也为零吗?
否,还与\(\Delta t\)有关
是
加速度
1
\(\frac{\Delta v}{\Delta t}\)(速度变化率)与\(a\)的大小关系
\(\frac{\Delta v}{\Delta t}\)大a也大吗?
速度变化越快,a也越大吗?
速度变化率大,a也大吗?
是
是
是
\(\frac{\Delta v}{\Delta t}\)(速度变化率、速度变化快慢)就是\(a\)
6.关于加速度的概念,下列说法正确的是( C )
(A)加速度就是增加的速度 (B)加速度仅反映了速度变化的大小
(C)加速度就是物体速度的变化率 (D)加速度反映了物体运动的快慢程度
7.下列说法中,错误的是( A )
(A)物体速度不变化,而加速度可以变化很大
(B)物体速度变化很大,而加速度变化不一定很大
(C)物体某一时刻的速度很大,而加速度可以等于零
(D)物体某一时刻速度等于零,而加速度可以不等于零
8.关于速度和加速度的关系,下列说法正确的有( D )
(A)加速度越大,速度越大 (B)速度越小,加速度也越小
(C)速度变化量越大,加速度也越大 (D)速度变化越快,加速度越大
6.下列说法中的“快”,指加速度较大的是( C )
(A)从高速公路走,很快就能到
(B)刘翔的起跑是比赛选手中最快的
(C)运用ABS新技术,汽车能很快停下来
(D)“神舟十一号”绕地球运动得很快
7.下列关于速度和加速度的说法中,正确的是( C )
(A)加速度表示速度变化的大小
(B)物体的速度为零,加速度也一定为零
(C)运动物体的加速度越来越小,表示速度变化越来越慢
(D)运动物体的加速度越来越小,表示物体运动的速度也越来越小
8.关于速度、速度改变量、加速度,正确的说法是( C )
(A)某时刻物体的加速度为零,其速度也为零
(B)加速度很大时,运动物体的速度一定很快变大
(C)速度很大的物体,其加速度可以很小,也可以为零
(D)物体运动的速度改变量越大,它的加速度一定越大
加速度的测量
2

计算机
小车
轨道
位移传感器(发射器)
位移传感器(接收器)
数据采集器
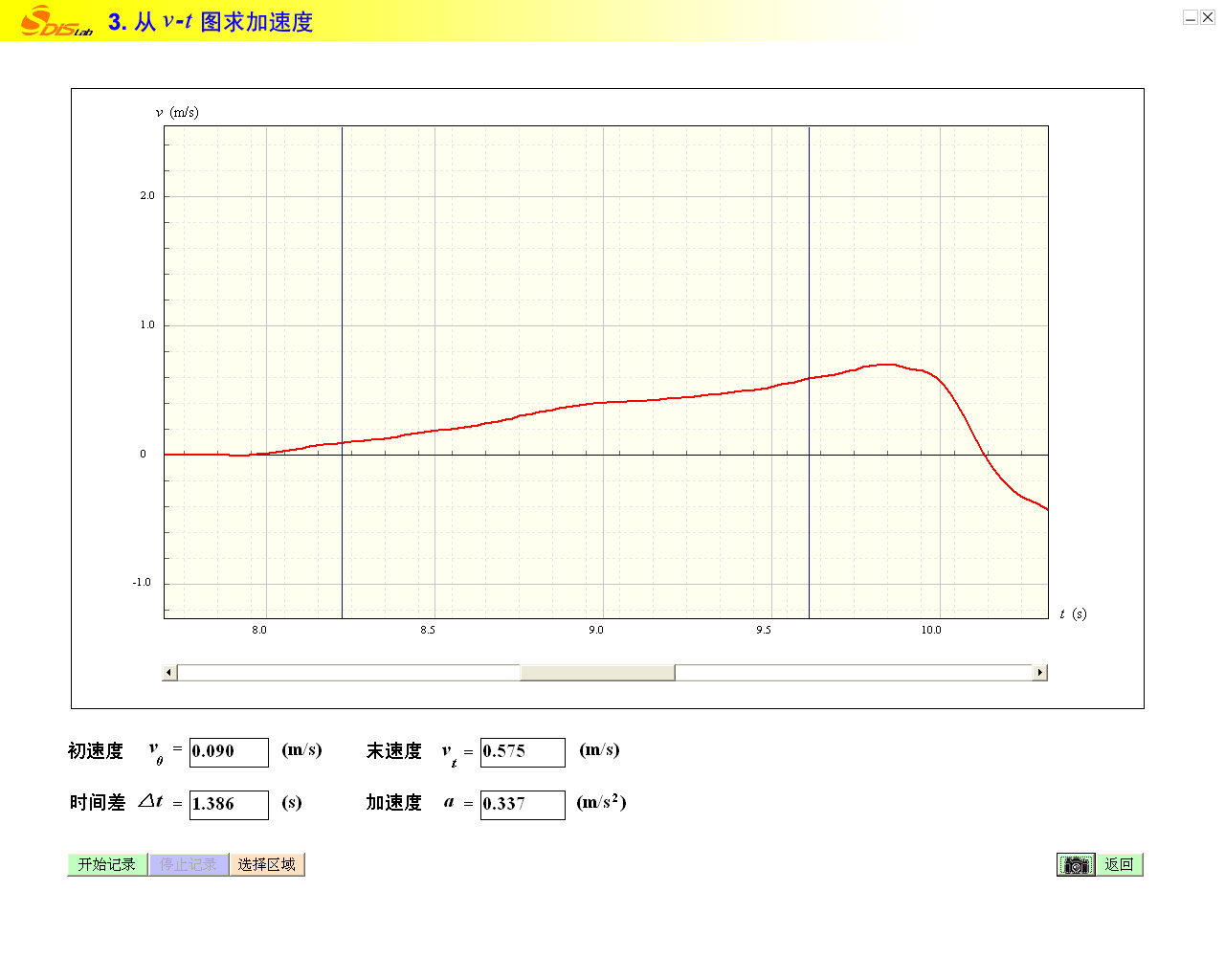
加速度的测量
2
v-t图像的斜率即加速度
4.质点从静止开始做直线运动,经5 s后速度达到10 m/s,这一过程中的加速度为2m/s2;然后匀速运动了20 s,这一过程中的加速度为0m/s2,最后经2 s后静止,这一过程中的加速度为-5m/s2。
加速运动时 \(\Delta v\)=______\(\rm m/s\) \(a\)=2\(\rm m/s^2\)
匀速运动时 \(\Delta v\)=______\(\rm m/s\) \(a\)=0\(\rm m/s^2\)
减速运动时 \(\Delta v\)=______\(\rm m/s\) \(a\)=-5\(\rm m/s^2\)
v一直为正
结论:\(\Delta v\)的符号(方向)必和\(a\)的符号(方向)相同
\(v\)(速度)与\(a\)的方向关系
v为正a也为正吗?
否,减速时两者符号相反
加速度的方向
3
\(\Delta v\)(速度变化量)与\(a\)的方向关系
\(\Delta v\)为正a也为正吗?
是
加速度的方向
3
5.如图,是某质点的v-t图。
(1)该质点在0~4 s内、4~6 s内、6~10 s内、10~14 s内的加速度的大小依次为 1.5 m/s2、1 m/s2、0 m/s2、1 m/s2。
(2)该质点在6~10 s内做匀速直线运动;
(3)该质点在整个运动过程中的最大速度为6m/s。
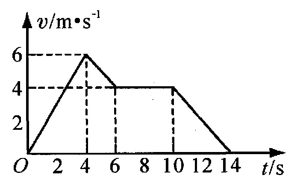
结论:加速时a为正,减速时a为负
加速度的方向
3
加速度也是矢量,加速度的方向即速度变化量的方向。
物体在一直线上运动,速度增大,加速度为正值;速度减小,加速度为负值。
加速时,速度与加速度同向;
减速时,加速度与速度反向。
否,v变大是由a、v同向决定的,与a的变化无关
a变大v也变大吗?
6.关于做直线运动的物体的加速度方向,下列判断正确的是( C )
(A)加速度的方向就是速度的方向
(B)加速度的方向就是位移的方向
(C)当物体做加速运动时,加速度的方向与速度的方向相同
(D)当物体做减速运动时,加速度的方向与速度的方向相同
7.关于物体的下列运动中,不可能发生的是( )
(A)加速度逐渐减小,而速度逐渐增大
(B)加速度方向不变,而速度的方向改变
(C)加速度大小不变,方向改变,而速度保持不变
(D)加速度逐渐增大,而速度逐渐减小
8.物体做变速直线运动,在t=0时速度大小为1 m/s,方向向东;在t=2 s时速度大小为3 m/s,方向向西。则在此过程中该物体的加速度( D )
(A)大小为1 \(\rm m/s^2\),方向向东 (B)大小为1 \(\rm m/s^2\),方向向西
(C)大小为2 \(\rm m/s^2\),方向向东 (D)大小为2 \(\rm m/s^2\),方向向西
2.在直线运动中,加速度的方向用正负号来表示,正号表示加速度与初速度同向,负号表示加速度与初速度反向。
3.在v-t图像中,纵轴截距代表初速度,斜率代表加速度。
\(v\)
\(t\)
\(v_0\)
\(t\)
\(v_t\)
5.如图,是一个物体向东运动的v-t图。
(1)由图可知,在0~10 s内物体的加速度大小为3m/s2,方向向东;
(2)在40~60 s内物体的加速度大小为1.5m/s2,方向向西。
9.如图,为某质点做直线运动的v-t图,下列说法正确的是( B )
(A)质点始终向同一方向运动
(B)在运动过程中,质点运动方向发生变化
(C)0~t1 s内质点的加速度方向与运动方向相反
(D)t2~t3 s内质点的加速度方向与运动方向相同
10.用位移传感器、数据采集器和计算机等器材测量运动物体的加速度,如图,为该实验得到的图像,下列说法不正确的是( A )
(A)使用位移传感器实验操作时比较方便,可直接用s-t图处理数据
(B)位移传感器测得一系列数据,通过数据采集器和计算机可转化为v-t图
(C)不能在计算机软件界面得到加速度随时间变化的图像
(D)能采集到整个运动过程的数据,可以通过图像分析物体速度的变化情况
12.航空母舰上的飞机弹射系统可以缩短战机起跑的位移,假设弹射系统对战机作用了0.1 s时间后,可以使战机达到一定的初速度,然后战机在甲板上起跑,加速度为2 m/s2,经过10 s,达到起飞的速度50 m/s的要求,则战机离开弹射系统瞬间的速度是多少?弹射系统所提供的加速度是多少?
\(t_1=0.1 \rm s\)
\(t_2=10 \rm s\)
\(v_2=50 \rm m/s\)
\(v_2=50 \rm m/s\)
\(v_1=?\rm m/s\)
\(v_0=0\)
\(a_1=? \rm m/s^2\)
\(a_2=2 \rm m/s^2\)
1.篮球以10 m/s的速度水平撞击篮板后以8 m/s的速度反向弹回,球与板的接触时间为0.1 s,则篮球在水平方向的加速度大小为180m/s2,方向为与初速度方向相反(选填“相同”或“相反”)。
\(v\)
0.1
-8
\(t\)
10
2.某物体做直线运动,某时刻速度大小为4 m/s,经过1 s后的速度的大小为10 m/s,那么在这1 s内,物体的加速度的大小可能为6或14m/s2。
3.物体以5 m/s的初速度沿光滑斜槽向上做直线运动,经4 s滑回原处时速度大小仍为5 m/s,则物体的速度变化为-10m/s,加速度为-2.5m/s2。(规定初速度方向为正方向)
\(v\)
4
-5
\(t\)
5
4.如图,为甲、乙两质点做直线运动的v-t图,由图中可以看出,甲比乙运动得快的时间段是\(t_3\)之后,甲的加速度比乙大的时间段是0~\(t_1\),\(t_2\)之后。

5.如图,是汽车在一段平直公路上行驶的v-t图。由图像可知,汽车在前15 s内的加速度大小为1.3m/s2,方向为正(选填“正”或“负”);中间10 s内的加速度为0m/s2;后15 s内的加速度大小为2m/s2,方向为负(选填“正”或“负”)。
8.一个质点做方向不变的直线运动,加速度的方向始终与速度方向相同,但加速度大小逐渐减小直至为零,则在此过程中( )
(A)速度逐渐减小,当加速度减小到零时,速度达到最小值
(B)速度逐渐增大,当加速度减小到零时,速度达到最大值
(C)位移逐渐增大,当加速度减小到零时,位移不再增大
(D)位移逐渐减小,当加速度减小到零时,位移达到最小值
例如:逐渐松油门的汽车启动
第一章F 匀加速直线运动
匀变速直线运动
1

最早系统研究匀加速直线运动的物理学家是伽利略
结论:经过的距离与时间的平方成正比例
匀变速直线运动
1
速度随时间均匀变化的直线运动叫做匀变速直线运动。
匀变速直线运动是加速度大小和方向均不随时间变化的运动。
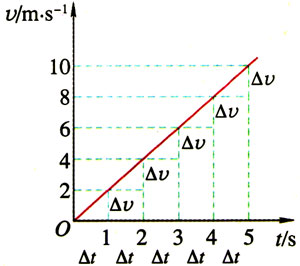
初速为零的匀加速直线运动
2
(1)瞬时速度\(v_t\)与时间\(t\)的关系
由\(a=\frac{v_t-v_0}{t}\)可知
\(v_t=v_0+at\)
注意:\(v_t\)指的是\(t\)末的瞬时速度
初速为零的匀加速直线运动
2
\(v_t=v_0+at\)
一辆小客车从静止出发做加速度\(a=2 \rm m/s^2\)的匀加速直线运动。求此车:
(1)第4s末的速度;
(2)第3s初的速度。
(1)瞬时速度\(v_t\)与时间\(t\)的关系
初速为零的匀加速直线运动
2
(2)位移\(s\)与时间\(t\)的关系
\(v\)
\(t\)
\(v\)-\(t\)图像的“面积”表示位移
\(v\)
\(t\)
\(s=vt\)
\(v\)
\(t\)
\(v_t\)
\(t\)
\(s=\frac{1}{2}v_t t =\frac{1}{2}at \times t =\frac{1}{2}at^2\)
注意:\(s\)指的是\(t\)秒内的位移
一辆小客车从静止出发做加速度\(a=2 \rm m/s^2\)的匀加速直线运动。求此车:
(1)4s内的位移;
(2)第4s内的位移。
初速为零的匀加速直线运动
2
(2)位移\(s\)与时间\(t\)的关系
\(s=v_0t+\frac{1}{2}at^2\)
位移公式:\(s=v_0t\)
\(v\)
\(t\)
\(v_0\)
\(t\)
\(s=v_0t\)
\(v\)
\(t\)
\(v_0\)
\(t\)
\(s=v_0t\)
匀速直线运动
匀变速直线运动
速度公式:\(v_t=v_0\)
速度公式:
位移公式:
\(v_t\)
\(v_t=v_0\)
\(v_0t\)
\(at\)
\(v_0\)
\(\frac{1}{2}at^2\)
\(v_t\)
\(+at\)
\(+\frac{1}{2}at^2\)
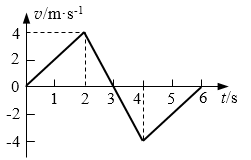
10.某物体沿一直线运动,其v-t图如图,则下列说法正确的是(C )
(A)第2 s内和第3 s内速度方向相反
(C)第3 s内速度方向与加速度方向相反
(B)第2 s内和第3 s内的加速度方向相同
(D)第4 s内速度方向与加速度方向相反
同步学典P30
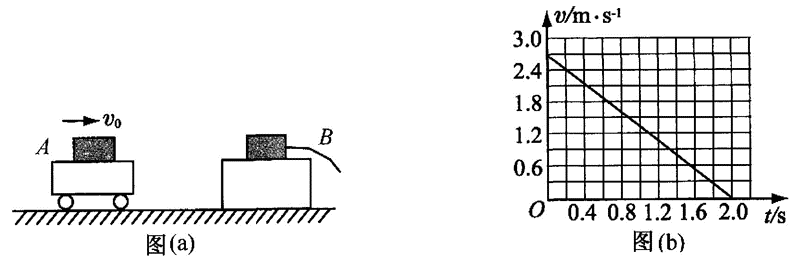
11.如图(a),是用DIS测定小车刹车时加速度的实验装置。
(1)信号发射部分和信号接收部分组成位移传感器,A是信号发射器部分;
(2)这组传感器所直接测量的物理量是位移;
(3)如图(b),是根据实验数据得到的v-t图,根据图像中数据可求出小车的加速度大小为1.35m/s2。
同步学典P30
12.有些国家的交管部门为了保证交通安全,特制定了死亡加速度为500g(g取10 \(\rm m/s^2\))这一数值以警示世人,意思是如果行车加速度达到此值,将有生命危险。这么大的加速度,一般车辆是达不到的;但是,如果发生交通事故时,将会达到这一数值。试判断:两辆摩托车以36 km/h的速度相向而撞,碰撞时间为\(2 \times 10^{-3} \rm s\),驾驶员是否有生命危险?
同步学典P30
有危险
3.摩托车从静止开始以\(a_1=1.6\rm m/s^2\)的加速度沿直线匀加速行驶了\(t_1=4 \rm s\)后,又以\(a_2=1.2\rm m/s^2\)的加速度沿直线匀加速行驶了\(t_2=3 \rm s\),然后做匀速直线运动,则摩托车做匀速直线运动时速度的大小是10m/s。
同步学典P31
\(v \rm/m·s^{-1}\)
\(t \rm/s\)
10
6.4
4
7
9.物体从静止开始做匀加速直线运动,第3 s内通过的位移是3 m,则( D )
(A)前3 s的位移是6 m (B)3 s末的速度是3 m/s
(C)3 s内平均速度是2 m/s (D)物体的加速度是1.2 m/s2
同步学典P32
2.竖直向上发射的火箭,刚开始升空时的加速度约为20 \(\rm m/s^2\),若火箭做匀加速直线运动,加速3 s后火箭的速度为多大?火箭离发射处高度为多大?
教材练习册P31/2
3.登山运动员登山时,发现山坡上距他1000 m处出现雪崩,根据山的坡度可估计出雪块下滑的加速度约为5 \(\rm m/s^2\),他有多少时间逃离现场?
教材练习册P31/3
4.自行车从静止开始做匀加速直线运动,经10 s后速度变为5 m/s,则这段时间内速度的变化是5m/s,加速度是______\(\rm m/s^2\),位移是____m。
教材练习册P31/4
10.一质点从静止开始做匀加速直线运动,质点在第3 s内的位移为15 m,求:
(1)物体在第6 s内的位移为多大?
(2)物体在前6 s内的位移为多大?
(3)质点运动的加速度大小?
(4)质点经过12 m位移时的速度为多少?
(2)物体在前6 s内的位移为多大?
教材练习册P31/10
初速为零的匀加速直线运动
2
(3)瞬时速度与加速度、位移的关系
\(s=\frac{1}{2}at^2\)
\(v_t=at\)
由
解得时间
\(t=\frac{v_t}{a}\)
代入位移公式
\(=\frac{1}{2}a(\frac{v_t}{a})^2\)
\(=\frac{v_t^2}{2a}\)
\(v_t^2-v_0^2=2as\)
初速为零的匀加速直线运动
2
(3)瞬时速度与加速度、位移的关系
\(s=\frac{1}{2}at^2\)
\(v_t=at\)
由
解得时间
\(t=\frac{v_t}{a}\)
代入位移公式
\(=\frac{1}{2}a(\frac{v_t}{a})^2\)
\(=\frac{v_t^2}{2a}\)
\(v_t^2-v_0^2=2as\)
\(v\)
\(t\)
\(v_0\)
\(t\)
\(s=v_0t+\frac{1}{2}at^2\)
匀变速直线运动
位移公式:
\(v_t\)
\(v_0t\)
\(at\)
\(v_0\)
\(\frac{1}{2}at^2\)
\(v\)
\(t\)
\(v_0\)
\(t\)
\(s=\frac{v_0+v_t}{2}t=\bar{v}t\)
\(v_t\)
梯形面积还可以如何表达?
推论:在匀变速直线运动中
\(\bar{v}=\frac{v_0+v_t}{2}\)
同步P34/1
1.从长3 m的斜面顶端由静止滚下来的小球,末速度是2.5 m/s,则小球滚动所用的时间为2.4s。
先用
审题:已知\(s\)、\(v_0\)、\(v_t\),求\(t\)
求
再用
求
同步P40/1
物体做初速度为\(v_0\)的匀变速直线运动,经过时间t,物体的速度达到\(v_t\),则在这段时间内的平均速度\(\bar{v}\)=_________。如果物体在第1 s末速度为\(v_1\),第4 s末的速度为\(v_2\),则这3 s内的平均速度\(\bar{v}\)=_________,这3 s内的位移可表示为s=___________。
同步P34/2
2.某飞机的起飞速度是60 m/s,在跑道上可能产生的最大加速度为4 m/s2,该飞机从静止到起飞成功需要跑道的最小长度为450m。
审题:已知\(v_0\)、\(v_t\),\(a\)、求\(s\)
用
同步P34/3
3.由静止开始做匀加速直线运动的物体,当经过s位移时的速度是v,那么位移为4s时的速度是2v。
审题:已知\(v_0\)、\(v_t\),\(s\),且\(a\)不变
先用
求
再用
求
同步P34/6
6.A、B两物体均做匀变速直线运动,A的加速度a1=1.0 m/s2,B的加速度a2=-2.0 m/s2,根据这些条件作出的下列判断,其中正确的是( A)
(A)A的加速度小于B的加速度
(B)A做的是匀加速运动,B做的是匀减速运动
(C)两个物体的运动方向一定相反
(D)任意时刻两个物体的速度都不可能为零
同步P35/8
8.物体从静止开始做匀加速直线运动,已知第3 s内与第2 s内的位移之差是6 m,则可知( )
(A)第1 s内的位移为4 m
(B)第2 s末的速度为12 m/s
(C)物体运动的加速度为3 m/s2
(D)物体在前4 s内的平均速度为15 m/s
同步P35/11
11.物体A从静止出发,以2 m/s2的加速度向前运动。第3 s末在同一地点物体B也从静止出发以3 m/s2的加速度沿A运动方向前进。求:
(1)第5 s末物体A的速度大小;
(2)5 s内物体A的平均速度大小;
(3)第5 s内物体A的位移大小;
(4)第5 s末AB两物体相距多远?
(1)10m/s
(2)5m/s
(3)9m
(4)19m
同步P36/1
1.由静止开始做匀加速直线运动的物体前2 s内的平均速度为2 m/s,则前2 s内物体的位移为4m,此物体的加速度等于2m/s2,前5 s内的平均速度等于5m/s。
(1)
(2)
(3)
和
同步P36/2
2.某物体从静止开始做匀加速直线运动,第1 s内通过的位移为2 m,则第1 s末的速度为4m/s,前2 s内的位移为8m,前3 s内的平均速度为6m/s,第4 s内的位移为14m。
先用
求
再用
求
同步P36/3
3.物体由静止开始做匀加速直线运动,位移为s时,速度为v,当速度增大到原来的3倍时,该物体离开出发点的距离是9s。
审题:已知\(v_0\)、\(v_t\),\(s\),且\(a\)不变
同步P37/10
10.物体由静止开始做匀加速直线运动,加速度大小是2 m/s2,它在某1 s内通过的距离是15 m。求:
(1)物体在这1 s初的速度是多少?14 m/s
(2)物体在这1 s以前已运动了多长时间?7s
(3)物体在这1 s以前已经通过了多少路程?49m
(1)
(2)
(3)
审题:已知\(a\)、\(t\),\(s\),求\(v_0\)
第一章 G 自由落体运动
Title Text

同步P33/1
1.一个由静止开始做匀加速运动的物体,它的加速度是0.2 m/s2,则此物体在4 s末时的速度为0.8m/s,4 s初时的速度为0.6m/s,它在第5 s内的中间时刻的速度为0.9m/s 。
同步P33/2
2.某质点做初速度为零的匀加速直线运动,若将全程时间分为1∶3两段,则在这两段时间内通过的位移之比为1∶15,平均速度之比为1∶5。
同步P33/3
3.初速度为零的匀加速直线运动在2 s内,4 s内,…,2n s内的位移之比为1∶4∶9∶…∶\(n^2\),在2 s末,4 s末,…,2n s末的瞬时速度之比为 1∶2∶3∶…∶n。
(1)用\(s=\frac{1}{2}at^2\),\(s\)与\(t^2\)成正比
(2)用\(v_t=at\),\(v_t\)与\(t\)成正比
同步P33/4
4.一物体做初速度为零的匀加速直线运动,则它通过前1 m、前2 m、前3 m所需的时间之比为1∶\(\sqrt {2}\)∶\(\sqrt {3}\),平均速度之比为1∶\(\sqrt {2}\)∶\(\sqrt {3}\)。
(1)用\(s=\frac{1}{2}at^2\),
然后:\(t=\sqrt{\frac{2s}{a}}\)
\(t\)与\(\sqrt{s}\)成正比
(2)用\(\bar{v}=\frac{s}{t}\)
同步P33/6
6.质点从静止开始做匀加速直线运动,从开始运动起,通过连续三段路程所用的时间分别为1 s、2 s、3 s,则这三段路程之比应为 ( D )
(A)1∶2∶3 (B)1∶3∶5 (C)1∶4∶9 (D)1∶8∶27
同步P33/7
7.从静止开始做匀加速直线运动的物体,下列说法中,正确的是 ( D )
(A)1 s,2 s,3 s内的平均速度之比是1∶2∶3
(B)1 s,2 s,3 s内的中间时刻瞬时速度之比是1∶2∶3
(C)第1 s内,第2 s内,第3 s内的平均速度之比是1∶2∶3
(D)第1 s末,第2 s末,第3 s末的瞬时速度之比是1∶2∶3
(D)用\(v_t=at\),\(v_t\)与\(t\)成正比
同步P33/9
9.物体从斜面顶端由静止开始下滑,经时间t到达中点,则物体从斜面顶端到底端共用时间为 ( A )
(A)\(\sqrt{2}t\) (B)\(\sqrt{t}\) (C)\(2t\) (D)\(\frac{\sqrt{2}}{2}t\)
\(t\)
同步P33/10
10.钢球在斜槽上做初速度为零的匀加速直线运动,开始运动后0.1 s内通过的路程为3 cm。求 :
(1)第1 s内通过的路程;
(2)若斜面长1.5 m,钢球由斜面顶端滚到底端需要的时间是多少?
(1)
(2)
同步P34/4
4.某物体由静止开始做匀加速直线运动,在4 s内的位移是64 m,则物体经过前一半位移所需的时间是\(2\sqrt{2}\)s,物体在前一半时间内所通过的位移是16m 。
(1)
4s,64m
t=?,32m
(2)
4s,64m
t=2s,s=?
同步P34/5
5.一辆汽车由静止开始做匀加速直线运动,共经过12 m位移。若把这段位移分成两段,使通过每段位移的时间相等,则第一段位移的大小为3m,若使它运动时间再增加原来的一倍,则汽车的位移将增加36m 。
同步P34/7
7.质点做初速度为零的匀加速直线运动,它在第一个2 s、第二个2 s和第5 s三段时间内的位移之比是 ( C )
(A)2∶6∶5 (B)2∶8∶7 (C)4∶12∶9 (D)2∶2∶1
同步P35/10
10.一列火车从静止开始做匀加速直线运动,一个人站在第一节车厢前观察,第一节车厢通过他历时2 s,全部列车通过他历时6 s,求列车共有几节车厢 ?
解:设一节车厢长度为s
P2/1
1.已知某沿直线运动的质点的运动规律为s=4t(2-t)(t以s为单位,s以m为单位),则它的初速度大小为8m/s,加速度大小为8m/s2。
P2/2
2.一辆汽车刹车后做匀减速直线运动,其初速度为10 m/s,加速度大小为2 m/s2,则其通过前21 m所需的时间为3s。
P2/3
3.以大小为20 m/s的速度在一条直线公路上匀速行驶的汽车,刹车后经过5 s停止运动,则刹车后汽车的加速度大小为4m/s2,汽车在刹车过程中所经过的位移为50m。
同步P2/4
4.一列火车制动后开始做匀减速直线运动,经20 s停止,在这段时间内火车的位移是120 m,则火车开始制动时的速度为12m/s,制动后到停下过程中它的加速度为-0.6m/s2。
(1)用\(s=\frac{v_0+v_t}{2}t\)
(2)用\(a=\frac{v_t-v_0}{t}\)
或\(a=\frac{v_t^2-v_0^2}{2s}\)
同步P2/5
5.汽车以36 km/h的速度行驶,刹车后加速度的大小为4 m/s2,从刹车开始,经过1 s时间汽车通过的距离为8m,经过3 s时间汽车通过的距离为12.5m。
【2.5s已停】
同步P3/7
7.汽车做匀速直线运动的速度为10 m/s,某时刻突然刹车,刹车后汽车的加速度大小为5 m/s2,则刹车后3 s内的位移为10m,刹车后第2 s内的位移为2.5m。
【2s已停】
同步P3/8
8.汽车以20 m/s的速度做匀速直线运动,刹车后以大小为5 m/s2的加速度做匀减速直线运动,那么刹车后2 s内与刹车后6 s内汽车通过的位移之比为3∶4。
【4s已停】
2秒
2秒
s
3s
【逆向比例法】
同步P3/9
9.从地面竖直向上抛出一个物体,物体匀减速上升,经2 s到达离地44 m高处,此时物体的速度大小为10 m/s,方向向上,则其运动的加速度为-12m/s2,抛出时的初速度为34m/s。
同步P3/10
10.一架飞机刚开始着陆减速时的速度为50 m/s,加速度大小为5 m/s2,那么在着陆后的12 s内飞机的位移应该是( C )。
(A)600 m (B)360 m (C)250 m (D)240m
【10s已停】
同步P3/11
11.汽车刹车后做匀减速直线运动,经时间4 s停止,在刹车之后的1 s内、2 s内、3 s内汽车通过的路程之比为( C )。
(A)3∶5∶7 (B)5∶8∶9 (C)7∶12∶15 (D)1∶4∶9
1秒
s
3s
1秒
1秒
1秒
7s
5s
同步P3/12
12.一物体做匀减速直线运动,初速度为12 m/s,加速度大小为2 m/s2,该物体在某1 s内的位移为6 m,此后它运动6.25m速度为零。
t=1秒,s=6米
\(v_0=?\)
\(a=2\rm m/s^2\)
s=?
同步P4/14
14.一物体做匀减速直线运动,加速度的大小为2 m/s2,运动2 s后,末速度为其初速度的一半,求:
(1)物体在此2 s内的位移;12m
(2)物体从减速开始到停下所通过的距离。16m
(1)\(v_t=v_0+at\)
\(\frac{v_0}{2}=v_0+at\)
\(v_0=8 \rm m/s\)
\(s=\frac{v_0+v_t}{2}t=12 \rm m\)
审题:已知\(a,t,v_t=\frac{v_0}{2}\)
(2)\(s=\frac{v_0+v_t}{2}t\) 或 \(s=\frac{v_t^2-v_0^2}{2a}\)
同步P4/15
15.如图,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18 m。该车加速时最大加速度大小为2 m/s2,减速时最大加速度大小为5 m/s2,此路段允许行驶的最大速度为12.5 m/s。
(1)如果立即做匀加速运动,试通过计算说明汽车是否能在绿灯熄灭前通过停车线;
(2)如果立即做匀减速运动,试通过计算说明汽车是否安全。
第一章 直线运动
By fjphysics
第一章 直线运动
高一第一学期
- 517



