第三章A 牛顿第一定律 惯性
1
伽利略的斜面理想实验
要使一个物体运动起来必须有力的推它、拉它。当力停止作用后，运动物体便静止不动。
要使一个物体运动得更快，要用更大的力推它。
要保持一个物体做匀速运动，必须有一个恒定的力作用于它。
论断：力是维持物体运动的原因。
1
伽利略的斜面理想实验
论断：力是维持物体运动的原因。
论断：维持物体运动不需要力。
1
伽利略的斜面理想实验
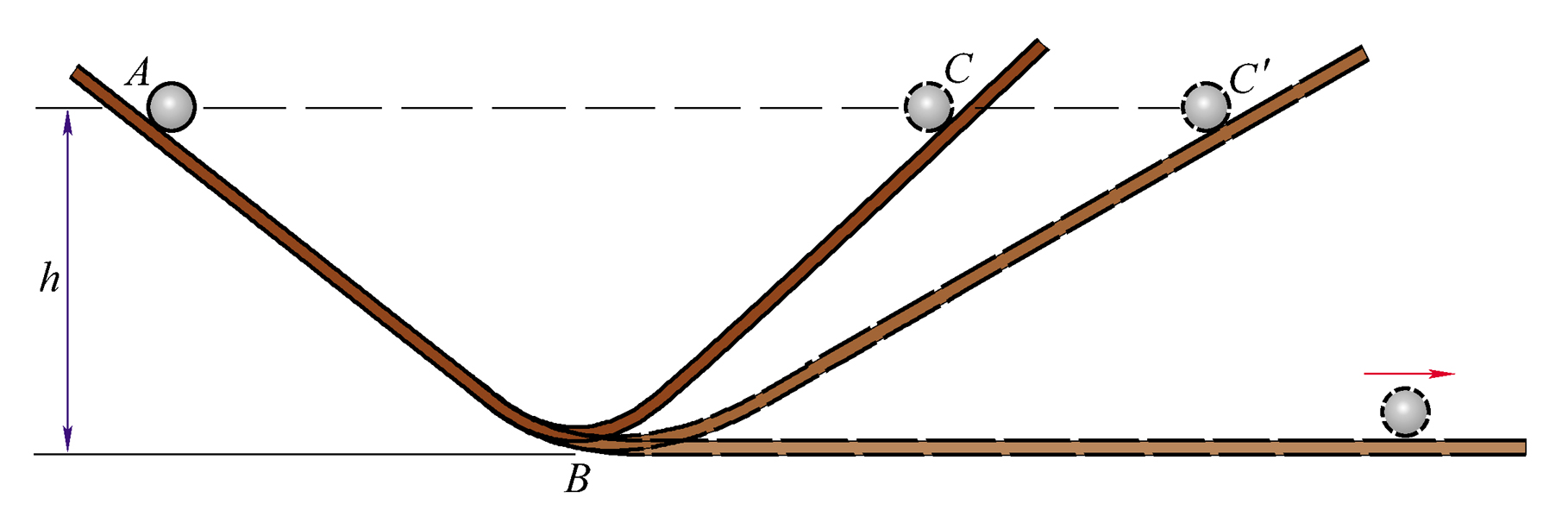
将小球从斜面的某一高度处由静止释放，小球将滚上另一个斜面。
如果没有摩擦，小球将上升到原来高度
如果减小斜面倾角，小球将通过更长的路程，最终仍能到达原来的高度
当BC最终成为水平面时，小球再也达不到原来的高度，而沿水平面以恒定的速度一直运动下去。
1
2
3
4
2
牛顿第一定律
一切物体总保持匀速直线运动状态或静止状态，直到有外力迫使它改变这种状态为止。
3
惯性
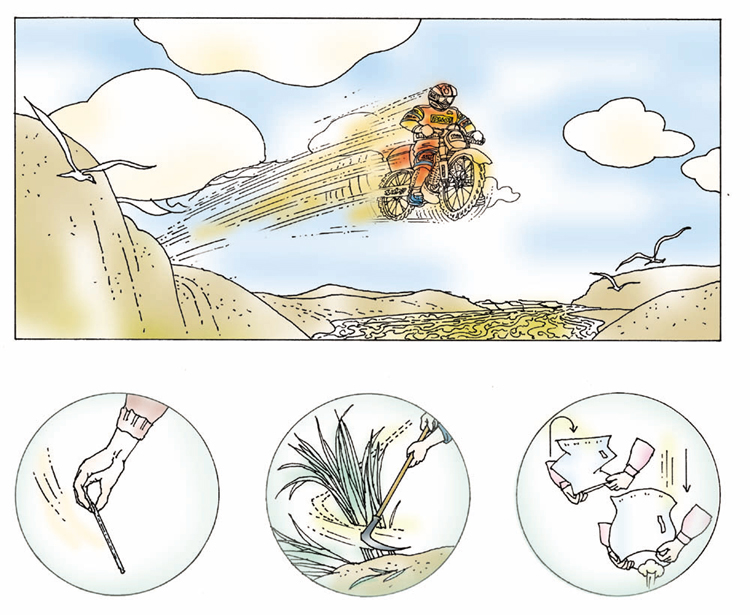
用“物体具有惯性”说明以下现象
物体保持原来匀速直线运动状态或静止状态的性质叫做惯性。
切勿说成“在惯性的作用下”
质量是物体惯性大小的量度。
4
牛顿的最主要的贡献
万有引力定律
反射望远镜
光的色散
《自然哲学的数学原理》
微积分
第三章B 牛顿第二定律
1
力是改变物体运动状态的原因
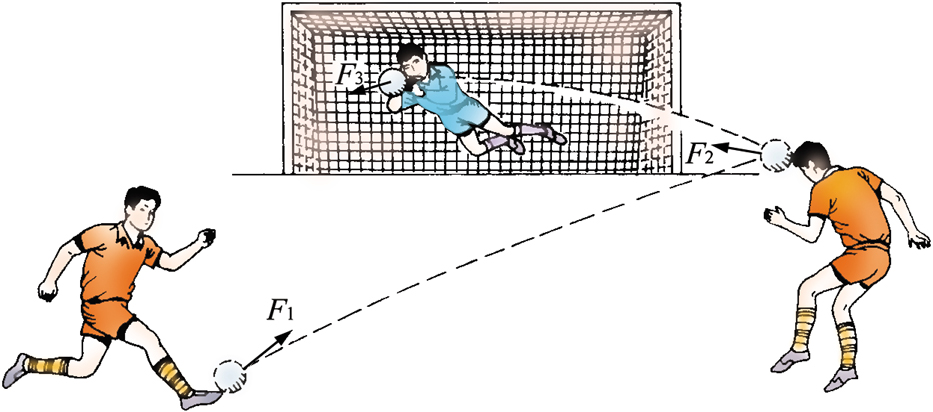
速度增加
速度减少
速度方向改变
\(v\)改变，即\(\Delta v≠0\)，即\(a=\frac{\Delta v}{\Delta t}≠0\)
力是产生加速度的原因
2
加速度与作用力的关系
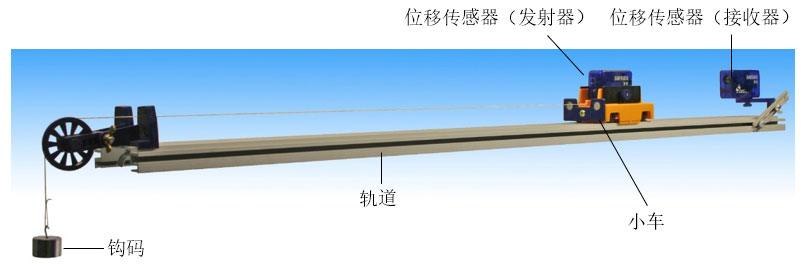
控制小车质量\(m\)不变
\(a\)
\(F\)
以钩码重力作为小车所受外力\(F\)
\(G\)
\(F\)
\(m\)
\(a\)
用DIS位移传感器测量小车加速度\(a\)
结论：在质量一定的情况下，加速度\(a\)与作用力\(F\)成正比，即：\(a \propto F\)
同步P110/10（2009年上海高考）
图（a）为“用DIS研究加速度与力的关系”的实验装置。
（1）在该实验中必须采用控制变量法，应保持________不变，用钩码所受的重力作为___________，用DIS测小车的加速度；
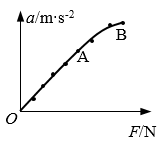
（2）改变所挂钩码的数量，多次重复测量。在某次实验中根据测得的多组数据可画出a-F关系图线如图（b）。
①分析此图线的OA段可得出的实验结论是____________。
②（单选）此图线的AB段明显偏离直线，造成此误差的主要原因是（ ）
（A）小车与轨道之问存在摩擦 （B）导轨保持了水平状态
（C）所挂钩码的总质量太大 （D）所用小车的质量太大
2
加速度与质量的关系
通过增减配重片改变小车质量\(m\)
\(a\)
\(m\)
钩码重力作为小车所受外力\(F\)不变
\(G\)
\(F\)
\(m\)
\(a\)
用DIS位移传感器测量小车加速度\(a\)
结论：在相同的力作用下，物体的加速度跟物体的质量成反比，即：\(a \propto \frac{1}{m}\)
同步P134/17
利用计算机辅助实验系统可定量研究加速度a与作用力F及小车质量m的关系。
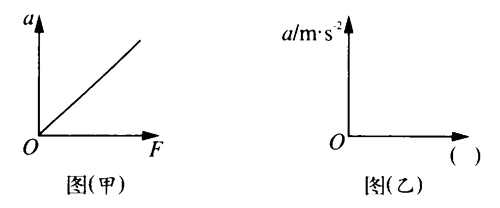
（1）当小车质量m一定时，测得小车在不同力F作用下运动的加速度a；得到如图（甲）的a-F图线后，并由此得出结论：质量一定，加速度与外力成正比。
（2）当作用力F一定时，测得小车加速度a与小车质量m的关系，如表（略）：
为了清晰明确的研究a与m的准确的定量关系，在如图（乙）图像的横轴括号中，应填上对应的物理量的符号为___，并得出结论：_________________________________。
2
加速度与作用力的关系，加速度与质量的关系
将两个实验结论总括起来，即
a \propto \frac{F}{m}
或
F \propto ma
F =kma
如果规定质量为\(1 \rm kg\) 的物体产生\(1 \rm m/s^2\)加速度时所需的力为\(1 \rm N\)，则\(k=1\)。
F =ma
3
牛顿第二定律
物体的加速度\(a\)与受到的作用力\(F\)成正比，与物体的质量\(m\)成反比。
物体受几个力作用时，牛顿第二定律公式中的\(F\)即为合力。
F=ma
F_合=ma
\(F_合\)与\(a\)的大小与方向是瞬时对应关系。
\(v\)的方向与\(a\)的方向（即\(F\)的方向）之间没有必然关系。
3
牛顿第二定律
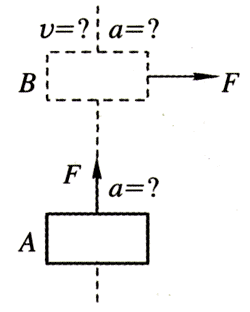
如图所示是一光滑平面的俯视图，
（1）物体在该平面的A位置时受到向前的作用力，其加速度向什么方向？
（2）在B位置，作用力改成水平向右，此时物体的加速度方向如何？
（3）若突然撤去外力，其加速度方向又如何？
\(v\)的方向与\(a\)的方向（即\(F\)的方向）之间没有必然关系。
\(F_合\)与\(a\)的大小与方向是瞬时对应关系。
\(F\)
\(F\)
4
质量是物体惯性大小的量度
根据牛顿第二定律\(a＝\frac{F}{m}\)，在外力\(F\)一定的情况下，
物体的质量\(m\)越大，加速度\(a\)越小，运动状态越难改变；
物体的质量\(m\)越小，加速度\(a\)越大，运动状态越容易改变。
所以物体惯性的大小取决于物体的质量，而与物体的速度无关。
目前为止，咱们会做这么几道题目
\(F\)
\(N\)
\(G\)
F=ma
F-f=ma
\(G\)
\(N\)
\(F\)
\(a\)
\(a\)
\(f\)
\(a\)
T-G=ma
\(G\)
\(T\)
\(N\)
\(G\)
G-N=ma
\(a\)
光滑水平面
粗糙水平面
超重
失重
第三章C 作用与反作用牛顿第三定律
1
作用力和反作用力
力是物体对物体的作用。
有受力物体，就必有施力物体，力不能脱离物体而独立存在。
\(F\)
\(F'\)
1
作用力和反作用力
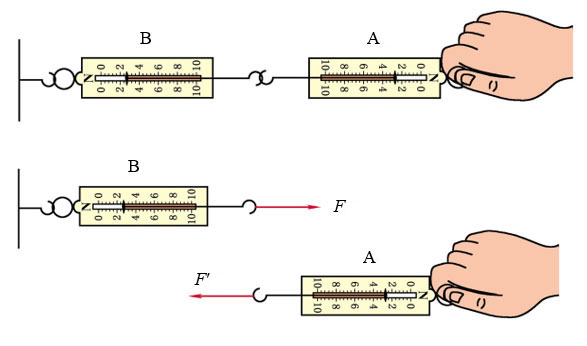
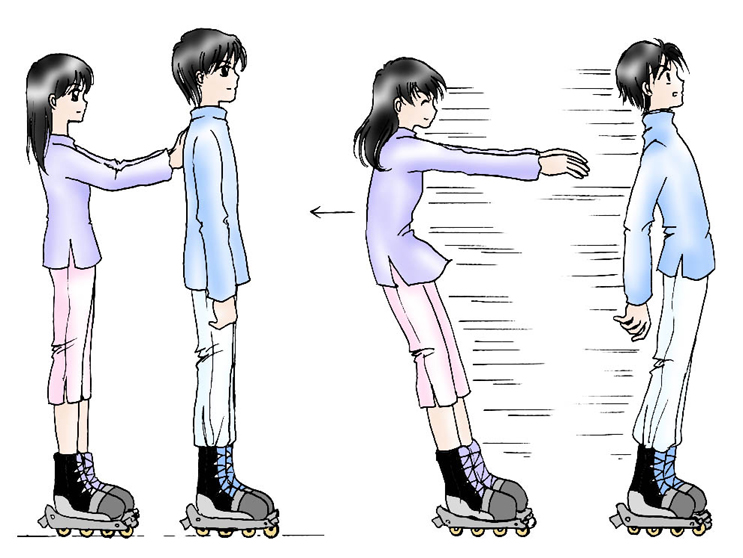
在任何情况下物体间力的作用总是成对出现的。我们可以把其中任意一个叫做作用力，那么另一个就是反作用力。
A对B的拉力
B对A的拉力
1
作用力和反作用力
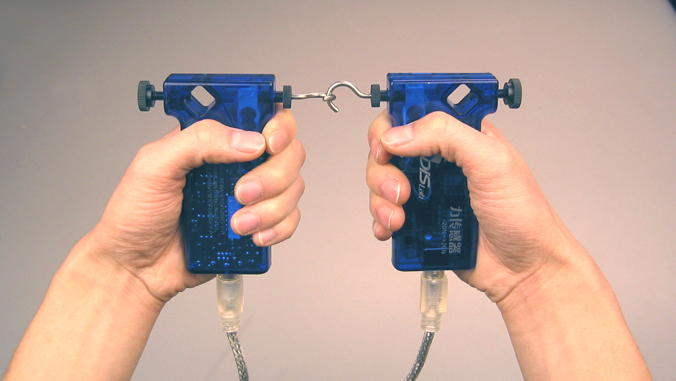
作用力和反作用力大小相等，方向相反，作用在同一条直线上，且同时产生，同时消失。
2
牛顿第三定律
两个物体之间的作用力和反作用力大小相等，方向相反，作用在同一条直线上，即
F=F'
2
牛顿第三定律
（1）
作用力和反作用力分别作用在两个不同的物体上。
\(F\)
\(F'\)
铁钉对锤子的力，作用在锤子上
锤子对铁钉的力，作用在钉子上
2
牛顿第三定律
（2）
作用力和反作用力是同种性质的力。
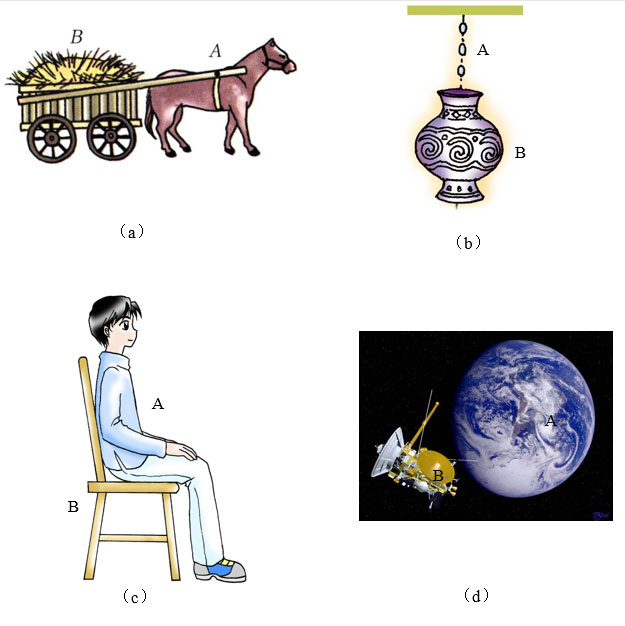
\(T\)
\(T'\)
铁链对花瓶的拉力
花瓶对铁链的拉力
两者都是弹力
\(G\)
\(G'\)
地球对卫星的引力
卫星对地球的引力
两者都是重力（万有引力）
2
牛顿第三定律
\(T\)
\(T'\)
\(T\)
\(G\)
作用力与反作用力
平衡力
大小相等，方向相反，作用在同一条直线上
作用在两个不同的物体上
同种性质
同时产生、同时消失
2
牛顿第三定律
一物体静止在水平面上，
试证明物体对地面的压力大小等于物体所受的重力大小。
\(G\)
\(N\)
2
牛顿第三定律
第三章D 牛顿运动定律的应用
1
物理量的单位和力学单位制
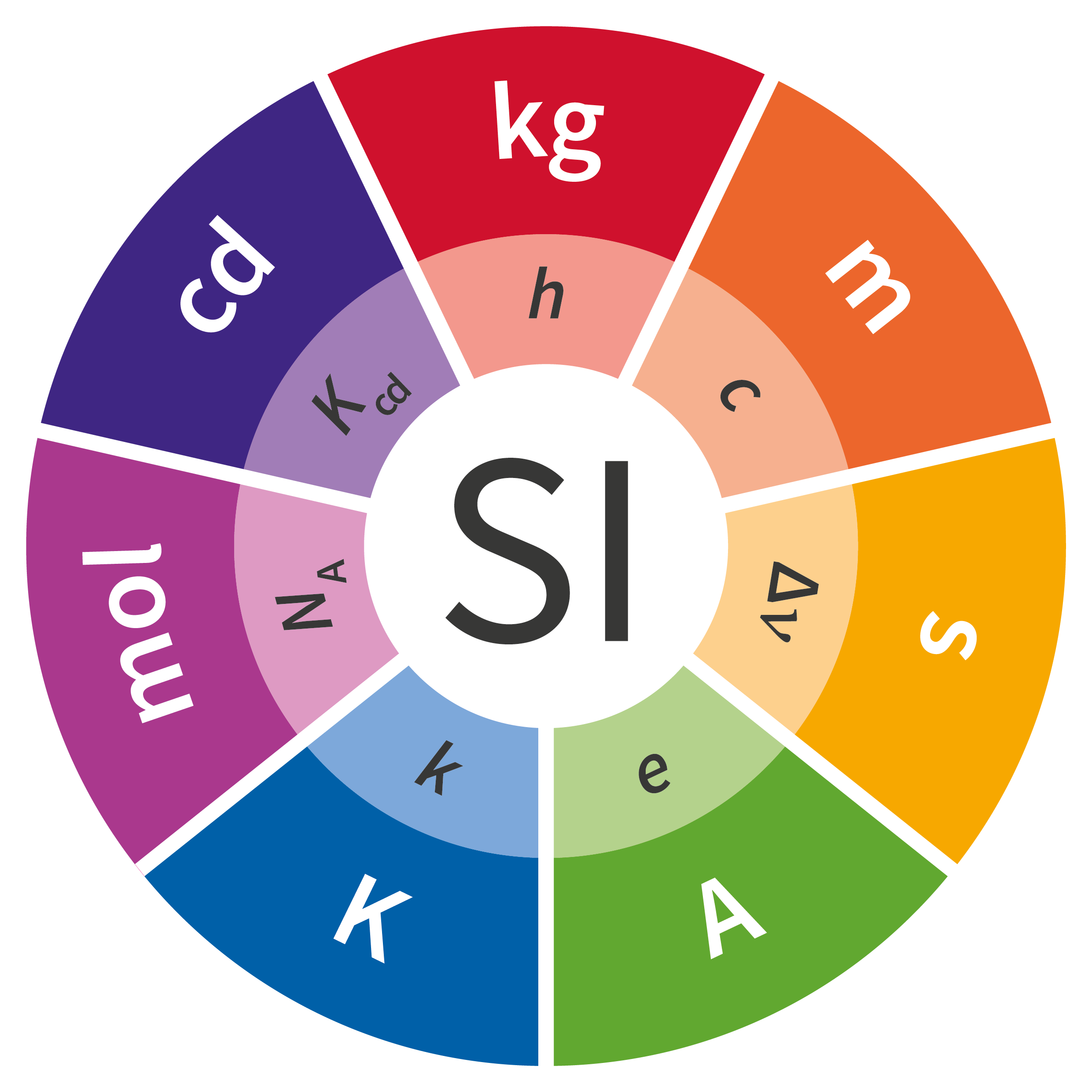
国际单位制的基本单位
国际单位制的导出单位
1
7
6
5
4
3
2
米（m）
开（K）
长度
质量
电流
发光强度
摩尔（mol）
千克（kg）
时间
秒（s）
安培（A）
温度
物质的量
坎德拉（cd）
速度
加速度
力
压强
功
电压
……
\(\rm m/s\)
\(\rm Pa\)
\(\rm N\)
\(\rm m/s^2\)
\(\rm V\)
\(\rm J\)
……
之前，咱们会做这么几道题目
\(F\)
\(N\)
\(G\)
F=ma
F-f=ma
\(G\)
\(N\)
\(F\)
\(a\)
\(a\)
\(f\)
\(a\)
T-G=ma
\(G\)
\(T\)
\(N\)
\(G\)
G-N=ma
\(a\)
光滑水平面
粗糙水平面
超重
失重
然后，咱们又会做这么几道题目
\(a=gsin\theta\)
物体在光滑斜面上（下）滑
\(\theta\)
物体在粗糙斜面下滑
\(G\)
\(N\)
\(N\)
\(G\)
\(\theta\)
\(a\)
\(f\)
\(a=gtan\theta\)
物体在变速车厢中
粗糙水平面斜推物体
\(a\)
\(G\)
\(N\)
\(F\)
\(f\)
\(\theta\)
\(\theta\)
\begin{cases}
N=Gcos\theta \\
Gsin\theta-f=ma
\end{cases}
\begin{cases}
N=G+Fsin\theta \\
Fcos\theta-f=ma
\end{cases}
2
牛顿定律的应用
质量为60kg的滑雪运动员，从倾角为30°的斜坡上自静止起滑行。
（1）若不计任何阻力，求滑行的加速度为多大？
（2）若所受阻力是他自身重力的0.1倍，求滑行的加速度为多大？
追问2：若不计任何阻力，运动员靠惯性沿斜坡上滑，加速度为多大？
追问1：质量为70kg的运动员的滑行加速度如何变化？
\(a\)
2
牛顿定律的应用
同步P120/11
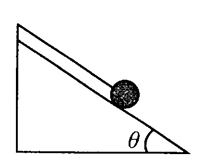
如图，质量为m的小球通过轻绳悬挂在一倾角为θ的光滑斜面上，轻绳与斜面平行，开始时系统处于静止状态。
（1）求系统静止时，绳对小球的拉力大小和斜面对球的支持力大小；
（2）当系统以多大的加速度向左运动，斜面对小球支持力恰好为零？
\(T\)
\(N\)
\(G\)
\(\theta\)
\(T=mgsin\theta\)
\(N=mgcos\theta\)
三力平衡，用合成法，通常不用正交分解法
2
牛顿定律的应用
运动情况
受力情况
两类基本问题
F_合=ma
v_t=v_0+at \newline
s=v_0t+\frac{1}{2}at^2\newline
v_t^2-v_0^2=2as\newline
s=\frac{v_0+v_t}{2}t=\bar vt
\(a\)
“桥梁”
同步P128/10
弹簧测力计的秤钩上挂一个质量为1 kg的物体，在下列情况下，弹簧测力计的读数各为多大？
（1）以0.2 \(\rm m/s^2 \)的加速度沿竖直方向匀加速上升；
（2）以0.2 \(\rm m/s^2 \)的加速度沿竖直方向匀减速下降；
（3）以0.1 \(\rm m/s^2 \)的加速度沿竖直方向匀减速上升；
（4）以0.1 \(\rm m/s^2 \)的加速度沿竖直方向匀加速下降。
同步P128/10
加速上升
减速下降
减速上升
加速下降
\(G\)
\(G\)
\(G\)
\(G\)
\(v\)
\(v\)
\(v\)
\(v\)
3
超重与失重
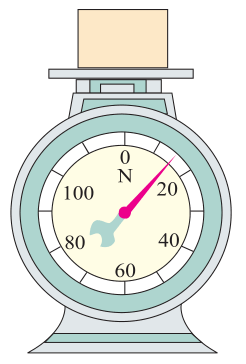
物体对支持物的压力或对悬挂物的拉力大于自身重力的现象叫做“超重”
物体对支持物的压力或对悬挂物的拉力小于自身重力的现象叫做“失重”
\(G\)
\(N\)
\(T\)
\(G\)
\(a\)
\(a\)
超重、失重时物体重力并没有变
\(a\)向上，超重
\(a\)向下，失重
与\(v\)方向无关
第三章E 从牛顿到爱因斯坦
4．牛顿力学只能适用于______、_______领域中的力学现象。
同步P131
6．在相对论中，与静止时相比，运动的钟变________、运动的尺缩________、运动物体的质量变________。时间、空间和质量（即惯性）这三个基本的物理量，在牛顿力学中都是“_____________”，但是在相对论中则都是“________”。
同步P108/3
3．从牛顿第二定律F=ma可知，无论怎样小的力都可以使物体产生加速度，可是当我们用一个很小的力去推地面上一个很重的物体时，却推不动它，这是因为物体所受的合外力为零。
同步P108/5
5．物体在恒力作用下做直线运动，当力与速度方向相同时，物体的加速度和速度方向相同（选填“相同”或“相反”）。物体做匀加速运动；当力与速度方向相反时，物体的加速度与速度方向相反（选填“相同”或“相反”），物体做匀减速运动。
\(v\)的方向与\(a\)的方向（即\(F\)的方向）之间没有必然关系。
\(F_合\)与\(a\)的大小与方向是瞬时对应关系。
同步P108/7
7．下列对牛顿第二定律的讨论中，正确的说法是（D）
（A）根据\(F=ma\)可知，物体所受外力与加速度成正比
（B）根据\(m=\frac{F}{a}\)可知，物体的质量与加速度成反比
（C）根据\(m=\frac{F}{a}\)可知，物体质量与合外力成正比
（D）根据\(a=\frac{F}{m}\)可知，加速度大小与合外力成正比，与质量成反比
因果关系反了
m为物体本身固有属性
同步P108/8
8．关于运动和力的关系，对于质量一定的物体，下列说法正确的是（B）
（A）物体运动的速度越大，它所受的合外力一定越大
（B）物体所受的合外力越大，它的速度变化一定越快
（C）物体所受的合外力越大，它的速度变化一定越大
（D）物体某时刻的速度为零，它此时所受的合外力一定为零
\(a\)是描述速度变化快慢的物理量，即\(a=\frac{\Delta v}{\Delta t}\)
同步P108/9
9．物体运动的速度方向、加速度方向与作用在物体上合外力的方向之间的关系是（B）
（A）速度方向、加速度方向、合外力方向三者总是相同的
（B）速度方向可与加速度成任何夹角，但加速度方向总是与合外力的方向相同
（C）速度方向总是与合外力方向相同，而加速度方向可能与速度方向相同，也可能不相同
（D）速度方向总是与加速度方向相同，而速度方向可能与合外力方向相同，也可能不相同
\(F_合\)与\(a\)的大小与方向是瞬时对应关系。
\(v\)的方向与\(a\)的方向（即\(F\)的方向）之间没有必然关系。
同步P109/4
4．物体在力的作用下做加速直线运动，当力逐渐减小时，物体的加速度将减小，速度将增大；当力减小到零时，物体的加速度为零，速度不变。（均选填“增大”“减小”“不变”或“为零”）
\(F_合\)与\(a\)的大小与方向是瞬时对应关系。
\(v\)的方向与\(a\)的方向（即\(F\)的方向）之间没有必然关系。
同步P109/6
由牛顿第二定律可知（ C ）
（A）由物体运动的方向发生改变，可断定物体所受合外力的方向也改变
（B）只要物体受到力的作用，物体就有加速度
（C）1 N的力可以使质量为1 kg的物体产生1 m/s2的加速度
（D）物体的质量对加速度的产生起反抗作用，所以质量是一种阻力
\(F_合\)与\(a\)的大小与方向是瞬时对应关系。
\(v\)的方向与\(a\)的方向（即\(F\)的方向）之间没有必然关系。
\(v\)
\(v\)
\(G\)
同步P109/7
7．在牛顿第二定律公式F=kma中，比例系数是的数值（ B ）
（A）在任何情况下都等于1
（B）由质量、加速度和力的单位所决定的
（C）由质量、加速度和力的大小所决定的
（D）与质量、加速度和力三者均无关系
如果规定质量为\(1 \rm kg\) 的物体产生\(1 \rm m/s^2\)加速度时所需的力为\(1 \rm N\)，则\(k=1\)。
同步P109/8
8．一个物体受几个力的作用而处于静止状态，若保持其余几个力不变，而将其中一个力F1逐渐减小到零，然后又逐渐增大到F1（方向不变），在这个过程中，物体的（ D ）
（A）加速度始终增大，速度始终增大
（B）加速度始终减小，速度始终增大
（C）加速度和速度都是先增大后减小
（D）加速度先增大，后减小，速度始终增大直到一定值
\(F_合\)与\(a\)的大小与方向是瞬时对应关系。
\(v\)的方向与\(a\)的方向（即\(F\)的方向）之间没有必然关系。
同步P127/3
一个质量为70 kg的人在电梯中用体重计称重，当电梯静止时，体重计读数为700 N；当电梯以a＝g向下做匀加速运动时，读数为0N；当电梯以a＝g向下做匀减速运动时，体重计读数为1400N。（g取10 m/s2）
\(G\)
\(a=g\)
\(N\)
\(N\)
\(a\)
\(G\)
同步P128/8
升降机内的台秤上站立着一个重490 N的人，在升降机沿竖直方向运动时，下列说法正确的是（ D ）
（A）台秤读数为490 N，升降机一定处于匀速上升状态
（B）台秤读数为400 N，升降机一定处于匀加速下降状态
（C）台秤读数为400 N，升降机一定处于匀减速上升状态
（D）以上说法均不对
同步P129/5
某宇宙飞船中的宇航员的质量是60 kg，受到的重力是600 N。起飞阶段向上的加速度是30 m/s2，宇航员对坐椅向下的压力为2400N；重返大气层阶段飞船以5 m/s2的加速度向下做减速运动，字航员对坐椅向下的压力为900N。（g取10 m/s2）
\(G\)
\(a_1\)
\(N\)
\(N\)
\(a_2\)
\(G\)
同步P129/6
下列几种情况中，升降机绳索拉力最大的是（ D ）
（A）以很大速度匀速上升
（B）以很小速度匀速下降
（C）上升时以很大的加速度减速
（D）下降时以很大的加速度减速
同步P130/10
为了测量某住宅大楼每层的平均高度（层高）及电梯运行情况，甲、乙两位同学在一楼电梯内用电子体重计及秒表进行了以下实验：一质量m＝50 kg的甲同学站在体重计上，乙同学记录电梯从地面一楼到顶层全过程中，体重计示数随时间变化的情况，并作出了如图的图像，已知t＝0时，电梯静止不动，从电梯内楼层按钮上获知该大楼共19层（g取10 m/s2）。求：
（1）电梯启动和制动时的加速度大小；
（2）该大楼的层高。3m
\(v\)
\(t\)
2019学年第一学期期末考试
下列所研究的物体，可看作质点的是（ B ）
（A）天文工作者研究地球的自转
（B）用GPS确定远洋海轮在大海中的位置
（C）教练员对游泳运动员的泳姿动作进行指导
（D）乒乓球运动员研究发出的乒乓球的旋转
1
5班：100%；6班：92%
下面哪一组单位属于国际单位制中的基本单位（ C ）
（A）米、牛顿、千克 （B）千克、牛顿、秒
（C）米、千克、秒 （D）秒、千克、焦耳
2
5班：96%；6班：100%
下列关于摩擦力的说法中正确的是（ C ）
（A）物体在运动时才受到摩擦力
（B）摩擦力的方向一定与物体的运动方向相反
（C）摩擦力总是成对地出现
（D）摩擦力的大小总是与正压力的大小成正比
3
5班：24%；6班：16%
下列说法中正确的是（ B ）
（A）从枪膛中飞出的子弹，在惯性力作用下飞行
（B）满载的卡车比空车难以停下来，是因为前者的惯性比后者大
（C）一个运动物体在粗糙水平路面上比光滑水平路面上难以起动，是因为在前一种情况下惯性大
（D）喷气式飞机起飞后越飞越快，说明它的惯性越来越大
4
5班：96%；6班：96%
关于力的分解，下列说法中正确的是（ C ）
（A）一个力只能分解为两个分力
（B）分力的大小必定小于被分解的这个力
（C）通常按力的作用效果来分解力
（D）一个力分解为两个共点力，只能有一种结果
5
5班：84%；6班：88%
如图所示，舰载机保持牵引力F大小不变在匀速航行的航母上降落时受到阻拦而静止，此时阻拦索夹角θ＝120°，空气阻力和甲板阻力不计，则每根阻拦索的拉力大小为（ B ）
（A）\(\frac{F}{2}\) （B）F （C）\(\sqrt{3}F\) （D）2F
6
5班：84%；6班：68%
\(T\)
\(F\)
\(T\)
足球运动员已将足球踢向空中，如图所示，下列描述足球在向斜上方飞行过程中某时刻的受力图中，正确的是（G为重力，F为脚对球的作用力、F阻为阻力）（ B ）
7
5班：100%；6班：88%
粗糙的水平地面上有一木箱。现用一水平力拉着木箱匀速前进，则（B ）
（A）木箱所受的拉力和地面对木箱的摩擦力是一对作用力和反作用力
（B）木箱对地面的压力和地面对木箱的支持力是一对作用力和反作用力
（C）木箱所受的重力和地面所受的压力是一对平衡力
（D）木箱对地面的压力和地面对木箱的支持力是一对平衡力
8
5班：72%；6班：88%
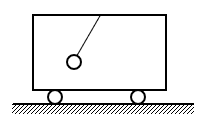
如图，一小球通过细绳悬挂于车厢顶上，车厢在水平轨道上做直线运动，小球相对车厢静止，则下列对车厢运动情况的描述正确的是（ C ）
（A）一定向右加速 （B）一定向左加速
（C）可能向左减速 （D）可能向右匀速
9
5班：80%；6班：88%
\(T\)
\(G\)
\(a\)
对于自由落体运动下面说法正确的是（D ）。
（A）第1 s内、第2 s内、第3 s内的平均速度之比是1∶2∶3
（B）前1 s内、前2 s内、前3 s内的平均速度之比是1∶3∶5
（C）第1 s末、第2 s末、第3 s末的瞬时速度之比是1∶3∶5
（D）前1 s内、前2 s内、前3 s内的位移比是1∶4∶9
10
5班：80%；6班：96%
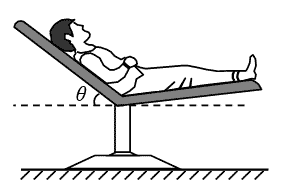
如图所示，某人静躺在椅子上，椅子的靠背与水平面之间有固定倾斜角θ。若此人所受重力为G，则椅子各部分对他的作用力的合力大小为（A ）
（A）G （B）Gsinθ
（C）Gcosθ （D）Gtanθ
11
5班：92%；6班：80%
\(G\)
\(F\)
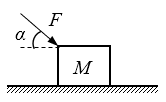
如图所示，位于水平地面上的质量为M的小木块，在大小为F、方向与水平方向成α角的推力作用下沿地面向右作匀加速直线运动，若木块与地面之间的动摩擦因数为μ，则木块的加速度为（ ）
（A）\(\frac{{F\cos \alpha - \mu (Mg + F\sin \alpha )}}{M}\) （B）\(\frac{{F\cos \alpha + \mu (Mg + F\sin \alpha )}}{M}\)
（C）\(\frac{{F\cos \alpha - \mu (Mg - F\sin \alpha )}}{M}\) （D）\(\frac{{F\cos \alpha + \mu (Mg - F\sin \alpha )}}{M}\)
12
5班：72%；6班：80%
\(N\)
\(G\)
\(f\)
\(F\)
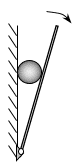
如图，一小球放置在木板与竖直墙面之间。设墙面对球的压力大小为N1，球对木板的压力大小为N2。以木板与墙连接点所形成的水平直线为轴，将木板从图示位置开始缓慢地转到水平位置。不计摩擦，在此过程中（ B ）
（A）N1始终减小，N2始终增大
（B）N1始终减小，N2始终减小
（C）N1先增大后减小，N2始终减小
（D）N1先增大后减小，N2先减小后增大
13
5班：36%；6班：28%
\(N_1\)
\(N_2\)
\(G\)
如果力F在时间t内使质量为m的物体由静止开始移动了一段距离s，那么下述结论中不正确的是（ B ）
（A）质量为m的静止物体，在力2F的作用下，经过t/2 ，移动的距离为s/2
（B）质量为2m的静止物体，在力F的作用下，经过2t，移动的距离为s
（C）质量为m2 的静止物体，在力F的作用下，经过2t，移动的距离为8s
（D）质量为m的静止物体，在力F/2 的作用下，经过t，移动的距离为s/2
14
5班：48%；6班：48%
水平面上的三个共点力大小分别是4 N、6 N、11 N，则它们合力的最大值是21N，最小值是1N。
15
5班：%；6班：92%
1905年相对论的建立，使人们认识到牛顿力学只有在低速、宏观领域中才能适用。
16
5班：%；6班：77%
升降机以0.5 m/s2的加速度加速上升，站在升降机里质量为40 kg的人对升降机地板的压力为420N；如果升降机以相同大小的加速度减速上升，人对地板的压力又为380N。（g＝10 m/s2）
17
5班：%；6班：79%
17．在地球上做自由落体运动的物体，着地速度是20 m/s，则该物体是从20m高处下落的。如果是在月球上则是从120m高处落下的（月球上落体加速度是地球上的1/6 ）。（g取10 m/s2）
18
5班：%；6班：79%
19
5班：%；6班：54%
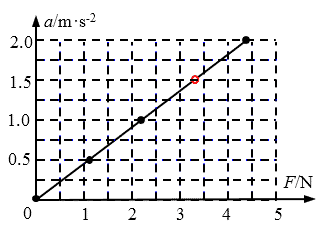
在“用DIS研究加速度与力的关系、加速度与质量的关系”实验中，保持小车质量不变，改变小车所受的作用力，测得了下表所示的5组数据，并已在坐标平面上画出部分数据点，如图所示：
（1）在图中画出第4组数据对应的数据点，然后作出a-F的关系图线；
（2）由所作图线可以得到结论：在质量一定的情况下，加速度a与作用力F成正比；图线的斜率代表的物理量为小车质量的倒数。
（3）当研究加速度与质量的关系时，应保持小车所受所用力不变，改变小车的质量来进行实验。为了直观地判断加速度a与质量m的数量关系，应作a-1/m图象。
20
5班：%；6班：73%
如图所示，一根细绳一端系于水平地面上，另一端系于竖直墙壁上，在绳上O点处竖直向上加一个拉力大小为F，OA与水平面夹角为θ，绳OB垂直于墙壁，此时处于平衡状态。
（1）求绳OA、绳OB对O的拉力大小；（力图1分）
（2）如果F的大小不变，方向改为垂直于OA斜向左上方，并保持OB仍垂直于墙壁，求绳OA、绳OB受到的拉力大小。（力图1分）
F_{OA}=\frac{F}{tan\theta} \newline
F_{OB}=\frac{F}{sin\theta}
F_{OA}=\frac{F}{sin\theta} \newline
F_{OB}=\frac{F}{tan\theta}
\(F_{OB}\)
\(F\)
\(F_{OA}\)
\(F_{OB}\)
\(F\)
\(F_{OA}\)
21
5班：%；6班：44%
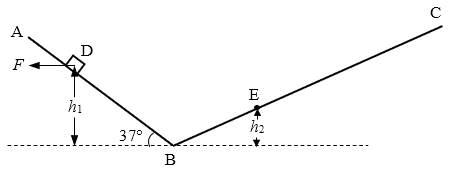
如图，ABC为一竖直面内的光滑轨道，AB段和BC段均为直线，且在B处平滑连接，AB段与水平面的夹角为37°，BC段与水平面的夹角为30°。D、E是轨道上的两点，D点的高度h1＝0.6 m。质量m＝1.6 kg的小物体，受水平向左的恒力F的作用，从D点由静止开始，沿AB向下做匀加速直线运动。当物体运动到B点时撤去F，此时的速度vB=2 m/s，然后物体继续沿BC段斜向上运动，至E点时速度为零。求：（sin37°＝0.6，cos37°＝0.8，g取10 m/s2）
（1）物体在AB段运动时加速度a1的大小；
（2）物体所受恒力F的大小。（力图1分）
牛顿定律中使用正交分解法时，x轴必须TMD沿a方向
21
5班：%；6班：44%
如图，ABC为一竖直面内的光滑轨道，AB段和BC段均为直线，且在B处平滑连接，AB段与水平面的夹角为37°，BC段与水平面的夹角为30°。D、E是轨道上的两点，D点的高度h1＝0.6 m。质量m＝1.6 kg的小物体，受水平向左的恒力F的作用，从D点由静止开始，沿AB向下做匀加速直线运动。当物体运动到B点时撤去F，此时的速度vB=2 m/s，然后物体继续沿BC段斜向上运动，至E点时速度为零。求：（sin37°＝0.6，cos37°＝0.8，g取10 m/s2）
（3）物体在BC段运动时加速度a2的大小；（力图1分）
（4）E点的高度h2。
牛顿定律中使用正交分解法时，x轴必须TMD沿a方向
第三章 牛顿运动定律
By fjphysics
