Primordial Black Hole Formation by a Spherical Domain Wall
Heling Deng
· Introduction
· Simulation
· Results
Introduction
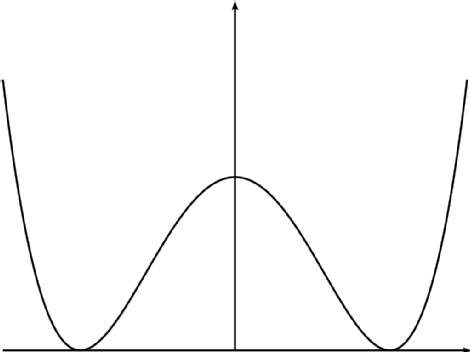
\phi
V(\phi)
Ipser & Sikivie (1984)
Minkowski
Schwarzschild
Blau, Guendelman & Guth (1987)
de Sitter
Schwarzschild
FRW
FRW
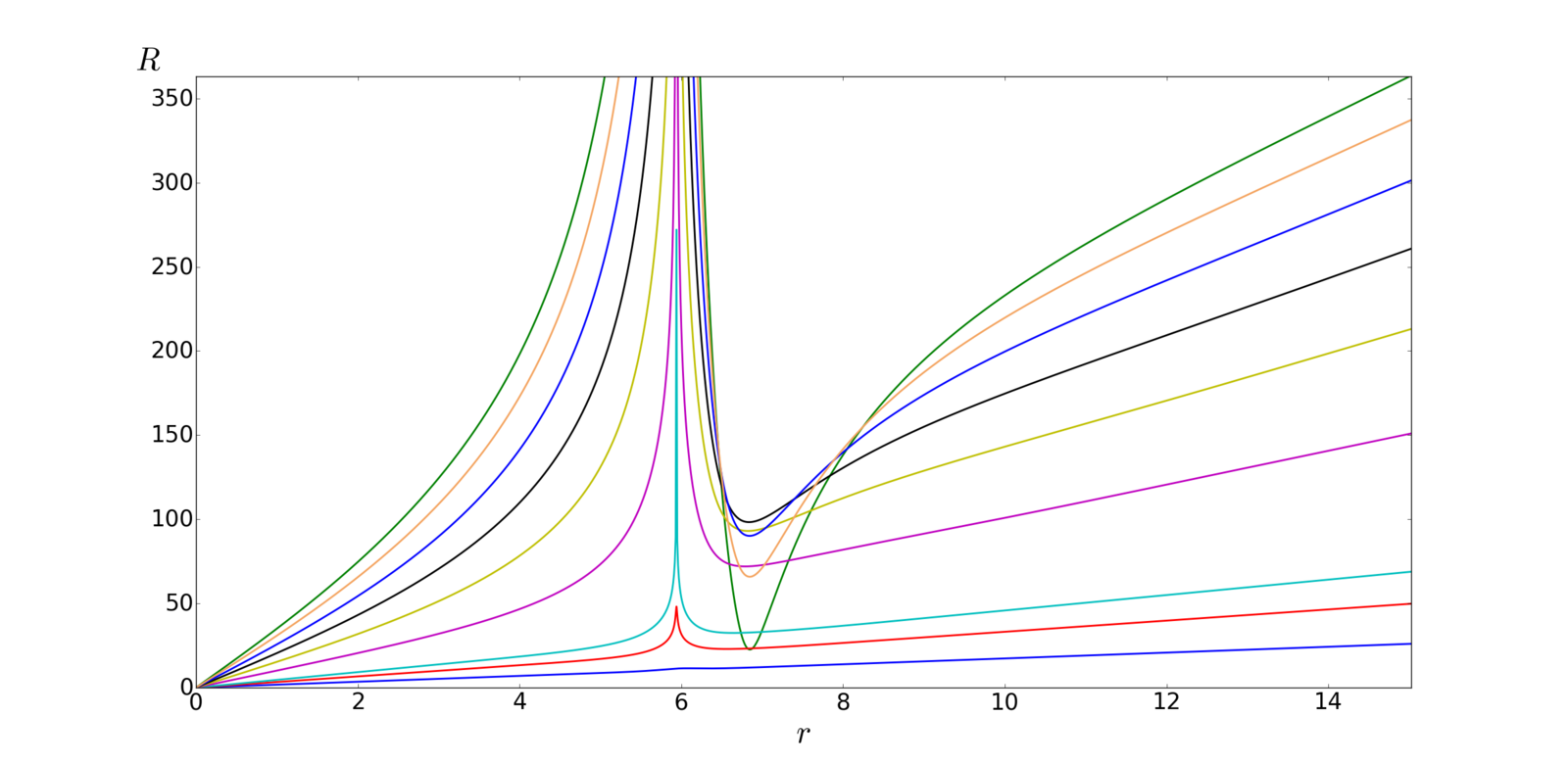
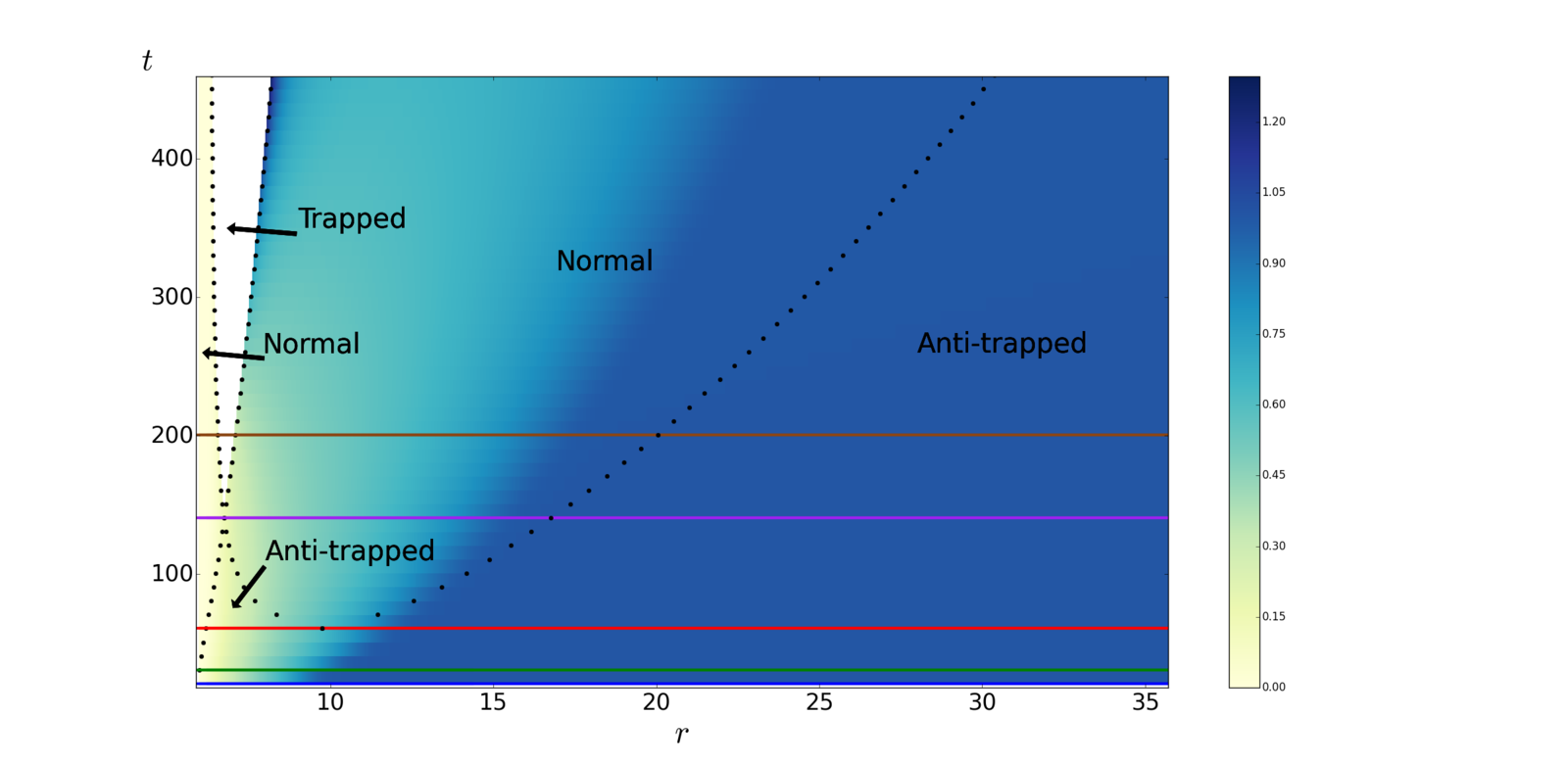
- Two characteristic time scales
t_{\sigma}=\frac{1}{2\pi\sigma}
ds^{2}=-\left(1-\frac{\left|x\right|}{t_{\sigma}}\right)^{2}dt^{2}+dx^{2}+\left(1-\frac{\left|x\right|}{t_{\sigma}}\right)^{2}e^{2t/t_{\sigma}}\left(dy^{2}+dz^{2}\right)
1. Wall expansion
2. Cosmological expansion
t_{H}=\frac{8r_{i}^{3}}{27t_{i}^{2}}
(dust)
t_{H}=\frac{r_{i}^{2}}{4t_{i}}
(radiation)
Hubble crossing
ar_i=\frac{1}{H}
(\sigma)
(r_i)
- Two parameters:
\sigma,\ r_i
where
- Critical behavior
t_{\sigma}\gg t_{H}
1. Subcritical
2. Supercritical
t_{\sigma}\ll t_{H}
Collapses
Grows without bound
Wormhole
BH
BH
- Matching on the wall
\ddot{r}+(4-3a^{2}\dot{r}^{2})H\dot{r}+\frac{2}{a^{2}r}(1-a^{2}\dot{r}^{2})=6\pi\sigma\frac{(1-a^{2}\dot{r}^{2})^{\frac{3}{2}}}{a}
EOM:
FRW +
ds^{2}=-dt^{2}+B^{2}(r,t)dr^{2}+R^{2}(r,t)d\Omega^{2}
Dust
Radiation
Simulation
- Metric
ds^{2}=-dt^{2}+B^{2}dr^{2}+R^{2}d\Omega^{2}
- Energy-momentum tensor
T_{\nu}^{(\phi)\mu}=\partial^{\mu}\phi\partial_{\nu}\phi-\delta_{\nu}^{\mu}\left[\frac{1}{2}(\partial \phi)^{2}-V(\phi)\right]
T_{\nu}^{(f)\mu}=\left(\rho+p\right)u^{\mu}u_{\nu}-\delta_{\nu}^{\mu}p
u^{\mu}=\left(\frac{1}{\sqrt{1-v^{2}}},\frac{v}{B\sqrt{1-v^{2}}},0,0\right)
- Variable transformations
r\to\frac{r}{H_{i}},\ t\to\frac{t}{H_{i}},\ \rho\to M_{Pl}^{2}H_{i}^{2}\rho,\ \phi\to M_{Pl}\phi,\ V\to M_{Pl}^{2}H_{i}^{2}V
- Einstein equations + KG equation
B, R, \phi, \rho, v
- Initial and boundary conditions
- BH apparent horizon
\Theta_{out}\propto\frac{\dot{R}+\frac{R^{\prime}}{B}}{R},\ \Theta_{in}\propto\frac{\dot{R}-\frac{R^{\prime}}{B}}{R}
\Theta_{out}=0,\ \Theta_{in}<0
- Misner-Sharp mass
M=\frac{R}{2}(1-\frac{R^{\prime2}}{B^{2}}+\dot{R}^{2})
- Expansions of radial null geodesics
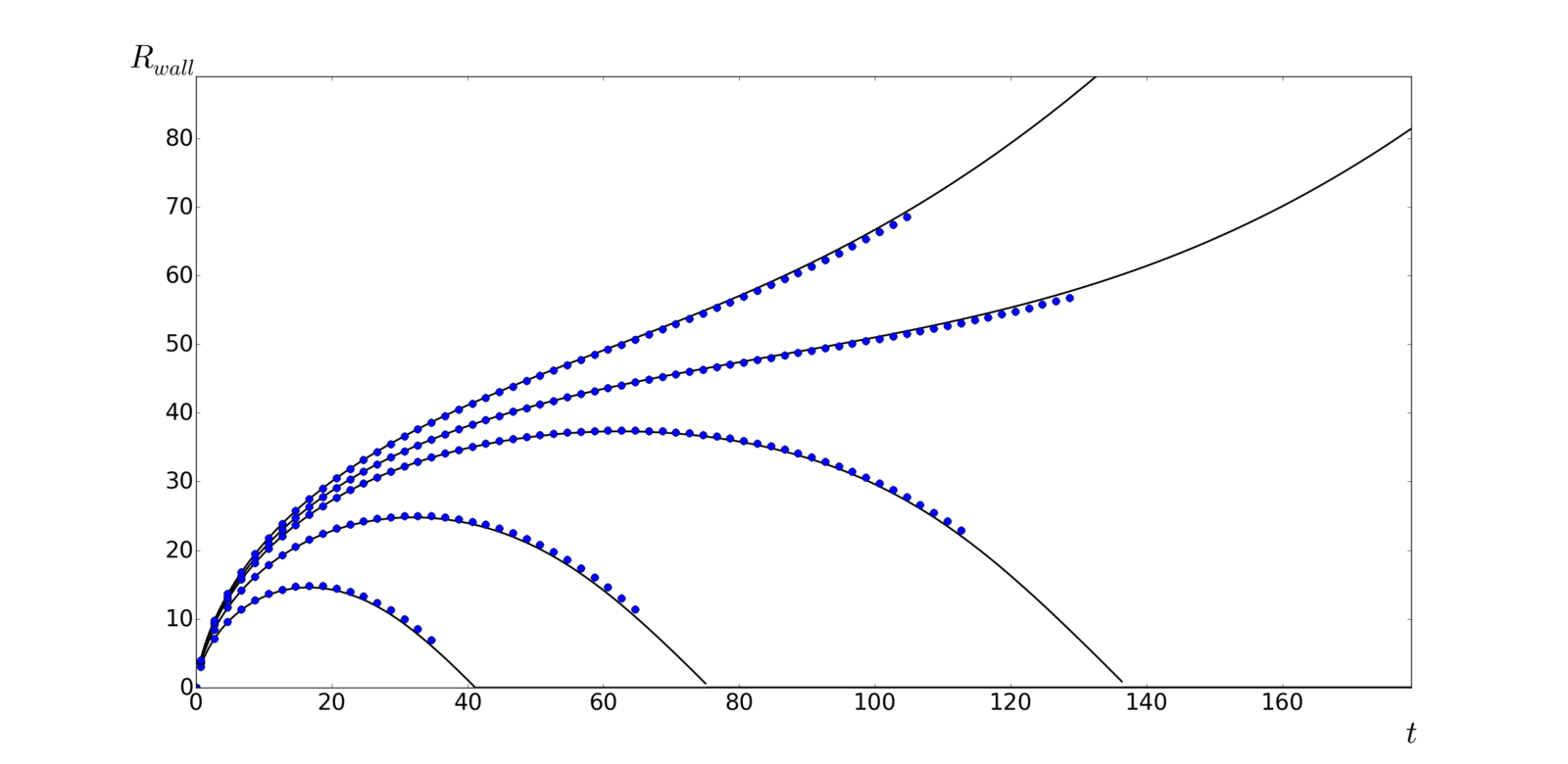
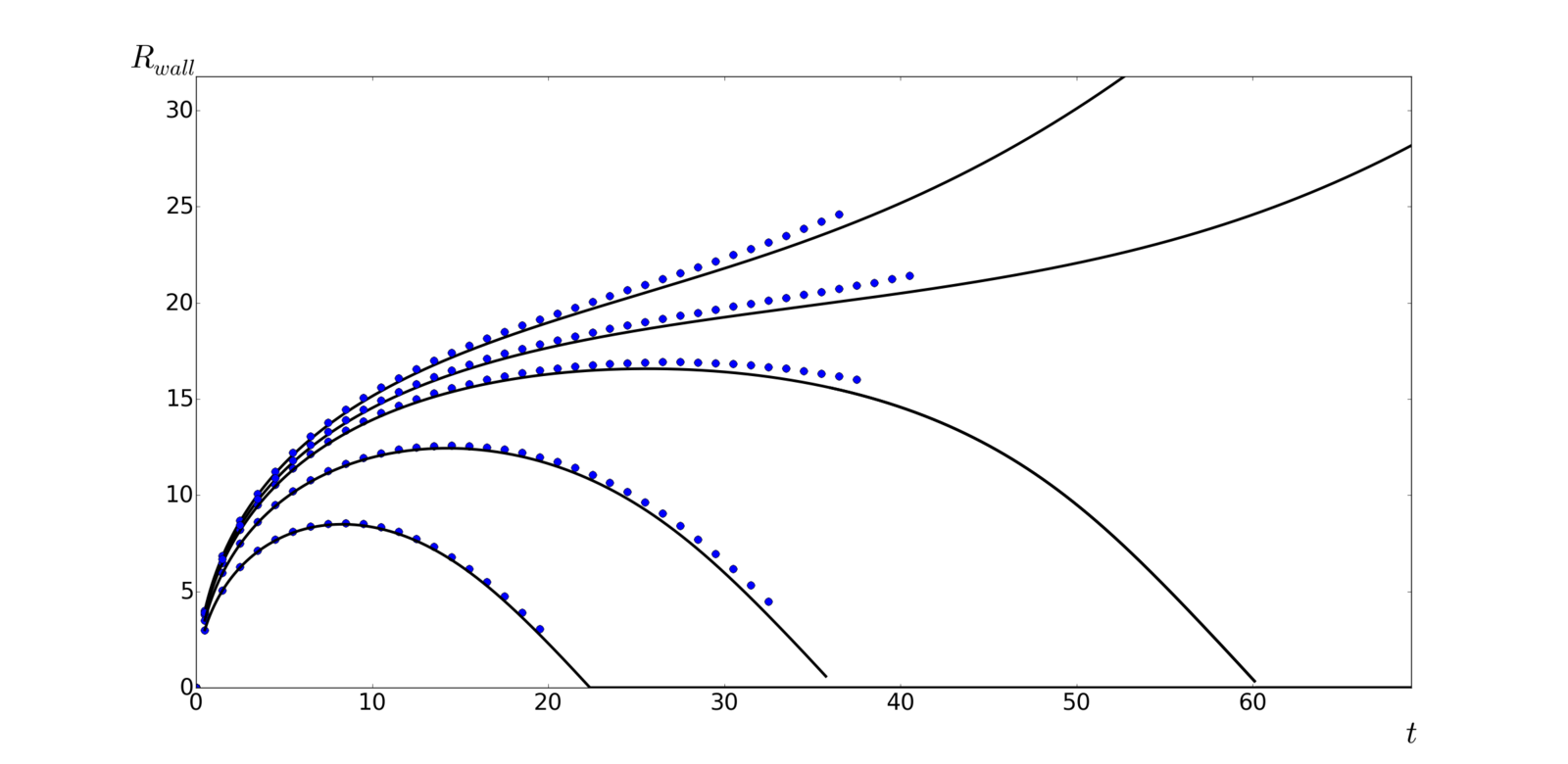
Subcritical wall
- Initial BH mass
M_{BHi}=4\pi\sigma CR_{H}^{2}
where
R_{H}=\frac{1}{H(t_{H})}
C_{dust}\approx0.2,\ C_{radiation}\approx0.6
Garriga, Vilenkin, Zhang (2016)
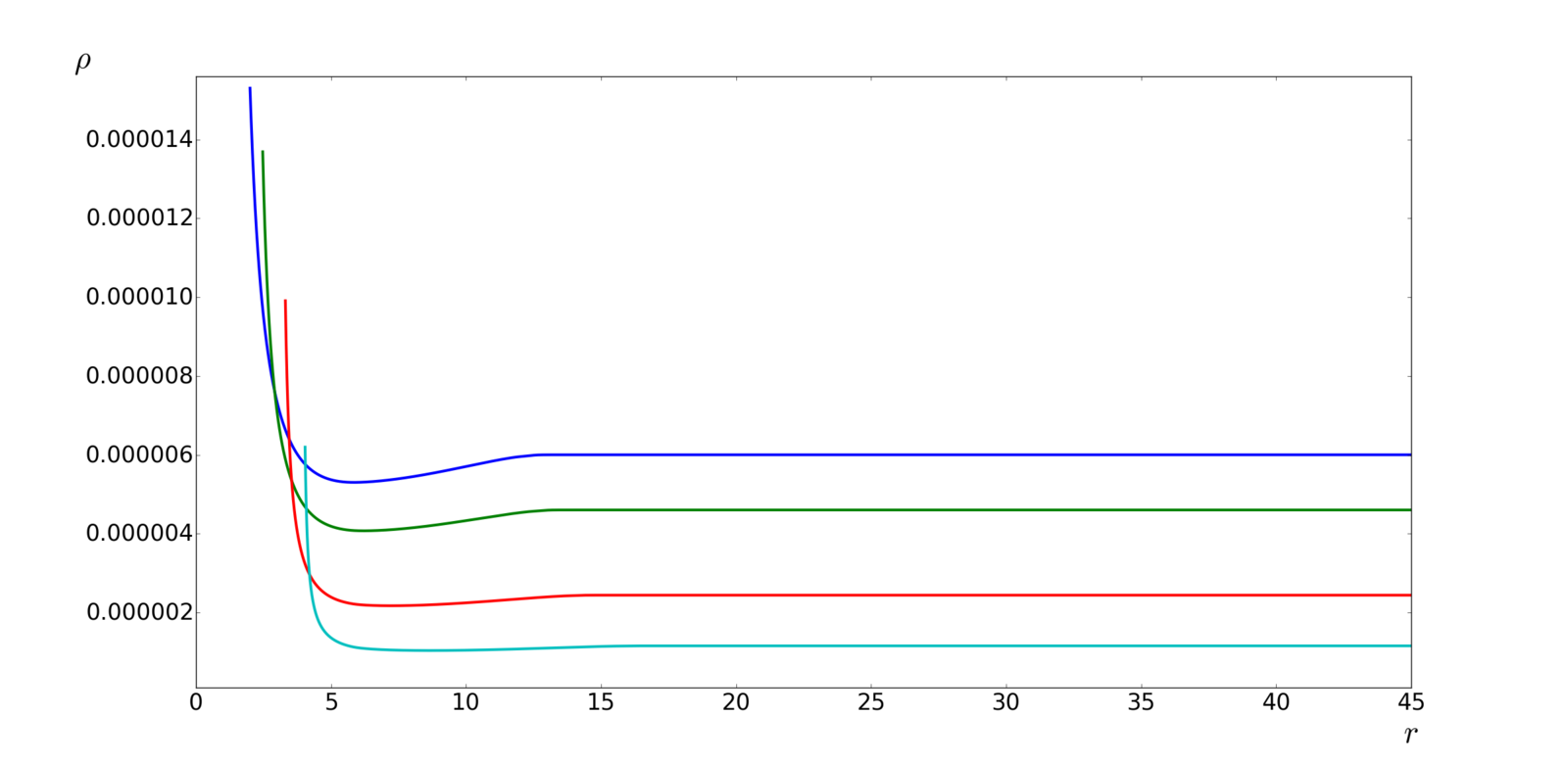
Dust
Radiation
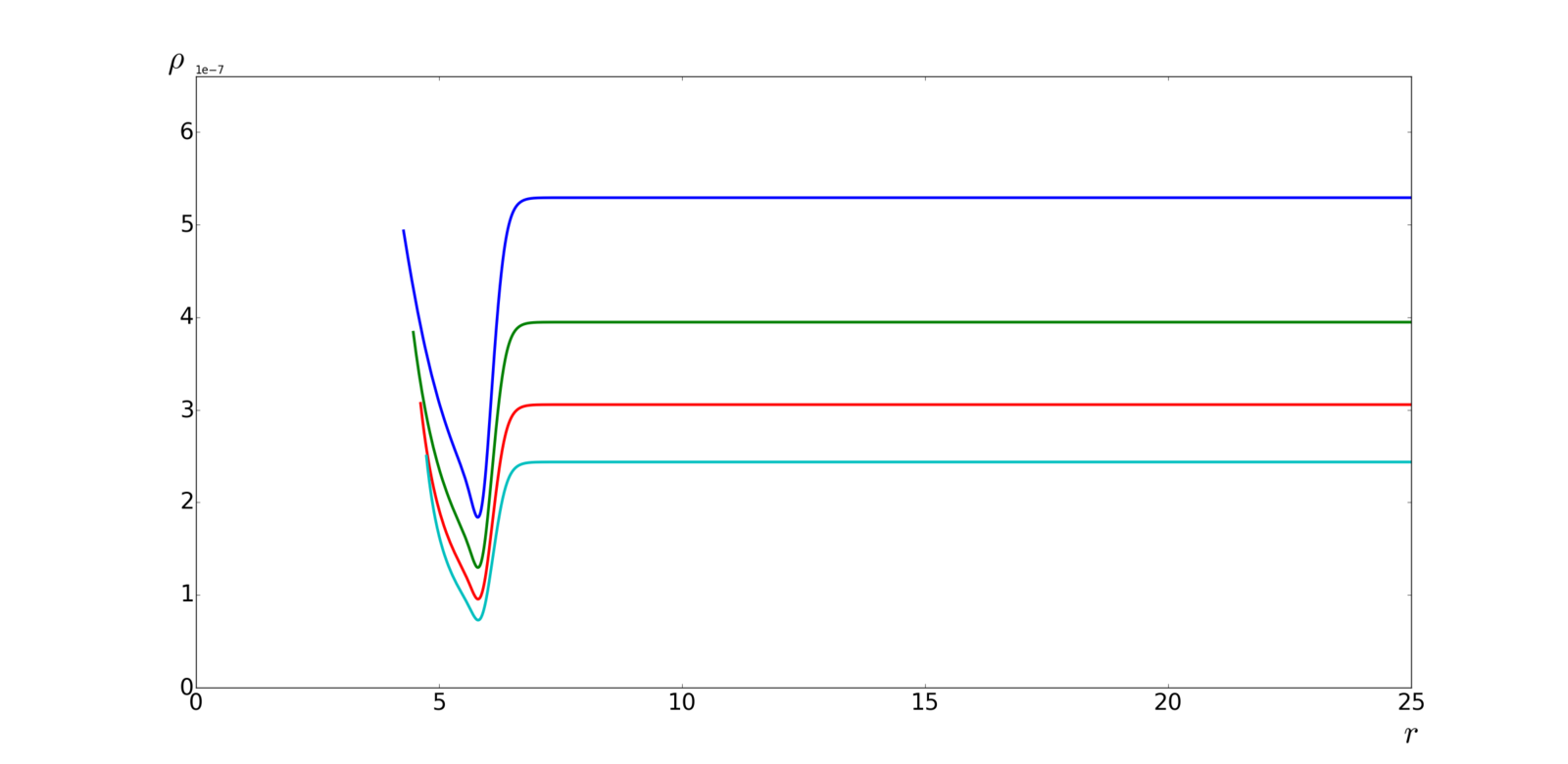
- after BH excision
\rho
Dust
Radiation
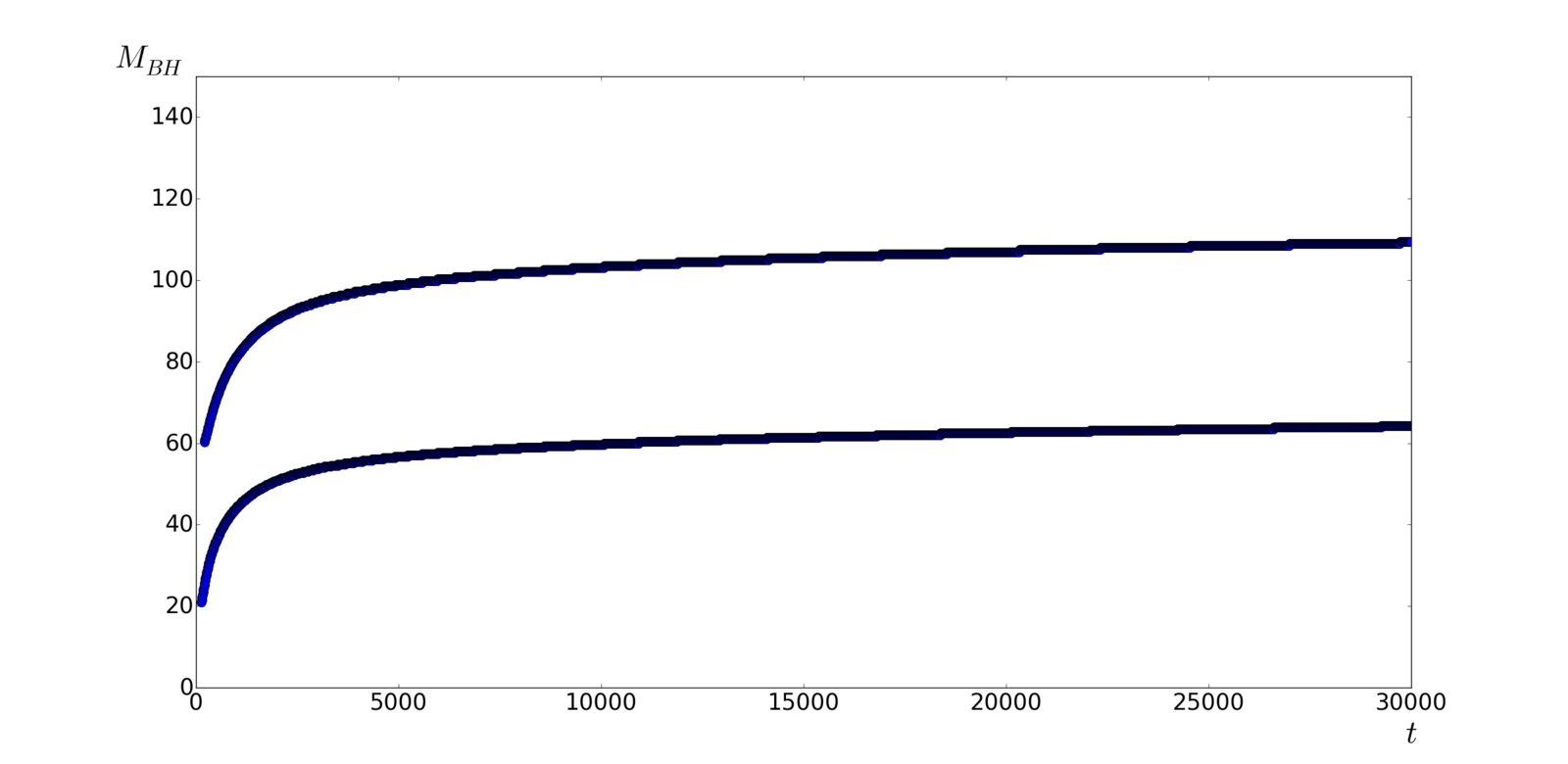
- BH mass evolution
M_{BHf} = M_H = \frac{1}{2}r_i^3
M_{BHf} =\ ?
- Final BH
\frac{dM_{BH}(t)}{dt}=4\pi FR^{2}_{BH}\rho(t)
M_{BH}(t)=\frac{1}{\frac{1}{M_{0}}+\frac{3}{2}F\left(\frac{1}{t}-\frac{1}{t_{0}}\right)}
M_{BHf}=\frac{1}{\frac{1}{M_{0}}-\frac{5.7}{t_{0}}}

F\approx 3.8
Supercritical wall
- Fluid pushed away
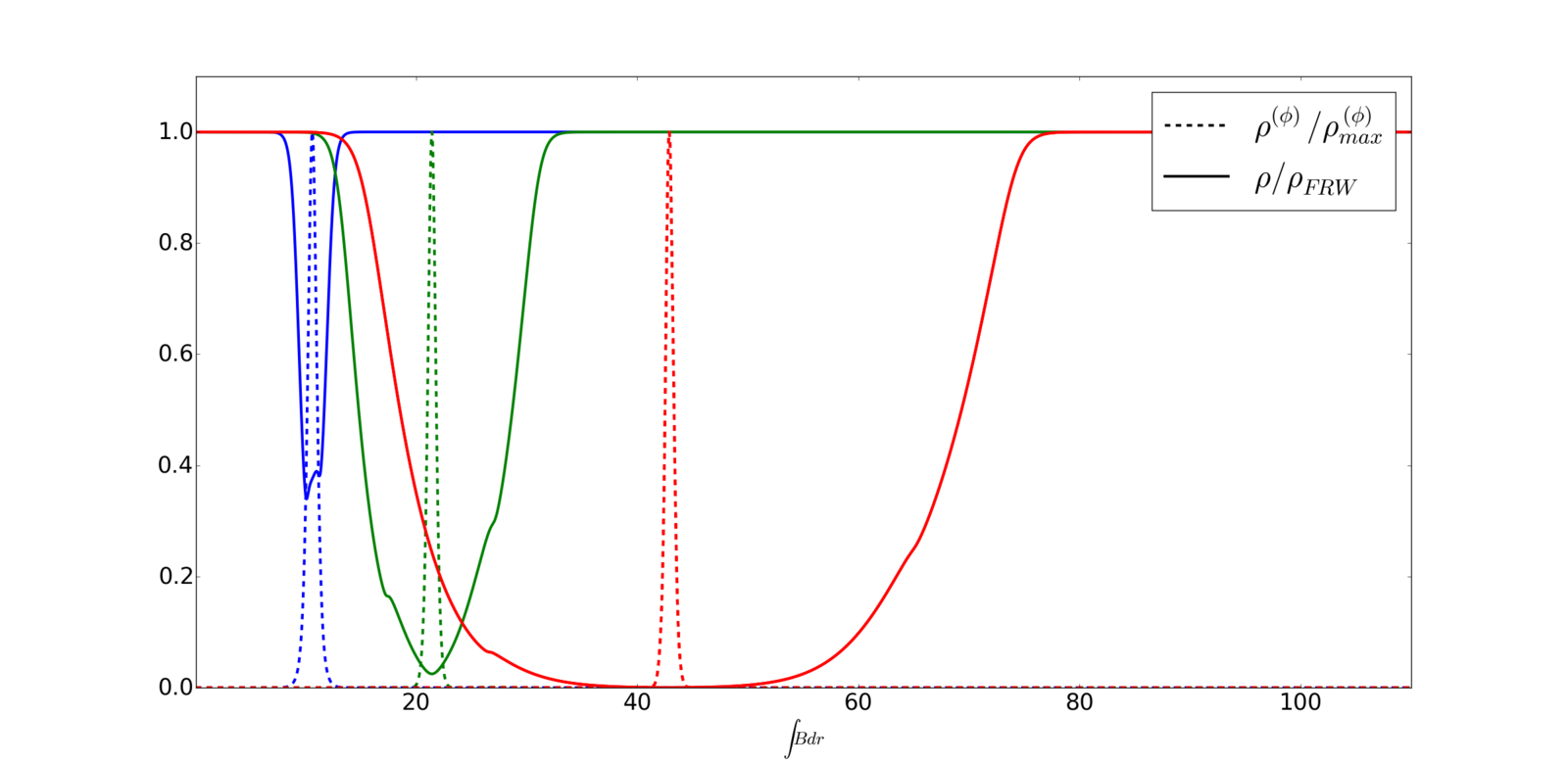
- Singularity arises
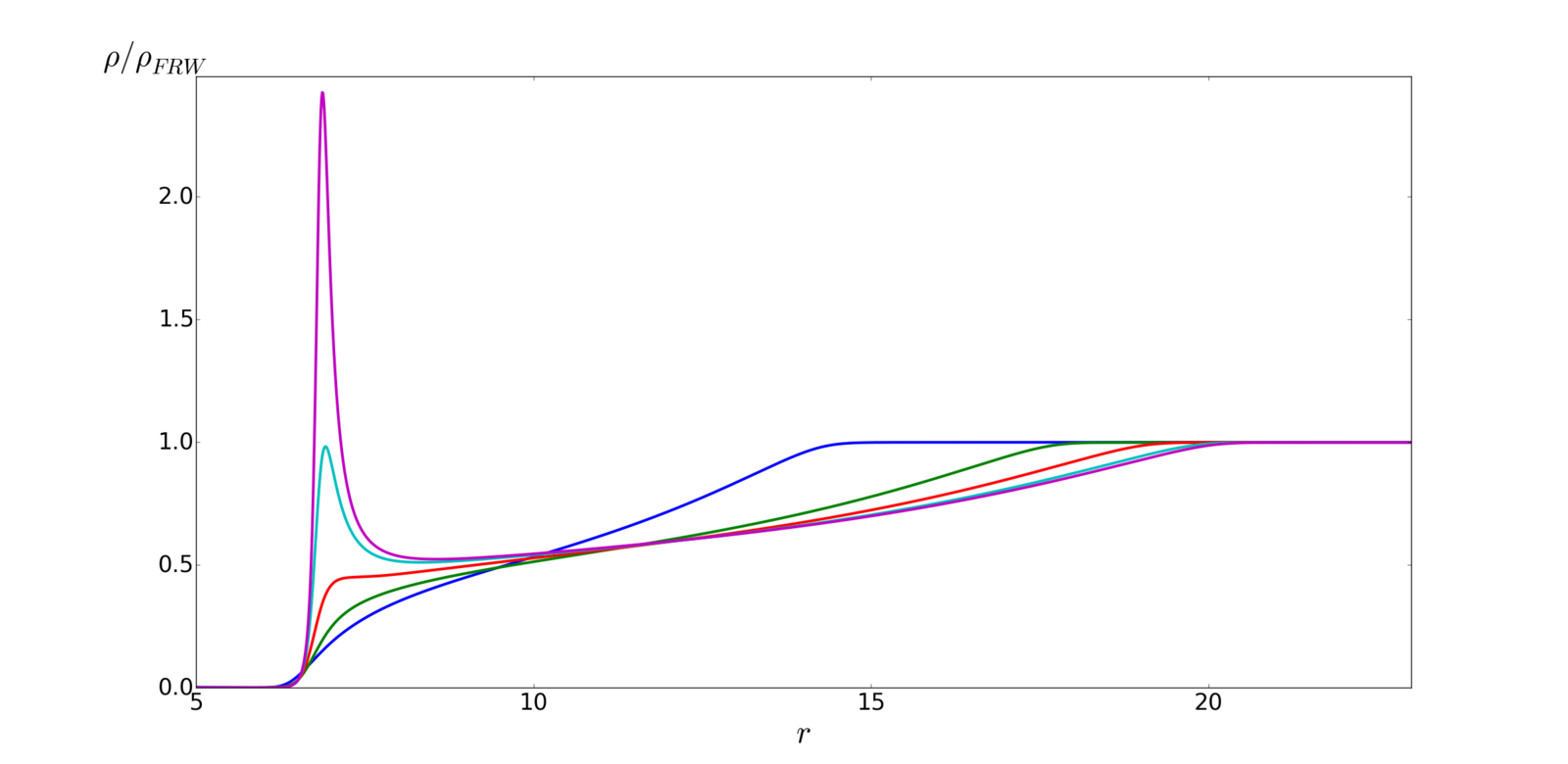
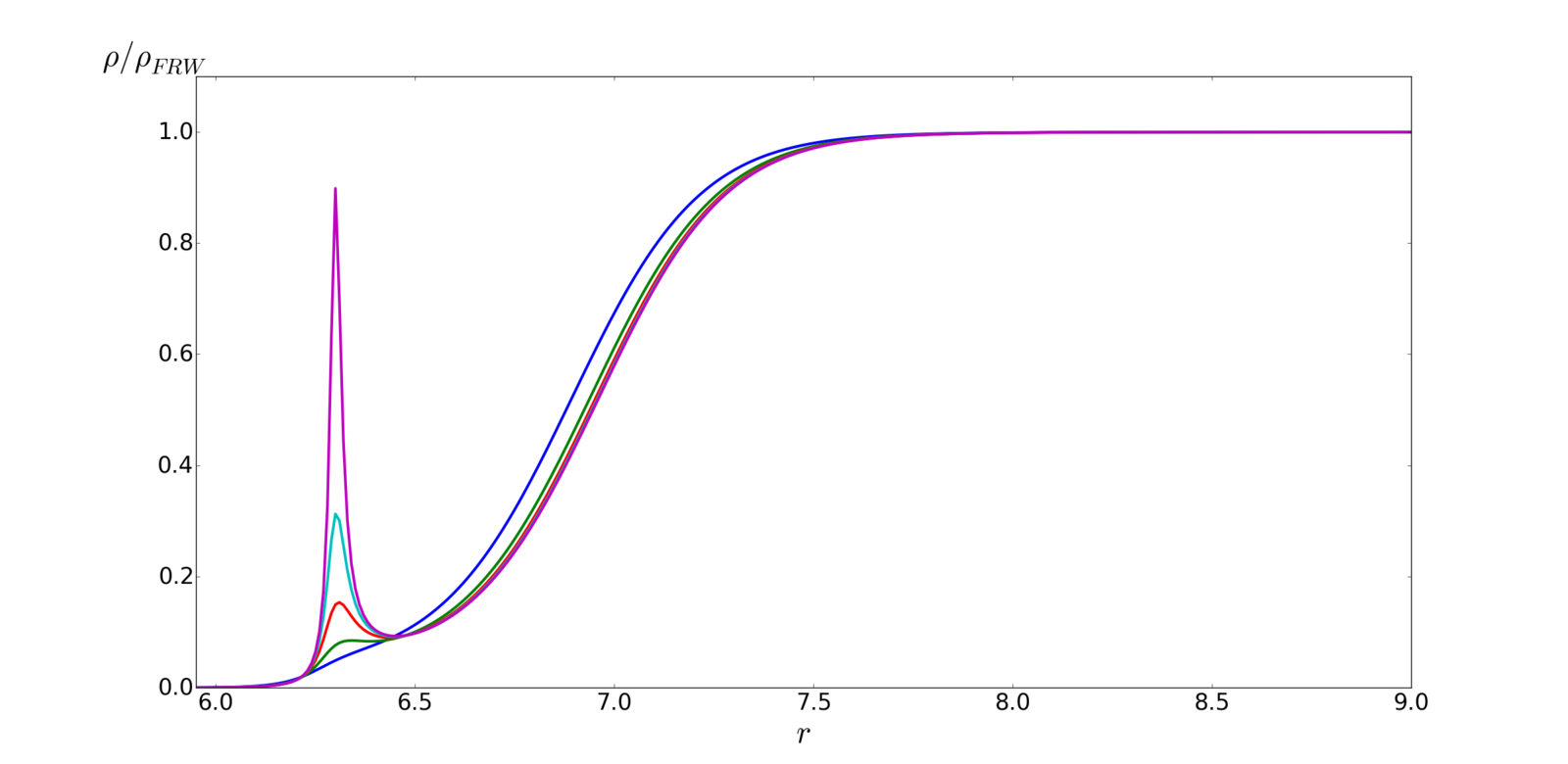
Dust
Radiation
- after BH excision
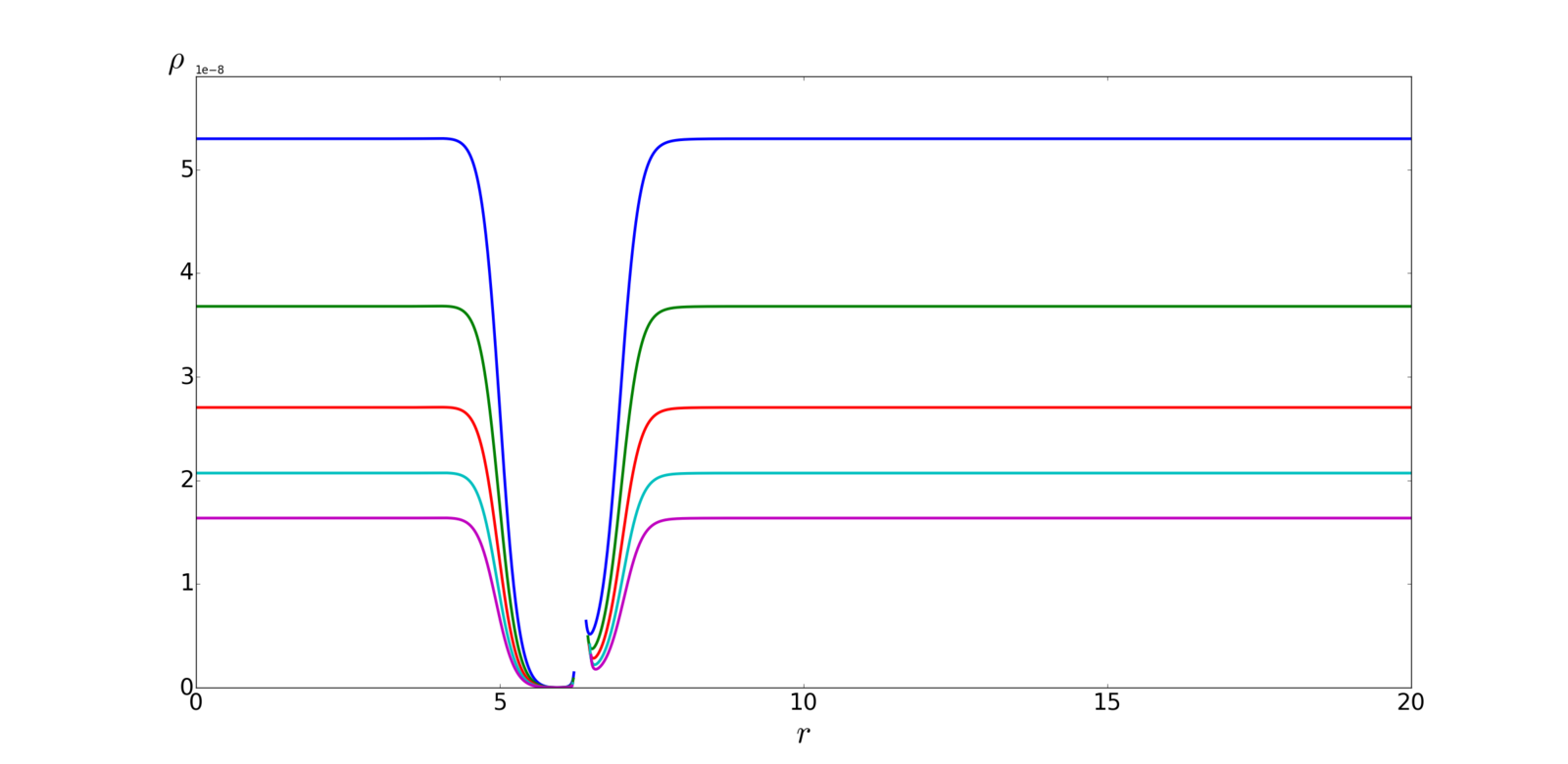
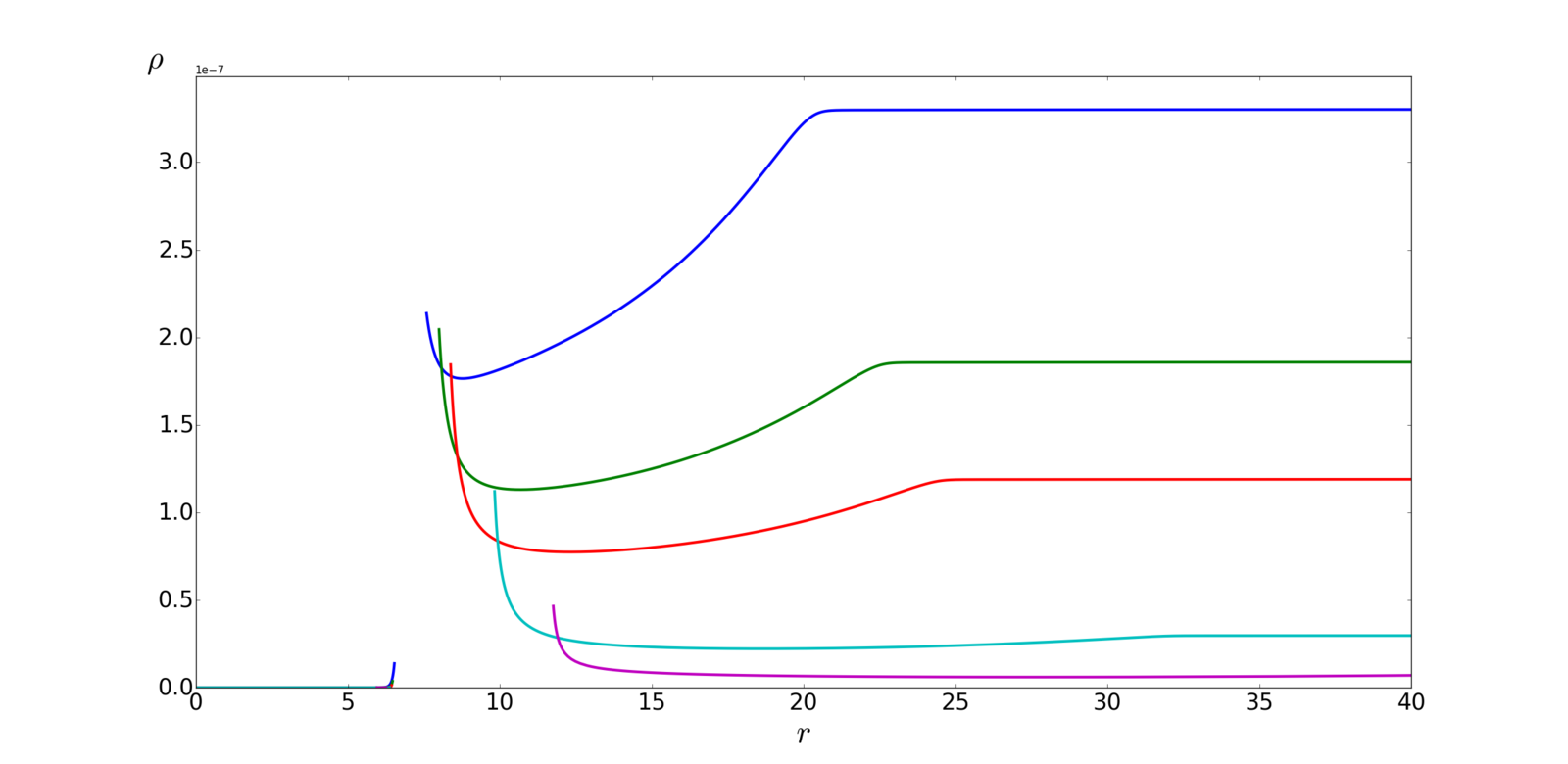
Dust
Radiation
\rho
- Wormhole formation
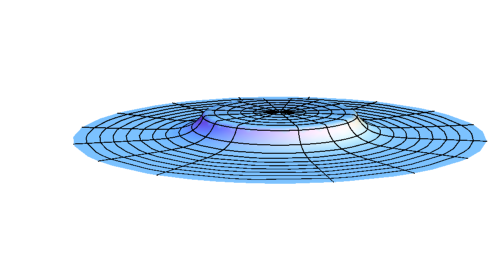
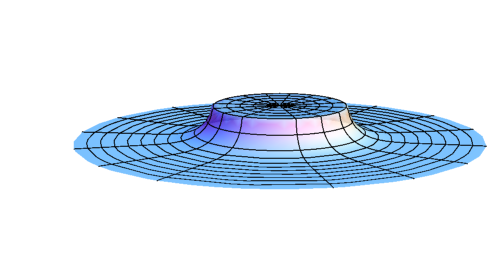
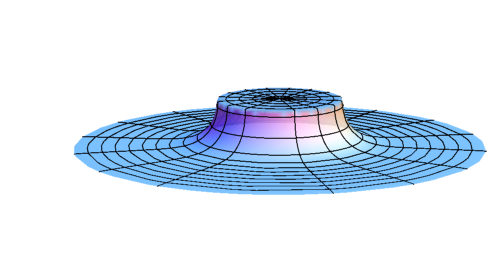
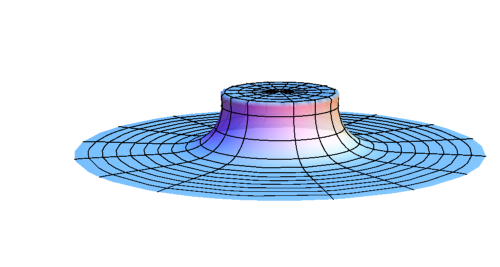
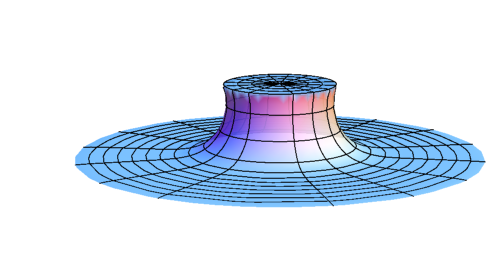
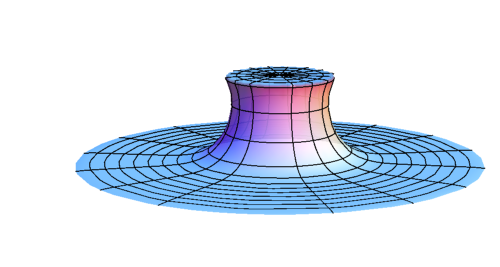
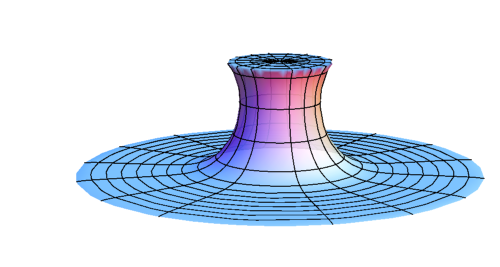
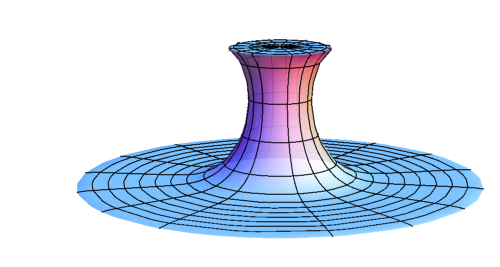
- Spacetime structure
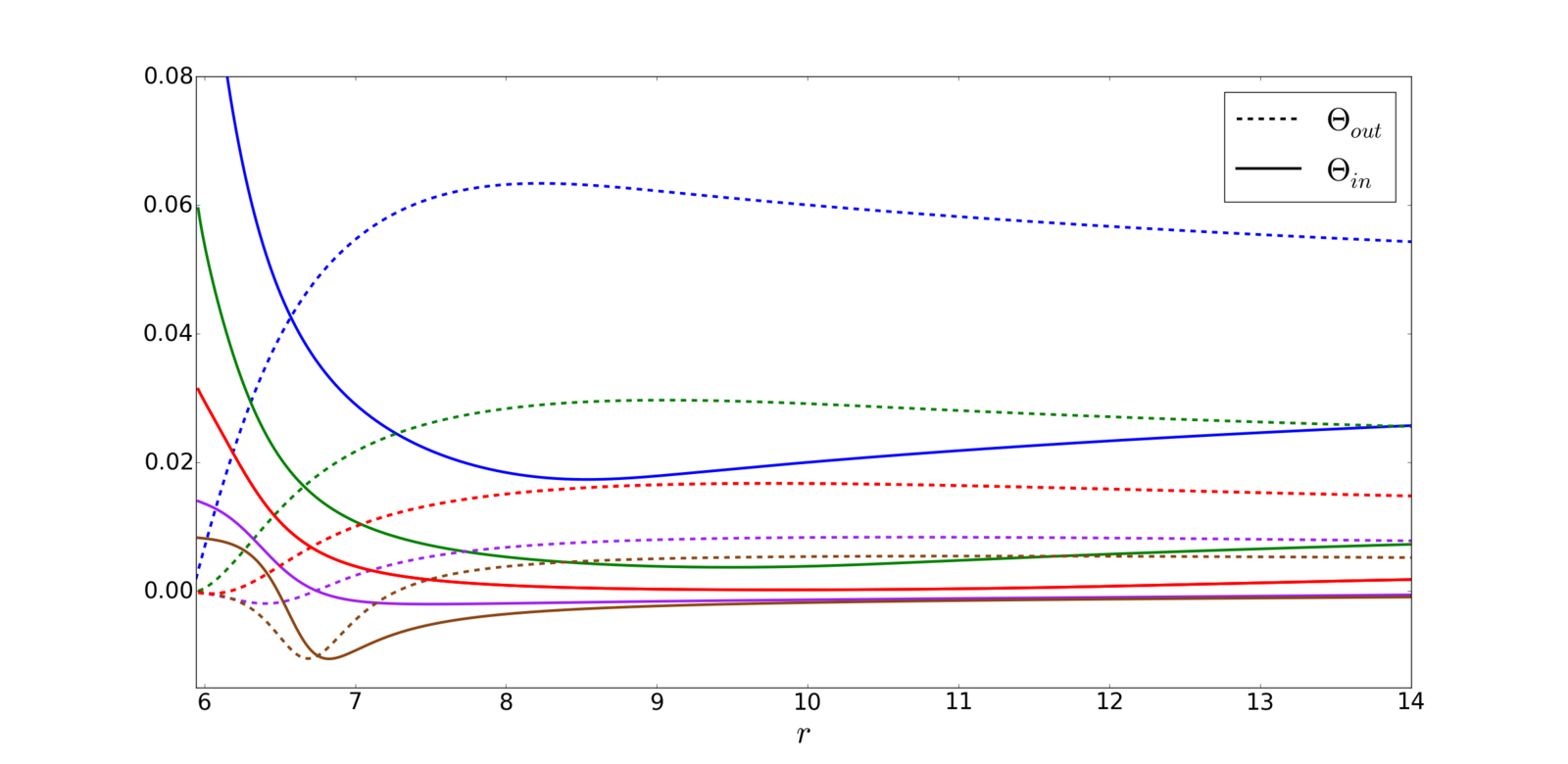
- Spacetime structure
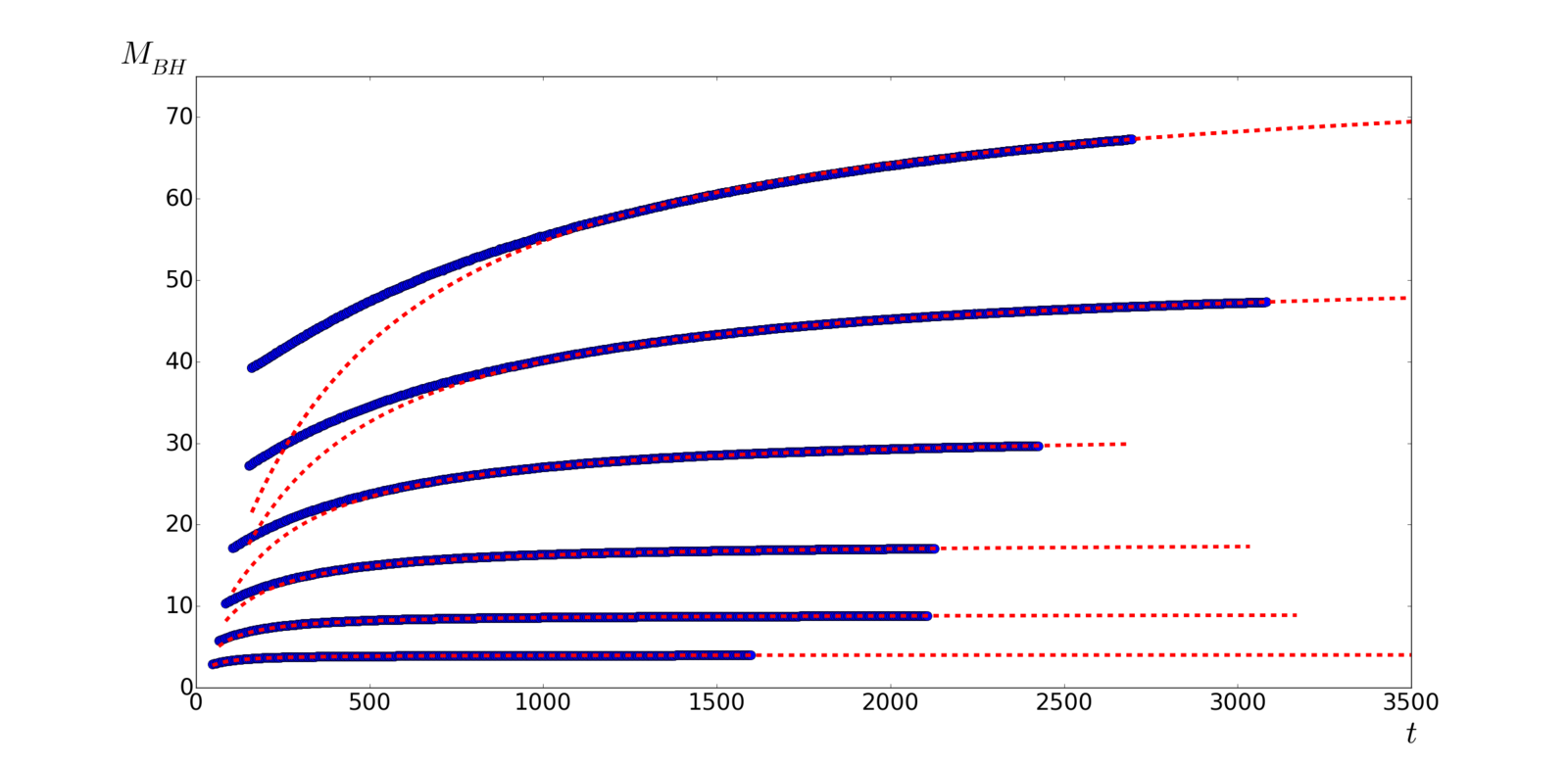
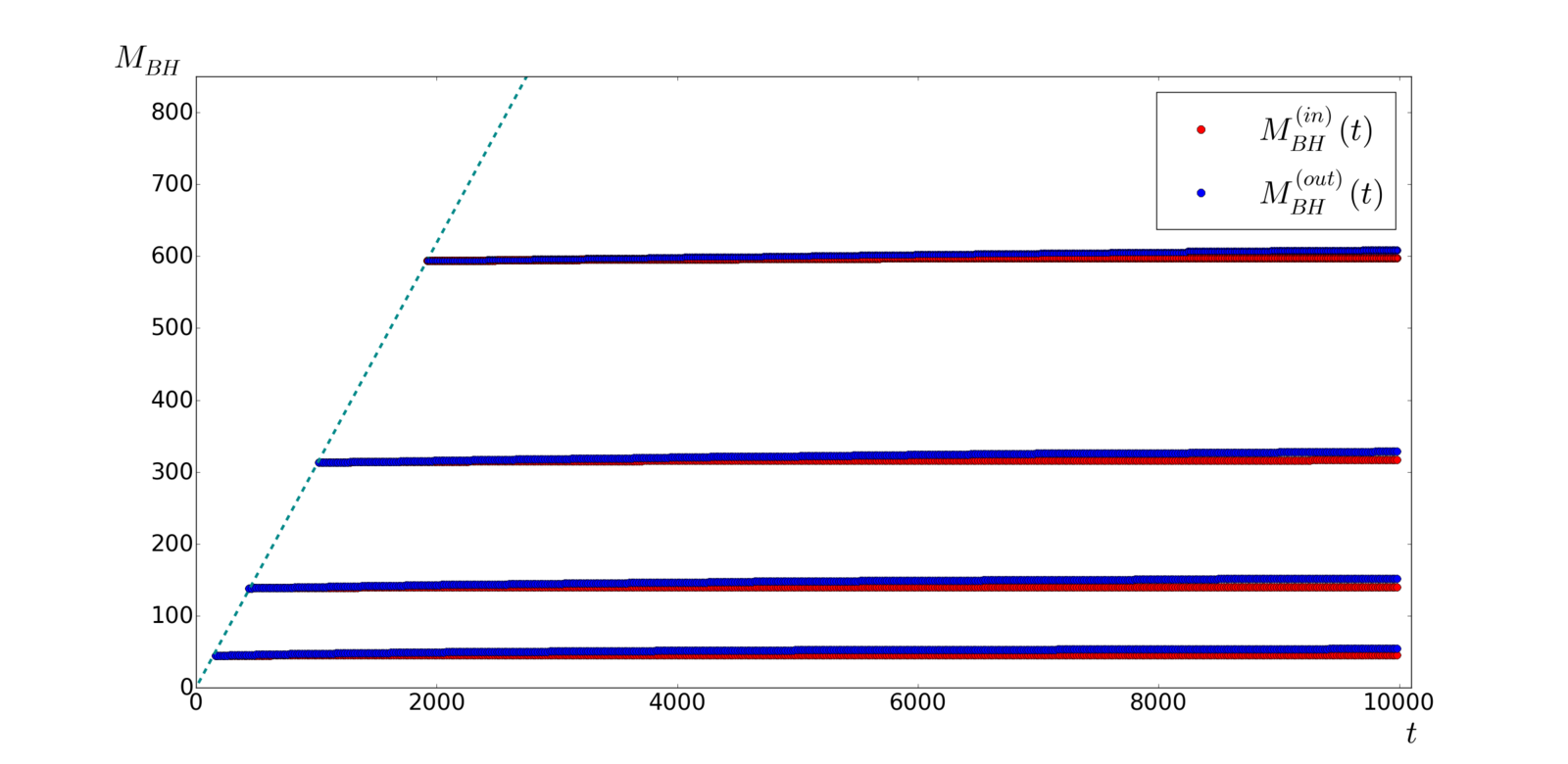
- BH mass evolution
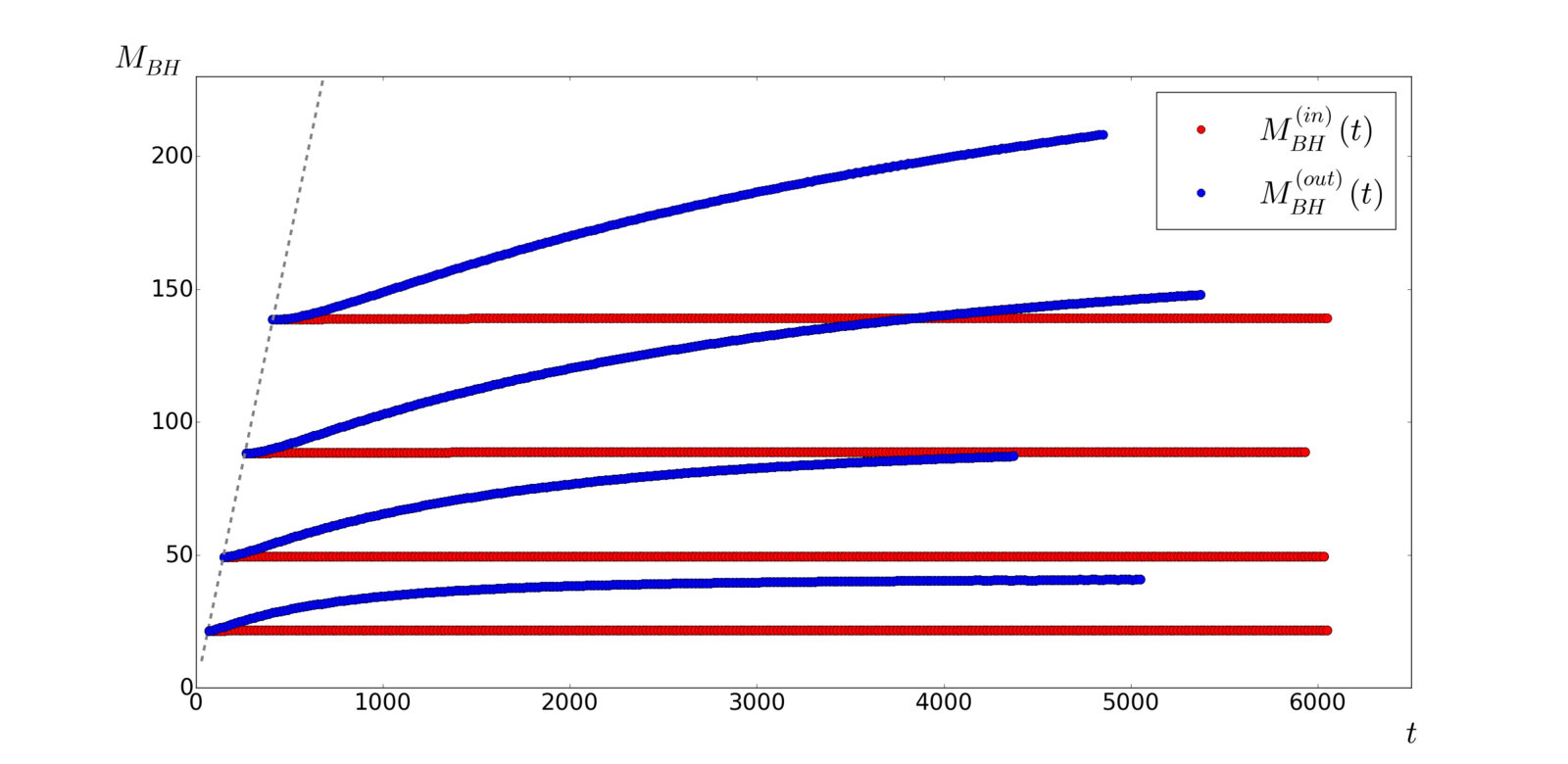
Dust
Radiation
- BH mass in dust universe
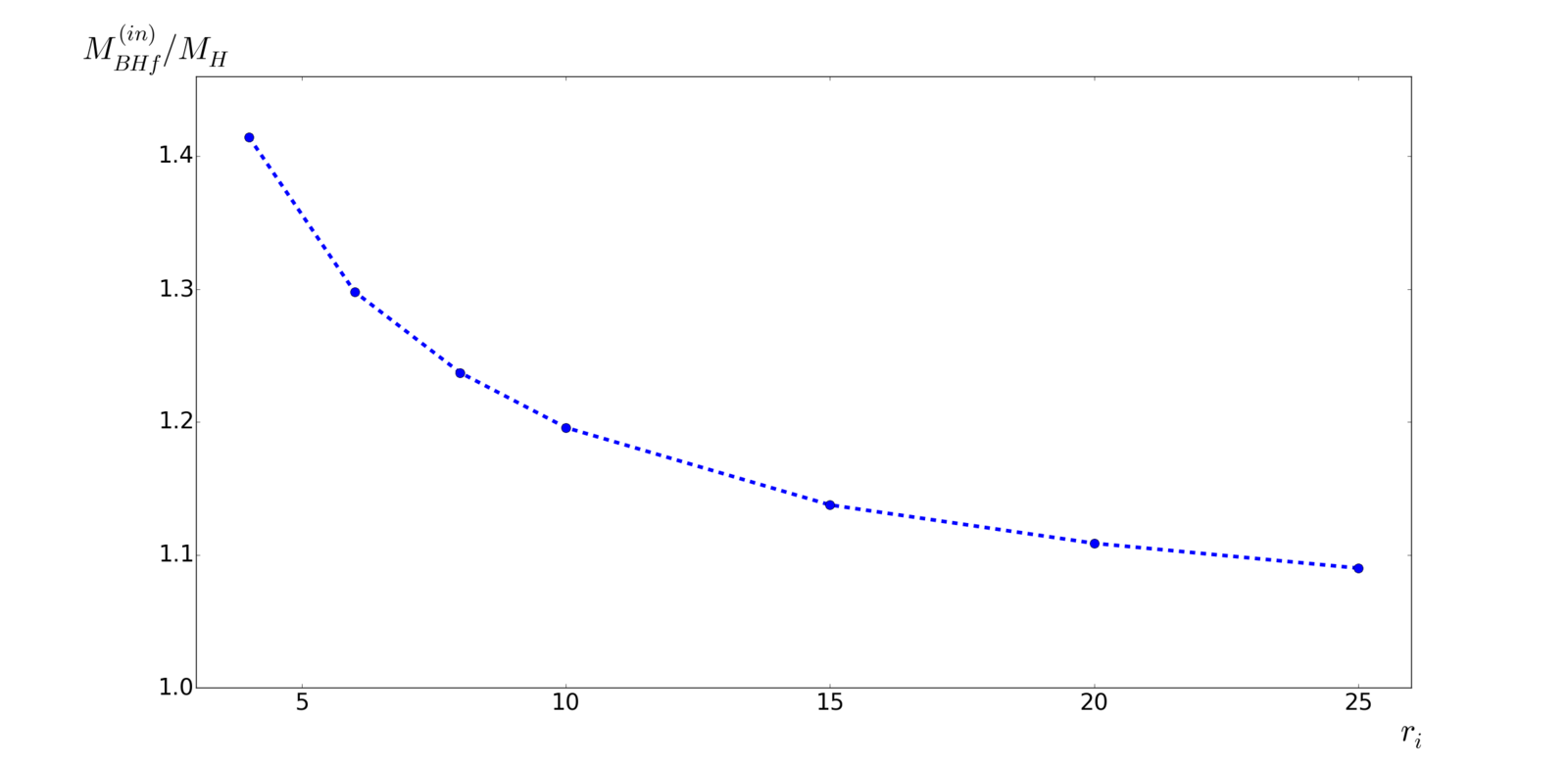
M_{BHf}^{(in)} \approx M_H = \frac{1}{2}r_i^{3}
- Inner BH mass in radiation universe
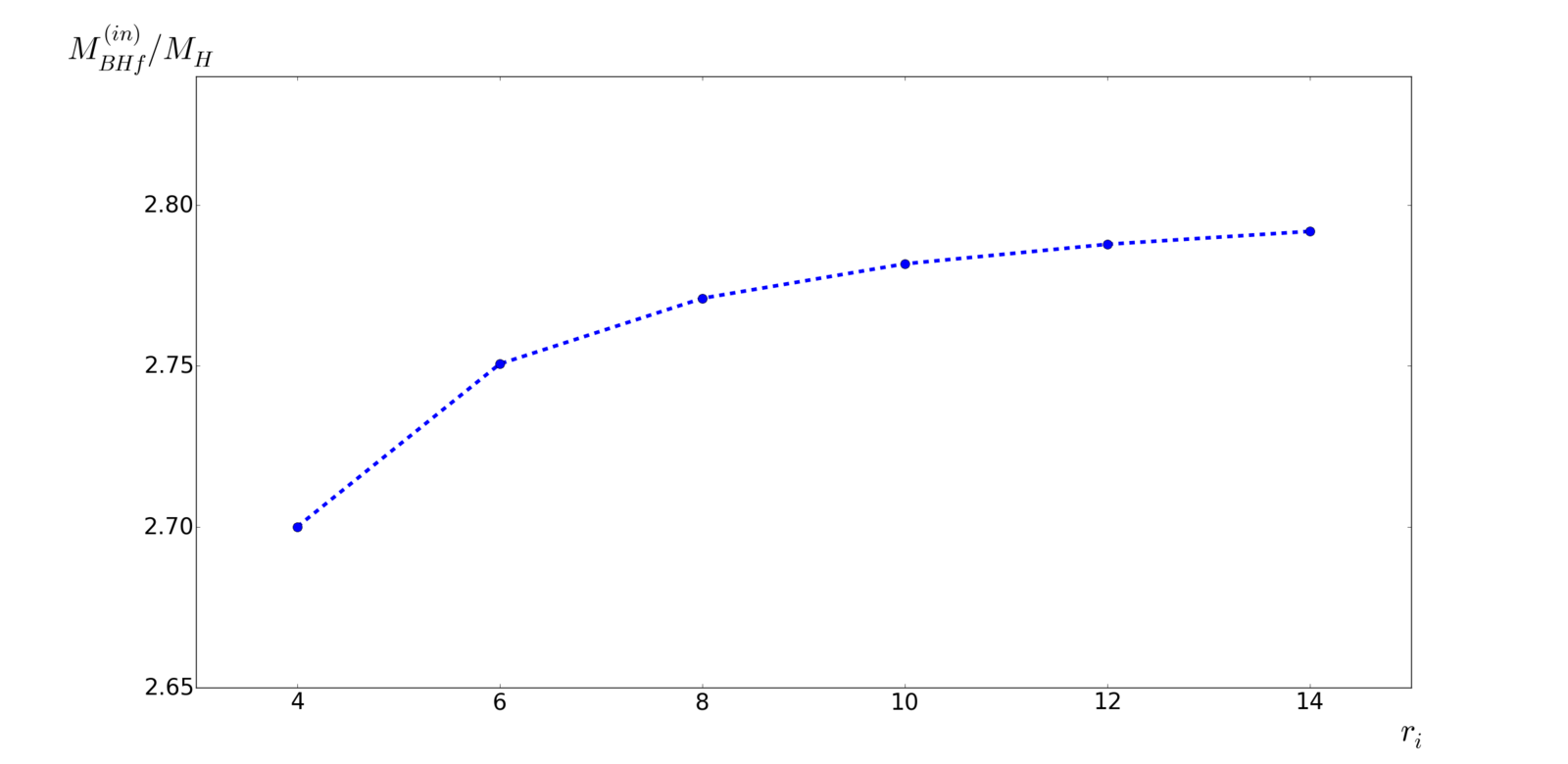
M_{BHf}^{(in)} \approx 2.8 M_H = 1.4 r_i^2
- Outer BH mass in radiation universe
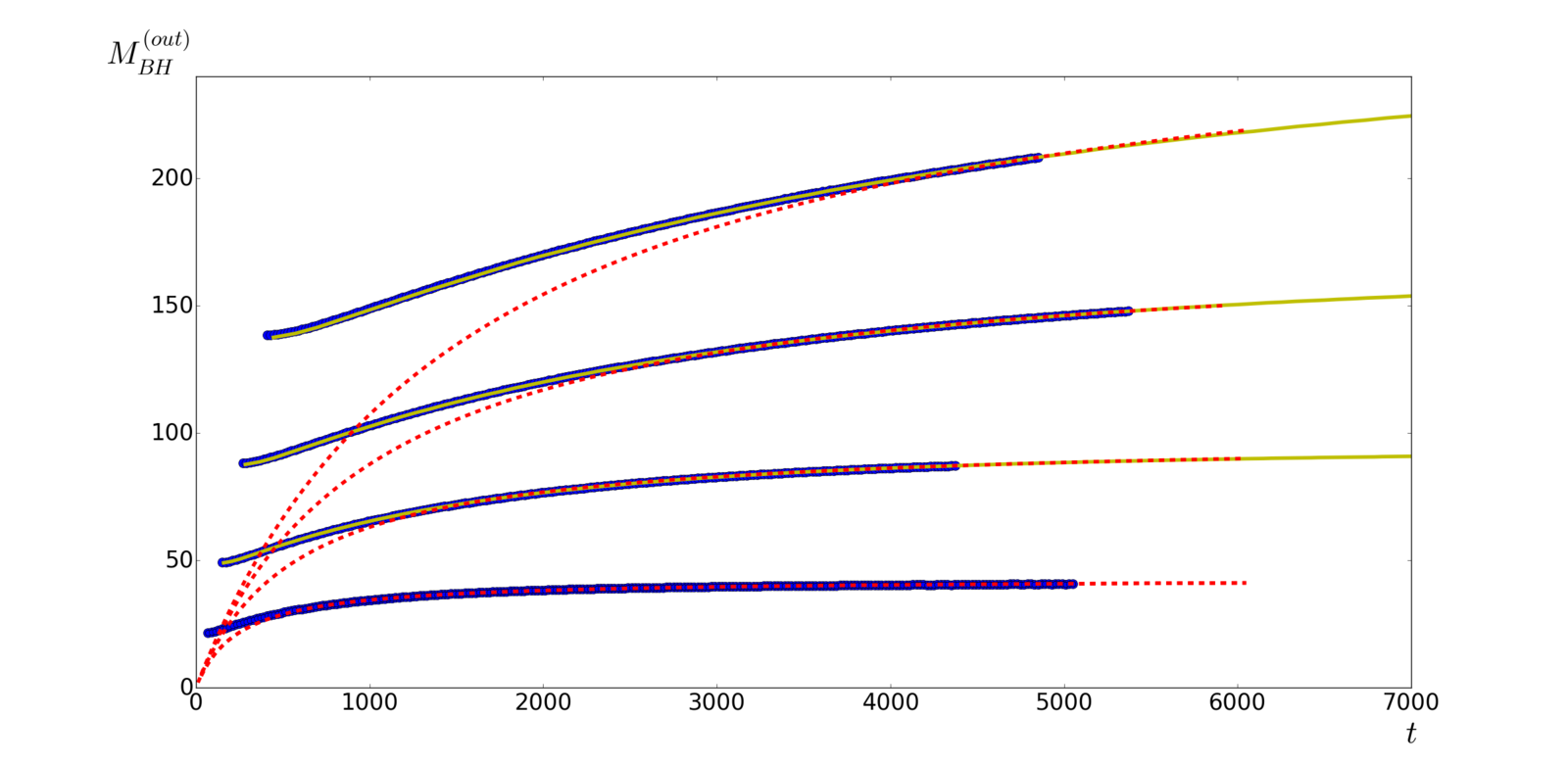
- Outer BH mass accretion
M_{BH2}^{(out)}(Kt)=KM_{BH1}^{(out)}(t)
Self-similar process
K\approx\frac{M_{BHi2}}{M_{BHi1}}\approx\left(\frac{r_{i2}}{r_{i1}}\right)^{2}
where
\frac{M_{BHf2}^{(out)}}{M_{BHf1}^{(out)}}\approx\left(\frac{r_{i2}}{r_{i1}}\right)^{2}
M_{BHf}^{(out)}\approx2M_{BHi}
We found that

Conclusions
-
Subcritical
Dust
\ M_{BHf} = M_H
M_{BHf} \sim \sigma R_H^2
Radiation
-
Supercritical
Dust
M^{(out)}_{BHf} \approx 2M^{(in)}_{BHf} \approx 5.6 M_H
Radiation
M^{(out)}_{BHf}, M^{(in)}_{BHf} = M_H
deck
By Heling Deng
deck
- 454



