Heling Deng
with Alex Vilenkin, Jaume Garriga and Masaki Yamada
- Background
- Simulations
- Observational constraints
- Analytic estimates
- Background
- Simulations
- Observational constraints
- Analytic estimates
LIGO BH
Primordial Black Hole (PBH)
Supermassive black holes
LIGO black holes
Dark matter
SMBH
...
...
Stellar BH
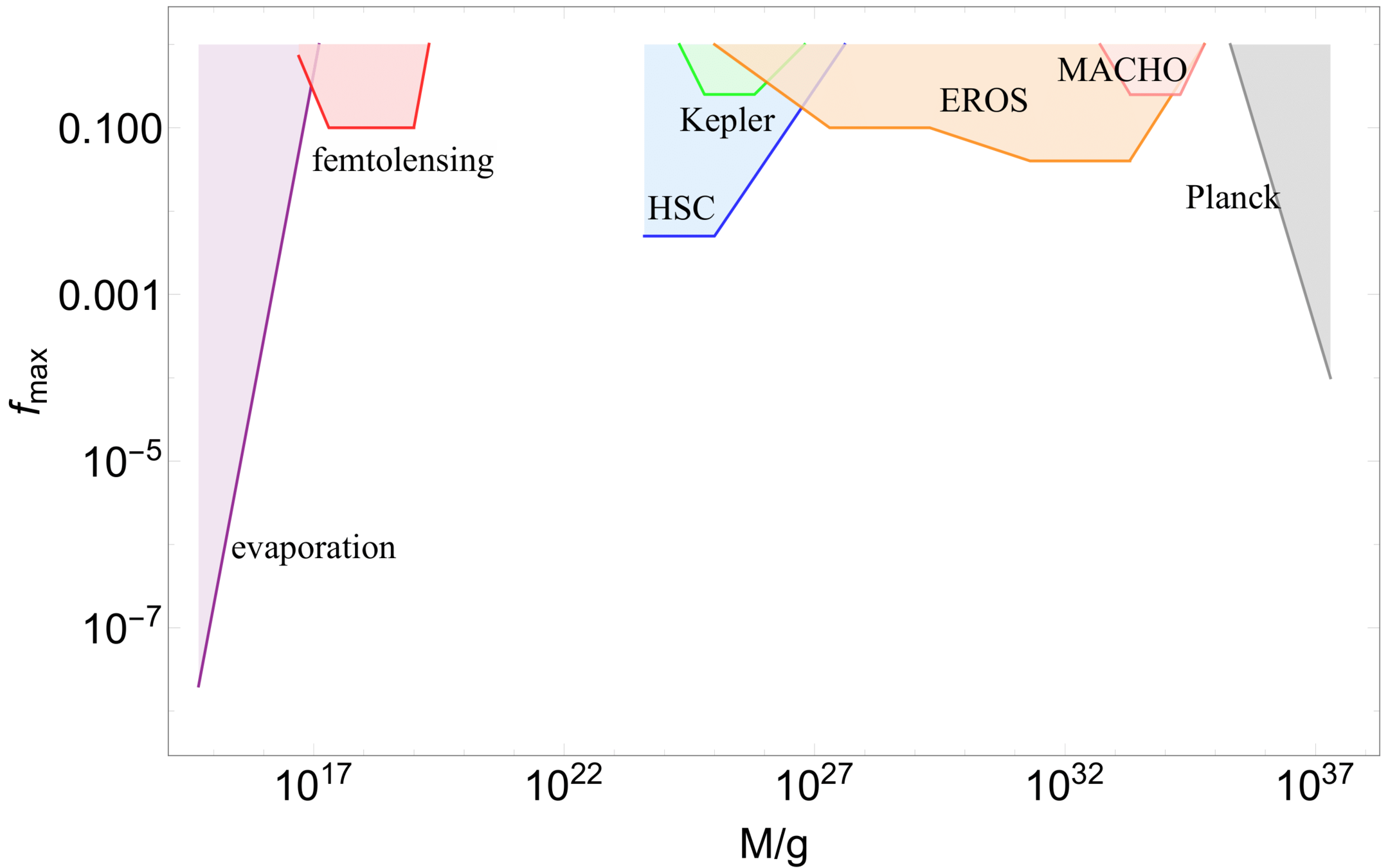
Observational constraints on PBH as DM
- Background
- Simulations
- Observational constraints
- Analytic estimates
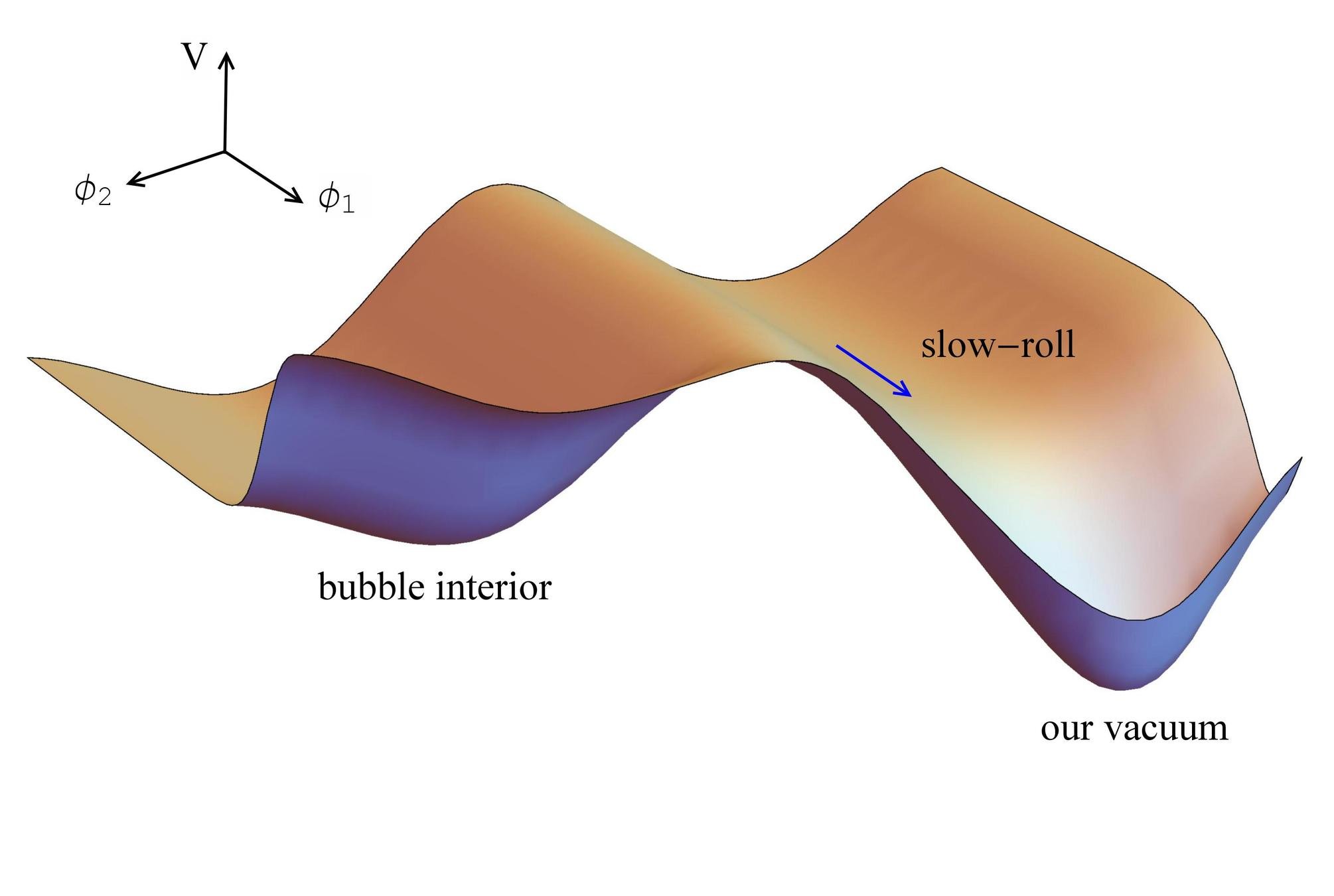



Inflation
Bubble interior
Inflation
Bubble interior
Radiation
Subcritical
BH
Subcritical
BH
Subcritical
Supercritical
BH
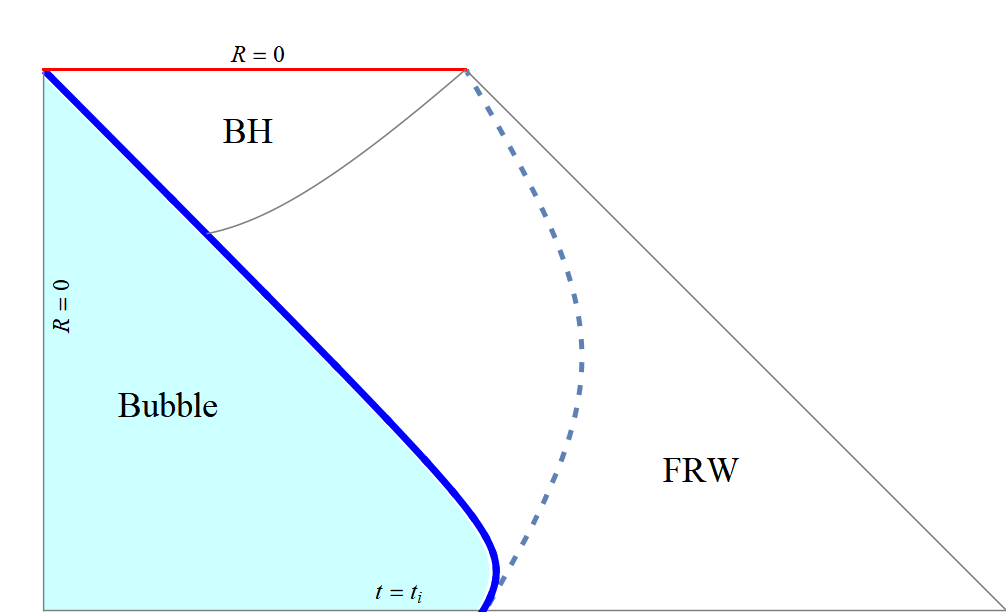
Spacetime and BH
Subcritical

Spacetime and BH
Subcritical
Spacetime and BH
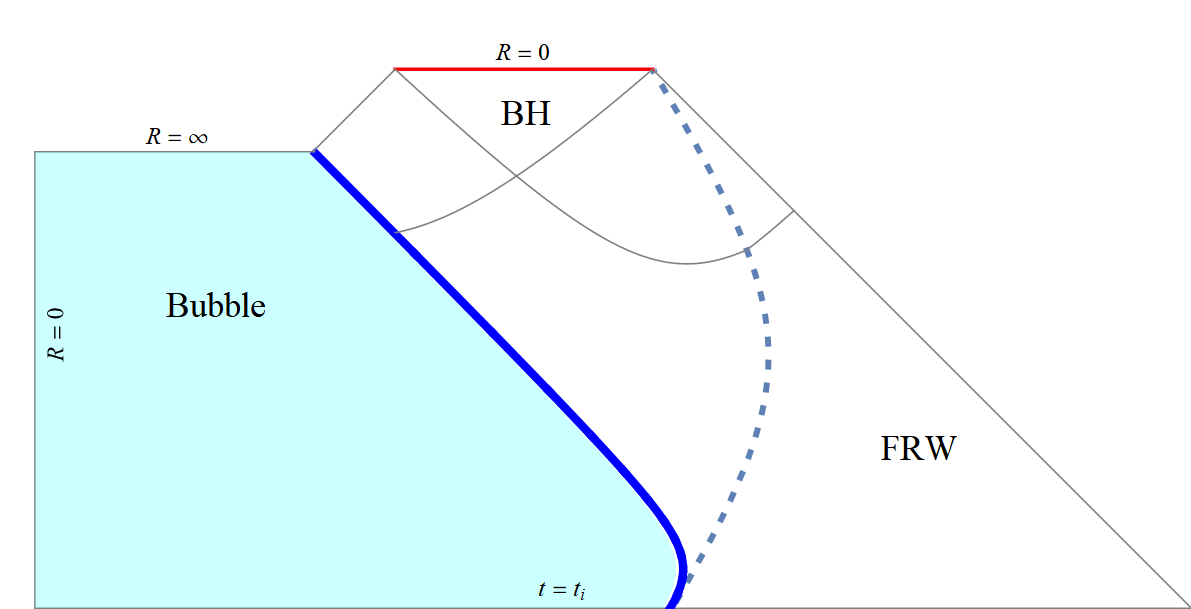
Supercritical
Spacetime and BH

Supercritical
Spacetime and BH

Supercritical
Spacetime and BH

Supercritical
Spacetime and BH

Supercritical
Spacetime and BH

Supercritical
Spacetime and BH

Supercritical
Spacetime and BH

Supercritical
Spacetime and BH

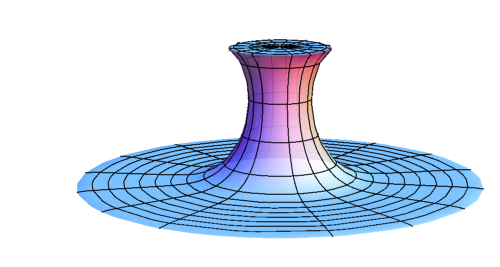
Supercritical

Spacetime and BH

upper bound:
Subcritical
Supercritical
- Background
- Simulations
- Observational constraints
- Analytic estimates
Metric
Fluid
Radiation
BH apparent horizon
Misner-Sharp mass
Early stage of evolution of \(\rho \)
Evolution of \(\rho \) after BH formation (subcritical)
Evolution of \(\rho \) at late time (subcritical)
Evolution of \(\rho \) after BH formation (supercritical)
Estimates
Sub:
Super:
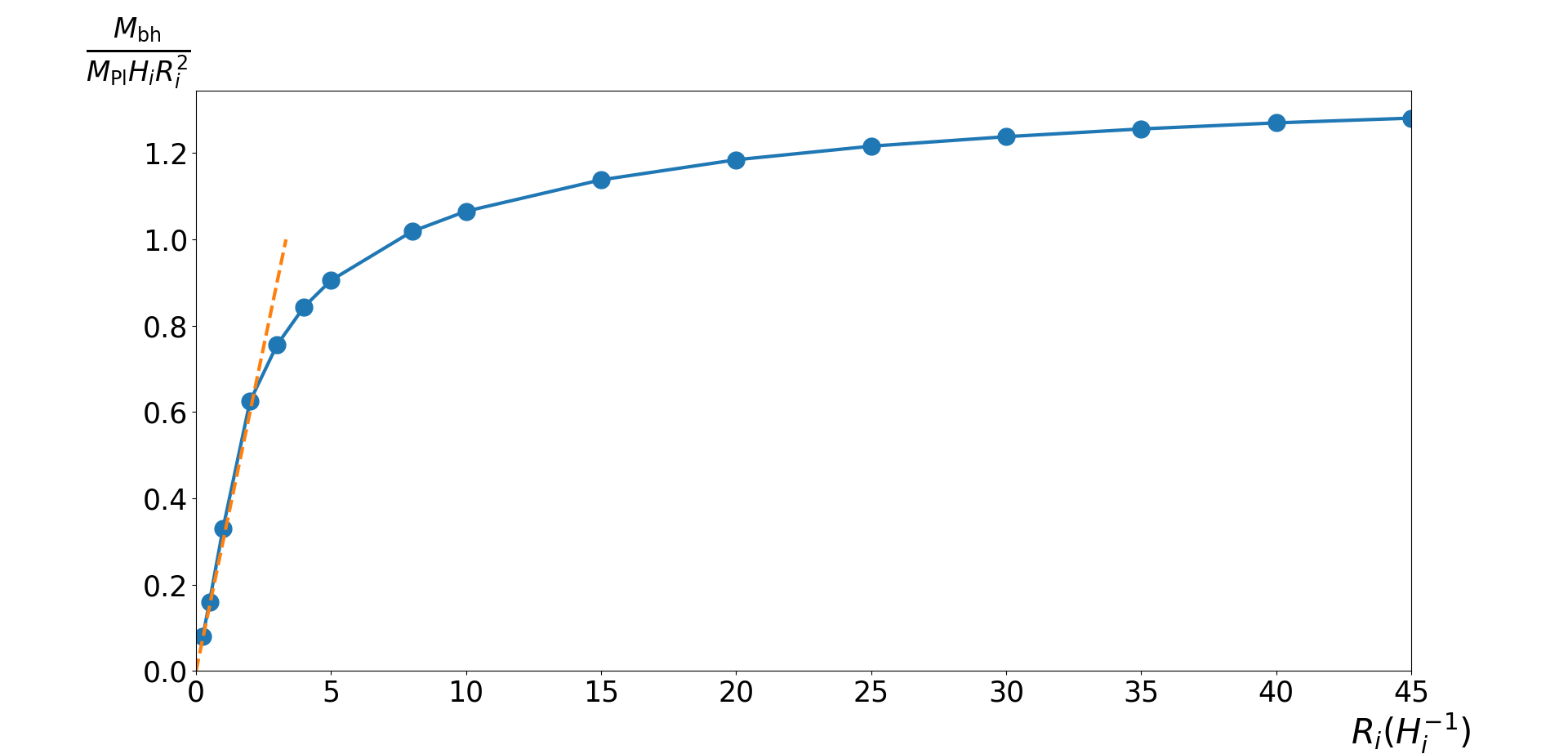
Simulations
BH mass
BH mass
where
- Background
- Simulations
- Observational constraints
- Analytic estimates
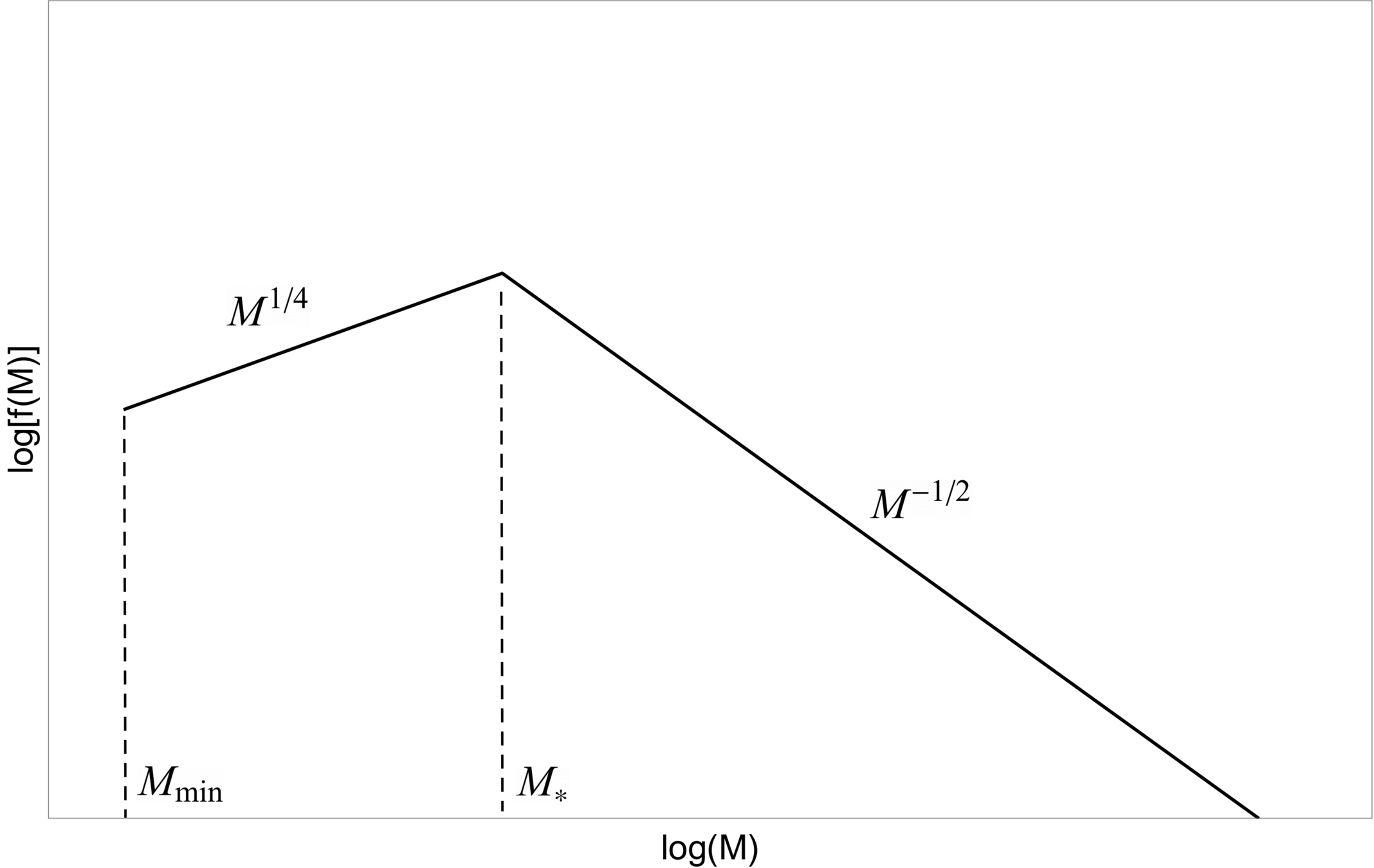
BH mass distribution
PBH mass function (fraction of DM in PBH with mass \(\sim M\))
Mass density after inflation (\(\sim M\))
Number density after inflation (\(\sim R_i\))
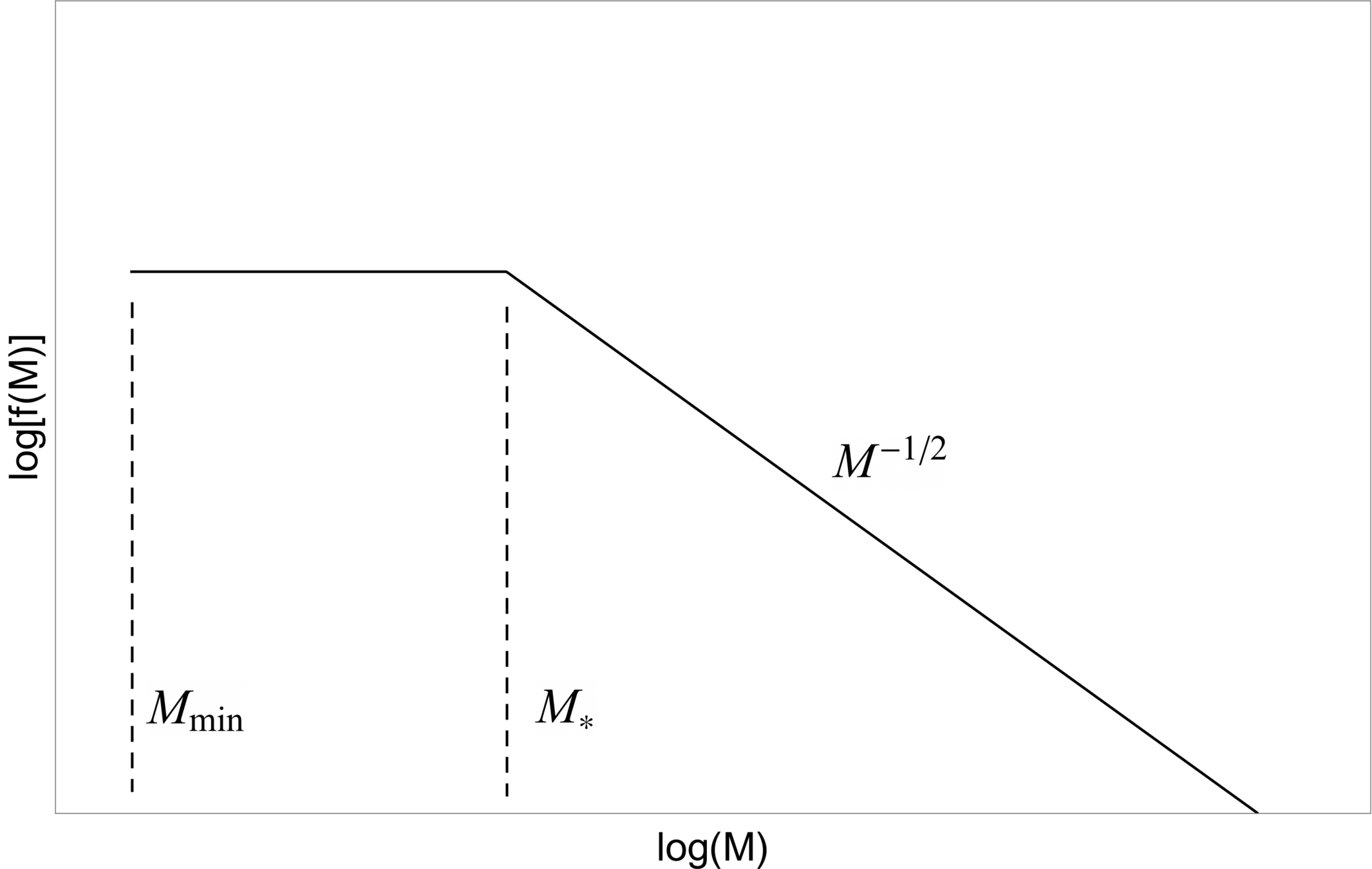
Lower cutoff
Bubble wall fluctuations
Small bubbles
BH mass distribution

Observational constraints on monochromatic PBH
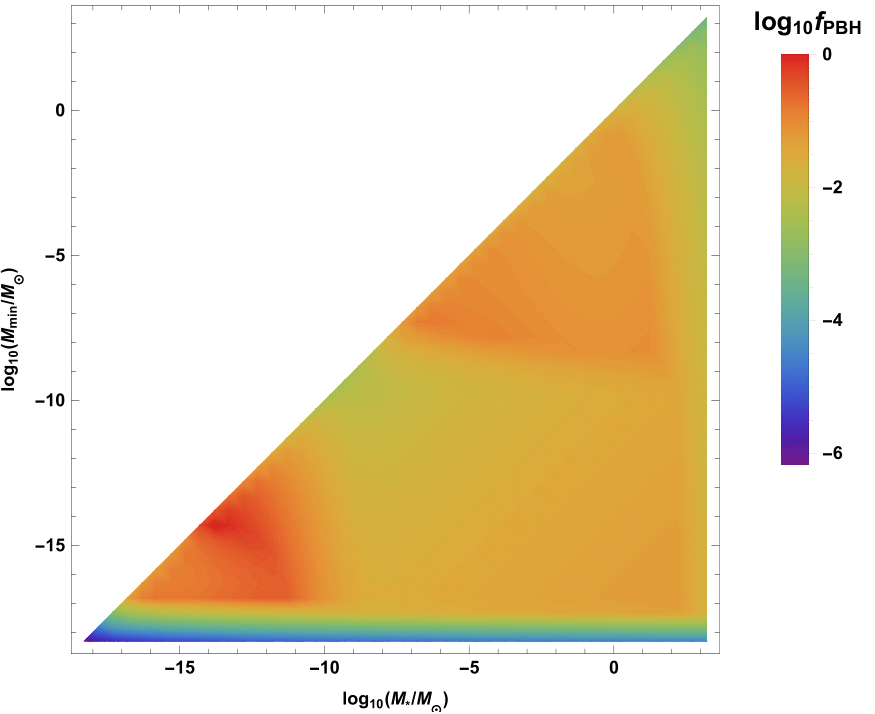
Observational constraints on our PBH
LIGO PBH?
\(f(M\sim 30\ M_\odot) \sim 10^{-3} \ \to \) merger rate for LIGO events
1603.08338 Misao Sasaki, Teruaki Suyama, Takahiro Tanaka, and Shuichiro Yokoyama (2016)
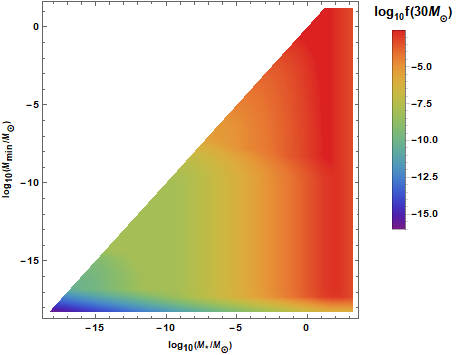
SMBH?
\(M \gtrsim 10^3\ M_\odot \ \to \) primordial seeds of SMBH
astro-ph/0406260 Norbert Duechting (2004)
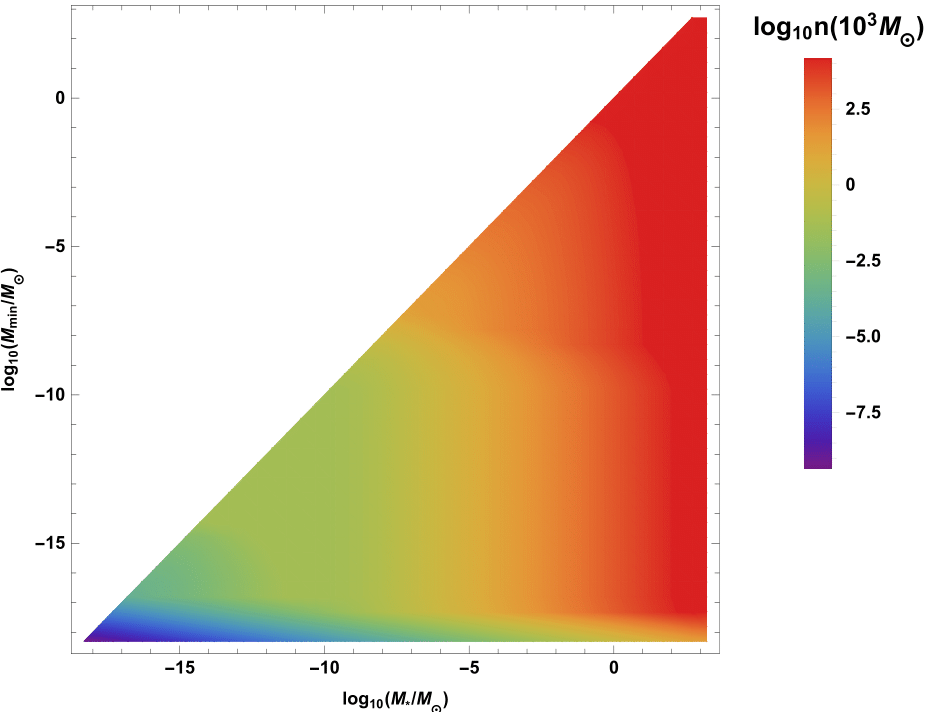
Galaxy number density:
All DM
SMBH
LIGO


CMB distortion?
CMB: black-body spectrum (no chemical potential)
\(\mu \)-era:
photon number changing processes are ineffective
Photon number not conserved
\(\mu \)-distortion: spectrum with chemical potential
Photon diffusion
Silk damping: wiping off inhomogeniety
CMB distortion?
BH
BH
BH
BH
BH
BH
Photon diffusion length at recombination
BH
BH
BH
BH
BH
BH
BH
BH
BH
BH
Photon diffusion length at recombination
BH
BH
BH
BH
BH
BH
BH
BH
Photon diffusion length at recombination
\(\bar \mu \) dominated by
Photon diffusion length at recombination
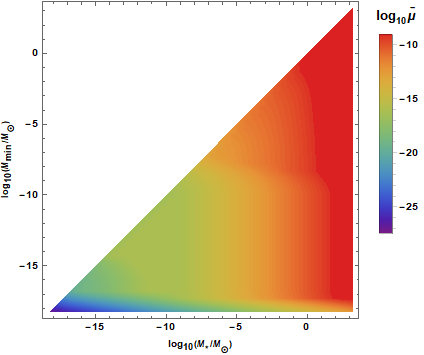
Observational constraints on \(\mu \)-distortion
Possible large BHs in some rare regions on LSS \(\to\) spiky \(\mu\)
Observations:
Observations:

Conclusions
- This model can be naturally implemented in landscape models of the kind suggested by string theory
- Depending on their sizes after inflation ends, bubbles can be classified into two categories: subcritical and supercritical, both leading to black hole formation
- It predicts distinctive PBH mass spectra, ranging over many orders of magnitude
- With some parameter choices, these PBH can account for SMBHs, for the black hole mergers observed by LIGO, and/or for the dark matter
- It predicts a spiky distribution of \(\mu \)-distortion in CMB
Bubble size distribution
Bubble radius during inflation
Number of bubbles
Number density during inflation
Number density after inflation
CMB distortion?
Photon diffusion
Silk damping: wiping off inhomogeniety
Damping scale:
\(\mu \)-era:
Recombination:
sound horizon (shell comoving radius)
(Silk patch)
- Background
- Spherical domain walls
- Conclusions
- Vacuum bubbles



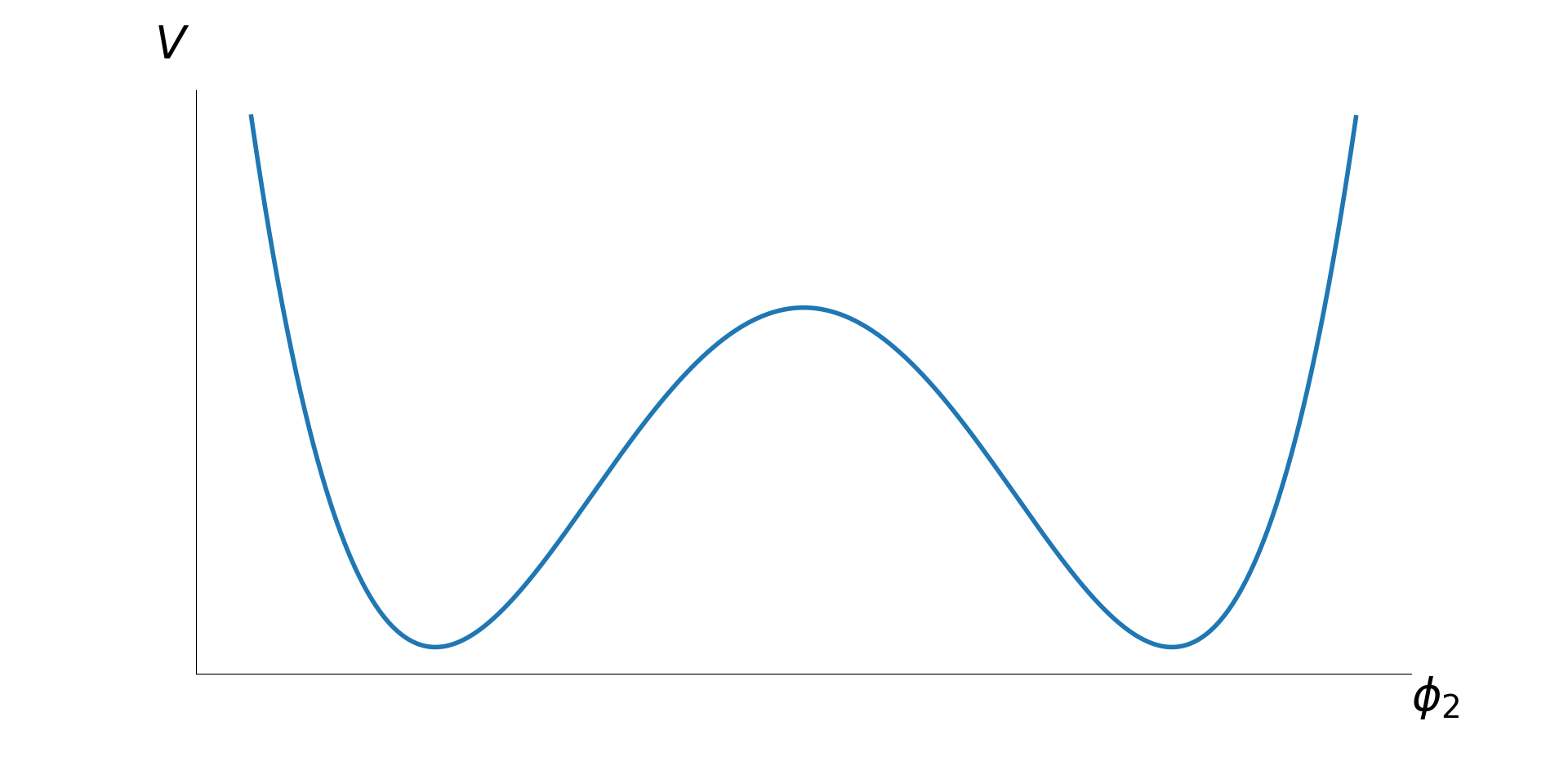
Inflation
Inflation
Radiation
BH mass distribution
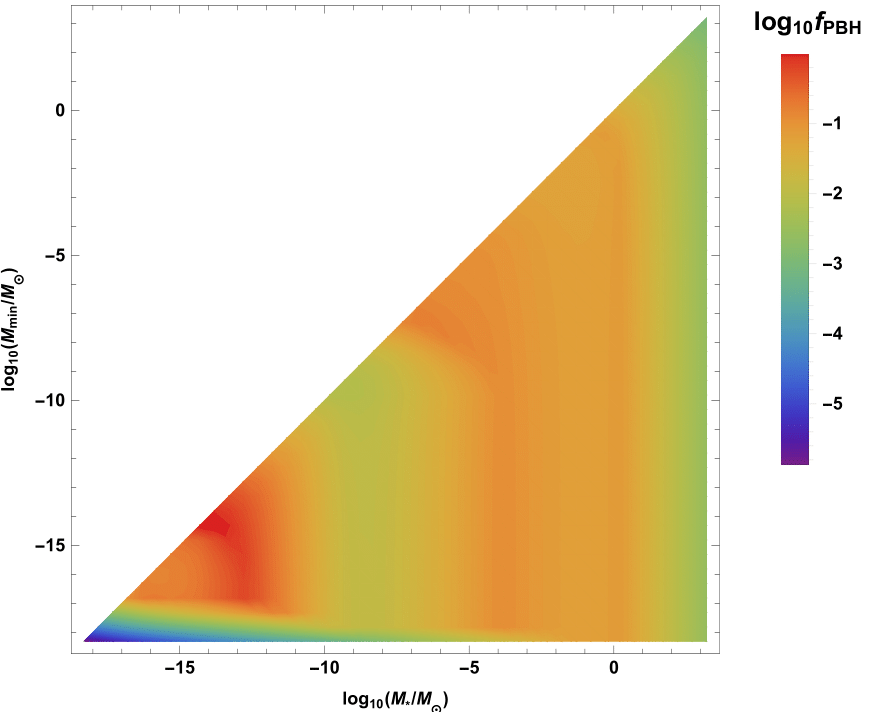
Observational constraints on our PBH
Repulsive planar wall
- Constant acceleration away from the wall
- Exponential expansion on the wall
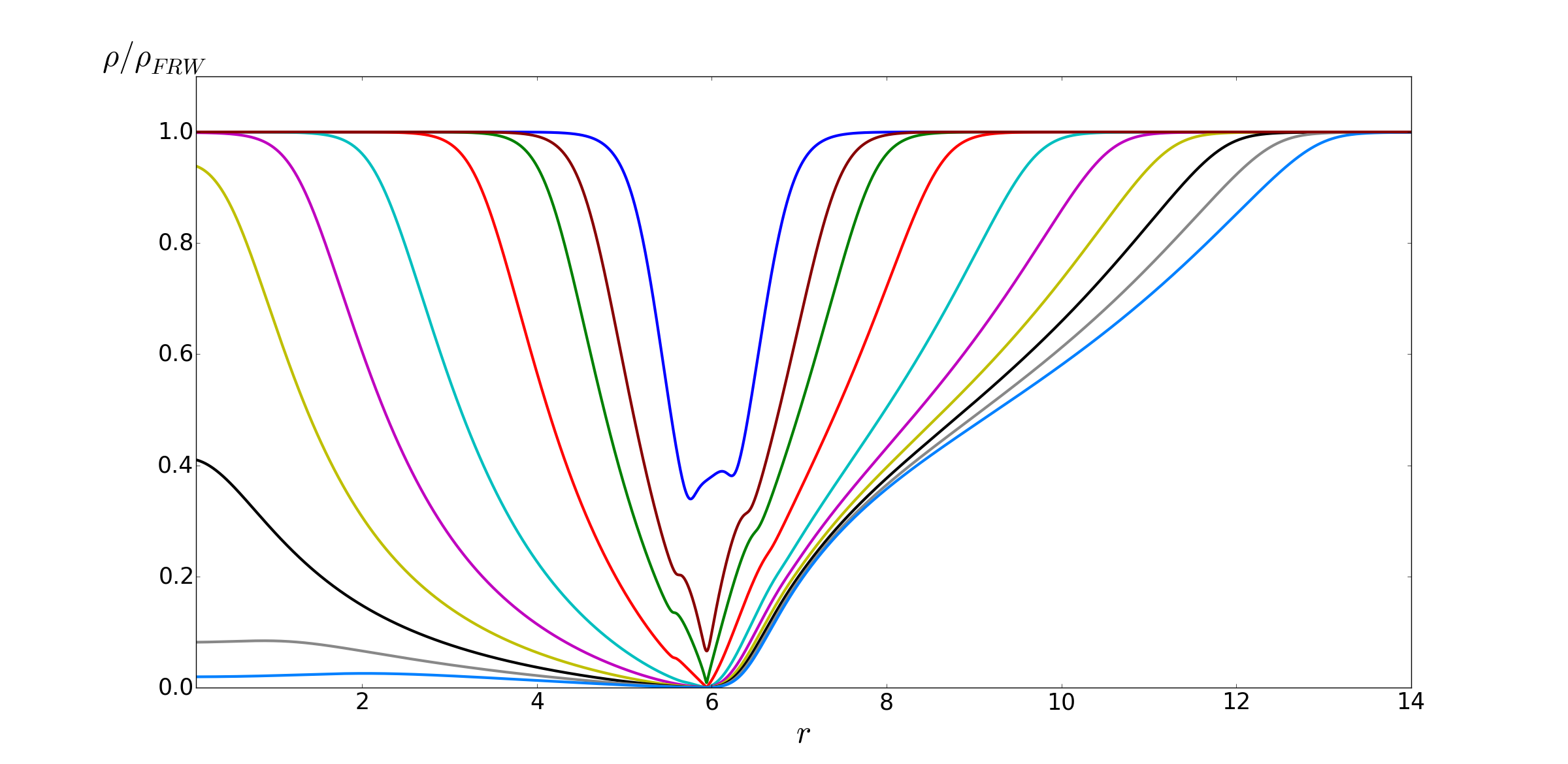
Evolution of \(\rho \)
Inflating wall
where
Hubble crossing
Gravity vs. Tension
Subcritical:
Supercritical:
where
Hubble crossing
Gravity vs. Tension
Subcritical:
Supercritical:
Subcritical
BH
Inflating wall
where
Hubble crossing
Gravity vs. Tension
Subcritical:
Supercritical:

Supercritical
Subcritical
BH
upper bound:
Inflating wall
BH mass
where
- results
- simulation setup
- observations
- dynamics & spacetime
Metric
Fluid
radiation
boundary condition
outer: FRW solutions
inner: junction conditions
initial condition
- results
- simulation setup
- observations
- dynamics & spacetime
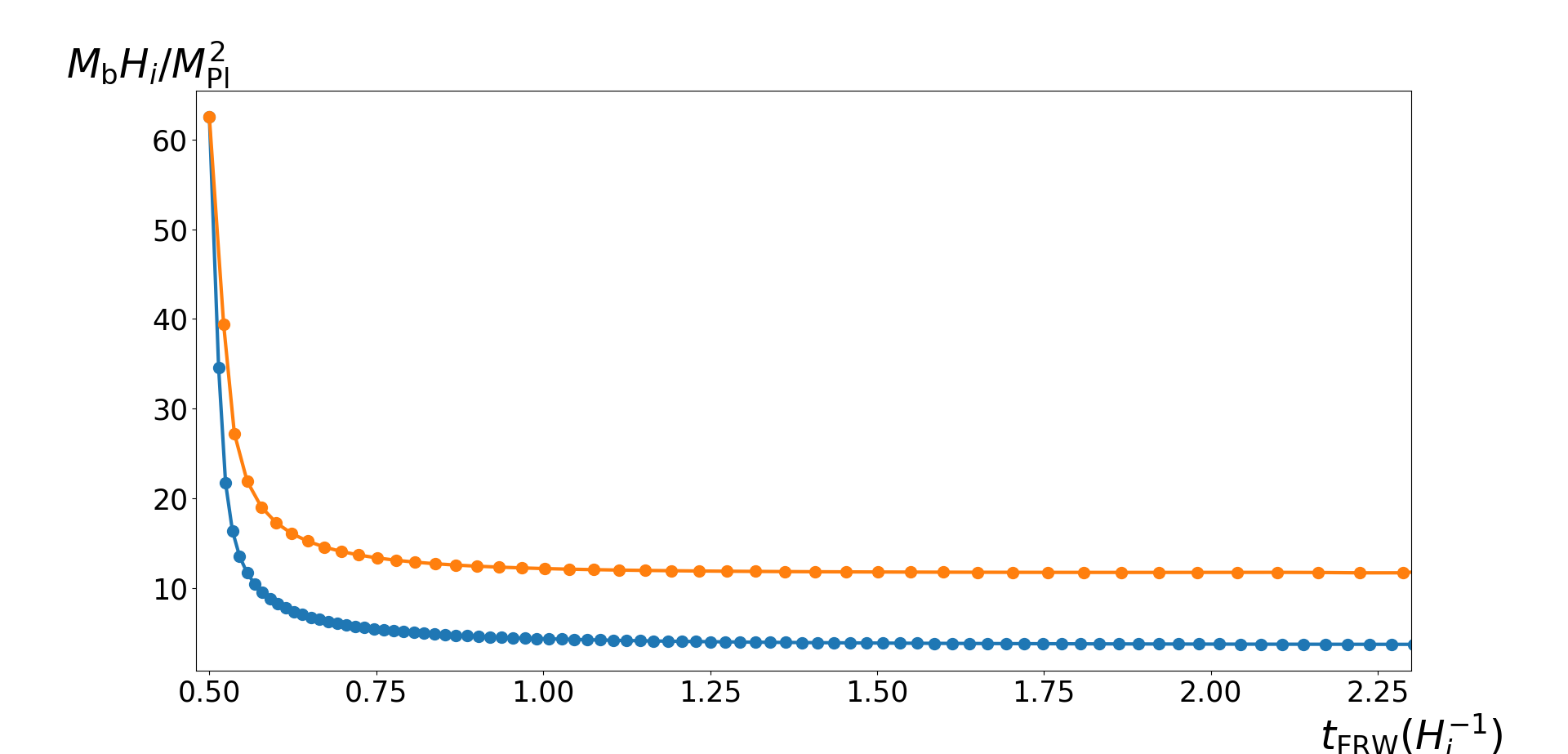
early stage of evolution of bubble mass
| parameters | |||
|---|---|---|---|
| 2 | 0.5 | 0.3 | |
| 3 | 1.7 | 1.0 | |
| 4 | 3.9 | 2.1 | |
| 5 | 7.9 | 3.7 | |
| 2 | 0.8 | 0.7 | |
| 1.8 | 0.8 | 0.9 | |
| 1 | 0.3 | 0.3 |
subcritical BH mass
Total fraction of CDM in PBH
Copy of PBHs from Bubbles
By Heling Deng
Copy of PBHs from Bubbles
- 448



