Profunctor Optics

Overview

Algebraic Data Types
Lens Library
Functors
Profunctor Optics

lens

type Iso' s a =
  forall p f. (Profunctor p, Functor f) => p a (f a) -> p s (f s)

type Lens' s a =
  forall f. (Functor f) => (a -> f a) -> s -> f s

type Prism' s a =
  forall p f. (Choice p, Applicative f) => p a (f a) -> p s (f s)

type Traversal' s a =
  forall f. (Applicative f) => (a -> f a) -> s -> f s

type Fold s a =
  forall p f. (Contravariant f, Applicative f) => a (f a) -> s -> f s

purescript-profunctor-lenses

type IsoP s a =
  forall p. (Profunctor p) => p a a -> p s s

type LensP s a =
  forall p. (Strong p) => p a a -> p s s

type PrismP s a =
  forall p. (Choice p) => p a a -> p s s

type TraversalP s a =
  forall p. (Wander p) => p a a -> p s s

type FoldP r s a =
  Forget r a a -> Forget r s s

Algebraic Data Types

to the code...

Sum Types

data IorB = I Int | B Bool

Sum Types

data IorB = I Int | B Bool
type IorB' = Either Int Bool

-- `IorB <~> Either Int Bool`

--           IorB -> IorB'
matchIorB :: IorB -> Either Int Bool
matchIorB (I n) = Left n
matchIorB (B b) = Right b

--            IorB'           -> IorB
injectIorB :: Either Int Bool -> IorB
injectIorB (Left n)  = (I n)
injectIorB (Right b) = (B b)

Are isomorphic to Either

Sum Types

data IorB = I Int | B Bool

-- Sum examples

five :: IorB
five = I 5

truuu :: IorB
truuu = B True

Values of the Day:

Product Types

data Person = P
  { _pName :: String
  , _pAge  :: Int
  }

data AlsoPerson = AP String Int

Product Types

-- | `P String Int <~> (String, Int)`

type Person = (String,Int)

-- |      Person -> Person'
splitP :: Person -> (String, Int)
splitP (P name age) = (name, age)

-- |        Person'       -> Person
unsplitP :: (String, Int) -> Person
unsplitP (name, age) = P name age

Product Types

data Person = P
  { _pName :: String
  , _pAge  :: Int
  }

-- Values

john :: Person
john = P "John" 889

sue :: Person
sue = P "Sue" 407

Values of the Day:

Lens Library

Lenses
Prisms
Isos
Traversals
Folds

Lens Library

Challenge:

Given a list of homeowners, modify each homeowner's address by capitalizing each address' street name:

Lens Library

// Java

for (Homeowner owner : ArrayList<HomeOwner>) {
    person.address.street.name.toUpper()
}

-- Haskell

fmap updateHomeOwner homeowners
  where updateHomeOwner (HomeOwner name age address)
          = HomeOwner name age (updateAddress address)
        updateAddress (Address (Street no name) state zip))
          = Address (Street no (toUpper name)) state zip

Lens Library

-- Haskell

over (traverse.address.street.name) toUpper homeowners

// Java

for (Homeowner owner : ArrayList<HomeOwner>) {
    person.address.street.name.toUpper()
}

Lens Library

λ> view pName john
"John"
λ> view pName sue
"Sue"
λ> view pAge john
889
λ> view pAge sue
407
λ> set pAge 10 sue
P {_pName = "Sue", _pAge = 10}
λ> set pName "Sue" john
P {_pName = "Sue", _pAge = 889}
λ> over pAge (+111) john
P {_pName = "Sue", _pAge = 889}

Person lenses pName and pAge

john :: Person
john = P "John" 889

sue :: Person
sue = P "Sue" 407

pName :: Lens' Person String
pAge :: Lens' Person Int

Lens Library

λ> preview _I five
Just 5
λ> preview _B five
Nothing
λ> preview _I truuu
Nothing
λ> preview _B truuu
Just True
λ> review _B True
B True
λ> review _I 5
I 5
λ> over _I (+95) five
I 100

IorB prisms _I and _B

five :: IorB
five = I 5

truuu :: IorB
truuu = B True

_I :: Prism' IorB Int
_B :: Prism' IorB Bool

Functors

Functor

(Covariant)

class Functor f where
  fmap :: (a -> b) -> f a -> f b

a -> b

Functor

class Functor f where
  fmap :: (a -> b) -> f a -> f b

-- | `[x] = [] x` where f=`[]` and a=`x`
λ> fmap (+10) [1,2,3,4]
[11,12,13,14]


-- | `(x,y) = (,) x y` where f=`(x,)` and a=`y`
λ> fmap (+10) (1,2)
(1,12)

-- | `data Either x y = Left x | Right y` where
-- | f=`Either x` and a=`y`
λ> fmap (+10) (Left 1)
Left 1
λ> fmap (+10) (Right 2)
Right 12

Bifunctor

class Bifunctor p where
  bimap :: (a -> b) -> (c -> d) -> p a c -> p b d

a -> b

c -> d

-- | `(x,y) = (,) x y` where f=`(,)` and
-- | a=`x` and b=`y`
λ> bimap (+10) (+50) (1,1)
(11,51)

-- | `data Either x y = Left x | Right y` where
-- | f=`Either` a=`x` and b=`y`
λ> bimap (+10) (+50) (Left 1)
Left 11
λ> bimap (+10) (+50) (Right 1)
Right 51

Bifunctor

class Bifunctor p where
  bimap :: (a -> b) -> (c -> d) -> p a c -> p b d

Contravariant Functor

class Contravariant f where
  contramap :: (a -> b) -> f b -> f a

a -> b

Contravariant Functor

class Contravariant f where
  contramap :: (a -> b) -> f b -> f a

a -> b

Profunctor

class Profunctor p where
  dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
  lmap :: (a -> b) -> p b c -> p a c
  rmap :: (b -> c) -> p a b -> p a c

a -> b

c -> d

Profunctor

class Profunctor p where
  dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
  lmap :: (a -> b) -> p b c -> p a c
  rmap :: (b -> c) -> p a b -> p a c

a -> b

c -> d

Profunctor takes a "pre-computation", a "post-computation", and an intermediate relationship between
between things

Profunctor

class Profunctor p where
  dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
  lmap :: (a -> b) -> p b c -> p a c
  rmap :: (b -> c) -> p a b -> p a c

a -> b

c -> d

Strong Profunctor

-- | The "operate on a part of a whole" typeclass
class Profunctor p => Strong p where
    first' :: p a b -> p (a, q) (b, q)

Think of the following:

• p a b as a relationship on a part
• p (a,q) (b,q) as a relationship on the whole

Strong Profunctor

-- | The "operate on a part of a whole" typeclass
class Profunctor p => Strong p where
    first' :: p a b -> p (a, q) (b, q)

(a,q)

(b,q)

Choice Profunctor

-- | The "operate on a branch of a
-- | possibility" typeclass
class Profunctor p => Choice p where
    left' :: p a b  -> p (Either a q) (Either b q)

Think of the following:

• p a b as a relationship on a branch
• p (Either a q) (Either b q) as a relationship on all possibilities

Choice Profunctor

-- | The "operate on a branch of a
-- | possibility" typeclass
class Profunctor p => Choice p where
    left' :: p a b  -> p (Either a q) (Either b q)

Either a q

Either b q

to the code...

Profunctor Optics

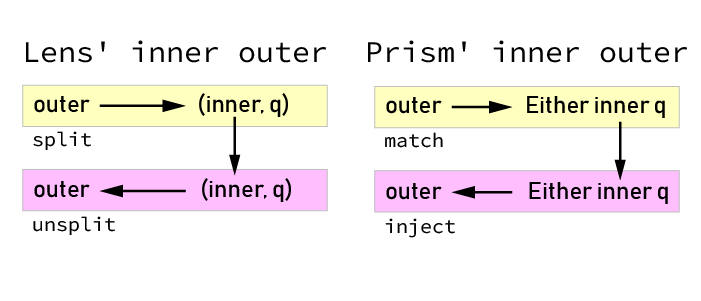
Simple Optics

Lens' inner outer and Prism' inner outer isomorphisms

https://blog.jle.im/entry/lenses-products-prisms-sums.html

Profunctor Optics

Lens Families

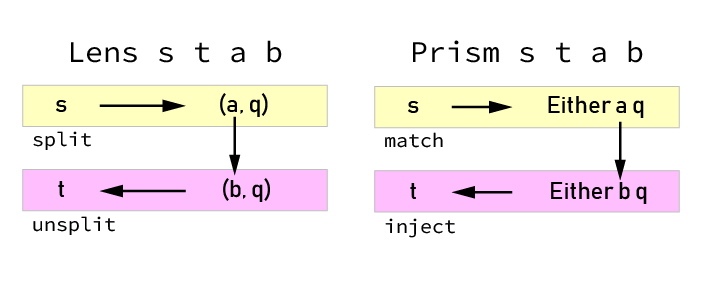
Lens s t a b and Prism s t a b isomorphisms, as a lens family

https://blog.jle.im/entry/lenses-products-prisms-sums.html

purescript-profunctor-lenses

type IsoP s a =
  forall p. (Profunctor p) => p a a -> p s s

type LensP s a =
  forall p. (Strong p) => p a a -> p s s

type PrismP s a =
  forall p. (Choice p) => p a a -> p s s

-- class (Strong p, Choice p) => Wander p where..
type TraversalP s a =
  forall p. (Wander p) => p a a -> p s s

type FoldP r s a =
  Forget r a a -> Forget r s s

Profunctor Optics

type Optic c s t a b = forall p. c p => p a b -> p s t

type Optic c s t a b = forall p. c p => p a b -> p s t

C =

Strong

Traversing1

Choice

Bicontravariant

Bifunctor

Mapping

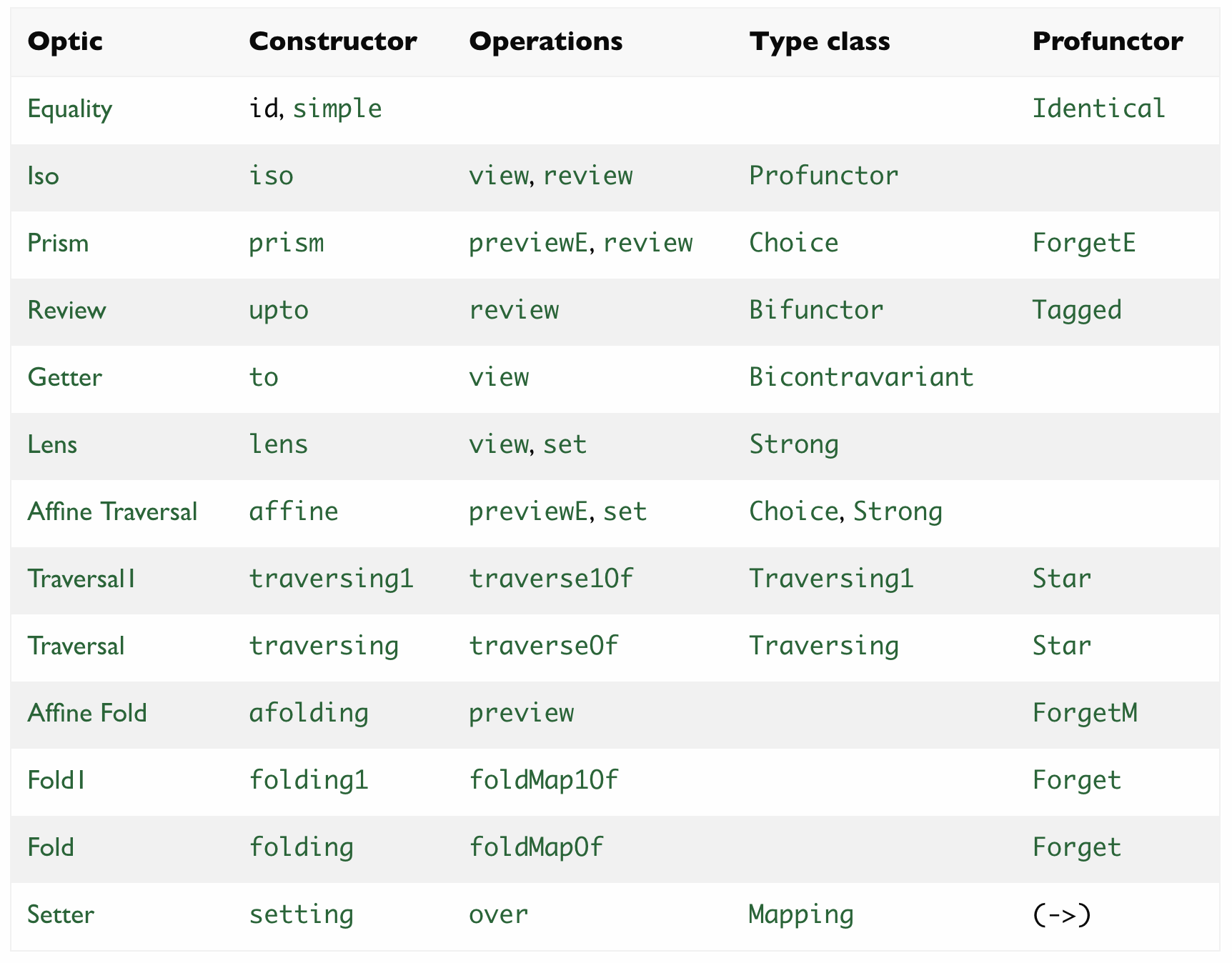
http://oleg.fi/gists/posts/2017-04-18-glassery.html

Profunctor Optics

By Heneli Kailahi

Profunctor Optics

Overview

lens

purescript-profunctor-lenses

Algebraic Data Types

Sum Types

Sum Types

Sum Types

Product Types

Product Types

Product Types

Lens Library

Lens Library

Lens Library

Lens Library

Lens Library

Lens Library

Lens Library

Functors

Functor

Functor

Bifunctor

Bifunctor

Contravariant Functor

Contravariant Functor

Profunctor

Profunctor

Profunctor

Strong Profunctor

Strong Profunctor

Choice Profunctor

Choice Profunctor

Profunctor Optics

Profunctor Optics

Profunctor Optics

purescript-profunctor-lenses

Profunctor Optics

Profunctor Optics

More from Heneli Kailahi