Type Level Programming
In Haskell
Plan
- What is Type Level Programming?
- Syntax Primer
- Algebra of Types
- Kind System
- GADTs
- Type Families
- Rank Polymorphism
-
Type Variables
- Scope and Application
- First Class Families
- Defuntionalization
What am I skipping?
- Existentials
- Eliminators
- ST Trick
- Rigid Skolems
- Servant
- What and How?
- Why?
- Expression Problem
- Data Families
- vs GADTs
- Role System
- Scalar operations on higher ranked data
Typical Haskell
-
Terms
- the values you can manipulate
- exist at runtime
- inhabit some type
- Types
- proofs to the compiler (and ourselves) that the programs we’re trying to write make some amount of sense (aka typechecks)
isOdd :: Int -> Bool
isOdd n = FalseType-Level Haskell
-
Types
- the values you can manipulate
- exist at compile time
- inhabit some kind
- Kinds
- proofs to the compiler (and ourselves) that the programs we’re trying to write make some amount of sense (aka kindchecks)
type family IsOdd (n :: GHC.TypeLits.Nat) :: Bool where
IsOdd n = 'FalseKinds
- Kind system
- “the type system for types”
- Kinds
- “the types of types”
{-# LANGUAGE UndecidableInstances, KitchenSink #-}
import Fcf -- (=<<), Eval, Not, TyEq
import GHC.TypeLits -- Mod, Nat(0..)
------------------------------------
-- Term Level
isOdd :: Int -> Bool
isOdd n = (mod n 2) /= 0
-- λ> isOdd 11
-- True
------------------------------------
-- Type Level
type family IsOdd (n :: Nat) :: Bool where
IsOdd n = Eval (Not =<< (TyEq (Mod n 2) (0)))
-- λ> :kind! IsOdd 10
-- IsOdd 11 :: Bool
-- = 'True
Type Level Programming
Constructing programs which execute at compile time taking types as input and return as output both new types and runtime functionality

Beware!
Haskell Primer
Data Types
data Bool = True | False
data [a] = [] | a : [a]filter :: (a -> Bool) -> [a] -> [a]
filter pred [] = []
filter pred (x:xs) =
case pred x of
False -> x : filter pred xs
True -> filter pred xs
Functions
Data Types
data Bool = True | False
data [a] = [] | a : [a]
data Three a b c = Three a b cfalse = False :: Bool
fives = [5,5,5,5,5] :: [Int]
three = Three 10 (-10) 9001 :: Three Int Int Int- Declare new data types with data
Data Types
data Bool = True | False
data [a] = [] | a : [a]
data Three a b c = Three a b cfalse = False :: Bool
fives = [5,5,5,5,5] :: [Int]
three = Three 10 (-10) 9001 :: Three Int Int IntType Constructor
Data Constructor
filter :: (a -> Bool) -> [a] -> [a]
filter pred [] = []
filter pred (x:xs) =
case pred x of
False -> x : filter pred xs
True -> filter pred xs
Functions
filter :: (a -> Bool) -> [a] -> [a]
filter pred [] = []
filter pred (x:xs) =
case pred x of
False -> x : filter pred xs
True -> filter pred xs
Functions
Type Signature
filter :: (a -> Bool) -> [a] -> [a]
filter pred [] = []
filter pred (x:xs) =
case pred x of
False -> x : filter pred xs
True -> filter pred xs
Functions
Parametric Polymorphism
filter :: (a -> Bool) -> [a] -> [a]
filter pred [] = []
filter pred (x:xs) =
case pred x of
False -> x : filter pred xs
True -> filter pred xs
Functions
Higher Order Function
filter :: (a -> Bool) -> [a] -> [a]
filter pred [] = []
filter pred (x:xs) =
case pred x of
False -> x : filter pred xs
True -> filter pred xs
Functions
Patterns
class Num a where
(+) :: a -> a -> a
(-) :: a -> a -> a
(*) :: a -> a -> aClasses and Instances
instance Num Int where
(+) :: Int -> Int -> Int
a + b = plusInt a b
(-) :: Int -> Int -> Int
a - b = minusInt a b
(*) :: Int -> Int -> Int
a * b = timesInt a bsquare :: Num a => a -> a
square x = x * x
class Num a where
(+) :: a -> a -> a
(-) :: a -> a -> a
(*) :: a -> a -> aClasses and Instances
instance Num Int where
(+) :: Int -> Int -> Int
a + b = plusInt a b
(-) :: Int -> Int -> Int
a - b = minusInt a b
(*) :: Int -> Int -> Int
a * b = timesInt a bsquare :: Num a => a -> a
square x = x * x
Context / Constraint
Ad Hoc Polymorphism
Algebra of Types
Algebra behind ADTs
- Cardinality — the number of inhabitants in a type (ignoring bottoms)
data Void
data () = ()
data Bool = False | True
data Alphabet a c = Alphabet a Bool c
data Maybe a = Nothing | Just aAlgebra behind ADTs
-- 0
data Void
-- 1
data () = ()
-- 1 + 1 = 2
data Bool = False | True
-- |a| * 2 * |c|
data Alpha a c = Alphabet a Bool c
-- 1 + |a|
data Maybe a = Nothing | Just a|Void| = 0
|()| = 1
|Bool|= 2
|Alpha Bool Bool| = 8
|Maybe ()| = 2
Isomorphism
- Any two types that have the same cardinality will always be isomorphic to one another.
- An isomorphism between types s and t is defined as a pair of functions to and from such that composing either after the other gets you back where you started.

s t
to :: s -> t
to = _
from :: t -> s
from = _
to . from = id
from . to = idIsomorphism

s t
data S = S deriving Show
data T = T deriving Showλ> (toT . fromT) T
T
λ> (fromT . toT) S
StoT :: S -> T
toT S = T
fromT :: T -> S
fromT T = SIsomorphism

s t
data S = S deriving Show
data T = T deriving Showλ> (fromT . toT) S
S
λ> (toT . fromT) T
TtoT :: S -> T
toT S = T
fromT :: T -> S
fromT T = StoS :: T -> S
toS T = S
fromS :: S -> T
fromS S = Tλ> (fromS . toS) T
T
λ> (toS . fromS) S
SIdentity
-
() as multiplicative identity
- |()| = 1
- a * 1 = a
prodUnitTo :: a -> (a, ())
prodUnitTo a = (a, ())
prodUnitFrom :: (a, ()) -> a
prodUnitFrom (a, ()) = a-
Void as additive identity
- |Void| = 0
- a + 0 = a
sumUnitTo :: Either a Void -> a
sumUnitTo (Left a) = a
sumUnitTo (Right v) = absurd v
sumUnitFrom :: a -> Either a Void
sumUnitFrom = LeftCardinality of (->)
- Function types correspond to exponentiation
|a -> b| = |b| × |b| × · · · × |b| = |b|^|a|
Basically states that for every value in a, there is a mapping to any value in b
Cardinality of (->)
id :: Bool -> Bool
id b = b
not :: Bool -> Bool
not = \case
False -> True
True -> FalseconstTrue :: Bool -> Bool
constTrue = const True
constFalse :: Bool -> Bool
constFalse = const False|Bool -> Bool| = |Bool| * |Bool| = |2| ^ |2| = 4
- Function types correspond to exponentiation
Curry-Howard Isomorphism
|
Algebra |
Logic |
Types |
|
a + b |
a ∨ b |
Either a b |
|
a × b |
a ∧ b |
(a, b) |
|
b ^ a |
a ⇒ b |
a -> b |
|
a = b |
a ⇐⇒ b |
isomorphism |
|
0 |
⊥ |
Void |
|
1 |
⊤ |
() |
- Every statement in logic is equivalent to some computer program, and vice versa
Insights from Curry-Howard Isomorphism
- Consider a^1 = a
-
() -> a is isomorphic to a
- Means that there is no distinction between having a value and having a (pure) program that computes that value
-
() -> a is isomorphic to a
Canonical Representations
- A direct corollary that any two types with the same cardinality are isomorphic, is that there are multiple ways to represent any given type.
- This canonical representation is known as a sum of products, and refers to any type t of the form
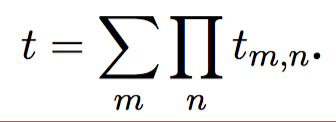
Kind System
{#- LANGUAGE PolyKinds -#}
{#- LANGUAGE KindSignatures -#}
{#- LANGUAGE DataKinds -#}Kinds
- Kind system
- “the type system for types”
- Kinds
- “the types of types”
Constraint Kinds
- Constraint is the kind of any fully saturated typeclass
{#- LANGUAGE ConstraintKinds -#}show :: Show a => a -> String- Show has kind Type -> Constraint
- Show Int has kind Constraint
- ConstraintKinds lets you to declare a tuple of constraints as a type synonym
type ReadShow a = (Read a, Show a)PolyKinds
- Introduce a kind k which can be higher-kinded
-
Proxy is poly-kinded, so Proxy anything will have kind Type
- Proxy Char where k is Type.
- Proxy (,) where k is Type -> Type
- Proxy Show where k is Type -> Constraint
- Proxy Monad where k is (Type -> Type) -> Constraint
{#- LANGUAGE PolyKinds -#}DataKinds
- Datatype Promotion
- The “promotion” of fully applied type constructors to kinds, and the promotion of certain data constructors to types
{#- LANGUAGE DataKinds -#}data Bool = False | True
-- Produces kind `Bool` and types `'True` and `'False`
-- λ> :k 'True
-- 'True :: Bool
-- λ> :k 'False
-- 'False :: BoolGADTs
{#- LANGUAGE GADTs -#}Type Equality
- Type Equality
- Constraint that two types are equal
- Form an equivalence relation
- Reflexivity - a type is equal to itself a ~ a
- Symmetry - a ~ b iff b ~ a
- Transitivity - if a ~ b and b ~ c, then a ~ c
- five and five_ are equivalent
five :: Int
five = 5
five_ :: (a ∼ Int) => a
five_ = 5{#- LANGUAGE GADTs -#}GADTS
- Generalized Algebraic Data Types
- Allow explicit type signatures to be written for data constructors
data Maybe a where
Nothing :: Maybe a
Just :: a -> Maybe a
just5 = Just 5data HList (xs :: [*]) where
HNil :: HList '[]
(:#) :: a -> HList as -> HList (a ': as)
infixr 5 :#
things :: HList '[Bool, Int, Int]
things = True :# 0 :# 10 :# HNilGADTS
data HList (xs :: [*]) where
HNil :: HList '[]
(:#) :: a -> HList as -> HList (a ': as)
infixr 5 :#
things :: HList '[Bool, Int, Int]
things = True :# 0 :# 10 :# HNil
instance Show (HList '[]) where
show HNil = "HNil"
instance (Show t, Show (HList ts))
=> Show (HList (t ': ts)) where
show (a :# as) = show a <> " :' " <> show as
-- λ> show things
-- "True :' 0 :' 10 :' HNil"- Common Pattern - Inductive definitions
GADTS
- Type Safe Syntax Tree
{#- LANGUAGE GADTs -#}data Expr a where
LitInt :: Int -> Expr Int
LitBool :: Bool -> Expr Bool
Add :: Expr Int -> Expr Int -> Expr Int
Not :: Expr Bool -> Expr Bool
If :: Expr Bool -> Expr a -> Expr a -> Expr a
evalExpr :: Expr a -> a
evalExpr (LitInt i) = i
evalExpr (LitBool b) = b
evalExpr (Add x y) = evalExpr x + evalExpr y
evalExpr (Not x) = not $ evalExpr x
evalExpr (If b x y) =
if evalExpr b then evalExpr x else evalExpr y
-- λ> evalExpr $ If (LitBool False)
-- (LitInt 1) (Add (LitInt 5) (LitInt 1))
-- 6
-- λ> evalExpr . Not $ LitBool True
-- FalseGADTS
- GADTs are just syntactic sugar over type equalities
{#- LANGUAGE GADTs -#}data Expr a where
LitInt :: Int -> Expr Int
LitBool :: Bool -> Expr Bool
Add :: Expr Int -> Expr Int -> Expr Int
Not :: Expr Bool -> Expr Bool
If :: Expr Bool -> Expr a -> Expr a -> Expr adata Expr_ a =
(a ∼ Int) => LitInt_ Int
| (a ∼ Bool) => LitBool_ Bool
| (a ∼ Int) => Add_ (Expr_ Int) (Expr_ Int)
| (a ∼ Bool) => Not_ (Expr_ Bool)
| If_ (Expr_ Bool) (Expr_ a) (Expr_ a)Type Families
{#- LANGUAGE TypeFamilies -#}Closed Type Families
-
We can manually “promote” term-level functions by writing a closed type family
- Can't automatically promote term-level functions into type-level ones (like data constructors)
- Explicitly duplicate term level logic
or :: Bool -> Bool -> Bool
or True _ = True
or False y = y
type family Or (x :: Bool) (y :: Bool) :: Bool where
Or 'True y = 'True
Or 'False y = yOpen Type Families
- Like closed type families but you can keep adding type instances
or :: Bool -> Bool -> Bool
or True _ = True
or False y = y
type family Or (x :: Bool) (y :: Bool) :: Bool
type instance Or 'True y = 'True
type instance Or 'False y = ySaturation
- Type families must be fully "saturated"
- No type-level currying
- AKA no partial application
- No type-level currying
- We can write a type level Map compiles but we can't use it
type family Map (x :: a -> b) (i :: [a]) :: [b] where
Map f '[] = '[]
Map f (x ': xs) = f x ': Map f xs
-- λ> :t undefined :: Proxy (Map (Or 'True)
-- '[ 'True, 'False , 'False ])
-- <interactive>:1:14: error:
-- • The type family ‘Or’ should have 2 arguments,
-- but has been given 1....Associated Type Families
- Type families associated with a typeclass
- Because typeclasses are our means of providing ad-hoc polymorphism, associated type families allow us to compute ad-hoc types.
- Associated type families are always open
class Collection c where
type Elem c :: *
firstElem :: c -> Elem c
instance Collection [a] where
type Elem [a] = a
firstElem (x:xs) = x
instance Collection (a,b) where
type Elem (a,b) = a
firstElem (x,y) = xAssociated Type Families
- The type indexes corresponding to class parameters must be identical to the type given in the instance head
- If an associated family instance is omitted, the corresponding instance type is not inhabited
class Collection c where
type Elem c :: *
firstElem :: c -> Elem c
instance Collection [a] where
type Elem [a] = a
firstElem (x:xs) = x
instance Collection (a,b) where
firstElem _ = undefined
-- <interactive>:614:1: warning: [-Wmissing-methods]
-- • No explicit associated type or default...Type Variables
Scope and Application
Visible Type Applications
- Like type annotations but better
- An argument of the form @ty specifies a type argument
- You can avoid applying a type with an underscore
- Types are applied in the same order they appear in a type signature (including context and forall quantifiers)
λ> :t fmap
fmap :: Functor f => (a -> b) -> f a -> f b
λ> :t fmap @_ @Int @Bool
fmap @_ @Int @Bool :: Functor w => (Int -> Bool)
-> w Int
-> w Bool{#- LANGUAGE TypeApplications -#}This compiles :)
prefix :: a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
where xcons ys = x : ysThis doesn't compile!! Why?
prefix :: a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
where xcons :: [a] -> [a]
xcons ys = x : ysFixed!
{-# LANGUAGE ScopedTypeVariables #-}
prefix :: forall a. a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
where xcons :: [a] -> [a]
xcons ys = x : ysScoped Type Variables
- Provides lexically scoped type variables
- Quantifies a for everything "under" prefix
{#- LANGUAGE ScopedTypeVariables -#}{-# LANGUAGE ScopedTypeVariables #-}
prefix :: forall a. a -> [[a]] -> [[a]]
prefix x yss = map xcons yss
where xcons :: [a] -> [a]
xcons ys = x : ysNeed for Type Annotations
- Machine-checked documentation
- As Haskell’s type system becomes increasingly expressive, complete type inference becomes intractable
- type system necessarily relies on programmer-supplied type annotations.
Type-class ambiguity
normalize :: String -> String
normalize s = show (read s)normalize s = show (read s :: Int)Doesn't compile
COMPILES!!!!!!!!!!!!!!!!!!!!!!
λ> :t read
read :: Read a => String -> a
λ> :t show
show :: Show a => a -> String
λ> :t show . read
show . read :: String -> StringConsider:
Polymorphic Recursion
data T a = Leaf a | Node (T [a]) (T [a])
leaves :: T a -> [a]
leaves (Leaf x) = [x]
leaves (Node t1 t2) = concat (leaves t1 ++ leaves t2)
-- λ> leaves (Leaf x) = [x]
-- λ> leaves (Node t1 t2) = concat (leaves t1 ++ leaves t2)
--
-- <interactive>:152:1: error:
-- • Occurs check: cannot construct the infinite type: a ~ [a]
-- Expected type: T [a] -> [[a1]]
-- Actual type: T a -> [a1]
-- • Relevant bindings include
-- leaves :: T [a] -> [[a1]] (bound at <interactive>:152:1)- Type inference for polymorphic recursion is undecidable and requires programmer supplied type annotations
GADTS
data G a where
MkInt :: G Int
MkFun :: G (Int -> Int)
matchG :: G a -> a
matchG MkInt = 5
matchG MkFun = (+10)- matchG won't type-check without type signature
- When we learn that a value g :: G a is actually the constructor MkInt, then we simultaneously learn that a really is Int
Ambiguous Types
type family F a
type instance F Bool = Char
ambig :: Typeable a => F a -> Int
ambig _ = 5
test :: Char -> Int
test x = ambig @Bool x- In test, GHC must decide what type should instantiate the a in ambig’s type. Any choice a = τ must ensure that F τ ∼ Char but, because F might not be injective, that does not tell us what a should be.
- A type signature isn't enough, we need TypeApplications
Rank Polymorphism
{#- LANGUAGE RankNTypes -#}Rank Polymorphism

Example
applyToFive :: (a -> a) -> Int
applyToFive f = f 5
-- <interactive>:650:17: error:
-- • Couldn't match expected type
-- ‘Int’ with actual type ‘a’
Won't compile :(
applyToFive :: (forall a. a -> a) -> Int
applyToFive f = f 5
-- λ> applyToFive id
-- 5Compiles! :)
Rank Polymorphism
-
Rank
- the rank of a function is the “depth” of its polymorphism
- A function that has no polymorphic parameters is rank 0
- Most common functions are rank 1
- any function above rank-1 to be rank-n or higher rank
- the rank of a function is the “depth” of its polymorphism
-
Rank Polymorphism
- Makes polymorphism first class
- In general, type inference is undecidable in the presence of higher-rank polymorphism
- higher-rank polymorphism always requires an explicit type signature.
Rank Polymorphism
-
Higher-rank types
- functions which take callbacks.
- The rank of a function is how often control gets “handed off”
- A rank-2 function will call a polymorphic function for you
- A rank-3 function will run a callback which itself runs a callback
Rank Polymorphism
Consider:
foo :: forall r. (forall a. a -> r) -> r
foo fn = _We get to determine the return type r, but we never get implementation of whatever fn is get to decide what a is
Counting Rank
- The rank of a function is simply the number of arrows its deepest forall is to the left of
- The forall quantifier binds more loosely than the arrow type (->), so forall a. a -> a is forall a. (a -> a)
What are the ranks of foo, bar, and baz?
foo :: Int -> forall a. a -> a
bar :: (a -> b) -> (forall c. c -> a) -> b
baz :: ((forall x. m x -> b (z m x))
-> b (z m a))
-> m aCounting Rank
- The rank of a function is simply the number of arrows its deepest forall is to the left of
- The forall quantifier binds more loosely than the arrow type (->), so forall a. a -> a is forall a. (a -> a)
foo :: Int -> forall a. a -> a -- rank 1
bar :: (a -> b) -> (forall c. c -> a) -> b -- rank-2
baz :: ((forall x. m x -> b (z m x)) -- rank-3
-> b (z m a))
-> m aFirst Class Families
Defunctionalization
- the process of replacing an instantiation of a polymorphic function with a specialized label instead
fst :: (a, b) -> a
fst (a, b) = a
-- Defunctionalized
data Fst a b = Fst (a, b)
class Eval l t | l -> t where
eval :: l -> t
instance Eval (Fst a b) a where
eval (Fst (a, b)) = a
-- λ> eval $ Fst (10,20)
-- 10Defunctionalizing Higher Order Functions
type family Map (x :: a -> b) (i :: [a]) :: [b] where
Map f '[] = '[]
Map f (x ': xs) = f x ': Map f xs
Type-Level Defunctionalization
type Exp a = a -> Type
type family Eval (e :: Exp a) :: a
data Snd :: (a, b) -> Exp b
type instance Eval (Snd '(a, b)) = b
-- λ> :kind! Eval (Snd '(1, " hello " ))
-- Eval (Snd '(1, " hello " )) :: Symbol
-- = " hello "More
-------------------------------------------
-- Term Level
data Optional a = Missing | Present a
fromOptional :: a -> Optional a -> a
fromOptional deflt Missing = deflt
fromOptional deflt (Present a) = a
-------------------------------------------
-- Type Level
import qualified GHC.TypeLits as TL
data FromOptional :: k -> Optional k -> Exp k
type instance Eval (FromOptional a 'Missing) = a
type instance Eval (FromOptional _a ('Present b)) = b
data Plus :: TL.Nat -> TL.Nat -> Exp TL.Nat
type instance Eval (Plus a b) = a TL.+ bMore
-------------------------------------------
-- Term Level
data Optional a = Missing | Present a
fromOptional :: a -> Optional a -> a
fromOptional deflt Missing = deflt
fromOptional deflt (Present a) = a
-------------------------------------------
-- Type Level
import qualified GHC.TypeLits as TL
data FromOptional :: k -> Optional k -> Exp k
type instance Eval (FromOptional a 'Missing) = a
type instance Eval (FromOptional _a ('Present b)) = b
data Plus :: TL.Nat -> TL.Nat -> Exp TL.Nat
type instance Eval (Plus a b) = a TL.+ bHigher Order Type Functions
data Optional a = Missing | Present a
data FromOptional :: k -> Optional k -> Exp k
type instance Eval (FromOptional a 'Missing) = a
type instance Eval (FromOptional _a ('Present b)) = b
-- λ> :kind! Eval (Map (FromOptional 3)
-- [ 'Present 1, 'Present 2, 'Missing])
-- Eval (Map (FromOptional 3)
-- [ 'Present 1, 'Present 2, 'Missing]) :: [GHC.Types.Nat]
-- = '[1, 2, 3]- While you can't use Type Families with partially applied types, you can use type level defunctionalization
First Class Families
λ> :kind! Eval ((Snd <=< FromMaybe '(0, 0))
=<< Pure (Just '(1,2)))
Eval ((Snd <=< FromMaybe '(0, 0))
=<< Pure (Just '(1,2))) :: Nat
= 2- Package called first-class-families
- Provides:
- (Single) Open type family Eval
- Kind constructor Exp
- Forms a type-level monad
- Variety of Prelude functions as defunctionalized data declarations with Eval type instances
{-# LANGUAGE DataKinds, PolyKinds, TypeFamilies,
TypeInType, TypeOperators, UndecidableInstances #-}What's Next?
What's Next?
- Type Variables in Patterns
- Visible Type on the LHS
- Binding Type Variables in Lambdas
- FCF Expansion
- Dependent Haskell
Title Text
Resources
-
Introductory
- Basic Type Level Programming (Blog)
- Thinking With Types (Book)
-
Type Variables
- Type Variables in Patterns (Paper)
- Servant
-
First Class Families
- Haskell with one Type Family (blog)
- Future
Type Level Programming
By Heneli Kailahi
Type Level Programming
- 567



