Bottom-up mechanisms for the emergence of swarming


Henry Charlesworth (H.Charlesworth@warwick.ac.uk)
International Soft Matter Conference, Edinburgh, June 4th
Supervisor: Professor Matthew Turner
About me

- PhD student in the Centre for Complexity Science, University of Warwick (recently finished).
- Supervised by Professor Matthew Turner (Physics, Centre for Complexity Science)

Motivation
- Been thinking about a potentially general, task-independent principle for decision making - "Future State Maximisation" (FSM) - can this be used as the basis for such a model?
- Can we come up with a collective motion model based on a single, low-level principle, without hard-coding "empirical" features such as alignment and cohesion.
Future State Maximisation (FSM)
- Loosely speaking: "all else being equal, it is preferable to make decisions that keep your options open".
- That is, make decisions that maximise the number of possible things that you can potentially do in the future.
- Rationale is that in an uncertain world, maximising the number of things you're able to do in the future gives you the most control over your environment - puts you in a position where you are most prepared to deal with many different possible scenarios.
FSM - Simple, high-level examples
- Owning a car vs. not owning a car



- Going to university
- Aiming to be healthy rather than sick



- Aiming to be rich rather than poor

Future State Maximisation (FSM)
- In principle, achieving "mastery" over your environment in terms of maximising the control you have over the future things that you can do should naturally lead to: developing re-usable skills, obtaining knowledge about how your environment works, etc.
- Could also be useful as a proxy to evolutionary fitness in many situations. Achieving more control over what it is potentially able to do is almost always beneficial.
How can FSM be useful?
- If you accept this is often a sensible principle to follow, we might expect behaviours/heuristics to have evolved that make it seem like an organism is applying FSM.
Could be useful in explaining/understanding
certain animal behaviours.

- Could also be used to generate behaviour for artificially intelligent agents.
Can FSM be useful in understanding collective motion?
Our work:
"Intrinsically Motivated Collective Motion"

Existing Collective Motion Models
- Often only include local interactions - do not account for long-ranged interactions, like vision (some exceptions).
- Can argue that they lack low-level explanatory power - the models are essentially empirical in that they have things like co-alignment and cohesion hard-wired into them.

Example: Vicsek Model
T. Vicsek et al., Phys. Rev. Lett. 75, 1226 (1995).
R
\mathbf{v}_i(t+1) = \langle \mathbf{v}_k(t) \rangle_{|\mathbf{r}_k-\mathbf{r}_i| < R} + \eta(t)
\mathbf{r}_i(t+1) = \mathbf{r}_i(t) + \mathbf{v}_i(t)
Our approach
- Based on a simple, low-level motivational principle - FSM.
- No built in alignment/cohesive interactions - these things emerge spontaneously.
Our Model
- Consider a group of circular agents equipped with simple visual sensors, moving around on an infinite 2D plane.

Possible Actions:
Visual State
Making a decision
Leads to robust collective motion
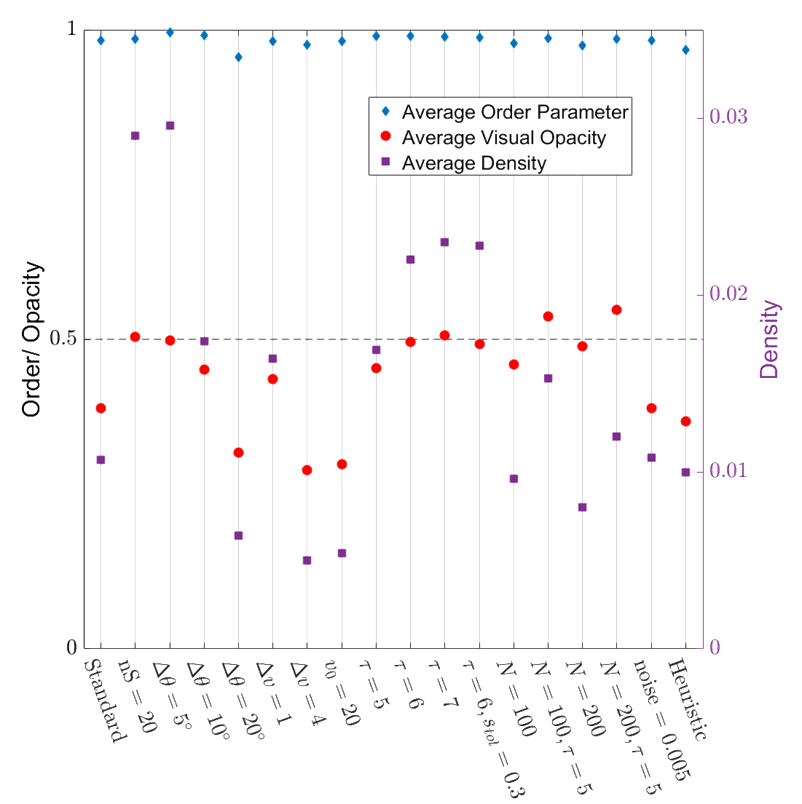
- Very highly ordered collective motion. (Average order parameter ~ 0.98)
- Density is well regulated, flock is marginally opaque.
- These properties are robust over variations in the model parameters!
Scale Free Correlations!
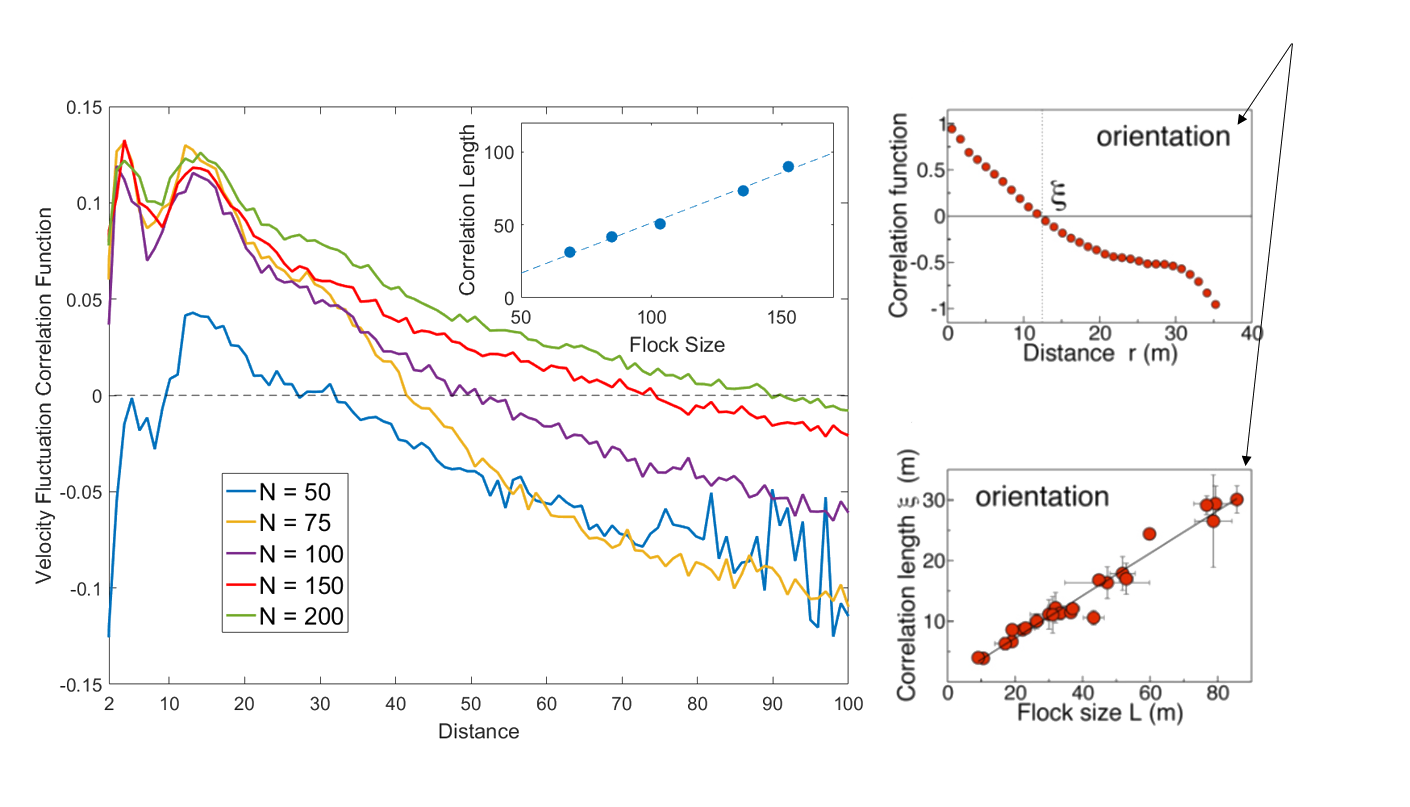
Real starling data (Cavagna et al. 2010)
Data from model
- Scale free correlations mean an enhanced global response to environmental perturbations!
\mathbf{u_i} = \mathbf{v_i} - \langle \mathbf{v} \rangle
correlation function:
C(r) = \langle \mathbf{u}_i(0) . \mathbf{u}_j(|r|) \rangle
velocity fluctuation
Continuous version of the model
- Would be nice to not have to break the agents' visual fields into an arbitary number of sensors.
- Cannot count continuous visual states - need to do something a bit different.

Continuous version of the model

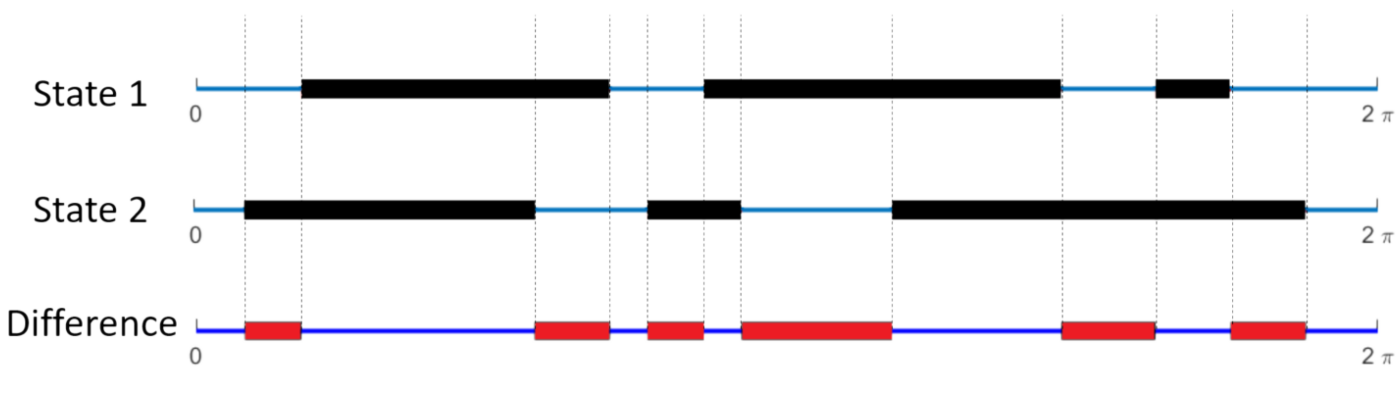
- Let \(f(\theta)\) to be 1 if angle \(\theta\) is occupied by the projection of another agent, or 0 otherwise
- Define the "difference" between two visual states i and j to be:
d_{ij} = \frac{1}{2\pi} \int_0^{2\pi} [f_i(\theta)(1-f_j(\theta)) + f_j(\theta)(1-f_i(\theta))]d\theta
- This is simply the fraction of the angular interval \([0, 2\pi)\) where they are different.
Continuous version of the model
W_{\alpha} = \frac{1}{n_{\alpha}} \sum_{i=1}^{n_{\alpha}} \sum_{j=1}^{n_{\alpha}} d_{ij}
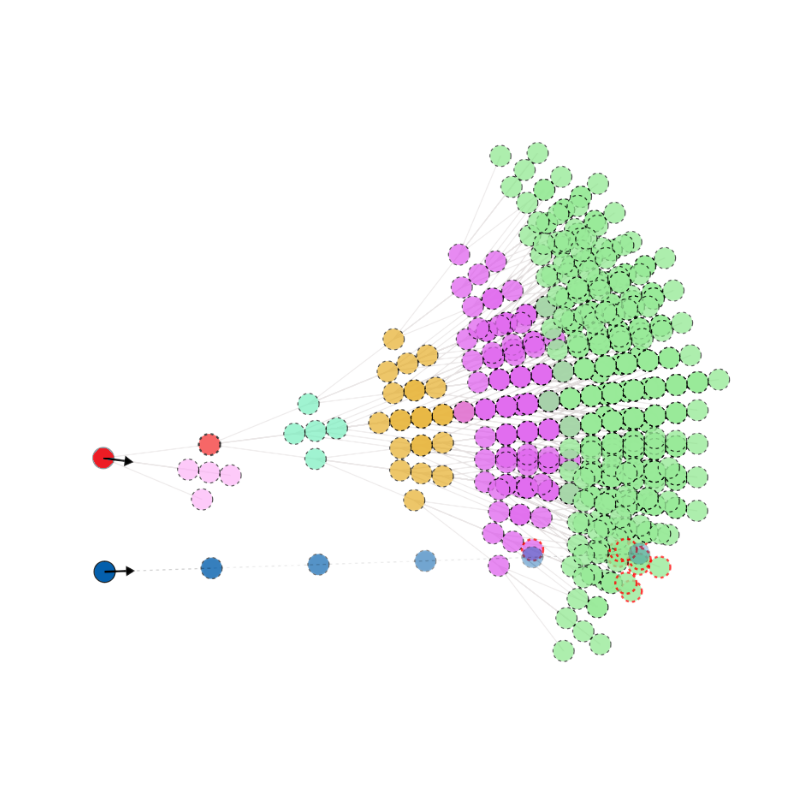
branch \(\alpha\)
For each initial move, \( \alpha \), define a weight as follows:
- Rather than counting the number of distinct visual states on each branch, this weights every possible future state by its average difference between all other states on the same branch.
- Underlying philosophy of FSM remains the same.
Result with a larger flock - rich emergent dynamics
Can we do this without a full search of future
- This algorithm is very computationally expensive. Can we generate a heuristic that acts to mimic this behaviour?
- Train a neural network on trajectories generated by the FSM algorithm to learn which actions it takes, given only the currently available visual information (i.e. no modelling of future trajectories).
states?
Visualisation of the neural network
previous visual sensor input
current visual sensor input
hidden layers of neurons
output: predicted probability of action
non-linear activation function: f(Aw+b)
How does it do?
Conclusions
- FSM might be a useful principle for understanding/generating a wide range of interesting behaviour - very general, can be applied to any agent-environment interaction.
- Demonstrated that a simple model based on this principle leads to the emergence of a realistic swarm.
- Looked at trying to train a heuristic that mimics FSM which is simple enough to plausibly operate under animal cognition.
Thanks for listening!
Bottom-up-swarming
By Henry Charlesworth
Bottom-up-swarming
- 1,322



