Rasterization,

Hidden Surface Removal

and

OpenGL Buffers

Speaker  : 羅右鈞

Date        : 2015.8.4

Location : 交通大學

Rasterization

- Or called Scan conversion

- Convert primitives to fragments (potential pixels)

- We will focus on how to do line drawing and polygon filling

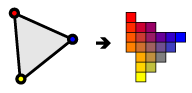
Rasterization

Line drawing

    - DDA

    - Bresenham's Algorithm

Polygon filling

    - Flood Fill

DDA (Digital Differential Analyzer)

- Simplest line drawing algorithm

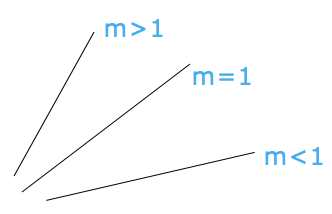
- Basic idea : 

using precalculated slope m by two given endpoints, and

when m >= 1 : increment x by 1, find the best y in each iteration

when m < 1   : increment y by 1, find the best x in each iteration

(we ignore negative slope)

DDA (Digital Differential Analyzer)

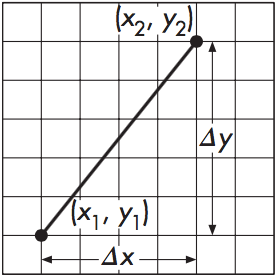
Assume write_pixel (int x, int y, int color) .

given two endpoints (x1, y1) , (x2, y2) ,

we can get the slope :

m = (y2 - y1) / (x2 - x1)

=> m = △y / △x

=> △y = m△x 

DDA (Digital Differential Analyzer)

Assume 0 <= m <= 1,

we increment x by 1, find the best y in each iteration :

for ( x = x1 ; x <= x2 ; x++ ) {
    y += m;
    write_pixel ( x, round(y), color ); // 由於 m 可能是浮點數，需對y做四捨五入找出最適當的pixel位置
}

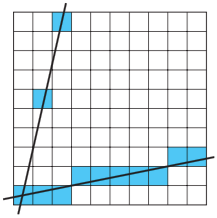
then we get the result :

DDA (Digital Differential Analyzer)

The result is not good enough when m > 1,

so when m > 1, we need to change our method to 

increment y by 1, find the best x in each iteration.

(not optimized)

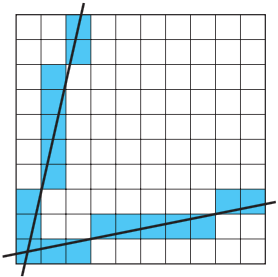
(optimized)

Bresenham's Algorithm

Optimized DDA algorithm (avoid floating-point operation) .

Given two endpoints (x0, y0) , (x1, y1) , assume :

- x1 > x0

- line equation : y = mx + b

- 0 <= m <= 1, where m is slope

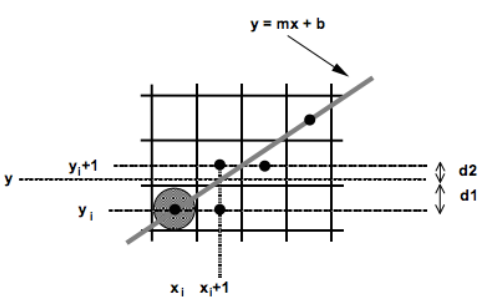
Bresenham's Algorithm

In this case, we increment x by 1 and find the best y, just same as DDA .

Assume we currently finish processing the pixel (xi, yi) .

We want to find the next position of pixel (xi+1, yi+1) .

xi+1 = xi + 1, since we increment x by 1.

we need to determine y = yi or yi + 1 (remain y or increment y by 1) .

Bresenham's Algorithm

Define :

- d1 = y - yi

- d2 = (yi + 1) - y

Since y = m(xi + 1) + b when x = xi + 1 (by y = mx + b) ,

we get :

- d1 = m(xi + 1) + b - yi

- d2 = (yi + 1) - m(xi + 1) - b

d1 - d2 = m(xi + 1) + b - yi - yi - 1 + m(xi + 1) + b

= 2m(xi + 1) - 2yi + 2b - 1

Bresenham's Algorithm

How to determine yi+1 ?

When d1 - d2 < 0 , yi+1 = yi (remain y)

When d1 - d2 > 0 , yi+1 = yi + 1 (increment y by 1)

Bresenham's Algorithm

How to avoid floating-point operation ?

We simply multiply △x to m = △y /△x​ to eliminate denominator.

We apply this to d1 - d2 = 2m(xi + 1) - 2yi + 2b - 1 :

Assume pi = △x (d1 - d2)

= △x [ 2m( xi + 1 ) - 2yi + 2b - 1 ]

= △x [ 2・(△y / △x)・( xi + 1 ) - 2yi + 2b - 1 ] ( by m = △y / △x )

= 2△y ( xi + 1 ) - 2△x・yi + 2△x・b - △x ( by multiplying △x )

= 2△y・xi + 2△y - 2△x・yi + 2△x・b - △x

= 2△y・xi - 2△x・yi + 2△y + 2△x・b - △x

The blue part is constant in every iteration, we can simplify as 

pi = 2△y・xi - 2△x・yi + c

Bresenham's Algorithm

Since determine d1 - d2 is positive or negative to pick the best y

= determine pi is positive or negative

pi = 2△y・xi - 2△x・yi + c

pi+1 = 2△y・xi+1 - 2△x・yi+1 + c

pi+1 - pi

= 2△y・xi+1 - 2△x・yi+1 + c - (2△y・xi - 2△x・yi + c)

= 2△y・(xi+1 - xi) - 2△x・(yi+1 - yi)  ( xi+1 - xi ＝ 1, since we increment x by 1)

= 2△y - 2△x・(yi+1 - yi) 

Finally we get pi+1 = pi + 2△y - 2△x・(yi+1 - yi) 

The blue part is either 0 (pi < 0) or 1(pi > 0)

Bresenham's Algorithm

In conclusion :

- when pi < 0 , pi+1 = pi + 2△y , since yi+1 - yi = 0

- when pi > 0 , pi+1 = pi + 2△y - 2△x , since yi+1 - yi = 1

So we only need to calculate the initial p ,

then in every iteration , we calculate next p by the below formula to

determine the next pixel position ( find the best y ) .

we know that pi = 2△y・xi - 2△x・yi + 2△y + 2△x・b - △x

p0 (initial p)

= 2△y・x0 - 2△x・y0 + 2△y + 2△x・b - △x

= 2△y・x0 - 2△x・y0 + 2△y + 2△x・[ y0 - (△y / △x)・x0 ] - △x

( by  y0 = m・x0 + b => b = y0 - (△y / △x)・x0 )

= 2△y - 2△x

Bresenham's Algorithm

So, this is how it works :

1. given two endpoints (x0, y0) , (x1, y1)

2. calculate constants :

    - △x = x1 - x0 and △y = y1 - y0

    - 2△x and 2△y

    - p0 = 2△y - 2△x

3. draw pixel ( round(x0), round(y0) )

4. for x = x0 to x1, i = 0 {
        if ( pi < 0 ) , write_pixel (xi + 1, yi, color) , pi+1 =  pi + 2△y

        else           , write_pixel (xi + 1, yi + 1, color) , pi+1 =  pi + 2△y - 2△x

        increment i

    }

Polygon Rasterization

Hollow polygon : 

use Bresenham's algorithm or another line drawing algorithm to draw polygon's edges.

Solid polygon :

use Flood Fill algorithm. 

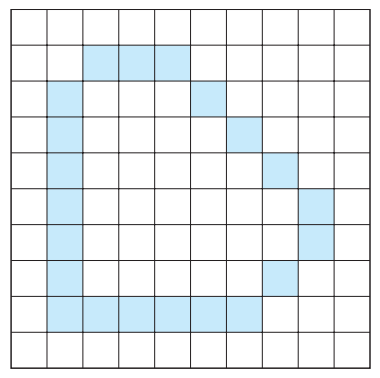
Flood Fill Algorithm

First find the initial point (x,y) (or called seed point) ,

then recursively find the neighbors of the seed point and draw them.

Assume we have a function read_pixel (x, y) to get the pixel color at the position (x, y)

void flood_fill(int x, int y) {
    if ( read_pixel(x,y) == replacement_color ) { 
        write_pixel(x,y,target_color);
        flood_fill(x-1,y);
        flood_fill(x+1,y);
        flood_fill(x,y-1);
        flood_fill(x,y+1);
    }
}

Hidden Surface Removal

- or called visible-surface determination

- determine which fragments are visible

- two approachs :

    - Object space approach , such as Painter algorithm.

    - Image space approach , such as Z-buffer algorithm.

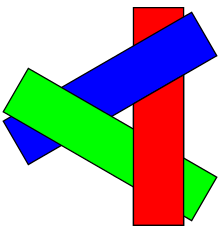
Painter Algorithm

- Or called Priority Fill

- Sort objects depending on their distance to viewer, then draw them from far to near. But whenever object or camera moves, we need to sort again.

- Not work in this case :

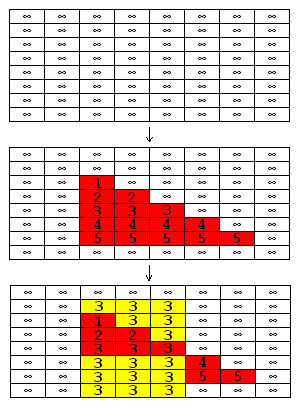
Z-buffer Algorithm

OpenGL Buffers

Frame buffer consists of :

- Color buffer

- Depth buffer

- Stencil buffer

- Accumulation buffer

Color Buffer

- Color buffer consists of :

    - Front buffer

    - Back buffer

- Save pixel's RGB or RGBA values 

( need to set glutInitDisplayMode( GLUT_RGBA ) )

Single buffering

- Set glutInitDisplayMode(GLUT_SINGLE)

- Only use front buffer for display and rendering

- Problem : monitor refreshing and GPU drawing are asynchronized.

Could cause flickering when doing animation.

Double buffering

- Set glutInitDisplayMode(GLUT_DOUBLE)

- Use front buffer for display and back buffer for rendering

- Need to call glutSwapBuffers() in the end of display function

- Also remember to call glClear(GL_COLOR_BUFFER_BIT) to clear the previous drawing

Depth buffer (Z-buffer) 

- Save pixel's depth value

- Need to do in OpenGL :

    - glutInitDisplayMode(GLUT_DEPTH)

​    - glEnable(GL_DEPTH_TEST)

- Use glDepthFunc(GLenum func) to determine how to test depth value.

- Also remember to call glClear(GL_DEPTH_BUFFER_BIT) in the end of display function to clear the previous depth value

Depth buffer (Z-buffer) 

(Cont.) ​Use glDepthFunc(GLenum func) to determine how to test depth value.

GL_NEVER：never pass

GL_LESS：if target pixel's z value < current pixel's z value，then pass (default)

GL_EQUAL：if target pixel's z value = current pixel's z value，then pass

GL_LEQUAL：if target pixel's z value <= current pixel's z value，then pass

GL_GREATER ：if target pixel's z value > current pixel's z value，then pass

GL_NOTEQUAL：if target pixel's z value != current pixel's z value，then pass

GL_GEQUAL：if target pixel's z value = current pixel's z value，then pass

GL_ALWAYS：always pass

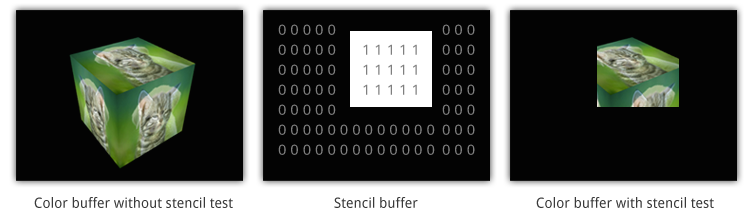
Stencil buffer

- Provide programmer to save extra value in each pixel for customizing.

- Typicall applications : masking and inverted image

More info about how to implement

Accumulation buffer

- Save RGBA color components

- How many bits need to save each color component depend on hardware implementation. You can check it by calling glGetIntegerv

- Use glAccum( GLenum op, GLfloat value ) to manipulate accumulation buffer

Accumulation buffer

- (Cont.) Use glAccum( GLenum op, GLfloat value ) to manipulate accumulation buffer

op can be one of the following values：

GL_ACCUM：從目前選定的color buffer（front 或 back）中讀取值（用glReadBuffer(GL_FRONT 或 GL_BACK) 進行讀取而選定目前的color buffer）用給定的value乘上R、G、B、A值，然後將結果加到accumulation buffer 中。

GL_LOAD：跟GL_ACCUM操作類似，但它是用結果值替換掉accumulation buffer中的值，而不是與之相加。

GL_RETURN：從accumulation buffer中取值，以value乘以該值，然後將該結果放入目前選定的color buffer中。

GL_ADD：將value與accumulation中的每個pixel的R、G、B、A分量相加。

GL_MULT：將value與accumulation中的每個pixel的R、G、B、A分量相乘。

Accumulation buffer

- Typical applications : Motion blur and Anti-aliasing

Without motion blur

With motion blur

Without anti-aliasing

With anti-aliasing