Principle Component Analysis
講者:羅右鈞
日期:2016.10.27
地點:清華大學
Intuition
Let's say, we've collected some data with the following 4 attributes,
and aim to build model to perform some prediction tasks...
| height | dhuwur | altuera | teitei | |
|---|---|---|---|---|
| 0 | 159 | 4.77 | 5.247 | 62.5983 |
| 1 | 168 | 5.04 | 5.544 | 66.1416 |
| ... | ... | ... | ... | ... |
| N | 173 | 5.189 | 5.709 | 68.1101 |
Intuition
In fact ... all these attributes are same as "height" in different languages and be converted to different units
| height | dhuwur | altuera | teitei | |
|---|---|---|---|---|
| 0 | 159 | 4.77 | 5.247 | 62.5983 |
| 1 | 168 | 5.04 | 5.544 | 66.1416 |
| ... | ... | ... | ... | ... |
| N | 173 | 5.189 | 5.709 | 68.1101 |
- "tingg" = "dhuwur" = "altuera" = "teitei" = "height"
- In other words, all attributes are dependent on some quantity which aren't easy to be observed
- We can describe data by only 1 attribute!
Curse of dimensionality
As dimensionality grows: fewer observations per region.
(sparse data)


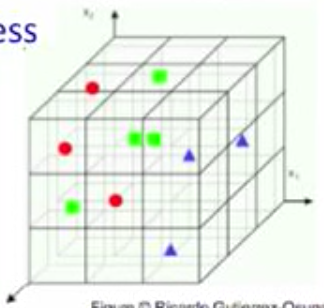
1-D: 3 regions
2-D: 9 regions
3-D: 27 regions
1000-D: GG
That's why dimension reduction is important
Dimension Reduction
Goal: represent instances with fewer variables
- try to preserve as much structure in the data as possible
- we want that structure is useful for specific tasks, e.g., regression, classification.
Feature selection
- pick a subset of the original dimensions X1, X2, X3, ..., Xd-1, Xd
- pick good class "predictors", e.g. information gain
Feature extraction
- Construct a new set of dimensions Ei = f(X1,X2...Xd)
- (linear) combinations of original dimensions
- PCA performs linearly combinations of orignal dimensions
PCA Ideas
Define a set of principle components
- 1st: direction of the greatest variance in data
- 2nd: perpendicular to 1st, greatest variance of what's left
First m << d components become m new dimensions
- You can then project your data with these new dimensions

Why greatest variance?
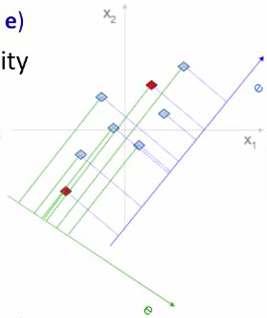
e preserves more structure than e
- distances between data points in original space remains in new space
How to compute Principle Components ?
- Center the data at zero (subtracted by mean)
- Compute covariance matrix Σ
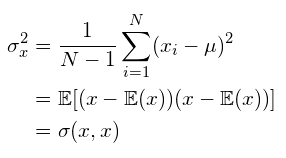
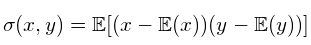
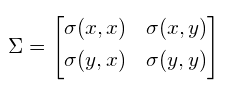
this computes sample variance (N-1 to estimate unbiased variance)
- Normalize(standardize) covariance matrix [-inf, inf] to [-1, 1], we get Pearson correlation coefficient (correlation matrix)
- The correlation coefficient between two random variables x and y are defined as:
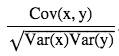
if computing population variance, you can just divide by N
How to compute Principle Components (cont.)?
Interesting observation:
- multiply a vector by covariance matrix
x1
x2
e1
e2
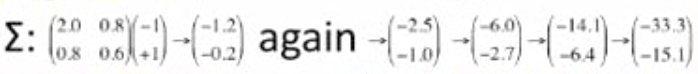
slope: 0.400 0.450 0.454... 0.454...
Want vectors e which aren't rotated: Σe = λe
- principle components = eigenvectors with largest eigenvalues
In fact ... (see Read more for proof)
- eigenvector = direction of greatest variance
- eigenvalue = variance along eigenvector
(-1.0, +1.0)
(-1.2, -0.2)
(-14.1 -6.4)
(-33.3 -15.1)
(-6.0, -2.7)

Finally, project original data points to new dimesions by dot product
Read more
- Principle Component Analysis (Main reference)
- A geometric interpretation of the covariance matrix
- Khanacademy: Introduction to eigenvalues and eigenvectors
- Quara: Why does repeatedly multiplying a vector by a square matrix cause the vector to converge on or along the matrix's eigenvector?
- Quara: What do eigenvalues and eigenvectors represent intuitively?
L1 sentence
Encoder
L1 encoded vector
L2 Decoder
L2
sentence
Encoder
L2
encoded vector
L1 Decoder
Inference
Training
Principle Component Analysis
By Howard Lo
Principle Component Analysis
- 805



