Ihno Schrot — The Story Behind the Professional — December 16th 2025
MY CV
2013 - 2017
Bachelor
Mathematics
Internship
2016
Consultant
2017
Student Assistant
2017
2017 - 2019
Master Scientific
Computing
2019 - 2025
PhD
Numerical
Optimization
Scientist for Optimization Algorithm Development
since 2025
Ihno Schrot — The Story Behind the Professional — December 16th 2025
BACHELOR STUDIES
2013 - 2017 Bachelor Mathematics
PDEs and Cellular Automata for Modelling Inflammatory Processes
Thesis
Integer and Linear Programming
Focus
Physics
Minor
Ihno Schrot — The Story Behind the Professional — December 16th 2025
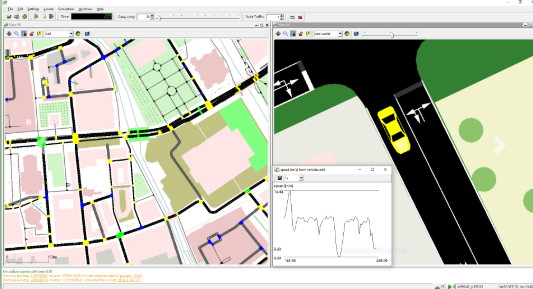
DEUTSCHES ZENTRUM FÜR LUFT- UND RAUMFAHRT
2016/2017 Internship and Student Assistant
Integer
(and a bit Dynamic) Programming
Focus
Algorithms for Dial-a-Ride Problems for the "Reallabor Schorndorf"
Student Assistant
Traffic Light Algorithms
Internship
Ihno Schrot — The Story Behind the Professional — December 16th 2025
SIDEWALK LABS
2017 Consultant
Evaluation and Presentation
Focus
Improving Urban Infrastructure Through Technological Solutions
Purpose
Traffic Light Algorithms
V2X-Communication
Platooning
Traffic Simulations
Ihno Schrot — The Story Behind the Professional — December 16th 2025
PHD STUDIES
2019 - 2025 PhD Numerical Optimization
Application
Algorithms
Theory
Teaching
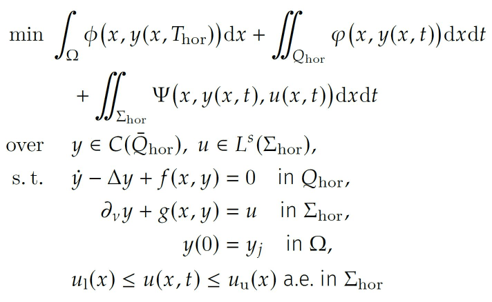
Ihno Schrot — The Story Behind the Professional — December 16th 2025
MOTIVATION FOR MY PHD PROJECT
Bildquellen: jcomp, bzw. rawpixel.com, auf Freepik
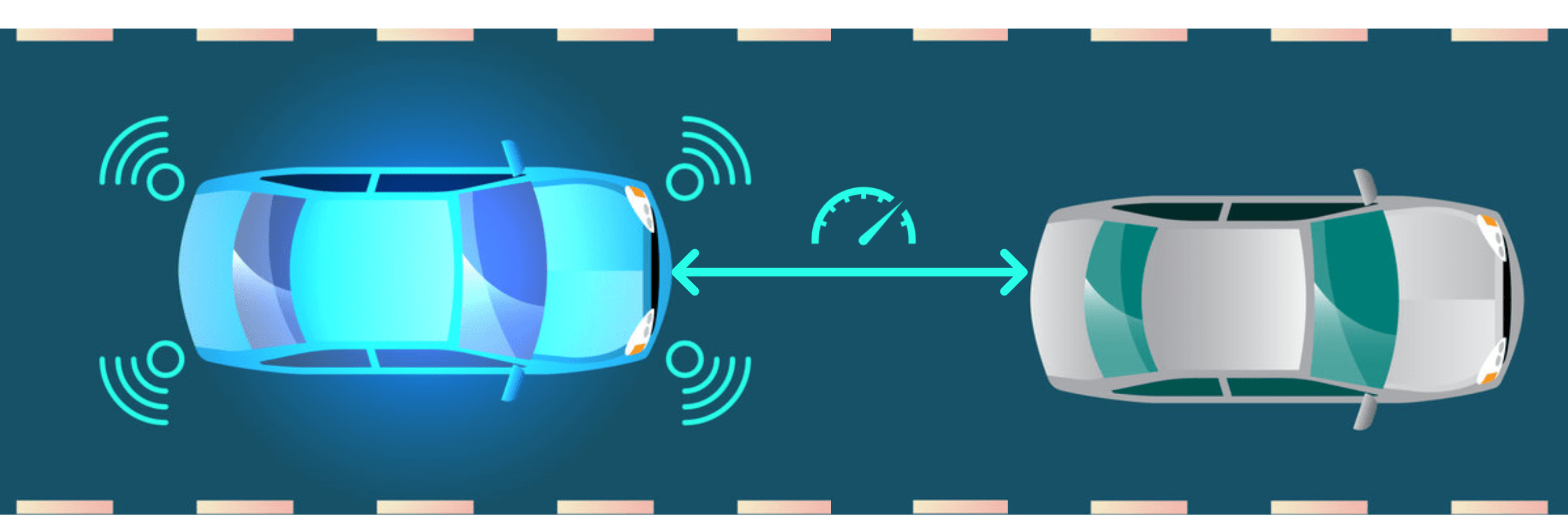
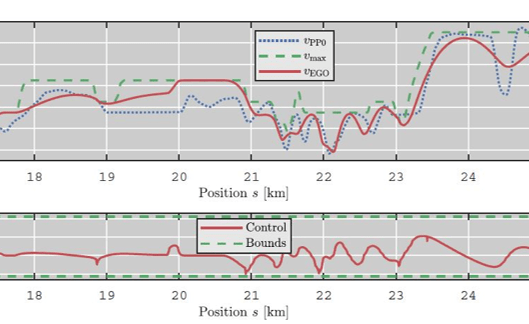
Adaptive Cruise Control (ACC)
- Driving Assistance System
- Cruise Control + Distance Control
Ecological ACC (EACC)
- Vary distance to preceding vehicle (PP0)
- Leverage traffic and route data \(\rightarrow\) Save energy
\(\rightarrow\) Nonlinear Model Predictive Control (NMPC)
- Handling tabulated data and external inputs
- Limited computational power of onboard hardware
Challenges for Numerical NMPC Methods
NONLINEAR MODEL PREDICTIVE CONTROL (NMPC)
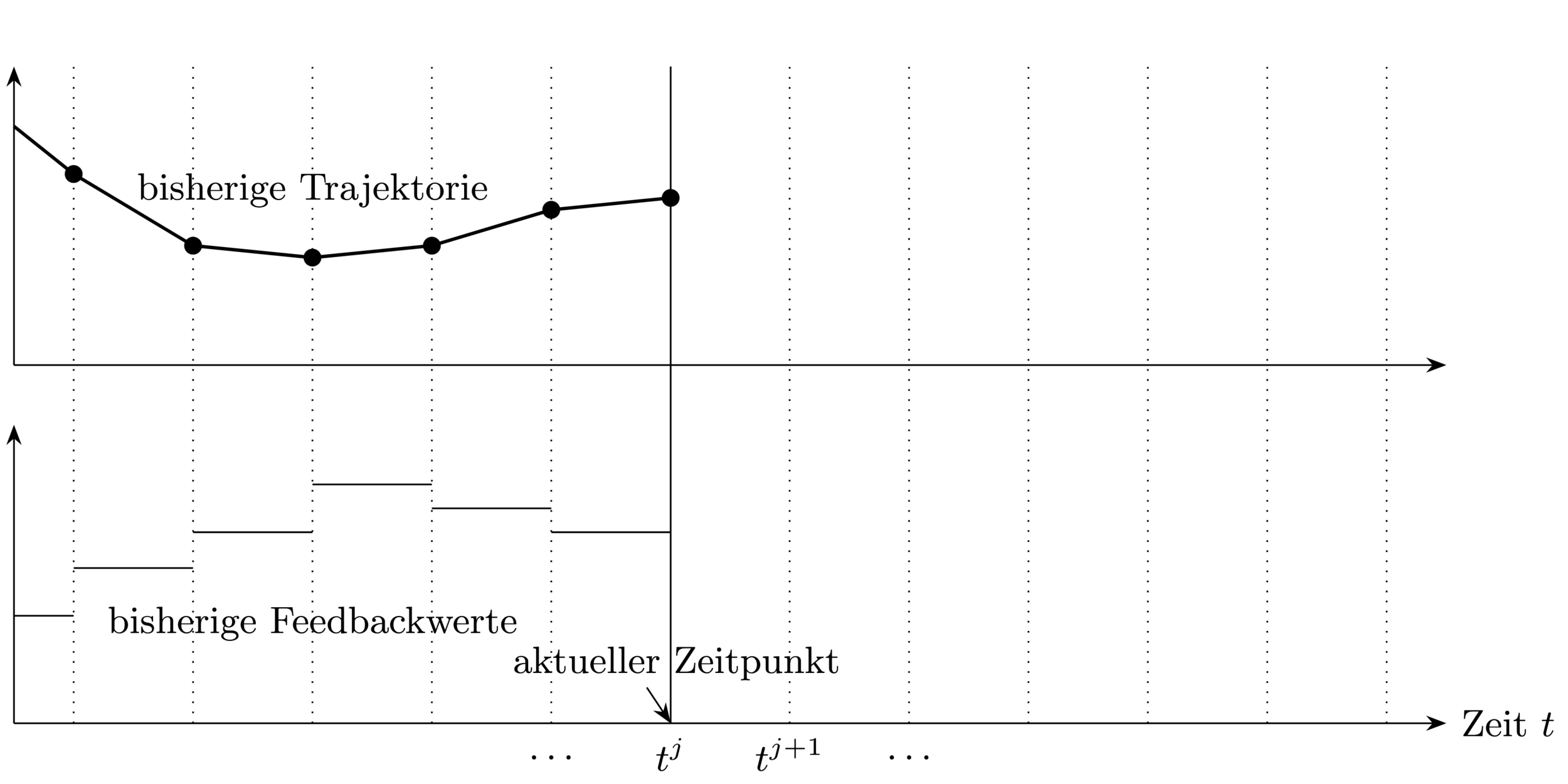
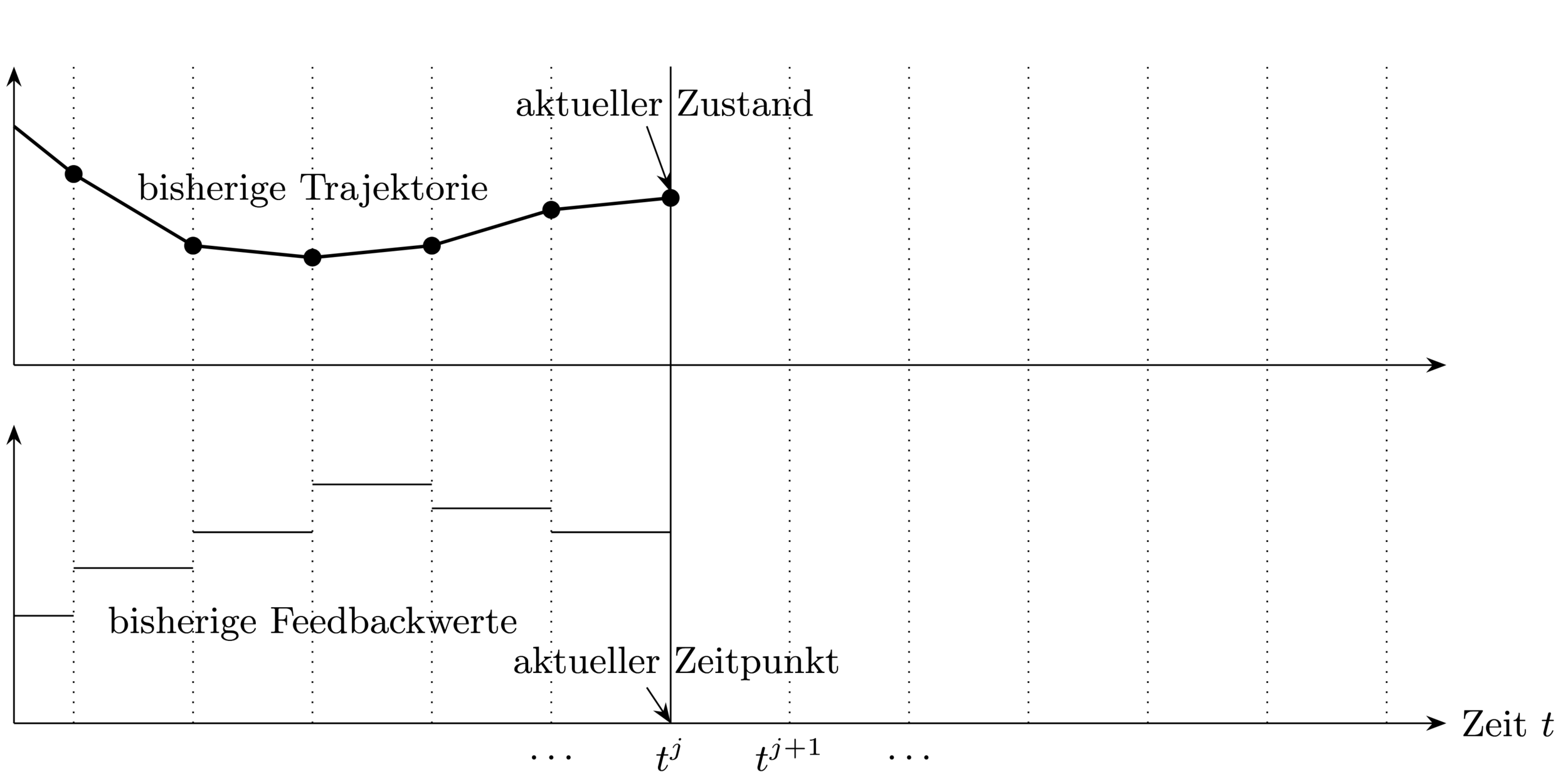
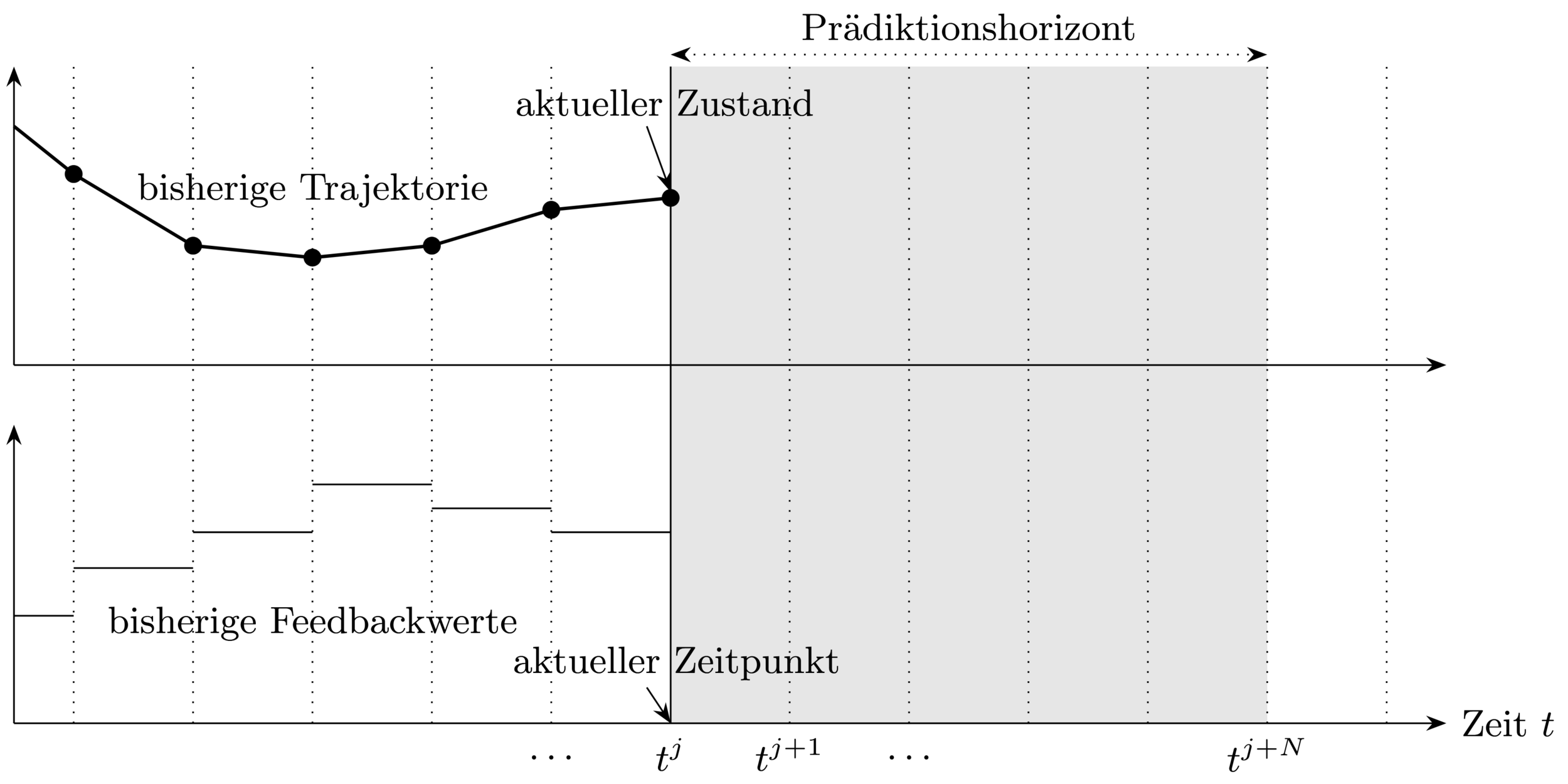
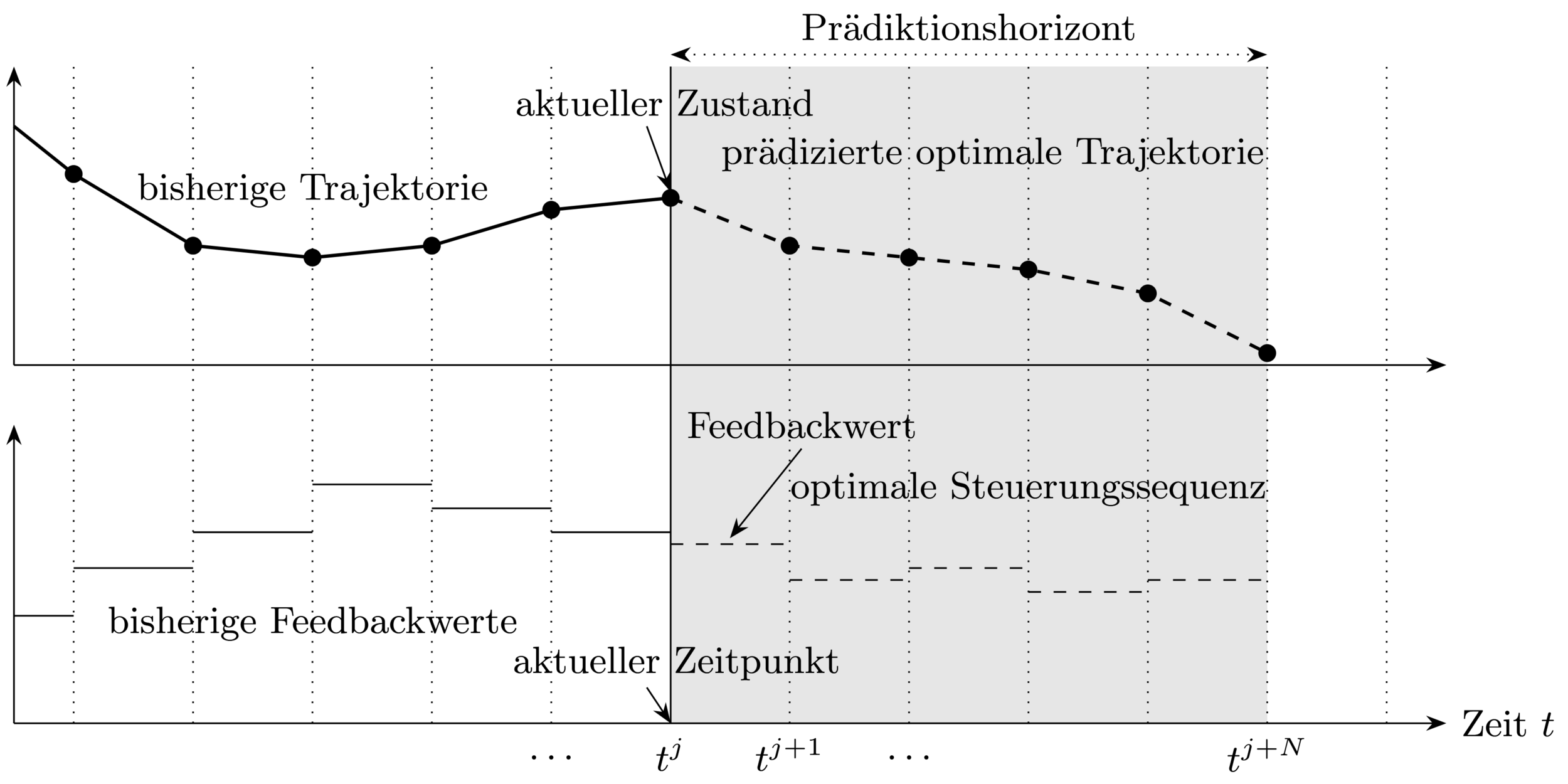
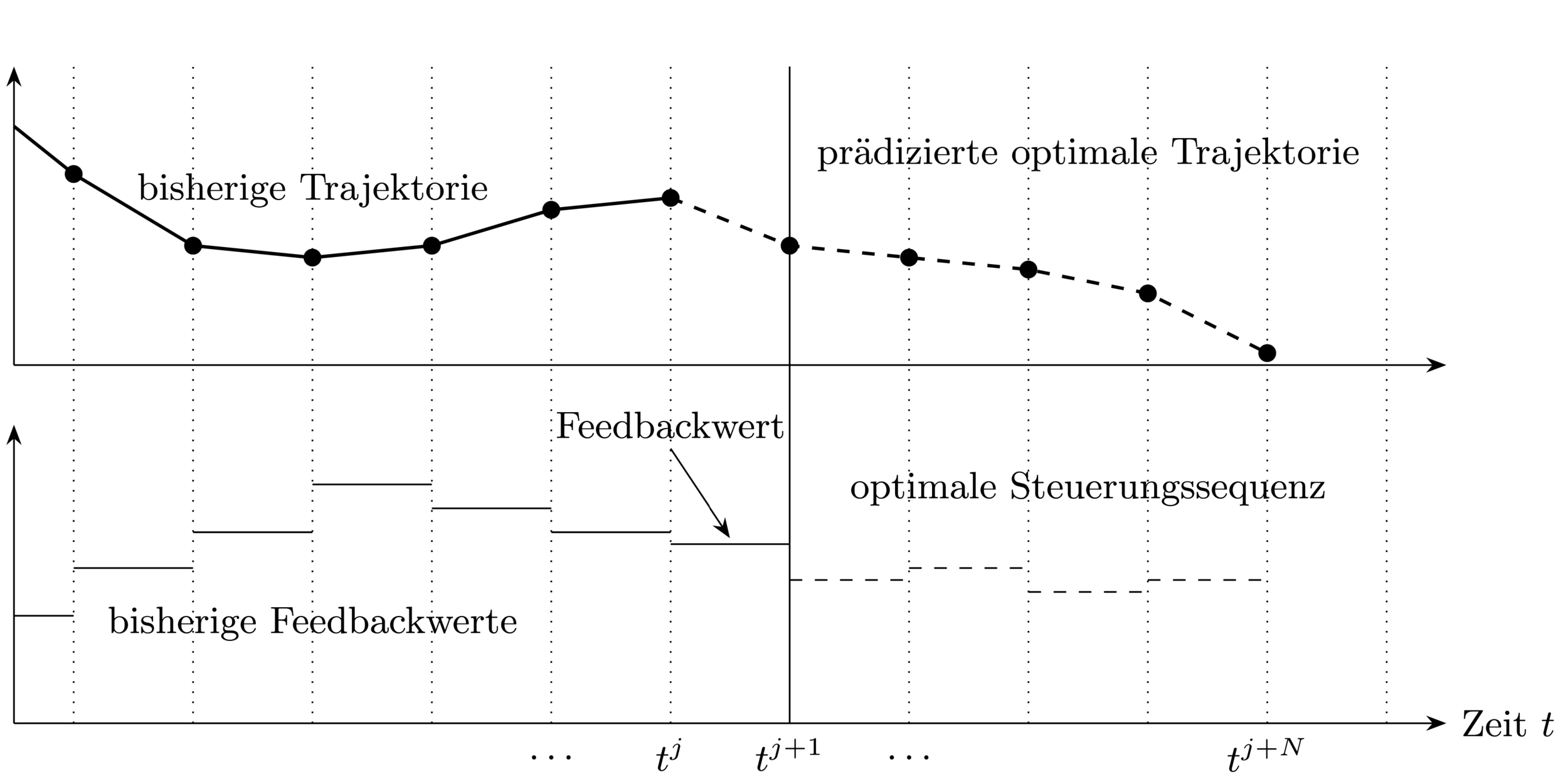
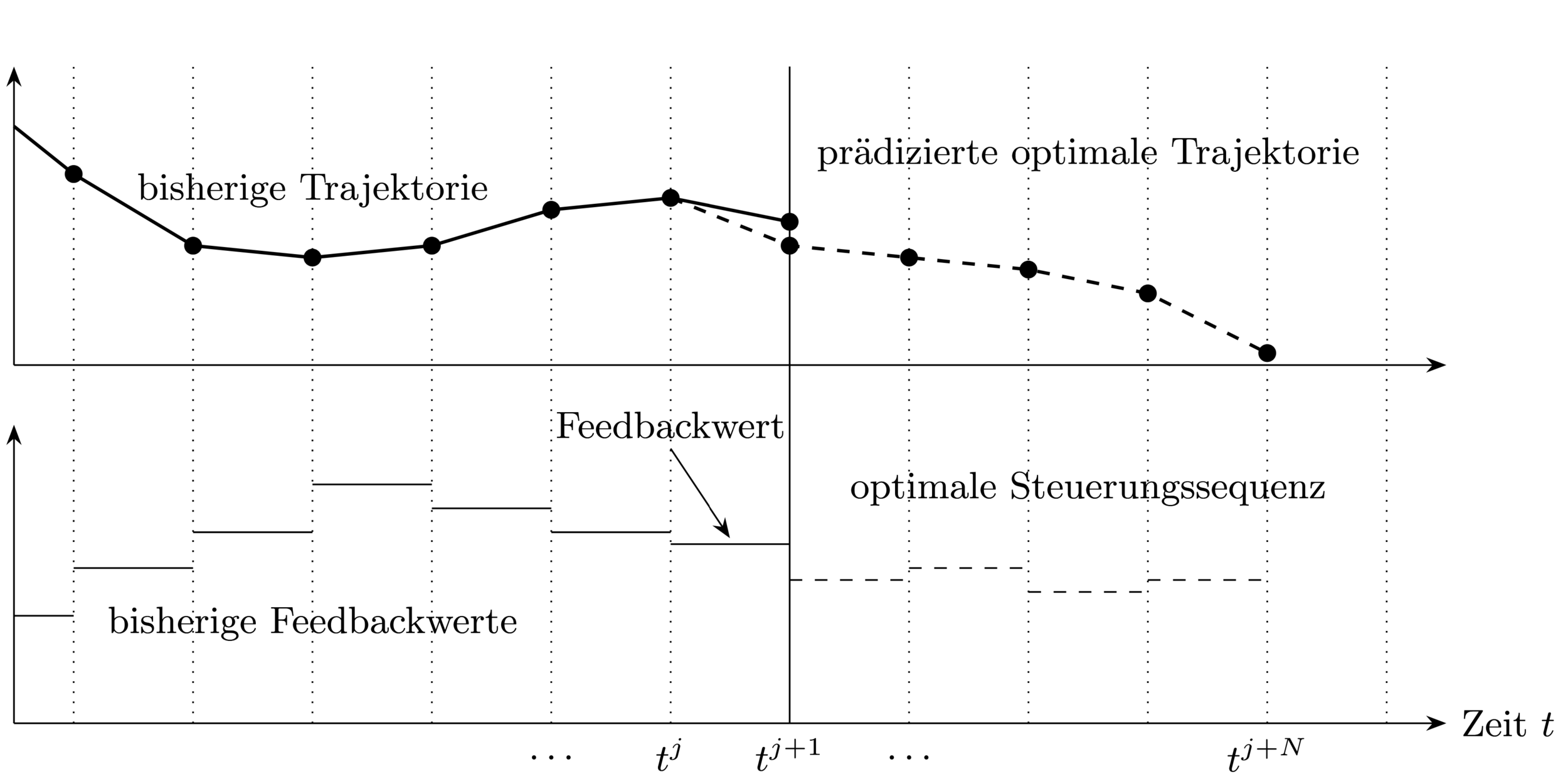
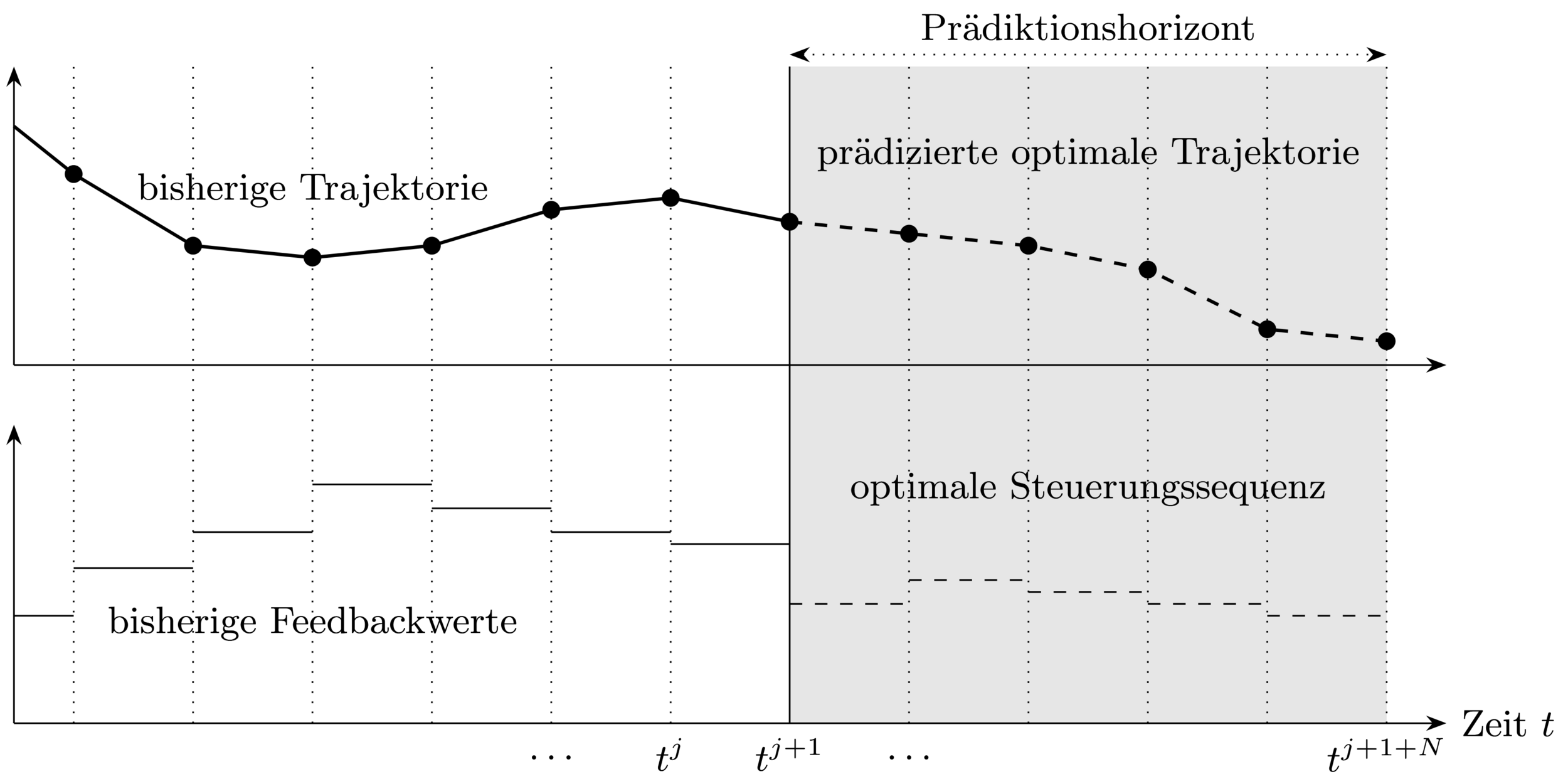
At each sampling time point:
1. Get current state
3. Use feedback value until next
sampling time point
2. Solve optimal control problem (OCP) over
prediction horizon
Closed-loop Control Strategy \(\rightarrow\) allows to react to disturbances
Ihno Schrot — The Story Behind the Professional — December 16th 2025
FRAMEWORK TO EFFICIENTLY SOLVE PARAMETRIZED OCPS
\newcommand{\ud}{\mathrm{d}}
\begin{aligned}
&\min_{x(\cdot),u(\cdot)} & \int_{t^j}^{t^j+T} &\Psi\left(x(t),u(t)\right) \ud t +
\Phi\left(x(t^j+T)\right)\\
&\quad\text{s.\,t. }& \dot{x}(t) &= f\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T],\\
&& x(t^j) &= x^j,&&\\
&& 0 &\leq h\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T],\\
&& 0 &= r^{\mathrm{e}} \left(x(t^j),x(t^j+T)\right),\\
&& 0 &\leq r^{\mathrm{i}} \left(x(t^j),x(t^j+T)\right).
\end{aligned}
State
and
Control
Running and terminal costs
ODE model
Mixed state and control constraints
+
boundary conditions
Modelling
Ihno Schrot — The Story Behind the Professional — December 16th 2025
State
and
Control
Running and terminal costs
ODE model
FRAMEWORK TO EFFICIENTLY SOLVE PARAMETRIZED OCPS
\newcommand{\ud}{\mathrm{d}}
\begin{aligned}
&\min_{x(\cdot),u(\cdot)} & \int_{t^j}^{t^j+T_\mathrm{hor}} &\Psi\left(x(t),u(t)\right) \ud t +
\Phi\left(x(t^j+T_\mathrm{hor})\right)\\
&\quad\text{s.\,t. }& \dot{x}(t) &= f\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T_\mathrm{hor}],\\
&& x(t^j) &= x^j,&&\\
&& 0 &\leq h\left(x(t),u(t)\right),\quad t\in[t^j,t^j+T_\mathrm{hor}],\\
&& 0 &= r^{\mathrm{e}} \left(x(t^j),x(t^j+T_\mathrm{hor})\right),\\
&& 0 &\leq r^{\mathrm{i}} \left(x(t^j),x(t^j+T_\mathrm{hor})\right).
\end{aligned}
\(\infty\) - dimensional OCP
Modelling
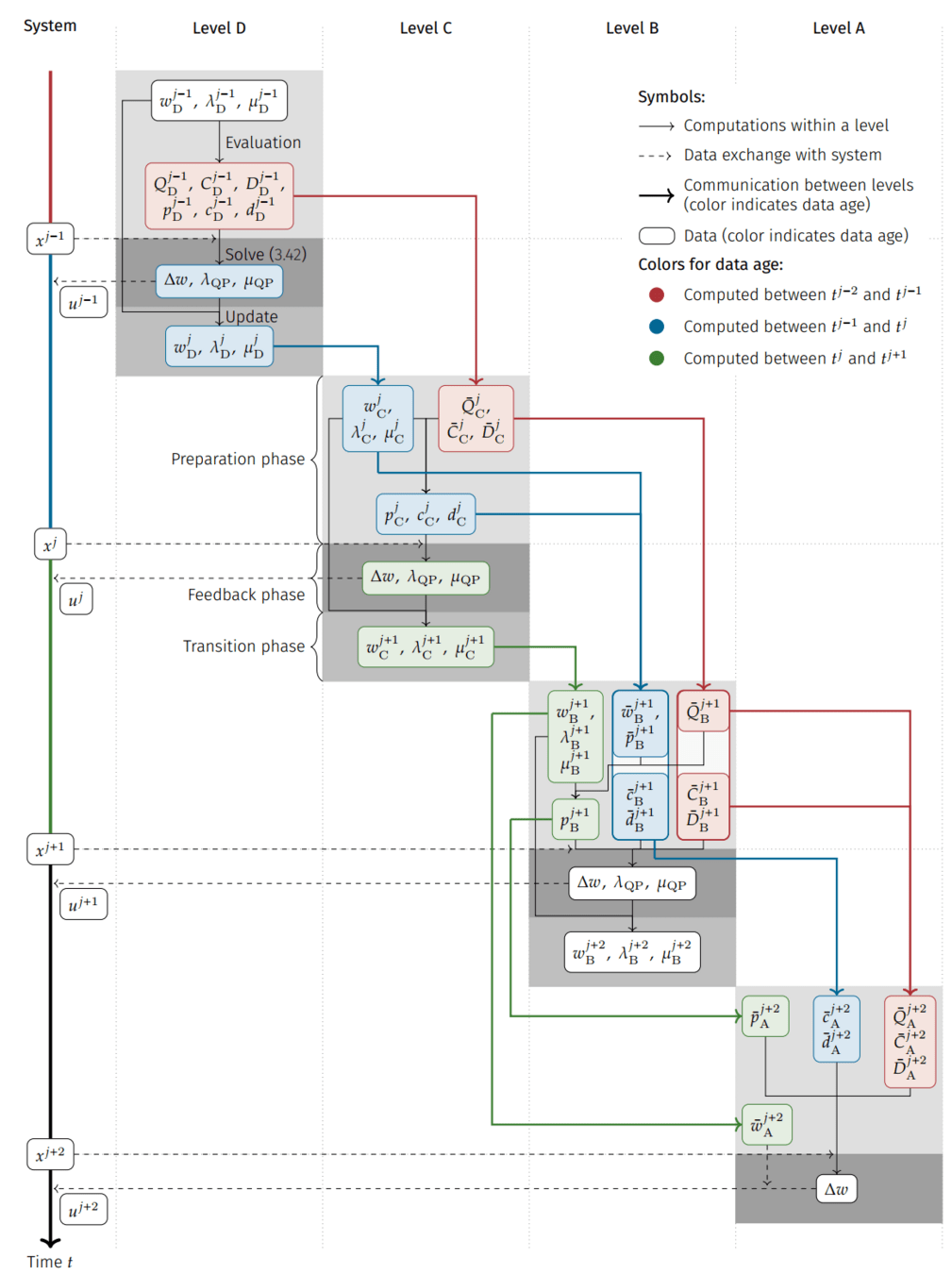
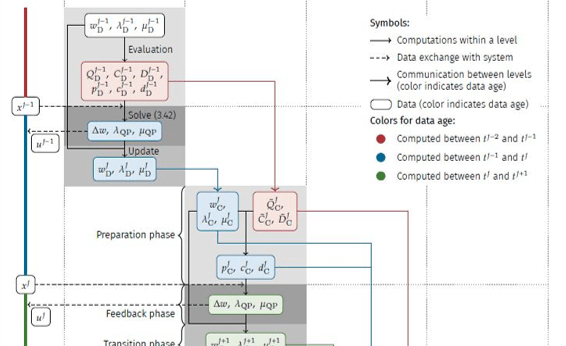
Multi-Level Iterations (MLI)
[Wirsching, 2018]
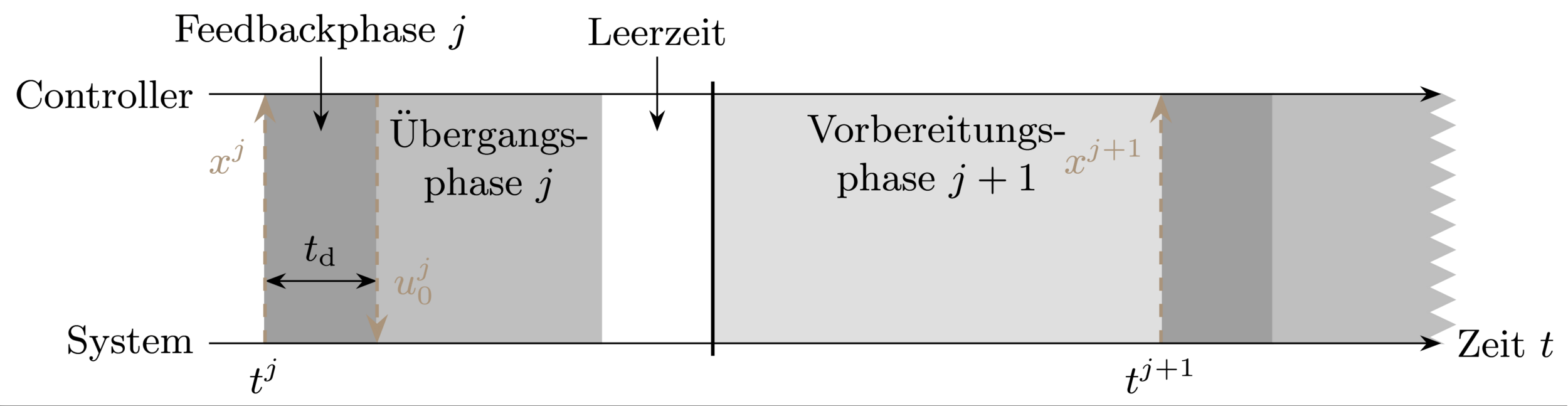
Real-Time Iterations (RTI)
[Diehl et. al, 2002]
\newcommand{\ud}{\mathrm{d}}
\begin{aligned}
&\min_{\substack{s\in\mathbb{R}^{n_s}\\q\in\mathbb{R}^{n_q}}} & \sum_{m=0}^{N-1} &\Psi_m\left(s_m,q_m\right) +
\Phi\left(s_N\right)\\
&\quad\text{s.\,t. }& 0 &= x\left(\tau_{m+1};s_m,q_m\right)-s_{m+1},\quad m=0,\ldots,N-1,\\
&& 0 &= x^j - s_0,&&\\
&& 0 &\leq h\left(s_m,q_m\right),\quad m=0,\ldots,N-1,\\
&& 0 &= r^{\mathrm{e}} \left(s_0,s_N\right),\\
&& 0 &\leq r^{\mathrm{i}} \left(s_0,s_N\right).
\end{aligned}
Nonlinear Program (NLP)
Direct Multiple Shooting (DMS)
[Bock, Plitt 1984]
- [Bock, Plitt, 1984] H. G. Bock and K. J. Plitt. “A Multiple Shooting Algorithm for Direct Solution of Optimal Control Problems”. In: IFAC Proceedings Volumes 17.2 (1984). 9th IFAC World Congress: A Bridge Between Control Science and Technology, Budapest, Hungary, 2-6 July 1984, pp. 1603–1608
- [Diehl et. al., 2002] M. Diehl, H. G. Bock, J. P. Schlöder, R. Findeisen, Z. Nagy, and F. Allgöwer. “Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations”. In: Journal of Process Control 12.4 (2002), pp. 577–585
- [Wirsching, 2018] L. Wirsching. “Multi-level iteration schemes with adaptive level choice for nonlinear model predictive control”. PhD thesis. Heidelberg University, 2018
\newcommand{\ud}{\mathrm{d}}
\begin{aligned}
&\min_{\substack{\Delta s\in\mathbb{R}^{n_s}\\\Delta q\in\mathbb{R}^{n_q}}} & &\frac{1}{2}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}^T\begin{pmatrix}B^{ss} & B^{sq} \\ B^{qs} & B^{qq}\end{pmatrix}\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix} + \begin{pmatrix}b^s\\b^q\end{pmatrix}^T\begin{pmatrix}\Delta s \\ \Delta q\end{pmatrix}\\
&\quad\text{s.\,t. }& 0 &= S_m^s\Delta s_m + S_m^q\Delta q_m - \Delta s_{m+1},\quad m=0,\ldots,M-1,\\
&& 0 &= x^j - s_0 - \Delta s_0,&&\\
&& 0 &\leq H_m^s\Delta s_m + H_m^q\Delta q_m + h_m,\quad m=0,\ldots,M-1,\\
&& 0 &= R_{s_0}^\mathrm{e}\Delta s_0 + R_{s_M}^\mathrm{e}\Delta s_M + r^\mathrm{e},\\
&& 0 &\leq R_{s_0}^\mathrm{i}\Delta s_0 + R_{s_M}^\mathrm{i}\Delta s_M + r^\mathrm{i}.
\end{aligned}
Quadratic Program (QP)
Tailored
SQP-Method
Ihno Schrot — The Story Behind the Professional — December 16th 2025
MULTIPLE SHOOTING DISCRETIZATION
- [Bock, Plitt, 1984] H. G. Bock and K. J. Plitt. “A Multiple Shooting Algorithm for Direct Solution of Optimal Control Problems”. In: IFAC Proceedings Volumes 17.2 (1984). 9th IFAC World Congress: A Bridge Between Control Science and Technology, Budapest, Hungary, 2-6 July 1984, pp. 1603–1608
Ihno Schrot — The Story Behind the Professional — December 16th 2025
-
Introduce Shooting Grid
-
Replace state trajectory by points
-
Replace control trajectory by, e.g., piecewise constant controls
-
Introduce Matching Conditions
- Constraints and objective functions are evaluated only at shooting nodes
Control $$u(\cdot)$$
s_0
s_1
s_2
s_N
q_0
q_1
q_2
q_{N-1}
\underbrace{x(\tau_{i+1};s_i,q_i)} - s_{i+1} = 0
Infinite-Dimensional
\tau_0
\tau_1
\tau_N
State $$x(\cdot)$$
SEQUENTIAL QUADRATIC PROGRAMMING
Ihno Schrot — The Story Behind the Professional — December 16th 2025
\begin{aligned}
&\min_x & & f(x)\\
& ~~\text{s.t.} & & g(x) = 0
\end{aligned}
F(x)=0
Nonlinear System of Equations
SQP Method
Step of Newton's Method
Optimality Conditions
Quadratic Approximation
Quadratic Program
\begin{aligned}
&\min_{\Delta x} & &\frac{1}{2}\Delta x ^T \nabla_{xx}^2\mathcal{L}\left(x_k,\lambda_k\right)\Delta x + \nabla_x f(x_k)^T\Delta x\\
& ~~\text{s.t.} & & g(x_k) + \nabla_x g(x_k)^T \Delta x_k = 0
\end{aligned}
Step $$\Delta x$$
Current Guess $$x_k$$
Solving the QP
Update
FOCUS OF MY THESIS
Ihno Schrot — The Story Behind the Professional — December 16th 2025
Application:
EACC
-
Realistic test problem with
real look-up tables and driving data -
Numerical tests
Stability
of
Inexact NMPC
-
OCP semilinear parabolic PDEs
-
Proof of asymptotic stability
of system-optimizer-dynamics
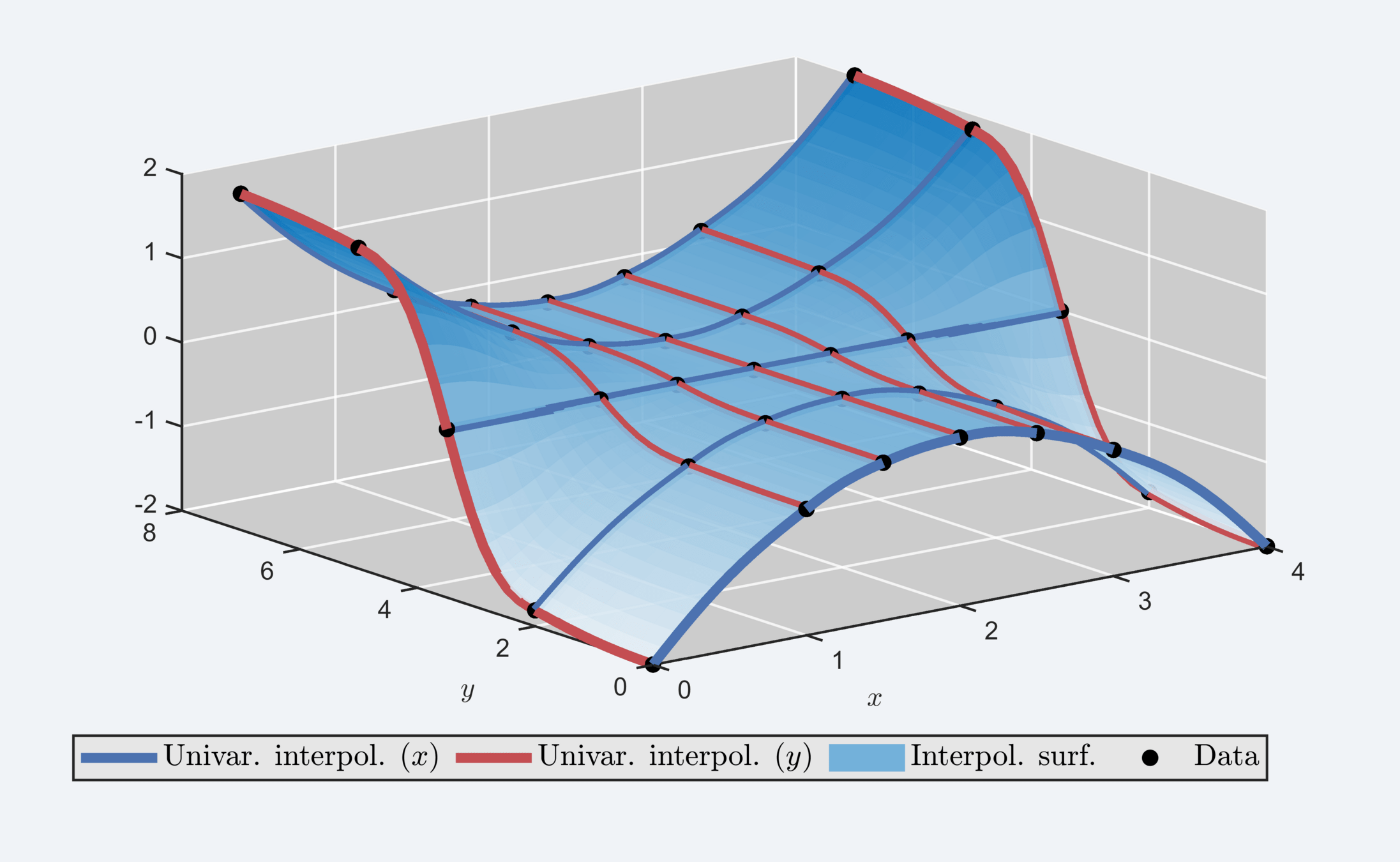
Shape-
Preserving
Interpolation
-
Classification for multivariate case
-
Method for multivariate, shape-preserving, smooth interpolation
Incorporate external inputs in
- DMS
- RTI
- MLI
External
Inputs
-
Scenario-based online feedback
-
Online effort: matrix-vector-product or QP-solve
SensEIS
FEEDBACK
OUTSIDE OF WORK
Mountains
More Sports
Tennis
Ihno Schrot — The Story Behind the Professional — December 16th 2025
The story behind the professional
By Ihno Schrot
