Quantum Computing
Hacking into Nature's Computer
About Presenter James Weaver
Java Champion, JavaOne Rockstar, plays well with others, etc :-)
Author of several Java/JavaFX/RaspPi books
Developer Advocate & International Speaker for Pivotal
Mission: "Transform how the world builds software"
Mission: "Transform how the world builds software"
About Presenter Dr. Johan Vos
Developer / Physicist / Writer / Speaker - Gluon
About Gluon
Gluon CloudLink
Concepts we'll address today
Introduction to quantum computing
Representing qubits
Axioms of quantum mechanics
- Superposition principle
- Measurement
- Unitary evolution
Quantum computing algorithms
Quantum entanglement
More algorithms
Supplementary resources
Intro to Quantum Computing
History repeating itself
massive hardware, limited bits, software infancy
Quantum computers make direct use of quantum-mechanical phenomena, such as superposition and entanglement, to perform operations on data.
Some QC proofs of concept
mini-universe in your garage
Don't try this at home, kids!
Why use a quantum computer?
Feasible on classical computers
Feasible on quantum computers
Solutions to problems
some problems may be solved exponentially faster
Transistors can't get much smaller
the quantum tunneling struggle is real
Breaking RSA crypto
someday maybe, using Shor's algorithm
“If you start factoring 10-digit numbers then it’s going to start getting scary”
Dr. Peter Shor, 2013
Related paper published 25 Jan 1997 by Dr. Shor:
Note: Shor's algorithm was formulated in 1994
Quickly searching unsorted data
using Grover's algorithm
"Programming a quantum computer is particularly interesting since there are multiple things happening in the same hardware simultaneously. One needs to think like both a theoretical physicist and a computer scientist."
Dr. Lov Grover, 2002
Related paper published 17 Jul 1997 by Dr. Grover:
Simulating nature
complex chemical reactions, for example
“Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.”
Dr. Richard Feynman, 1981
Leveraging quantum computing for chemistry
Quantum communication and cryptography
Concepts we'll address today
Introduction to quantum computing
Representing qubits
Axioms of quantum mechanics
- Superposition principle
- Measurement
- Unitary evolution
Quantum computing algorithms
Quantum entanglement
More algorithms
Supplementary resources
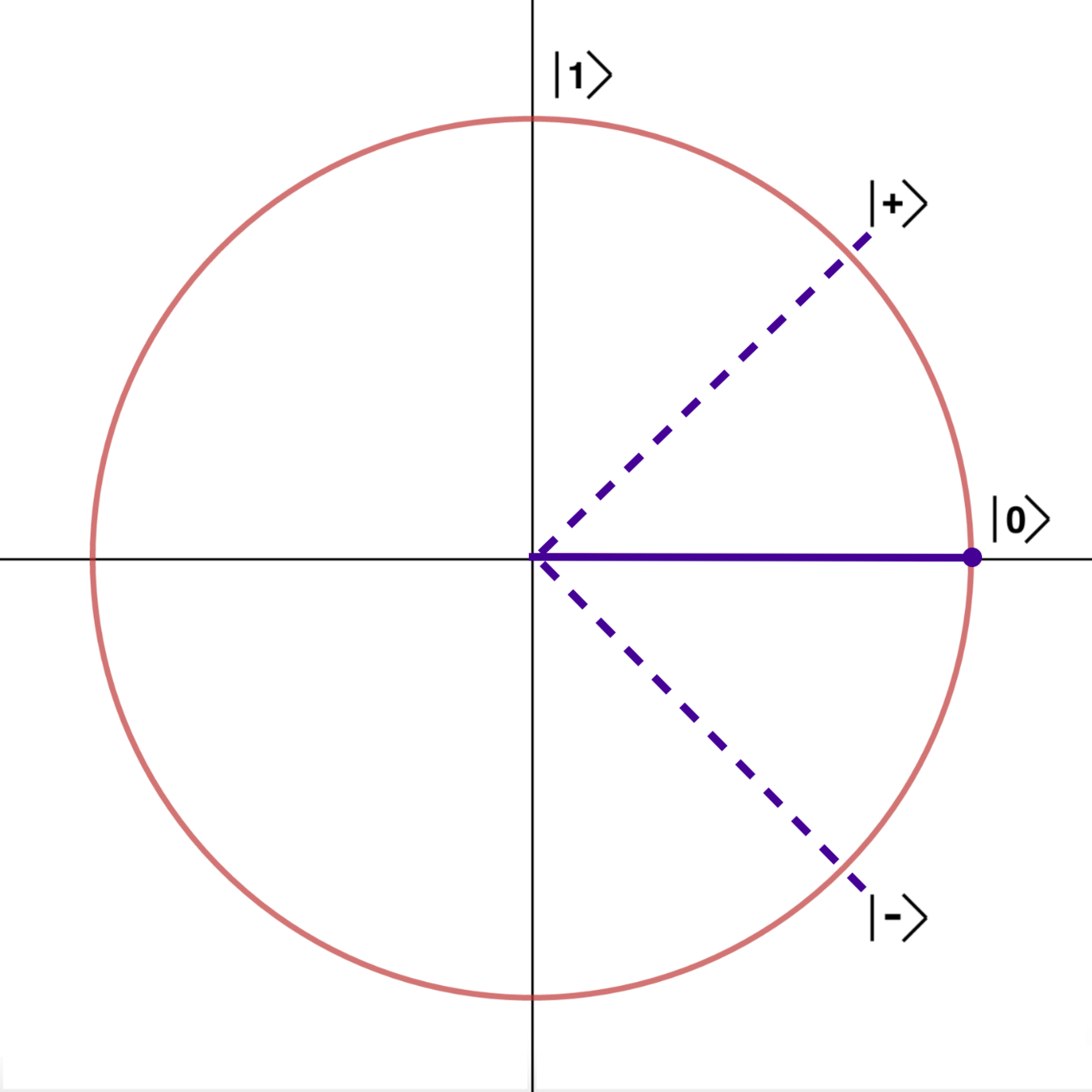
Classical bits vs. qubits
two discrete states vs. infinite superpositions
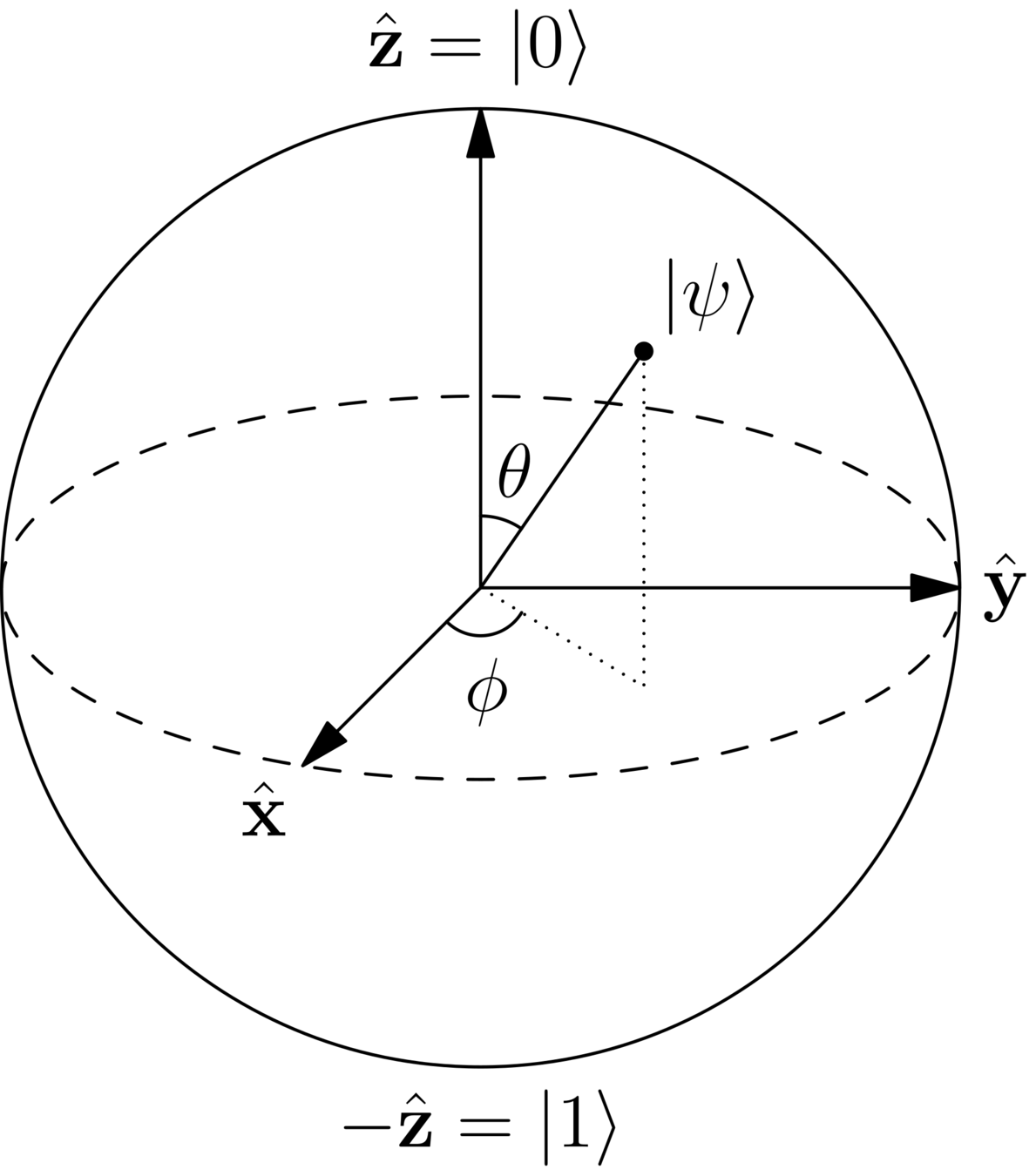
Qubit geometry
Representing qubits
ket notation, vectors, and geometrically
Hardware representation of qubits
| Physical support | Type | ||
|---|---|---|---|
| Photon | Polarization | Horizontal | Vertical |
| Electrons | Spin | Up | Down |
| Superconductor | Charge | Uncharged | Charged |
\vert0\rangle
\vert1\rangle
Superconducting qubits on a chip
Concepts we'll address today
Introduction to quantum computing
Representing qubits
Axioms of quantum mechanics
- Superposition principle
- Measurement
- Unitary evolution
Quantum computing algorithms
Quantum entanglement
More algorithms
Supplementary resources
Diagonally polarized photon
collapsing to a measurement basis state
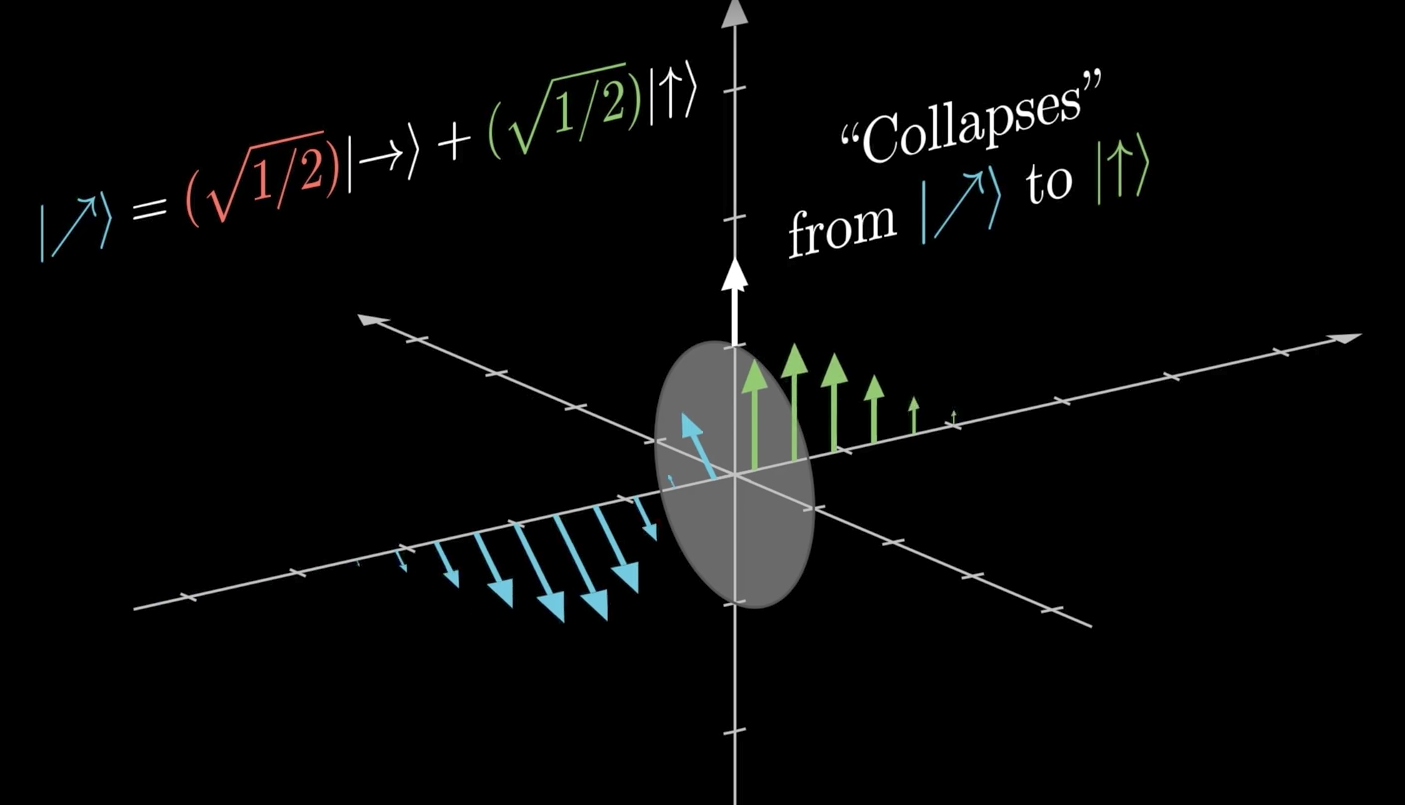
Measuring in the computational basis
Visualizing quantum measurement
Polarized lenses blocking light
Vertically polarized photon
won't pass through horizontally polarized filter
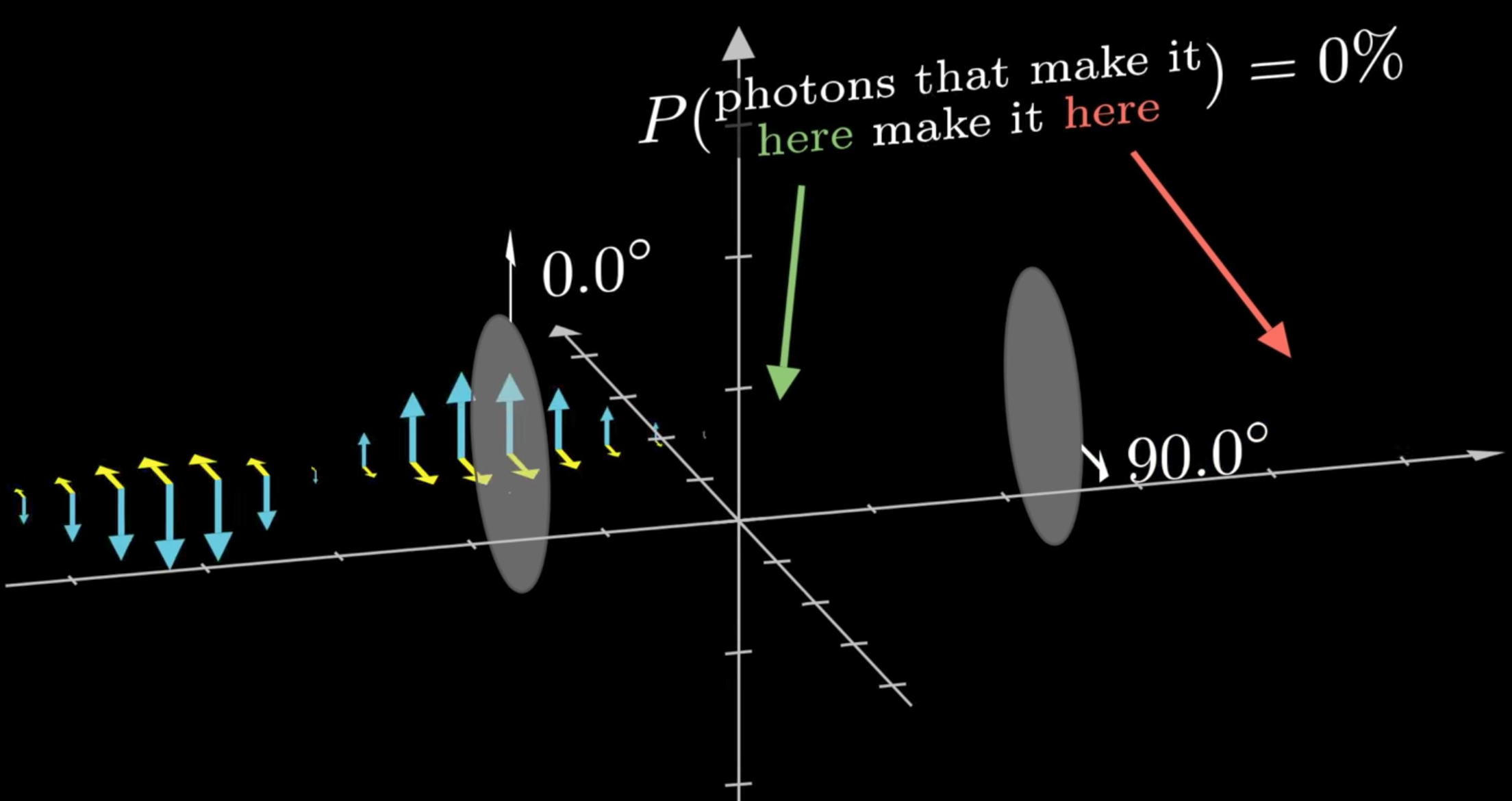
Superposition collapse
Why does adding a lens let more light through?
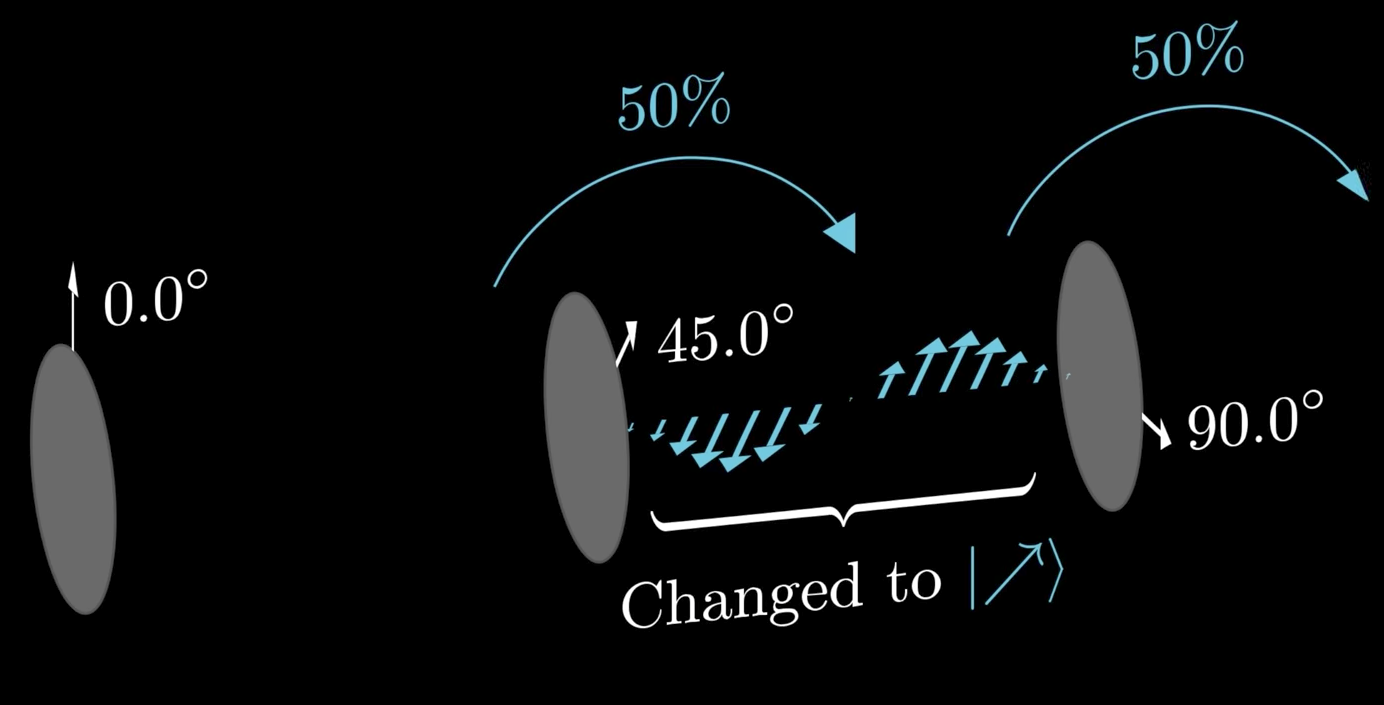
Measuring in an alternative basis
Orchestrating superpositions
Measuring in various basis states
Double-slit experiment
constructive and destructive interference
Text
Classic logic gates
a quick review for comparison to quantum gates
Some quantum gates
matrix operations model quantum mechanical behavior
More quantum gates
just going though a phase
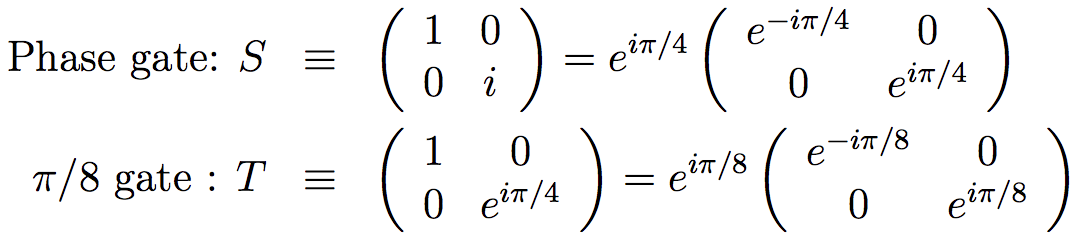
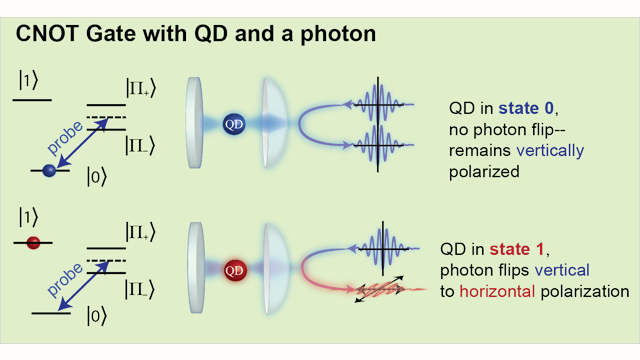
Quantum gate hardware
example using photons
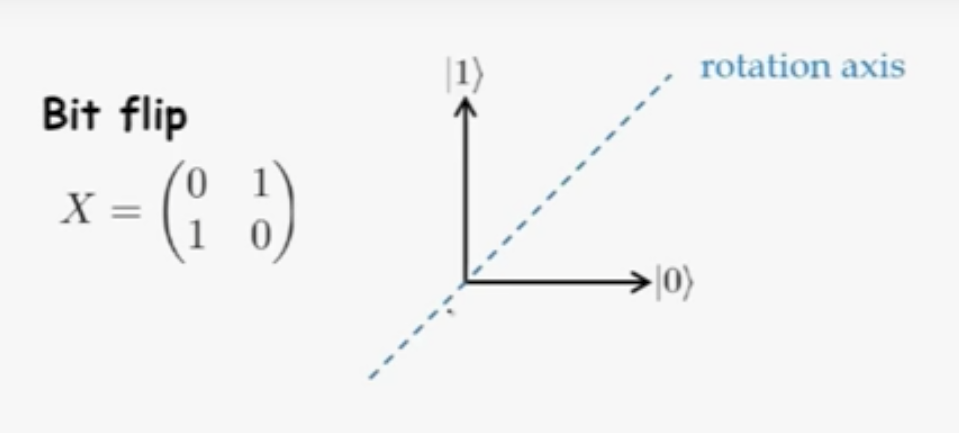
NOT / Pauli-X / Bit flip gate
from video: Single qubit gates - Umesh Vazirani
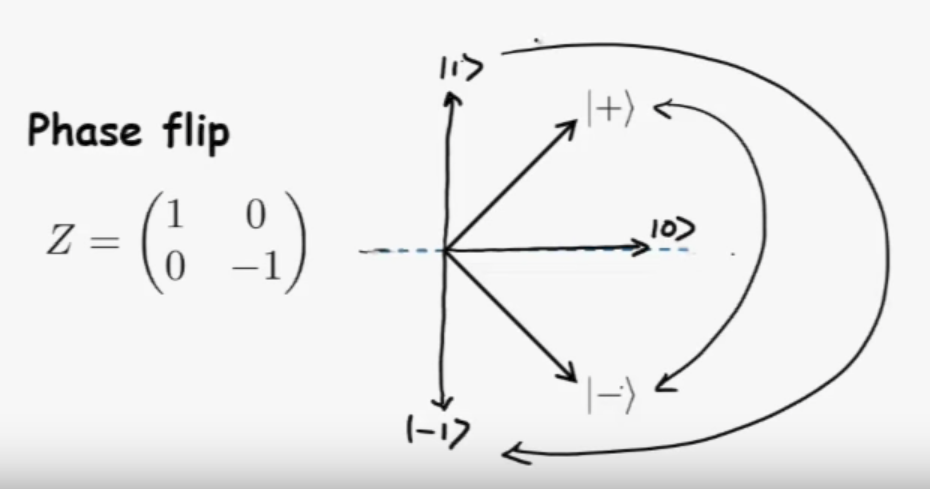
Pauli-Z / Phase flip gate
from video: Single qubit gates - Umesh Vazirani
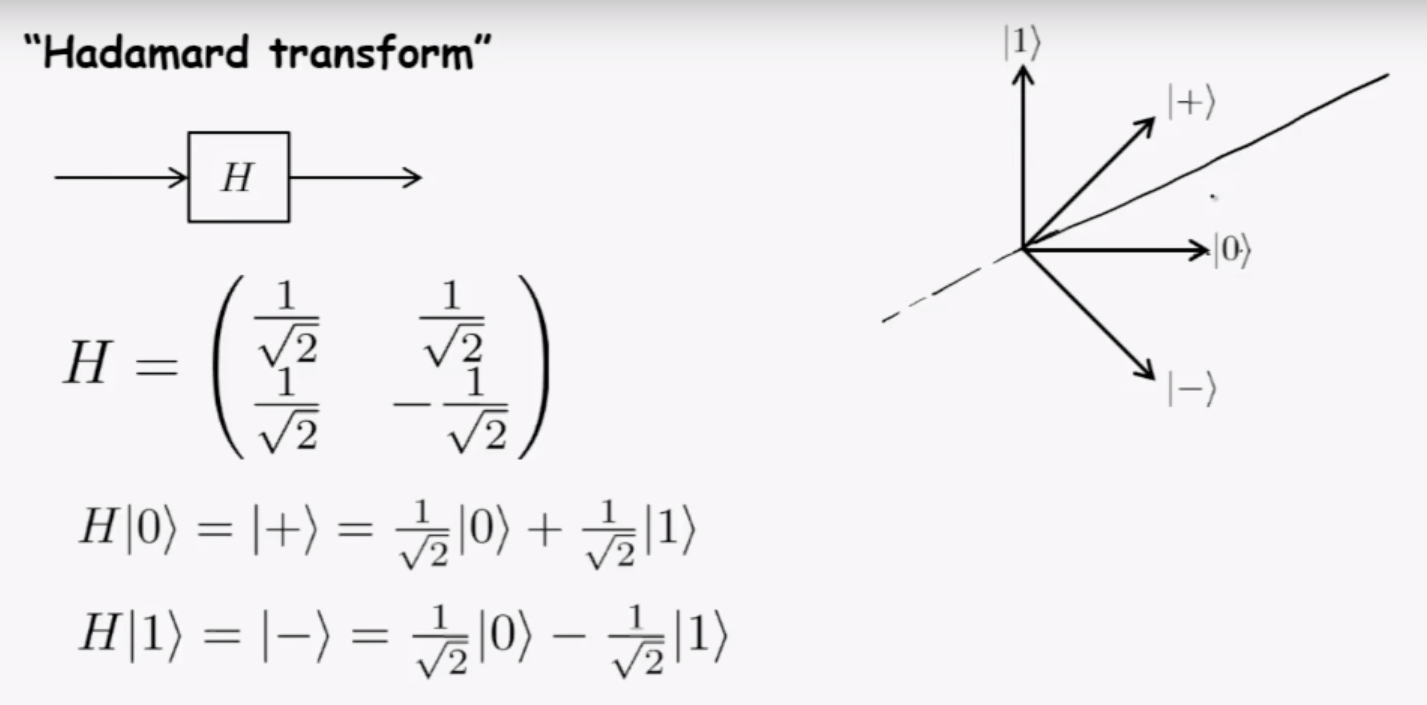
Hadamard gate
from video: Single qubit gates - Umesh Vazirani
CNOT gate
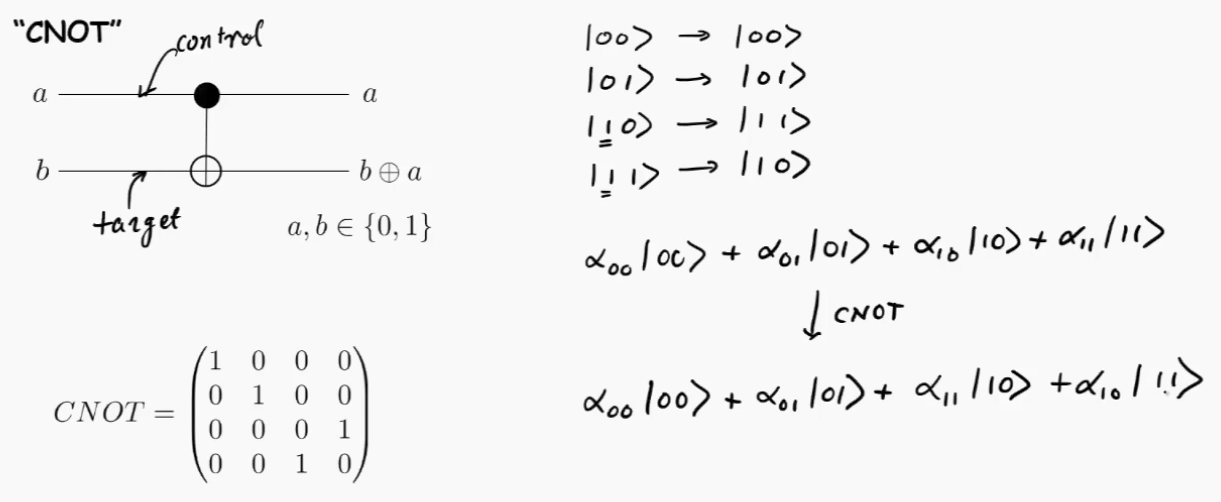
Strange?
Java-based quantum simulator
Exploring the quantum simulator
e.g. visualize states of multiple qubits: |00>
Exploring the quantum simulator
e.g. visualize states of multiple qubits: |01>
Simple quantum circuit
collapses to 8 random states with equal probability
Quantum superpositions
and observability
Measuring qubits
collapses to a basis state, discarding superposition
Measuring quantum state
a Java analogy
from an IndicThreads slide deck
Measuring quantum state
Hitchhiker's Guide to the Galaxy analogy
Deep Thought after 7.5 million years of calculation
Concepts we'll address today
Introduction to quantum computing
Representing qubits
Axioms of quantum mechanics
- Superposition principle
- Measurement
- Unitary evolution
Quantum computing algorithms
Quantum entanglement
More algorithms
Supplementary resources
Deutsch's algorithm (1985)
Literally the Hello World of quantum algorithms
Deutsch's algorithm
Determine if function is constant or balanced
| Input a | Constant f(a) | Constant f(a) | Balanced f(a) | Balanced f(a) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
Deutsch's algorithm
How many queries of the oracle to solve?
Classical:
This oracle requires 2 queries classically
Quantum:
We create a superposition of inputs to the oracle for constructive/destructive interference.
1
2
Querying the oracle classically
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
0 \\
1 \\
0 \\
0
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
1
\end{bmatrix}
\vert01\rangle
\vert11\rangle
example: f (0) = 0 and f (1) = 1 balanced
Quantum parallelism
what is it, really?
Double-slit experiment
constructive and destructive interference
Text
Choreographing interference
to increase the chance of getting the right answer
Text
Excerpts from “THE TALK” by Scott Aaronson and Zach Weinersmith
Querying the oracle quantumly
\begin{bmatrix}
+\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} \\
+\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} \\
+\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\
+\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2}
\end{bmatrix}
\cdot
\begin{bmatrix}
0 \\
0 \\
1 \\
0
\end{bmatrix}
=
\begin{bmatrix}
+\frac{1}{2} \\
+\frac{1}{2} \\
-\frac{1}{2} \\
-\frac{1}{2}
\end{bmatrix}
example: f (0) = 0 and f (1) = 1 balanced
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
+\frac{1}{2} \\
+\frac{1}{2} \\
-\frac{1}{2} \\
-\frac{1}{2}
\end{bmatrix}
=
\begin{bmatrix}
+\frac{1}{2} \\
-\frac{1}{2} \\
-\frac{1}{2} \\
+\frac{1}{2}
\end{bmatrix}
\begin{bmatrix}
+\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} & +\frac{1}{2} \\
+\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} \\
+\frac{1}{2} & +\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\
+\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & +\frac{1}{2}
\end{bmatrix}
\cdot
\begin{bmatrix}
+\frac{1}{2} \\
-\frac{1}{2} \\
-\frac{1}{2} \\
+\frac{1}{2}
\end{bmatrix}
=
\begin{bmatrix}
0 \\
0 \\
0 \\
1
\end{bmatrix}
Lecture 3: One Qubit, Two Qubit by Dave Bacon, University of Washington (Deutsch slightly modified)
=
\begin{bmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{bmatrix}
Deutsch (slightly modified)
Why constant vs. balance require only one query
| Inp | Con |
|---|---|
| 0 | 0 |
| 1 | 0 |
| Inp | Con |
|---|---|
| 0 | 1 |
| 1 | 1 |
| Inp | Bal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| Inp | Bal |
|---|---|
| 0 | 1 |
| 1 | 0 |
Deutsch's algorithm
with oracle having constant function
Leverages phase-kickback from the bottom wire to choreograph constructive and destructive interference
Expected result is 100% probability of measuring
\vert0\rangle
Deutsch's algorithm
with oracle having balanced function
Expected result is 0% probability of measuring
\vert0\rangle
Leverages phase-kickback from the bottom wire to choreograph constructive and destructive interference
Deutsch-Jozsa algorithm
exponentially faster than classical
Deutsch-Jozsa algorithm, 1992
Determine if function is constant or balanced
| Input | Constant | Constant | Balanced | Balanced |
|---|---|---|---|---|
| 000 | 0 | 1 | 0 | 1 |
| 001 | 0 | 1 | 1 | 0 |
| 010 | 0 | 1 | 0 | 1 |
| 011 | 0 | 1 | 1 | 0 |
| 100 | 0 | 1 | 0 | 1 |
| 101 | 0 | 1 | 1 | 0 |
| 110 | 0 | 1 | 0 | 1 |
| 111 | 0 | 1 | 1 | 0 |
Results when querying our example oracle
Deutsch-Jozsa algorithm
How many invocations of the oracle to solve?
Classical:
Our oracle (black box) requires 5 invocations classically
Quantum:
We create a superposition of inputs to the oracle, and use the phase-kickback trick, for constructive/destructive interference. See:
see also: Wikipedia Deutsch-Jozsa Decoherence section
2^{(n-1)}+1
1
(Exponentially faster!)
Deutsch-Jozsa algorithm
with oracle having constant function
Deutsch-Jozsa algorithm
example oracle with constant function
Deutsch-Jozsa algorithm
with oracle having balanced function
Deutsch-Jozsa algorithm
example oracle with balanced function
Deutsch-Jozsa implemented in Quil
Deutsch-Jozsa implemented in Quil
Concepts we'll address today
Introduction to quantum computing
Representing qubits
Axioms of quantum mechanics
- Superposition principle
- Measurement
- Unitary evolution
Quantum computing algorithms
Quantum entanglement
More algorithms
Supplementary resources
Quantum entanglement
Alice and Bob's long running relationship
Quantum entanglement
basic circuit
Quantum teleportation
and the no cloning theorem
Superdense coding
example circuit
Bell inequality test
(CHSH game)
Concepts we'll address today
Introduction to quantum computing
Representing qubits
Axioms of quantum mechanics
- Superposition principle
- Measurement
- Unitary evolution
Quantum computing algorithms
Quantum entanglement
More algorithms
Supplementary resources
Bernstein-Vazirani algorithm
basic circuit
Simon's algorithm
the quantum portion
Shor's algorithm
Period finding
using Quantum Fourier Transform
Grover's search
finding a needle in a haystack
Concepts we'll address today
Introduction to quantum computing
Representing qubits
Axioms of quantum mechanics
- Superposition principle
- Measurement
- Unitary evolution
Quantum computing algorithms
Quantum entanglement
More algorithms
Supplementary resources
Complex numbers
aren't complicated
Complex numbers encode
amplitude and phase
Roots of unity
are useful for Shor
Matrices
think two-dimensional arrays
Vector spaces
a home for vectors and scalars
Quantum Computing
Quantum Computing Exposed: Deep Dive
By javafxpert
Quantum Computing Exposed: Deep Dive
Helping developers get started with quantum computing
