What's in your Prior?

Jeremias Sulam

Learned Proximal Networks for Inverse Problems

BIRS Casa Matemática Oaxaca

Computational Harmonic Analysis in Data Science and Machine Learning

"The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. [...] Seeking an improvement that makes a difference in the shorter term, researchers seek to leverage their human knowledge of the domain, but the only thing that matters in the long run is the leveraging of computation. [...]
We want AI agents that can discover like we can, not which contain what we have discovered."

The Bitter Lesson, Rich Sutton 2019

"The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. [...] Seeking an improvement that makes a difference in the shorter term, researchers seek to leverage their human knowledge of the domain, but the only thing that matters in the long run is the leveraging of computation. [...]
We want AI agents that can discover like we can, not which contain what we have discovered."

The Bitter Lesson, Rich Sutton 2019

Inverse Problems

y = A x^* + v

measurements

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

reconstruction

Inverse Problems

y = A x^* + v

measurements

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

reconstruction

= \arg\min_x ~-\log p(y|x) - \log p(x)

= \arg\max_x~ p(x|y)

\text{MAP estimate when }R(x) \propto -~p_x(x):\text{ prior}

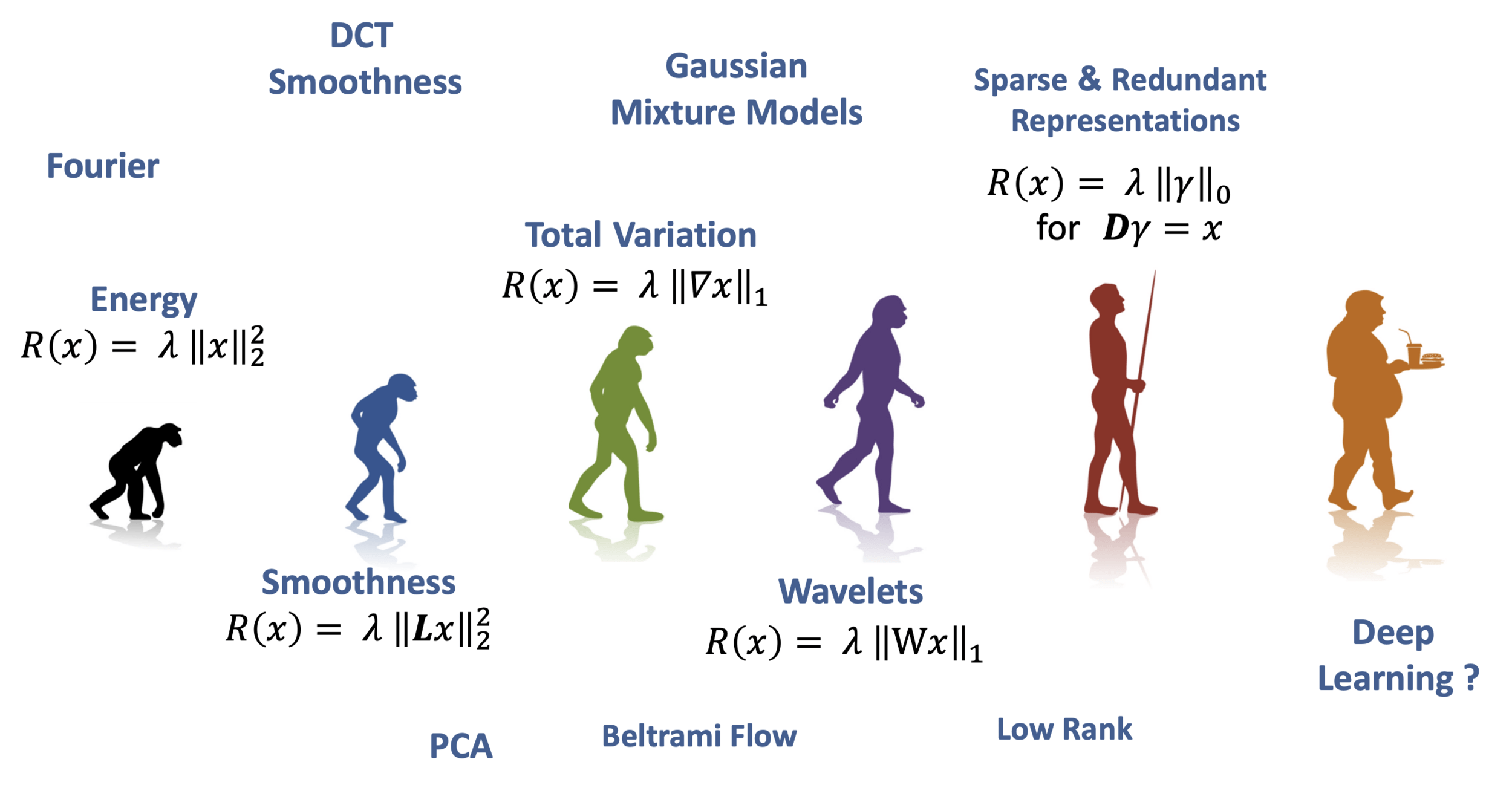
Image Priors

Deep Learning in Inverse Problems

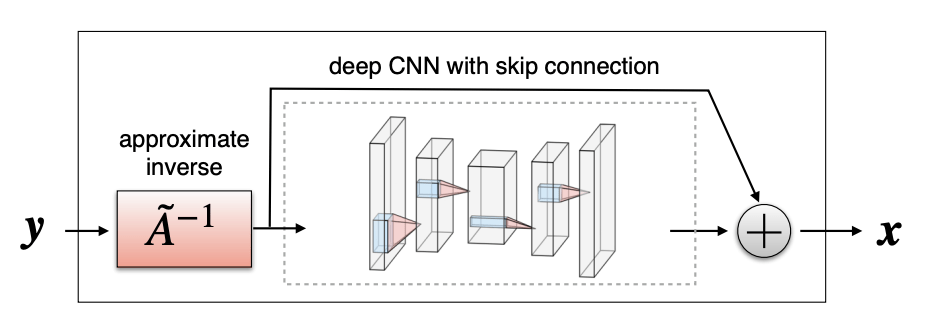
Option A: One-shot methods

Given enough training pairs \({(x_i,y_i)}\) train a network

\(f_\theta(y) = g_\theta(A^+y) \approx x\)

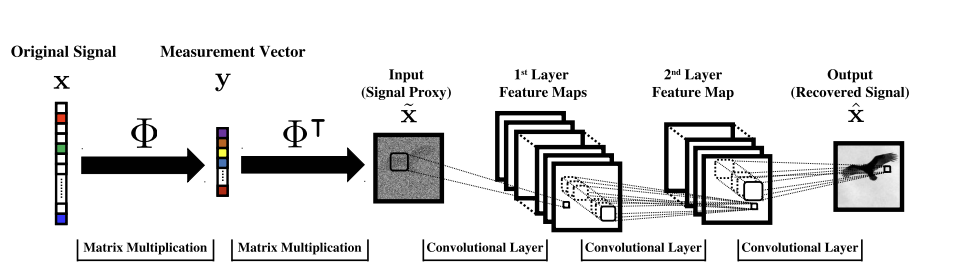
[Mousavi & Baraniuk, 2017]

[Ongie, Willet, et al, 2020]

Deep Learning in Inverse Problems

Option B: data-driven regularizer

Priors as critics

[Lunz, Öktem, Schönlieb, 2020] and others ..

\displaystyle \hat R_\theta(x) = \arg\min_{R_\theta\in \mathcal H} ~ \mathbb E_{x\sim p_x}[R(x)] - \mathbb E_{x\sim q }[R(x)]

via MLE
```
[Ye Tan, ..., Schönlieb, 2024], ...
```

RED
```
[Romano et al, 2017] ...
```

Generative Models
```
[Bora et al, 2017] ...
```

\displaystyle \hat R_\theta(x) = \mathbb 1_{[\exist z : G(z)=x]}

\[\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \]

\[\hat R_\theta(x)\]

Deep Learning in Inverse Problems

Option C: Implicit Priors (via Plug&Play)

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

Proximal Gradient Descent: \( x^{t+1} = \text{prox}_R \left(x^t - \eta A^T(Ax^t-y)\right) \)

\text{prox}_R \left( u \right) = \arg\min_x \frac 12 \|u - x\|_2^2 + R(x)

\text{prox}_R \left( u \right) = \texttt{MAP}(x|u), \qquad \text{when } u = x + v, ~ v\sim\mathcal N(0,I\sigma^2)

... a denoiser

Deep Learning in Inverse Problems

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)

any latest and greatest NN denoiser

[Venkatakrishnan et al., 2013; Zhang et al., 2017b; Meinhardt et al., 2017; Zhang et al., 2021; Kamilov et al., 2023b; Terris et al., 2023]

[Gilton, Ongie, Willett, 2019]

Proximal Gradient Descent: \( x^{t+1} = {\color{red}f_\theta} \left(x^t - \eta A^T(A(x^t)-y)\right) \)

Option C: Implicit Priors

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ? and for what \(R(x)\)?

Deep Learning in Inverse Problems

\(\mathcal H_\text{prox} = \{f = \text{prox}_R\}\)

\(\mathcal H = \{f: \mathbb R^n \to \mathbb R^n\}\)

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ? and for what \(R(x)\)?

Question 2)

Can we estimate the "correct" prox?

Deep Learning in Inverse Problems

\(\mathcal H = \{f: \mathbb R^n \to \mathbb R^n\}\)

\(\mathcal H_\text{prox} = \{f = \text{prox}_R\}\)

\text{prox}_R : R(x) = -\log p_x(x)

\(\mathcal H = \{f: \mathbb R^n \to \mathbb R^n\}\)

Interpretable Inverse Problems

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ?

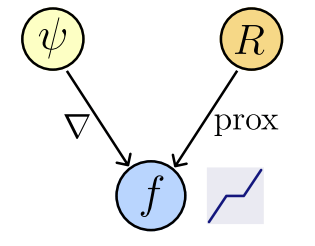
Theorem [Gribonval & Nikolova, 2020]

\( f(x) \in \text{prox}_R(x) ~\Leftrightarrow \exist ~ \text{convex l.s.c.}~ \psi: \mathbb R^n\to\mathbb R : f(x) \in \partial \psi(x)~\)

Interpretable Inverse Problems

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ?

\(R(x)\) need not be convex

Learned Proximal Networks

Take \(f_\theta(x) = \nabla \psi_\theta(x)\) for convex (and differentiable) \(\psi_\theta\)

\( f(x) \in \text{prox}_R(x) ~\Leftrightarrow \exist ~ \text{convex l.s.c.}~ \psi: \mathbb R^n\to\mathbb R : f(x) \in \partial \psi(x)~\)

Theorem [Gribonval & Nikolova, 2020]

Interpretable Inverse Problems

Question 1)

When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ?

\(R(x)\) need not be convex

Learned Proximal Networks

Take \(f_\theta(x) = \nabla \psi_\theta(x)\) for convex (and differentiable) \(\psi_\theta\)

\( f(x) \in \text{prox}_R(x) ~\Leftrightarrow \exist ~ \text{convex l.s.c.}~ \psi: \mathbb R^n\to\mathbb R : f(x) \in \partial \psi(x)~\)

Theorem [Gribonval & Nikolova, 2020]

\psi_\theta : \mathbb R^d \to \mathbb R \text{ given by } \psi_\theta(y) = w^Tz_K + b \text{ and }

z_1 = g(H_1y+b_1), \quad z_k = g(W_k z_{k-1} + H_ky + b_k ), k\in [2,K]

g: \text{convex, non-decreasing, } W_k \text{ and }w_K: \text{non-negative entries}.

\left( \psi_\theta(x,\alpha) = \psi_\theta(x) + \frac \alpha 2 \|x\|^2_2 \right)

Interpretable Inverse Problems

If so, can you know for what \(R(x)\)?

Yes

R_\theta(x) = \langle {\color{red}\hat{f}^{-1}_\theta(x)},x\rangle - \frac 12 \|x\|^2_2 - \psi_\theta( {\color{red}\hat{f}^{-1}_\theta(x)} )

[Gibonval & Nikolova]

Easy! \[{\color{grey}y^* =} \arg\min_{y} \psi(y) - \langle y,x\rangle {\color{grey}= \hat{f}_\theta^{-1}(x)}\]

Interpretable Inverse Problems

Question 2)

(we don't know \(p_x\)!)

\text{Let } y = x+v , \quad ~ x\sim p_x, ~~v \sim \mathcal N(0,\sigma^2I)

f_\theta = \arg\min_{f_\theta:\text{prox}} \mathbb E_{x,y} \left[ {\ell (f_\theta(y),x)} \right]

\bullet ~~ {\ell (f_\theta(y),x)} = \|f_\theta(y) - x\|^2_2 ~~\implies~~ \mathbb E[x|y] \text{ (MMSE)}

\bullet ~~ {\ell (f_\theta(y),x)} = \|f_\theta(y) - x\|_1 ~~\implies~~ \texttt{median}(p_{x|y})

Can we have the "right" prox?
\(f_\theta(y) = \text{prox}_R(y) = \texttt{MAP}(x|y)\)

Could we have \(R(x) = -\log p_x(x)\)?

A learning approach:

What loss function?

Interpretable Inverse Problems

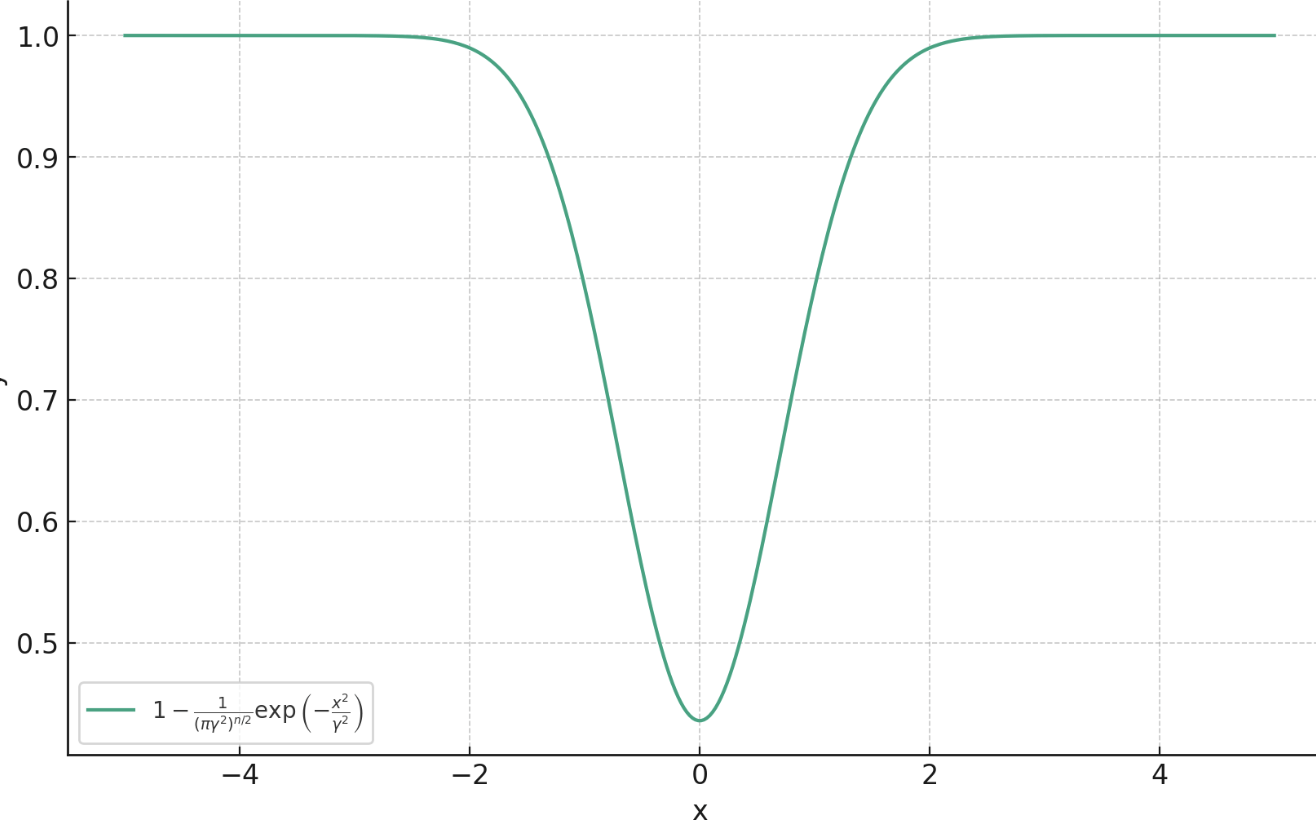
Theorem (informal)

\hat{f}^* = \arg\min_{f} \lim_{\gamma \searrow 0}~ \mathbb E_{x,y} \left[ \ell^\gamma_\text{PM}(f_\theta(y),x)\right]

\hat{f}^*(y) = \arg\max_c p_{x|y}(c) = \text{prox}_{-\sigma^2\log p_x}(y)

\ell^\gamma_\text{PM} (f_\theta(y),x) = 1- \frac{1}{(\pi\gamma^2)^{n/2}} \exp\left( -\frac{\|f(y)-x\|_2^2}{\gamma} \right)

Proximal Matching Loss

\(\gamma\)

Question 2)

Can we have the "right" prox?
\(f_\theta(y) = \text{prox}_R(y) = \texttt{MAP}(x|y)\)

Could we have \(R(x) = -\log p_x(x)\)?

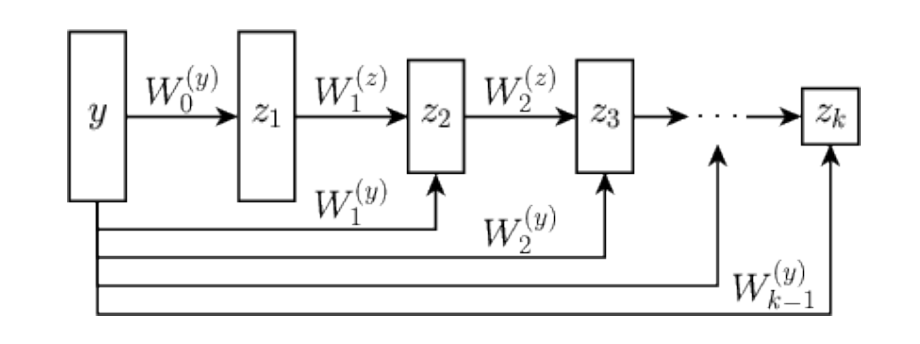
Learned Proximal Networks

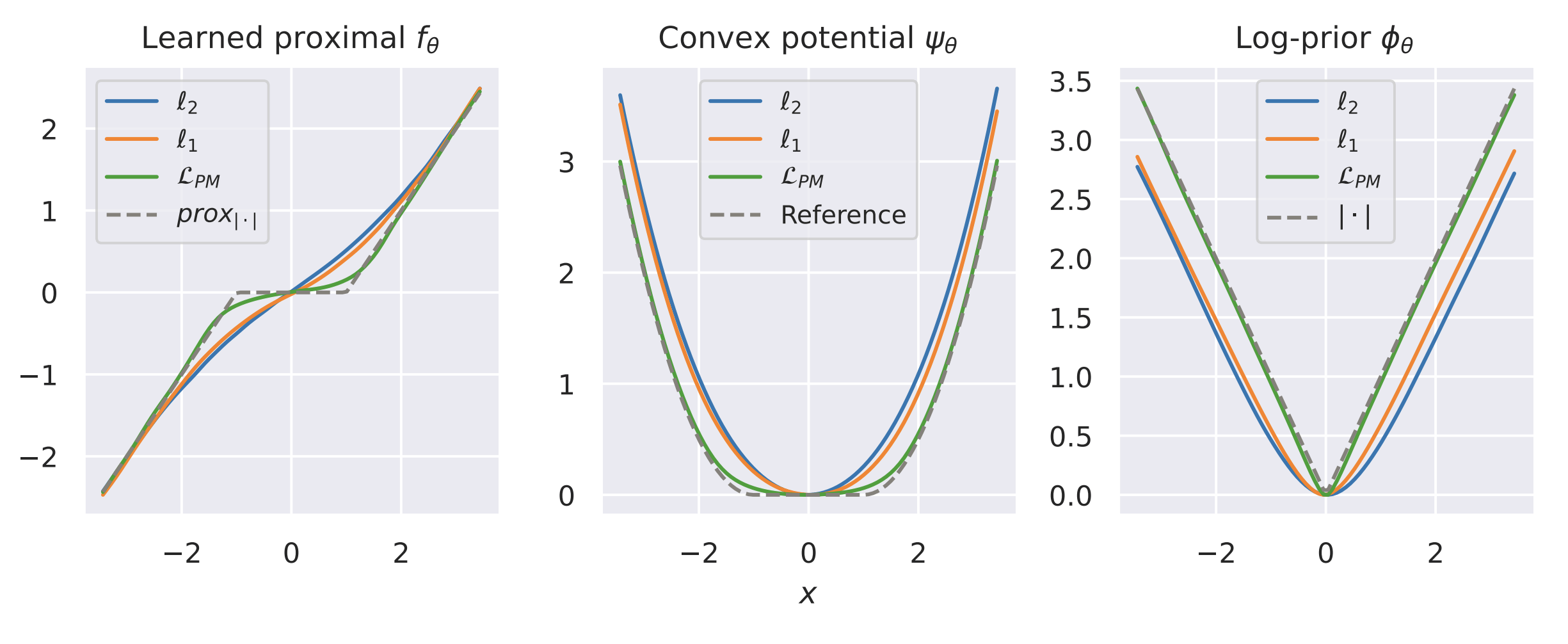
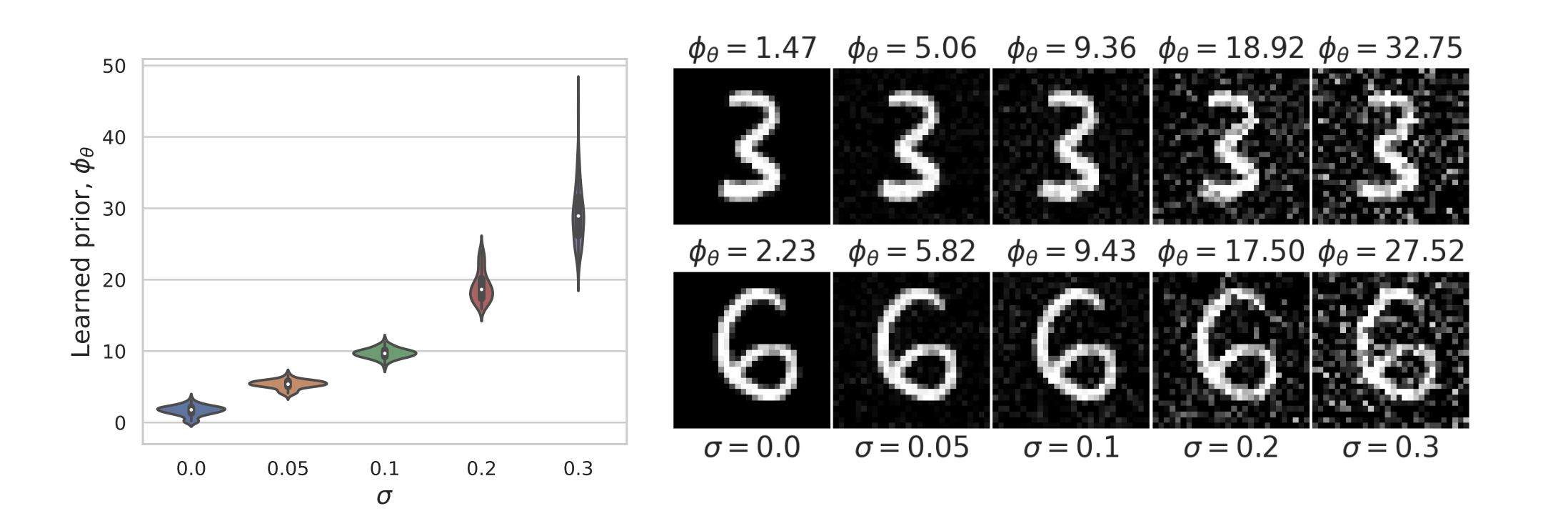
\text{Sample } y = x+v,~ \text{ with } x \sim \text{Laplace}(0,1) \text{ and } v \sim \mathcal N(0,\sigma^2)

Learned Proximal Networks

Learned Proximal Networks

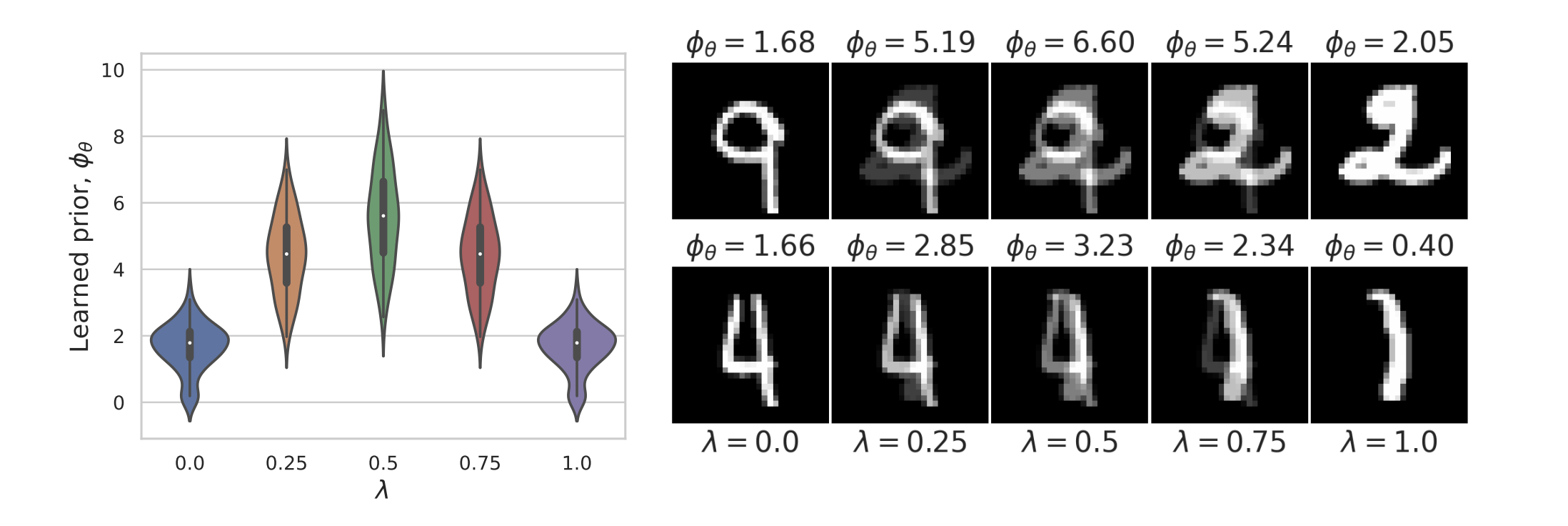
\(R(\tilde{x})\)

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)

Learned Proximal Networks

Convergence guarantees for PnP

x^{t+1} = f_\theta \left(x^t - \eta A^T(Ax^t - y)\right)

[Sreehari et al., 2016; Sun et al., 2019; Chan, 2019; Teodoro et al., 2019]
Convergence of PnP for non-expansive denoisers.
[Ryu et al, 2019]
Convergence for close to contractive operators
[Xu et al, 2020]
Convergence of Plug-and-Play priors with MMSE denoisers
[Hurault et al., 2022]
Lipschitz-bounded denoisers

Theorem (PGD with Learned Proximal Networks)

x^{t+1} = \text{prox}_{\hat R} \left(x^t - \eta A^T(Ax^t - y)\right)

\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)

Let \(f_\theta = \text{prox}_{\hat{R}} {\color{grey}\text{ with } \alpha>0}, \text{ and } 0<\eta<1/\sigma_{\max}(A) \) with smooth activations

\text{Then } \exists x^* : \lim_{k\to\infty} x^t = x^* \text{ and }

f_\theta(x^* - \eta A^T(Ax^*-y)) = x^*

(Analogous results hold for ADMM)

Learned Proximal Networks

Convergence guarantees for PnP

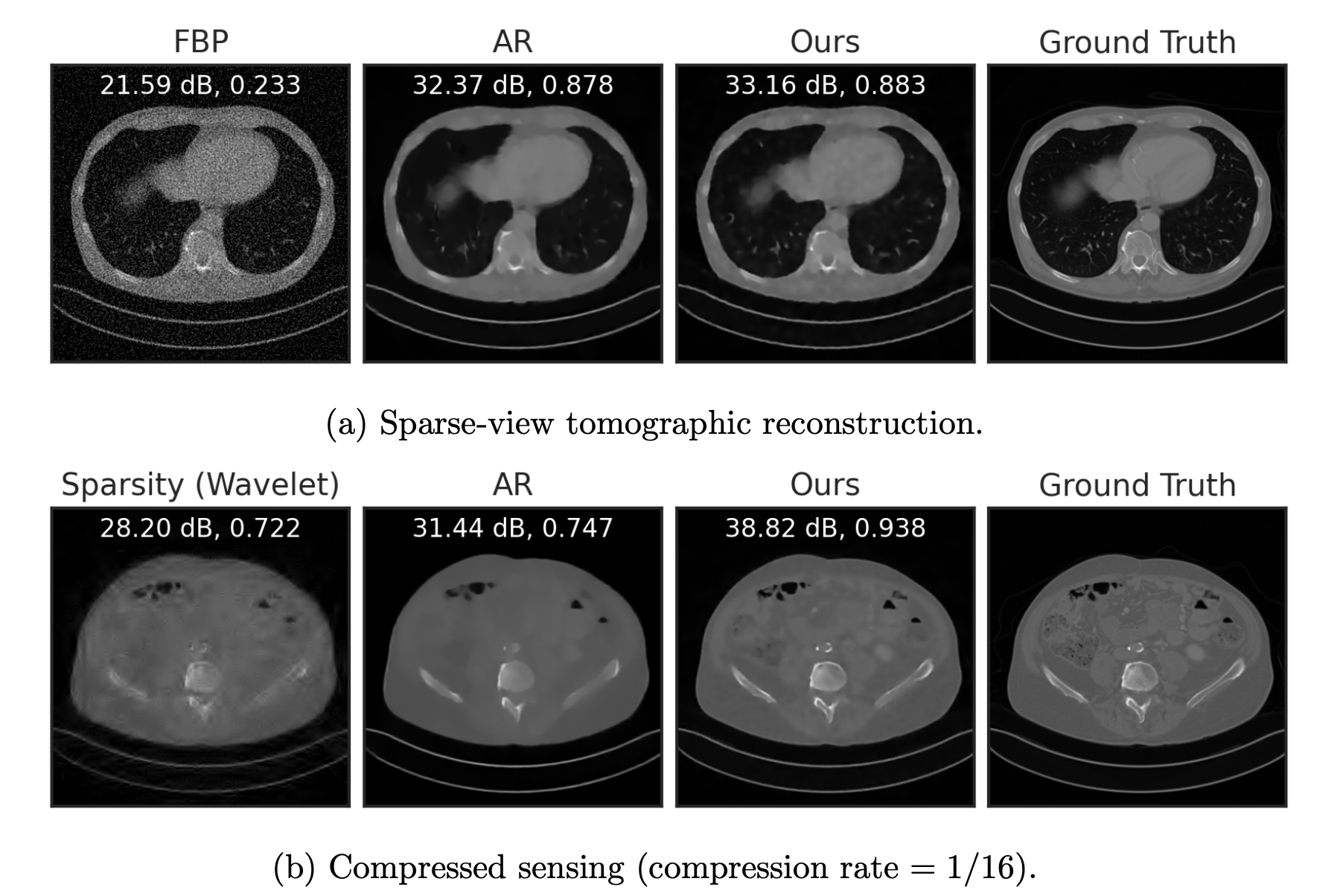
Fang, Buchanan & S. What's in a Prior? Learned Proximal Networks for Inverse Problems. ICLR 2024.

Learned Proximal Networks

Learned proximal networks provide exact proximals for learned regularizers
Framework for general inverse problems and learned priors
Exciting open problems to provide guarantees for "black box" models with minimal guarantees