How I learned to stop worrying and love the Gaussian Process

Jeriek Van den Abeele

Higgs&DM Meeting

Oslo – March 20, 2020

Correlation length-scale

Gaussian process prediction with uncertainty

Estimate from data! (kernels)

Global fits and the need for speed

Idea: consistent comparison of theories to all available data

• High-dimensional parameter space with varying phenomenology                (e.g. MSSM-24)
• Quick prediction of next-to-leading order cross sections is crucial!
• Existing tools have drawbacks   (Prospino: slow, NLL-fast: limited validity)

\(\mathcal{L} = \mathcal{L}_\mathsf{collider} \times  \mathcal{L}_\mathsf{Higgs} \times  \mathcal{L}_\mathsf{DM} \times  \mathcal{L}_\mathsf{EWPO} \times  \mathcal{L}_\mathsf{flavour} \times \ldots\)

Global fits and the need for speed

Idea: consistent comparison of theories to all available data

• High-dimensional parameter space with varying phenomenology                (e.g. MSSM-24)
• Quick prediction of next-to-leading order cross sections is crucial!
• Existing tools have drawbacks   (Prospino: slow, NLL-fast: limited validity)

\(\mathcal{L} = \mathcal{L}_\mathsf{collider} \times  \mathcal{L}_\mathsf{Higgs} \times  \mathcal{L}_\mathsf{DM} \times  \mathcal{L}_\mathsf{EWPO} \times  \mathcal{L}_\mathsf{flavour} \times \ldots\)

[GAMBIT, 1705.07919]

Goal

$$ pp\to\tilde g \tilde g,\ \tilde g \tilde q_i,\ \tilde q_i \tilde q_j, $$

$$\tilde q_i \tilde q_j^{*},\ \tilde b_i \tilde b_i^{*},\ \tilde t_i \tilde t_i^{*}$$

Interface

Method

Pre-trained, distributed Gaussian processes

Stand-alone Python code, also implemented in GAMBIT

Processes

Soon public on GitHub!

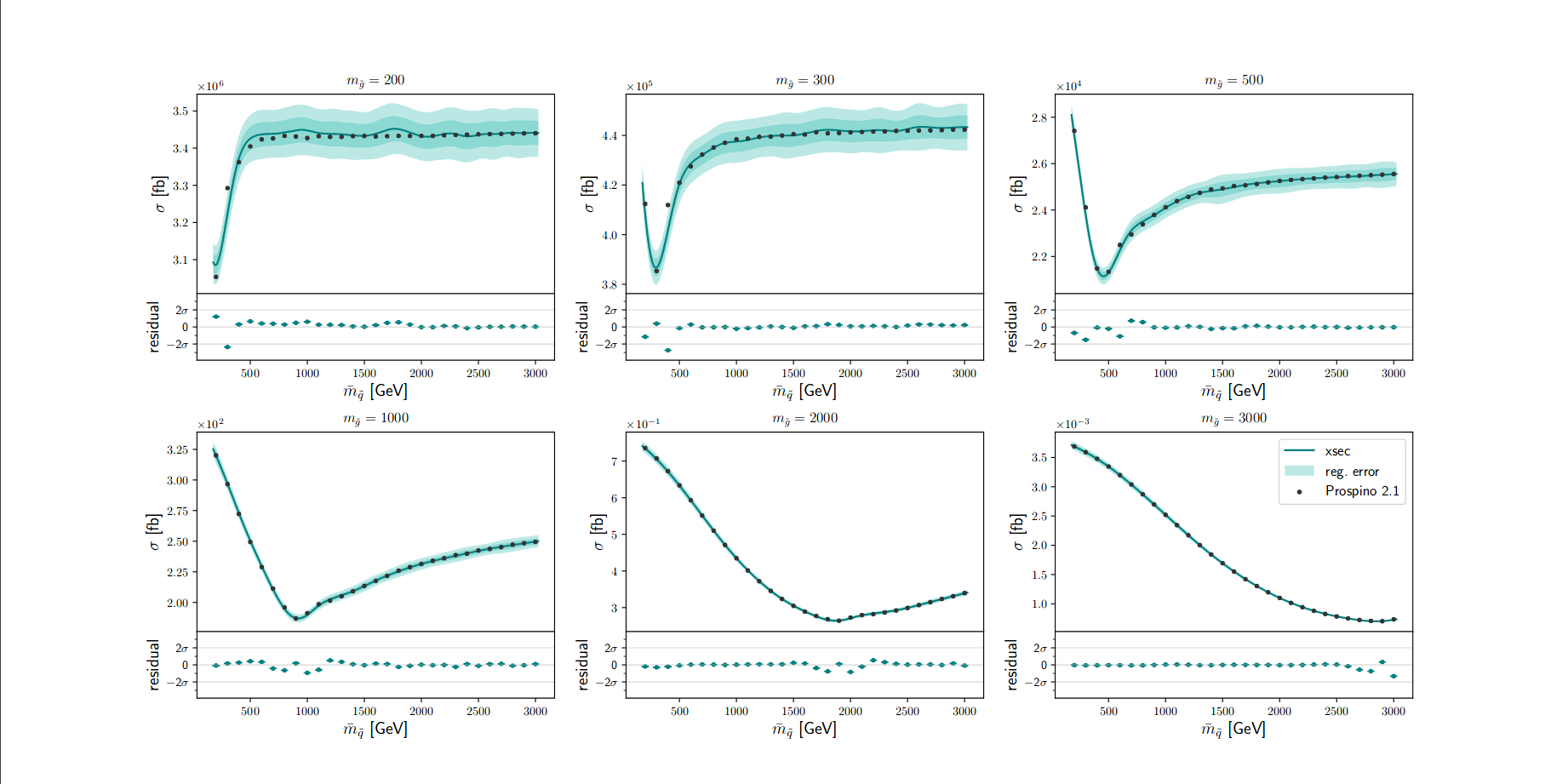
A quick example: gluino pair production at 13 TeV

Gaussian Processes 101

Radial Basis Function kernel

prior distribution over all functions

with the estimated smoothness

posterior distribution over functions

with updated \(m(\vec x)\)

data

Gaussian Processes 101

Matérn kernel

prior distribution over all functions

with the estimated smoothness

posterior distribution over functions

with updated \(m(\vec x)\)

data

All the scary math

Regression problem, with 'measurement' noise:

\(y=f(\vec x) + \varepsilon, \ \varepsilon\sim \mathcal{N}(0,\sigma_\varepsilon^2) \quad \rightarrow \quad \) infer \(f\), given data  \(\mathcal{D} = \{\vec X, \vec y\}\)

Assume covariance structure expressed by a kernel function, like

Consider the data as a sample from a multivariate Gaussian distribution.

\([\vec x_1, \vec x_2, \ldots]\)

\([y_1, y_2, \ldots]\)

signal kernel

white-noise kernel

All the scary math

Regression problem, with 'measurement' noise:

\(y=f(\vec x) + \varepsilon, \ \varepsilon\sim \mathcal{N}(0,\sigma_\varepsilon^2) \quad \rightarrow \quad \) infer \(f\), given data  \(\mathcal{D} = \{\vec X, \vec y\}\)

Training: optimise kernel hyperparameters by maximising the marginal likelihood

Posterior predictive distribution at a new point  \(\vec x_*\) :

with

Implicit integration over points not in  \(\vec X\)

[

All the scary math

Regression problem, with 'measurement' noise:

\(y=f(\vec x) + \varepsilon, \ \varepsilon\sim \mathcal{N}(0,\sigma_\varepsilon^2) \quad \rightarrow \quad \) infer \(f\), given data  \(\mathcal{D} = \{\vec X, \vec y\}\)

Training: optimise kernel hyperparameters by maximising the marginal likelihood

Posterior predictive distribution at a new point  \(\vec x_*\) :

with

Implicit integration over points not in  \(\vec X\)

[

My kingdom for a good kernel ...

GPs allow us to use probabilistic inference to learn a function from data, in an interpretable, analytical, yet non-parametric Bayesian framework.

A GP model is fully specified once the mean function, kernel and its hyperparameters are chosen.

The probabilistic interpretation only holds under the assumption that the chosen kernel accurately describes the true correlation structure.

e.g. correlation length scales

My kingdom for a good kernel ...

The choice of kernel allows for great flexibility. But once chosen, it fixes the type of functions likely under the GP prior and determines the kind of structure captured by the model, e.g., periodicity and differentiability.

[D. Duvenaud, PhD thesis ]

My kingdom for a good kernel ...

[D. Duvenaud, PhD thesis ]

The choice of kernel allows for great flexibility. But once chosen, it fixes the type of functions likely under the GP prior and determines the kind of structure captured by the model, e.g., periodicity and differentiability.

My kingdom for a good kernel ...

[D. Duvenaud, PhD thesis ]

The choice of kernel allows for great flexibility. But once chosen, it fixes the type of functions likely under the GP prior and determines the kind of structure captured by the model, e.g., periodicity and differentiability.

My kingdom for a good kernel ...

For our multi-dimensional case of cross-section regression, we get good results by multiplying Matérn (\(\nu = 3/2\)) kernels over the different mass dimensions:

The different lengthscale parameters  \(l_d\)  lead to automatic relevance determination for each feature: short-range correlations for important features over which the latent function varies strongly.

This is an anisotropic, stationary kernel. It allows for functions that are less smooth than with the standard squared-exponential kernel.

[Deisenroth+, unpublished]

... with good hyperparameters

Short lengthscale, small noise

Long lengthscale, large noise

Typically, kernel hyperparameters are estimated by maximising the (log) marginal likelihood \(p( \vec y\ |\ \vec X, \vec \theta) \), aka the empirical Bayes method.

Alternative: MCMC integration over a range of \(\vec \theta\).

Gradient-based optimisation is widely used, but can get stuck in local optima and plateaus. Multiple initialisations can help, or global optimisation methods like differential evolution.

... with good hyperparameters

Typically, kernel hyperparameters are estimated by maximising the (log) marginal likelihood \(p( \vec y\ |\ \vec X, \vec \theta) \), aka the empirical Bayes method.

Alternative: MCMC integration over a range of \(\vec \theta\).

Gradient-based optimisation is widely used, but can get stuck in local optima and plateaus. Multiple initialisations can help, or global optimisation methods like differential evolution.

Global optimum: somewhere in between

The standard approach systematically underestimates prediction errors.

After accounting for the additional uncertainty from learning the hyper-parameters, the prediction error increases when far from training points.

... with good hyperparameters

[Wågberg+, 1606.03865]

... with good hyperparameters

Other tricks to improve the numerical stability of training:

• Normalising features and target values (avoid meaningful zero prior)
• Factoring out known behaviour from the target values
• Training on log-transformed targets, for extreme values and/or a large range, or to ensure positive predictions

Sometimes, a curious problem arises: negative predictive variances!

It is due to numerical errors when computing the inverse of the covariance matrix \(K\). When \(K\) contains many training points, there is a good chance that some of them are similar:

signal-to-noise ratio

number of points

[Deisenroth+, unpublished]

GP Regularisation

GP Regularisation

• Use the Moore-Penrose matrix pseudo-inverse
  • Disregard redundant points,  averaging with zero uncertainty at repeated points
• Add a nugget/jitter term to the kernel
  • White noise, can compute minimal value that reduces \(\kappa\) below \(\kappa_\mathsf{max}\)
  • Can model discrepancy between GP model and latent function, e.g., regarding assumptions of stationarity and differentiability
• Avoid a large S/N ratio by adding a likelihood penalty term guiding the optimisation
  • Nearly noiseless data is problematic ... Artificially increasing the noise level may be necessary, degrading the model a bit

[Deisenroth+, unpublished]

[Mohammadi+, 1602.00853]

Workflow

Training scales as \(\mathcal{O}(n^3)\), prediction as \(\mathcal{O}(n^2)\)

A balancing act

Mix of random samples with different priors in mass space

Evaluation speed

Sample coverage

Need to cover a large parameter space

Distributed Gaussian processes

[Liu+, 1806.00720]

Generalized Robust Bayesian Committee Machines

Aggregation model for dealing with large datasets

1. Split the data into 1 global communication set \(\mathcal D_c\) and any number of local expert sets \(\mathcal D_i\)
2. Train a separate GP on each data set
3. Augment \(\mathcal D_i\) with \(\mathcal D_c\) , without re-training
4. Combine predictions from the separate GPs, giving larger weight to experts with small uncertainty

Goal

$$ pp\to\tilde g \tilde g,\ \tilde g \tilde q_i,\ \tilde q_i \tilde q_j, $$

$$\tilde q_i \tilde q_j^{*},\ \tilde b_i \tilde b_i^{*},\ \tilde t_i \tilde t_i^{*}$$

Interface

Method

Pre-trained, distributed Gaussian processes

Stand-alone Python code, also implemented in GAMBIT

Processes

Soon public on GitHub!

Thank You!