Turning up the (re)heat with gravitino dark matter
Jeriek Van den Abeele

3rd N-PACT Meeting
Oslo – August 6, 2019

based on ongoing work with J. Heisig, J. Kersten and I. Strümke
A recipe for a universe
1. Start with a hot, dense state
2. Let quantum gravity do its thing for the first \(10^{-43}\) s
3. While cooling: separate gravity, the strong and electroweak forces
4. Rapidly inflate to \(> 10^{78}\) times its volume, before \(t\sim 10^{-32}\) s
5. Reheat and fill with a quark-gluon plasma
6. Break supersymmetry and electroweak symmetry (\(t\sim 10^{-12}\) s)
7. Add (anti)hadrons in a good balance, leaving \(n^0:p^+=1:7\) after 1 s

A recipe for a universe
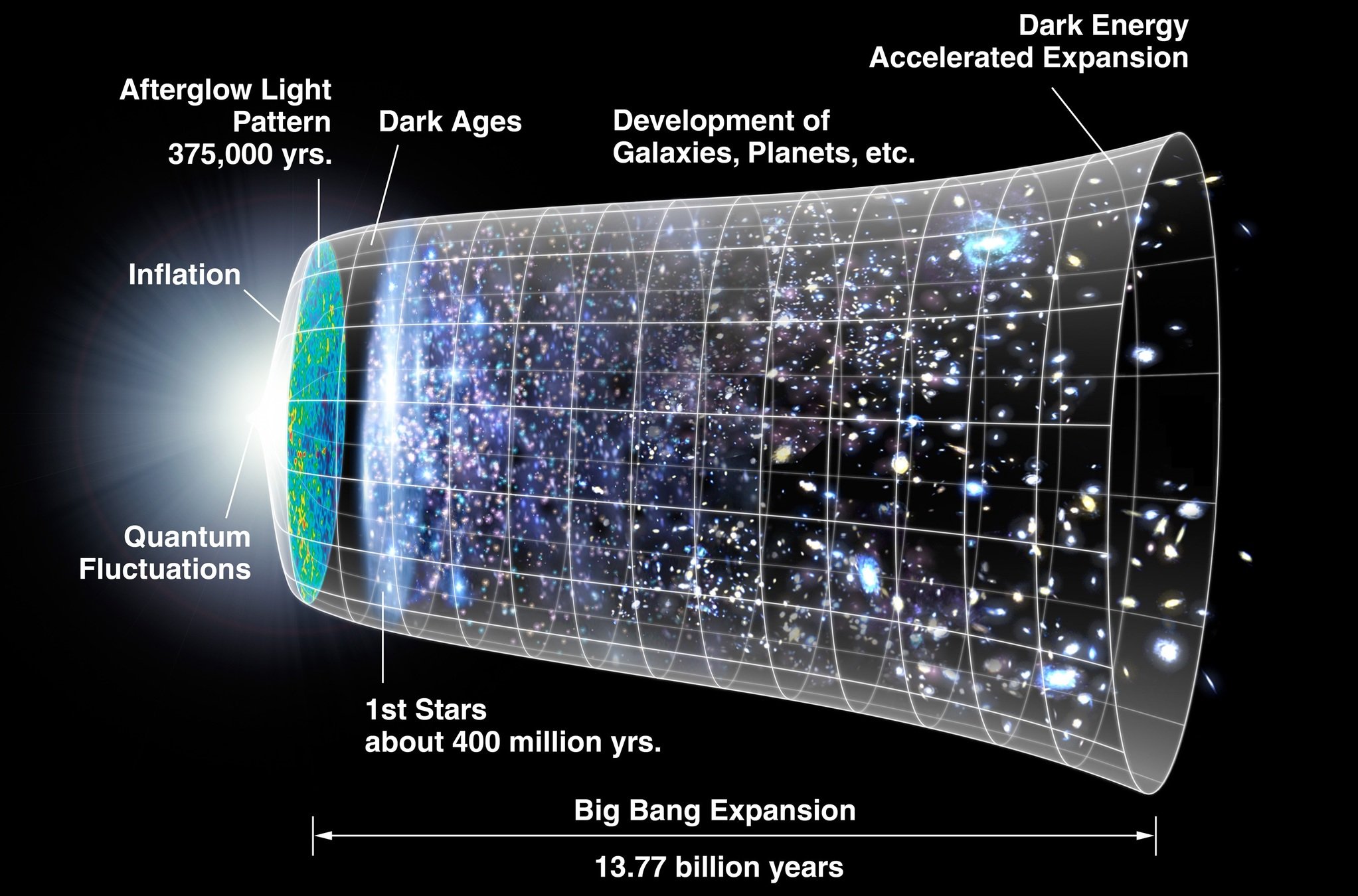
Image: NASA/WMAP
A recipe for a universe
8. After simmering, decouple neutrinos and annihilate most leptons
9. Cool for 100 s, then synthesise light elements for 20 mins.
10. Stir dark matter into filaments after ~ 47 000 yr, matter will follow
11. Wait 330 000 yr before creating atoms, and let photons escape
12. Set a timer for \(\sim 10^8\) yr, take a nap while gravity works its magic
13. Decorate with stars and galaxies and stuff
14. Accelerate your universe's expansion; come up with a fun finale!

How to get more stuff than anti-stuff
To succeed, Big Bang nucleosynthesis requires \(\frac{n_B-n_{\bar B}}{n_\gamma}\sim 10^{-9}\).
The Sakharov conditions for generating a baryon asymmetry dynamically:
- Baryon number violation (of course)
- C and CP violation (else: same rate for matter and anti-matter creation)
- Departure from thermal equilibrium (else: same abundance anti-particles, given CPT)
Not satisfied in the Standard Model.
Baryogenesis via thermal leptogenesis provides a minimal realisation, only requiring heavy right-handed neutrinos \(N_i\) (\(\rightarrow m_\nu\) via see-saw mechanism):
out-of-eq. CP-violating \(N\) decays at \(T\sim m_N\) cause lepton asymmetry
baryon asymmetry
SM sphalerons
Serious SUSY shopping list
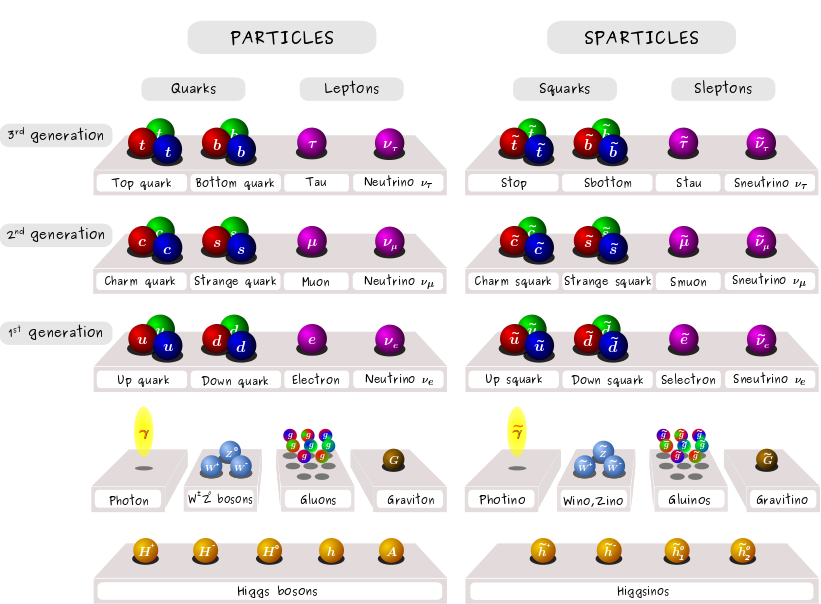
Image: Claire David (CERN)
(+ RH neutrinos)
Gravitino trouble
Given R-parity, the LSP is stable and a dark matter candidate.
In a neutralino LSP scenario with \(m_{\tilde G}\sim m_\mathsf{SUSY}\):
- Thermal scattering during reheating produces gravitinos with \(\Omega^\mathsf{th}_{\tilde G} \propto T_R\)
- Thermal leptogenesis needs \(T_R \gtrsim 10^9\) GeV, to match observed \(\frac{n_B}{n_\gamma}\) and \(m_\nu\)
-
Due to \(M_\mathsf{Pl}\)-suppressed couplings, the gravitino easily becomes long-lived: \[\tau_{\tilde G} \sim 10^7~\mathsf{s} \left(\frac{100~\mathsf{GeV}}{m_{\tilde G}} \right)^3\]
-
Overabundant, delayed gravitino decays disrupt BBN, excluding \(T_R \gtrsim 10^5\) GeV!
So ... why not try a gravitino LSP (with neutralino NLSP)?
Gravitino trouble
Given R-parity, the LSP is stable and a dark matter candidate.
In a gravitino LSP scenario:
- Planck-suppressed widths make the NLSP long-lived and a danger to BBN
- Thermal leptogenesis still needs \(T_R \gtrsim 10^9\) GeV
-
Now, for an MSSM NLSP, thermal freeze-out (not \(T_R\)!) determines the abundance
-
\(\Omega^\mathsf{th}_\mathsf{NLSP}\) is controlled by MSSM parameters; if it is low, the BBN impact is minimal!

The heavy Higgs funnel
Parameter region where the neutralino NLSP dominantly annihilates via resonant heavy Higgs bosons: \[2m_{\tilde \chi_{1}^{0}} \approx m_{H^0/A^0}\]
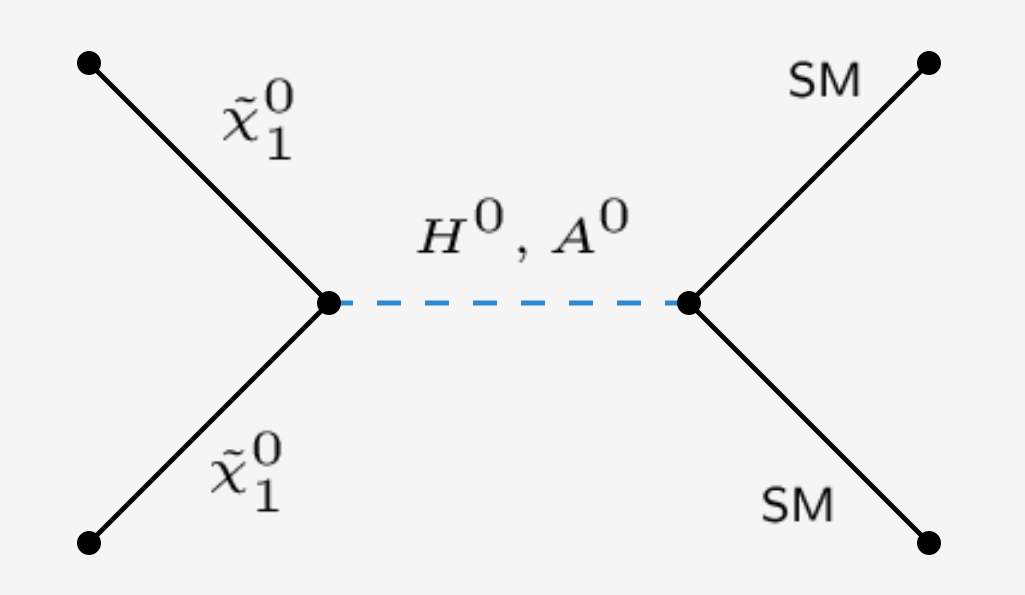
- Requires wino-higgsino NLSP
-
Open window facilitating tiny NLSP freeze-out abundance
- Avoids injecting too much energy into BBN
- Minimises non-thermal gravitino abundance contribution from NLSP decays
Gravitino production
The gravitino relic density should match the observed \[\Omega_\mathsf{DM} h^2 = 0.1199\pm 0.0022\]
No thermal equilibrium for gravitinos in the early universe, due to superweak couplings (unless very light, but then no longer DM candidate due to Lyman-\(\alpha\))
So no standard mechanism to lower the gravitino abundance: instead, gradual build-up!
- UV-dominated freeze-in from thermal scatterings at \(T\sim T_R\) \[\Omega_{\tilde G}^{\textsf{UV}} h^2 = \left( \frac{m_{\tilde{G}}} {100 \, \textsf{GeV}} \right)\! \left(\frac{T_{\textsf{R}}}{10^{10}\,\textsf{GeV}}\right)\! \left[\,\sum_{i=1}^{3}\omega_i g_i^2 \! \left(1+\frac{M_i^2}{3m_{\tilde{G}}^2}\right) \ln\!\left(\frac{k_i}{g_i}\right) + 0.00319\, y_t^2\!\left(1+\frac{A_t^2}{3m_{\tilde{G}}^2}\right)\right]\] (accounting for 1-loop running of \(g_i, M_i, y_t, A_t\))
- IR-dominated freeze-in from decays of heaviest sparticles
- SuperWIMP contribution from decays of thermal neutralino NLSP
- (Direct inflaton decays to gravitinos)
from processes like \((g+g\rightarrow) g \rightarrow \tilde g + \tilde G \)
Gravitino production
The gravitino relic density should match the observed \[\Omega_\mathsf{DM} h^2 = 0.1199\pm 0.0022\]
No thermal equilibrium for gravitinos in the early universe, due to superweak couplings (unless very light, but then no longer DM candidate due to Lyman-\(\alpha\))
So no standard mechanism to lower the gravitino abundance: instead, gradual build-up!
- UV-dominated freeze-in from thermal scatterings at \(T\sim T_R\)
- IR-dominated freeze-in from decays of heaviest sparticles \[\Omega_{\tilde G}^{\textsf{IR}}h^2 \simeq 0.0035 \left(\frac{915/4}{g_*}\right)^{\!3/2} \left(\frac{100 \,\mathsf{GeV} }{ m_{\tilde G}}\right) \, \sum_i g_{\widetilde f_i} \left(\frac{m_{\widetilde f_i} }{ 10^5 \,\mathsf{GeV} } \right)^{\!3}\]
- SuperWIMP contribution from decays of thermal neutralino NLSP
- (Direct inflaton decays to gravitinos)
Gravitino production
The gravitino relic density should match the observed \[\Omega_\mathsf{DM} h^2 = 0.1199\pm 0.0022\]
No thermal equilibrium for gravitinos in the early universe, due to superweak couplings (unless very light, but then no longer DM candidate due to Lyman-\(\alpha\))
So no standard mechanism to lower the gravitino abundance: instead, gradual build-up!
- UV-dominated freeze-in from thermal scatterings at \(T\sim T_R\)
- IR-dominated freeze-in from decays of heaviest sparticles
- SuperWIMP contribution from decays of thermal neutralino NLSP \[\frac{\Omega_{\tilde G}^\mathsf{SW}h^2}{m_{\tilde G}} = \frac{\Omega_{\tilde \chi}^\mathsf{th} h^2}{m_{\tilde \chi}}\]
- (Direct inflaton decays to gravitinos)
BBN constraints
Lifetime/abundance limits for a generic particle decaying into \[u\bar u, b\bar b, t\bar t, gg, e^+e^-, \tau^+\tau^-, \gamma\gamma, W^+W^-\] and thus injecting energy into the primordial plasma
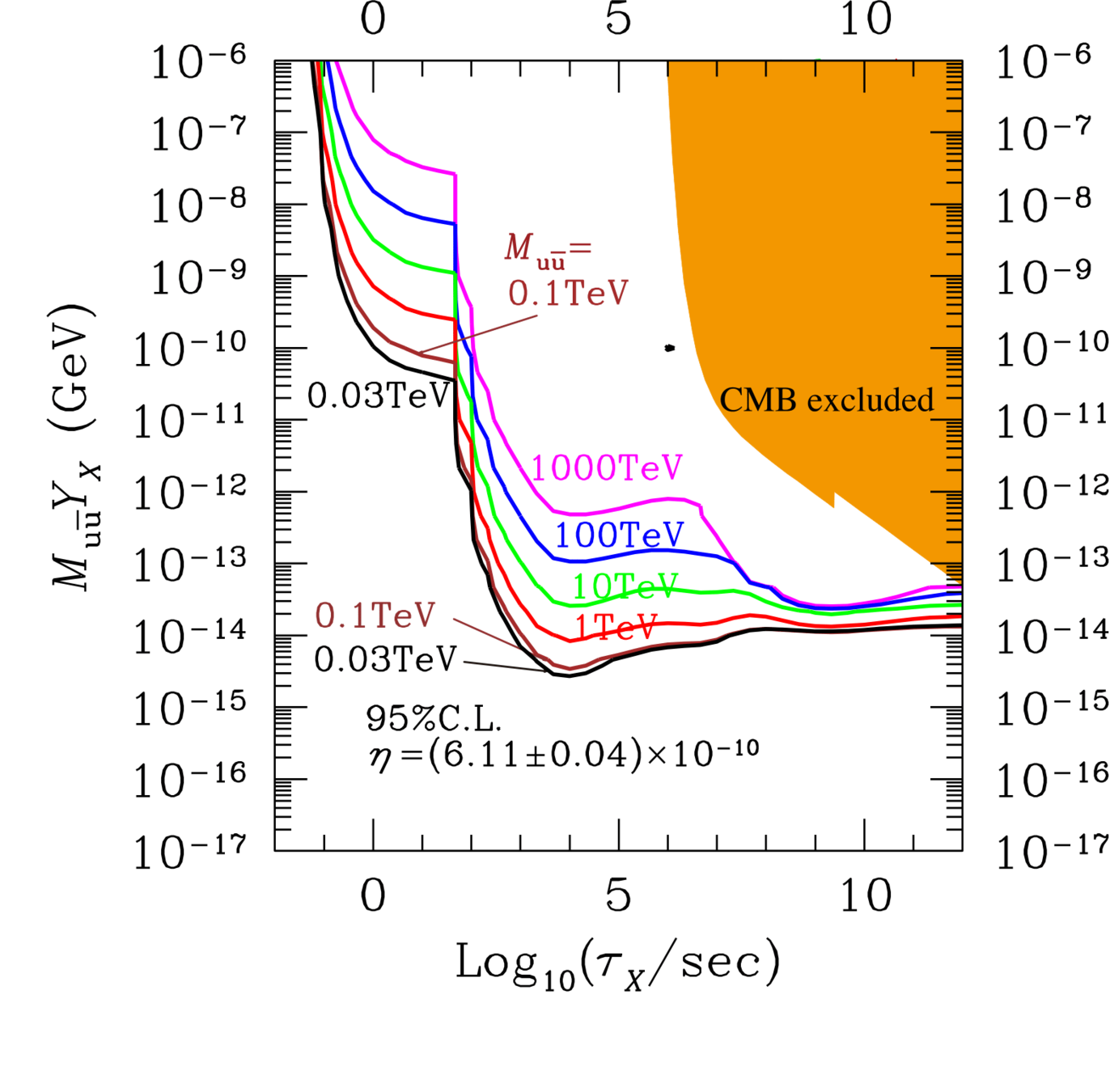
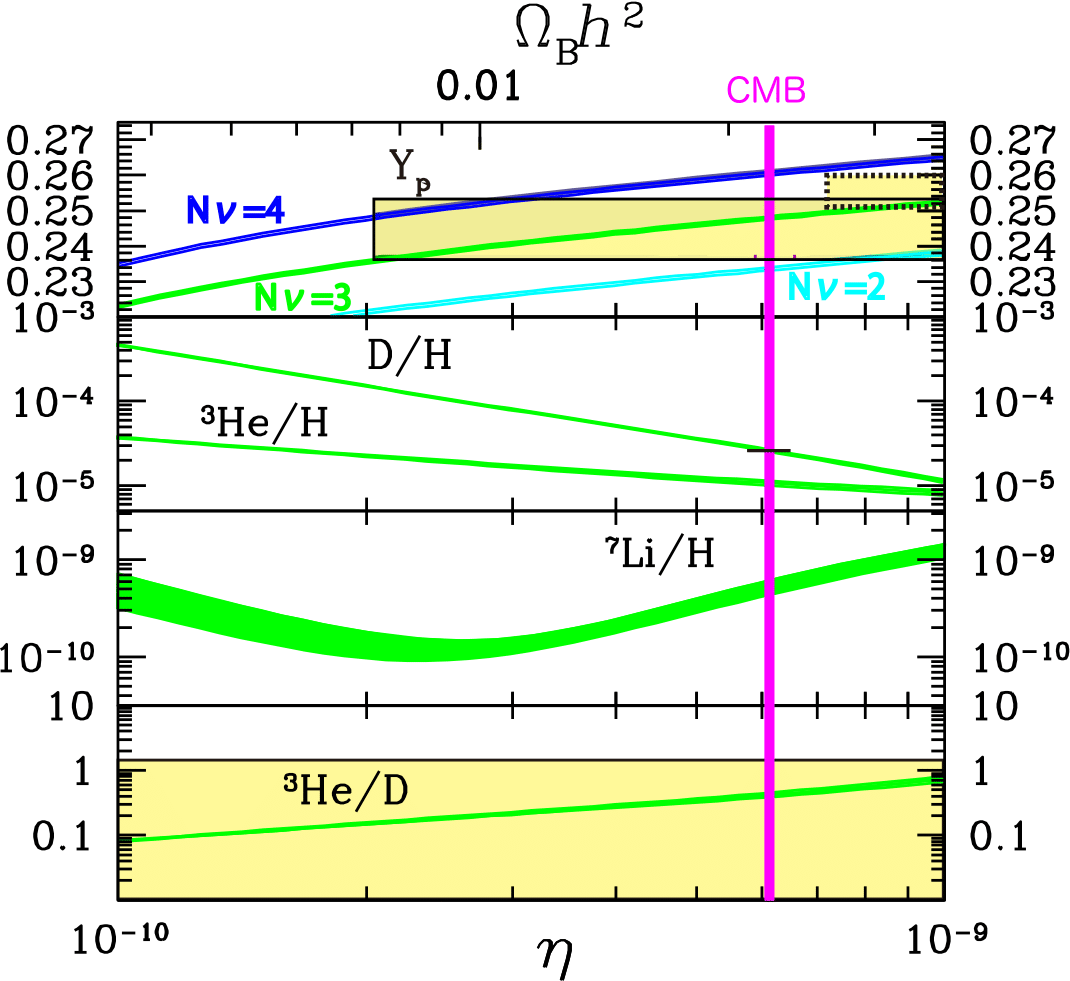
arXiv:1709.01211
p/n conversion
hadrodissociation
photodissociation
NLSP decays
\(\tilde{\chi}_1^0 \to \tilde{G} + \gamma \)
\(\tilde{\chi}_1^0 \to \tilde{G} + Z \)
\(\tilde{\chi}_1^0 \to \tilde{G} + \gamma^* \to \tilde{G} + f \bar{f} \qquad \mathsf{for } f = u,d,s,c,b,t, e, \mu, \tau\)
\(\tilde{\chi}_1^0 \to \tilde{G} + Z^{*} \to \tilde{G} + f \bar{f} \qquad \mathsf{for } f = u,d,s,c,b,t, e, \mu, \tau\)
\(\tilde{\chi}_1^0 \to \tilde{G} + (\gamma/Z)^{*} \to \tilde{G} + f \bar{f} \qquad \mathsf{for } f = u,d,s,c,b,t, e, \mu, \tau\)
\(\tilde{\chi}_1^0 \to \tilde{G} + h^0 \to \tilde{G} + XY \qquad \mathsf{for } XY = \mu^+\mu^-,\tau^+\tau^-, c\bar c, b \bar b, g g, \gamma \gamma, Z \gamma, ZZ, W^+ W^-\)
Relevant decay channels:
Crucially, the NLSP lifetime behaves as \(\tau_{\tilde \chi} \propto M_P^2 m_{\tilde G}^2/m_{\tilde \chi}^5 \) !
Collider constraints
Last step due to computational expense, split into 5 components:
- Quick veto with lower bound on EWino masses, upper bound on lifetimes and pass some gluino/neutralino exclusion limits from ATLAS search [1712.02332]
- Quick veto on chargino production cross-section from CMS disappearing-track search [1804.07321]
- SmodelS determines simplified model topologies and tests them against LHC limits
- CheckMATE performs event generation, detector simulation, cuts for different signal regions, and applies LHC limits from 8 and 13 TeV analyses
- HiggsBounds checks Higgs sector predictions against LEP/Tevatron/LHC limits
Guided scan strategy
Construct a likelihood \(\mathcal{L}_\mathsf{scan} = \mathcal{L}_\mathsf{relic\ density} \times \mathcal{L}_\mathsf{BBN} \times \mathcal{L}_\mathsf{collider} \times \mathcal{L}^\mathsf{fake}_\mathsf{T_R}\).
Nested sampling with MultiNest to zone in on region with highest \(\mathcal{L}_\mathsf{scan}\):
- Focusing on funnel region and guided towards high \(\mathsf{T_R}\)
- 7 parameters varied in the scan: \(T_R, m_{\tilde G}, M_1, M_2, M_3, \mu, A_0\)
- Fixed \(\tan \beta = 10\) and \(m_{scalars} = 15\ \mathsf{TeV}\)
-
External dependencies:
- SOFTSUSY (spectrum generation)
- MicrOMEGAs (thermal NLSP abundance, chargino production cross sections)
- SmodelS, CheckMATE [ROOT, Delphes, MadGraph, Pythia, HepMC], HiggsBounds (collider checks)
Some preliminary results
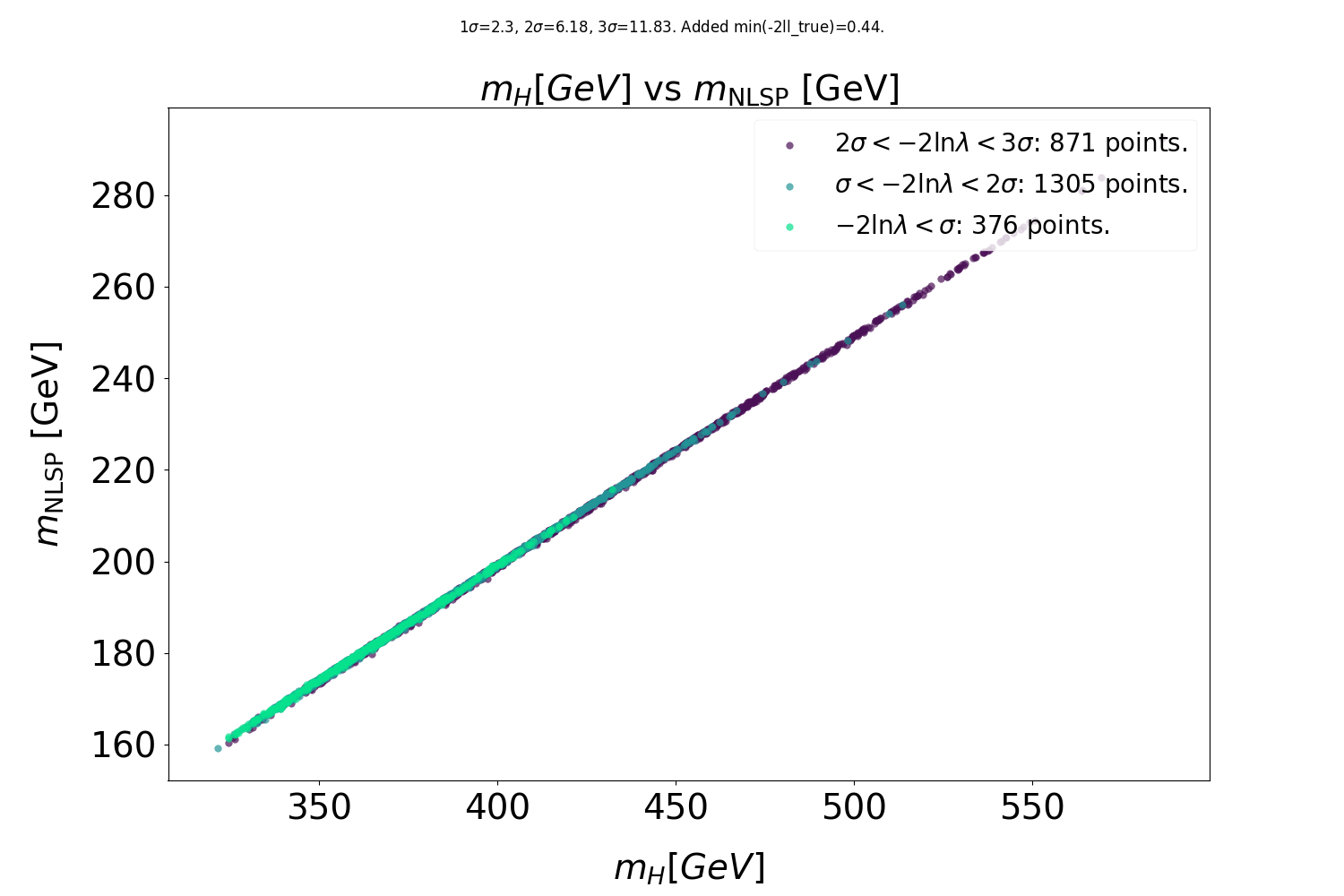
Preliminary
Some preliminary results
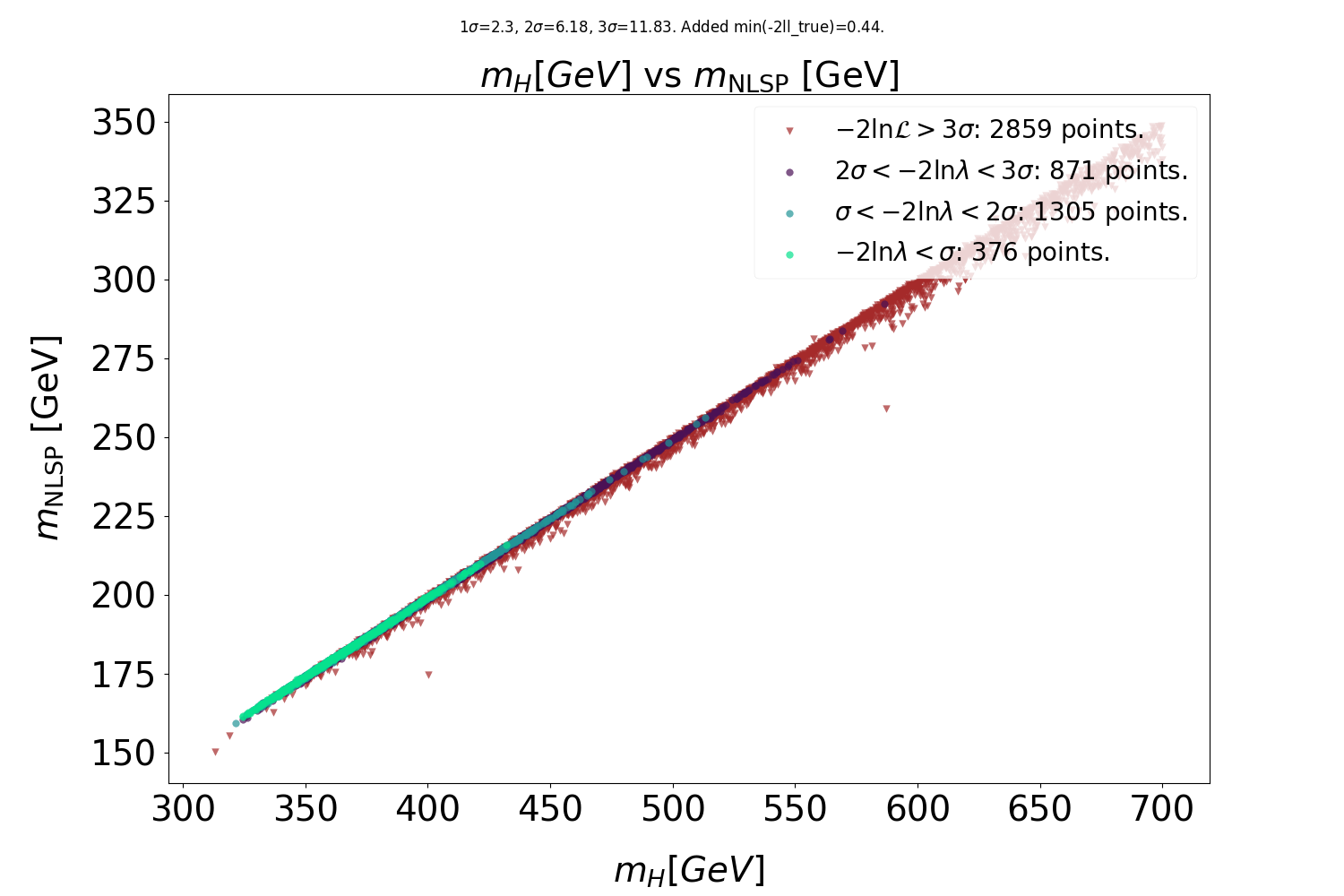
Preliminary
Some preliminary results
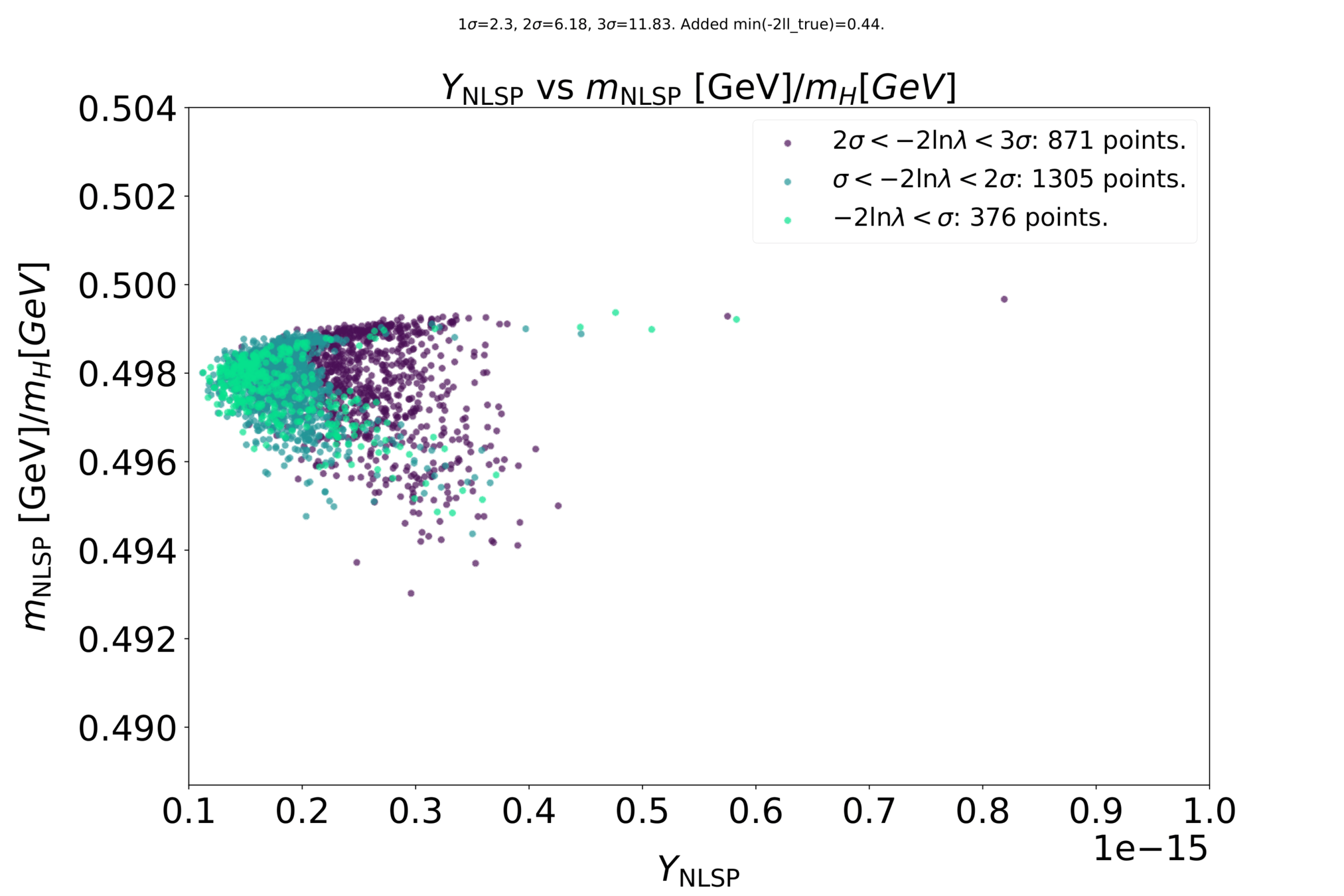
Preliminary
Some preliminary results
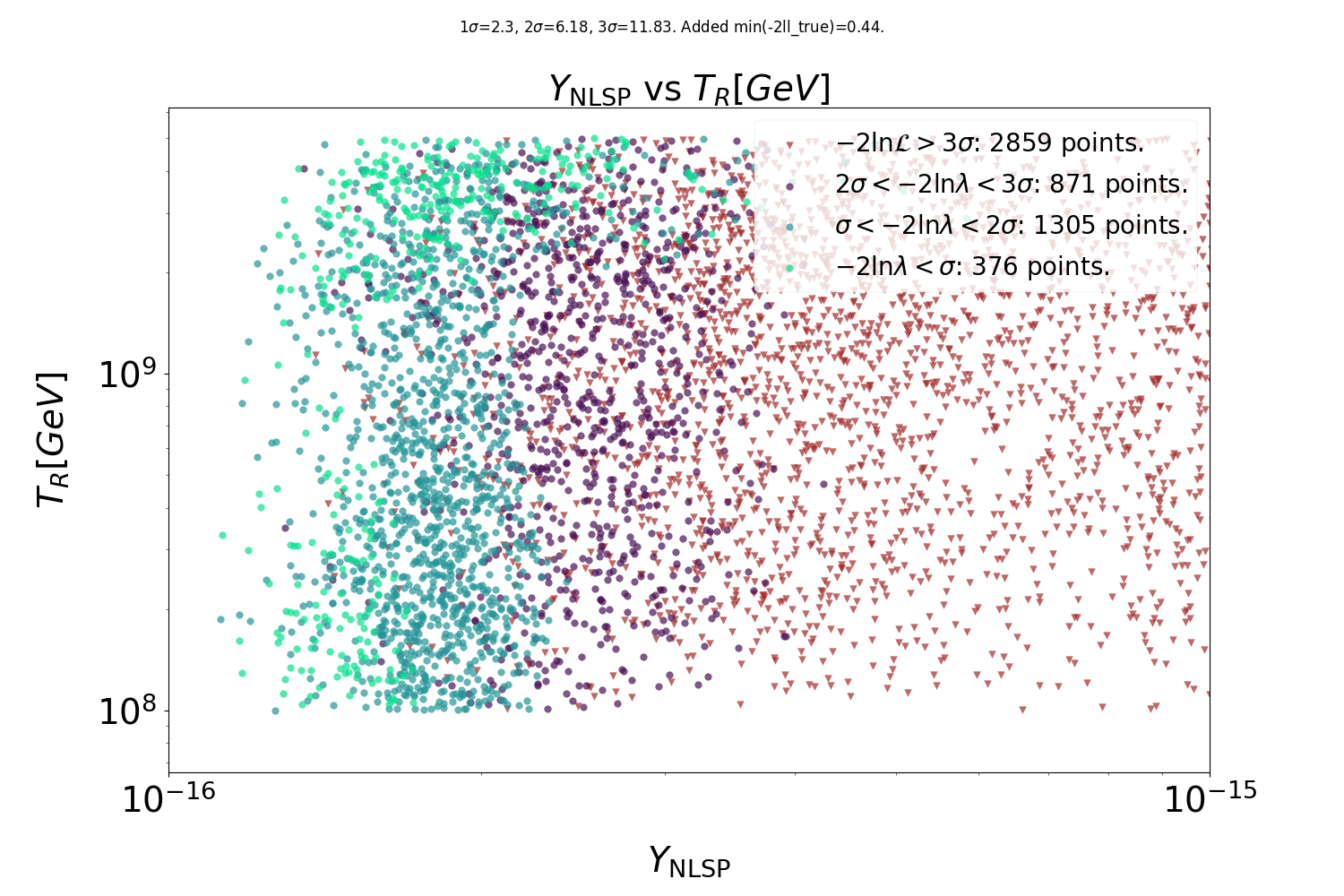
Preliminary
Some preliminary results
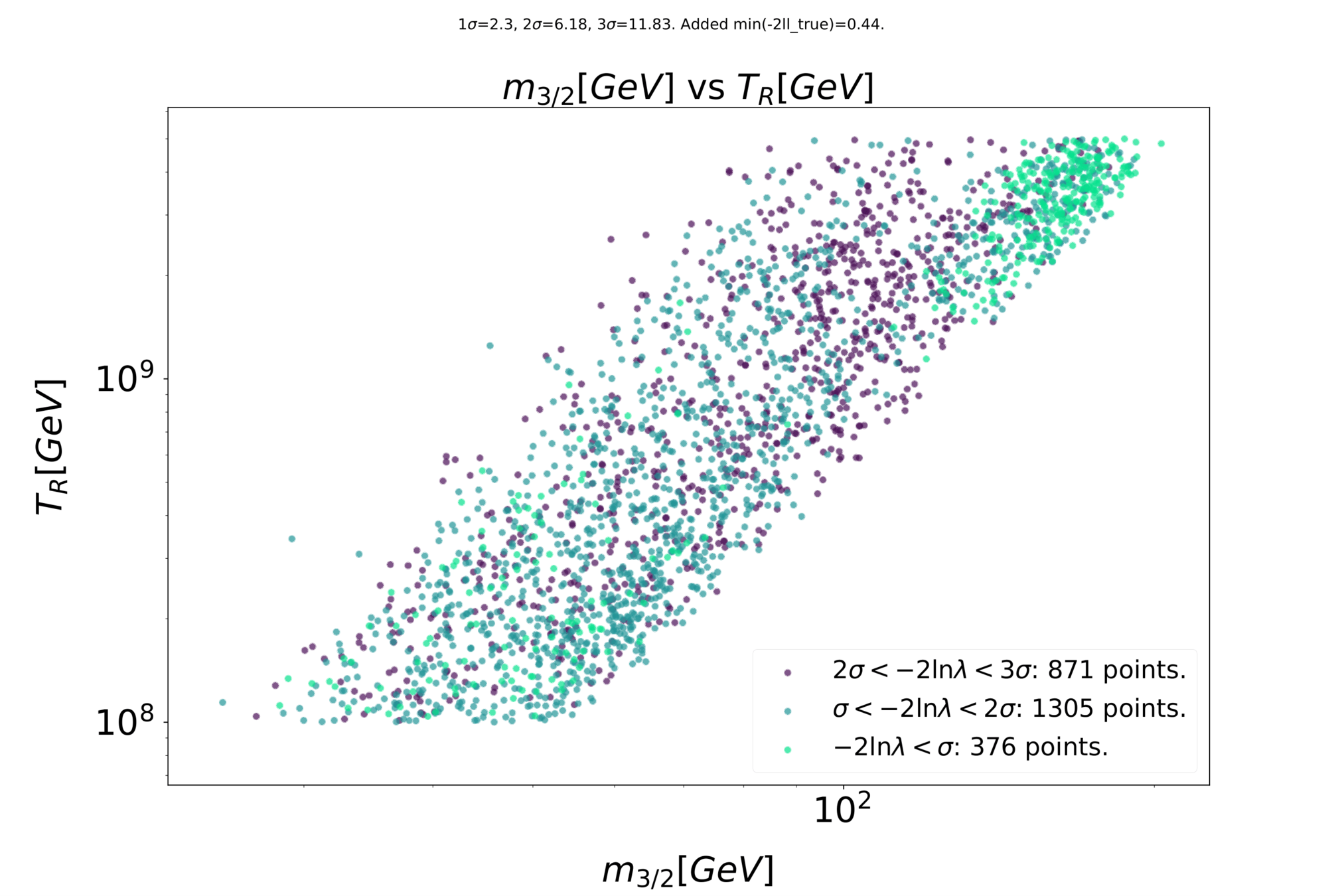
Preliminary
Some preliminary results
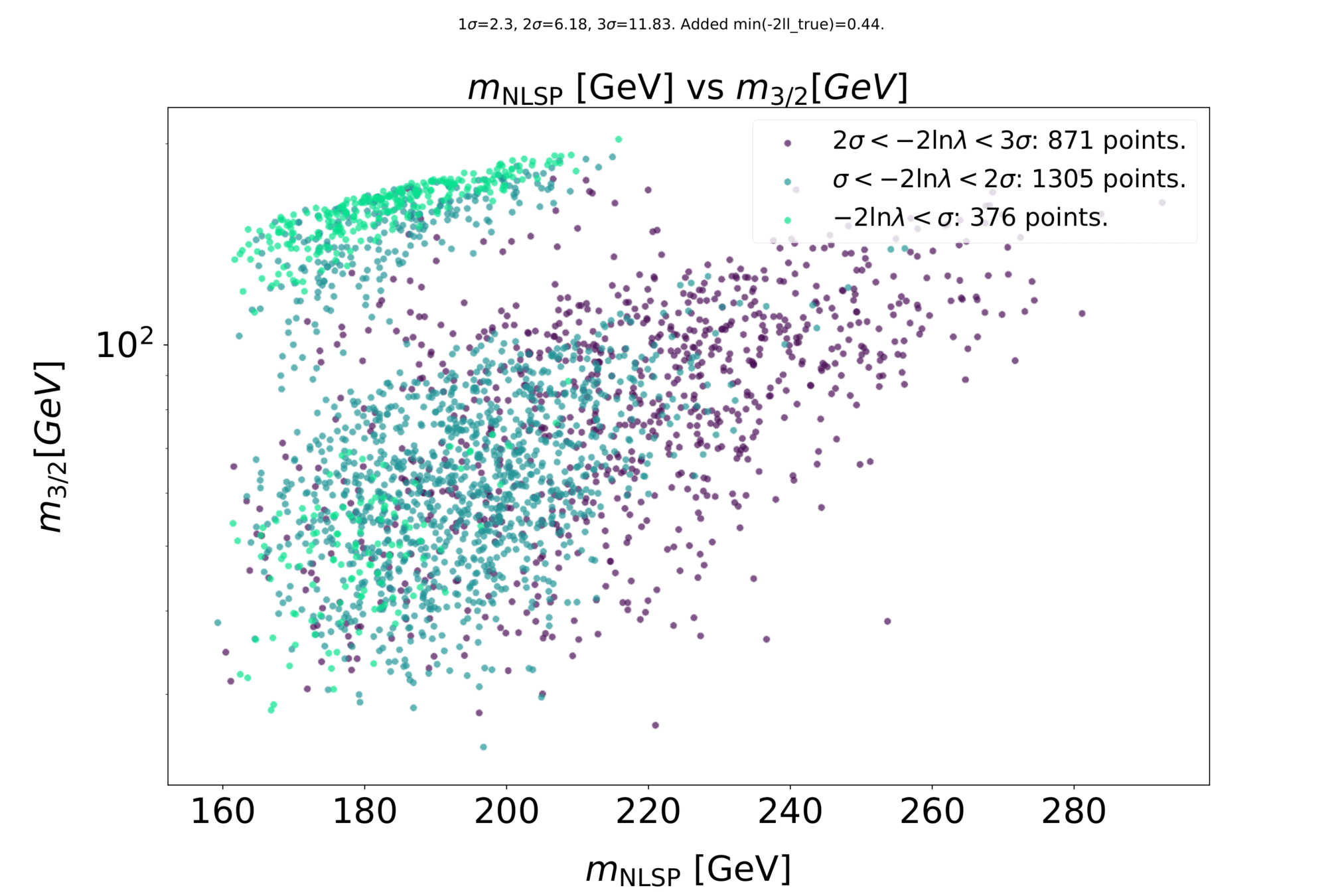
Preliminary
To be continued ...

Turning up the (re)heat with gravitino dark matter
By jeriek
Turning up the (re)heat with gravitino dark matter
- 478



