1. Introduction

Three strategies to live in uncertain environments

Cells need to continuously adapt to an uncertain environment.

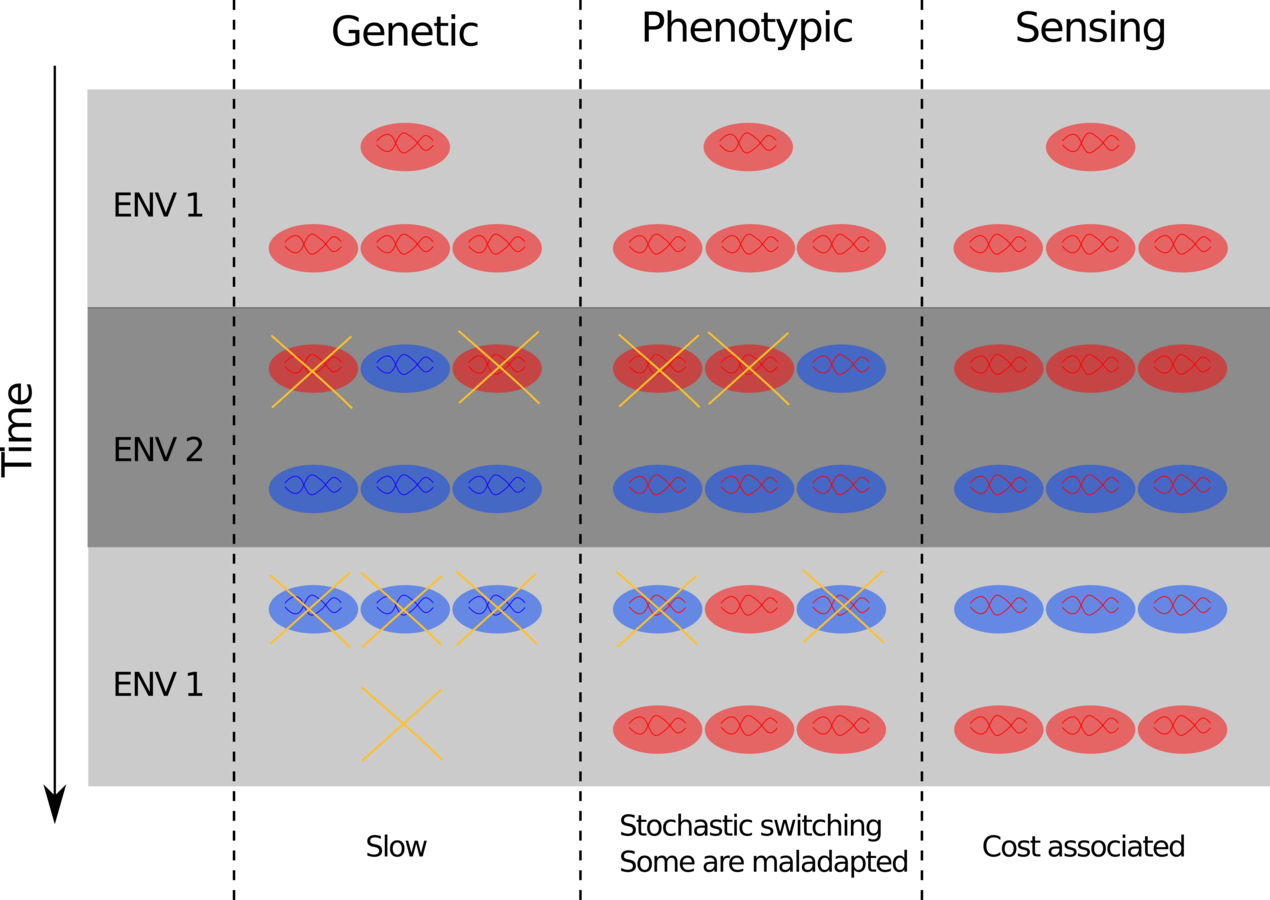
Three strategies to live in uncertain environments

Cells need to continuously adapt to an uncertain environment.

Three strategies to live in uncertain environments

Cells need to continuously adapt to an uncertain environment.

Three strategies to live in uncertain environments

Cells need to continuously adapt to an uncertain environment.

Examples of phenotypic diversity: 

Delayed germination of seeds

Phenotypes switching rate.

- One Genotype, Several phenotypes

Environment transition rate.

- One environment, Several states

Three strategies to live in uncertain environments

Cells need to continuously adapt to an uncertain environment.

Three strategies to live in uncertain environments

Cells need to continuously adapt to an uncertain environment.

parts of the game determining strategies

• 1. Players
  • Cells in a population
    • Cooperation between cells

parts of the game determining strategies

• 1. Players
  • Cells in a population
    • Cooperation between cells
• 2. Actions 
  • Sense the environment
  • Switch between phenotype states

parts of the game determining strategies

• 1. Players
  • Cells in a population
    • Cooperation between cells
• 2. Actions 
  • Sense the environment
  • Switch between phenotype states
• 3. Information
  • Environment

parts of the game determining strategies

• 1. Players
  • Cells in a population
    • Cooperation between cells
• 2. Actions 
  • Sense the environment
  • Switch between phenotype states
• 3. Information
  • Environment
• 4. Payoffs
  • Growth rate

Strategy: Some actions that maximize payoff

parts of the game determining strategies

• 1. Players
  • Cells in a population
    • Cooperation between cells
• 2. Actions 
  • Sense the environment
  • Switch between phenotype states
• 3. Information
  • Environment
• 4. Payoffs
  • Growth rate

The best known equilibrium in biology is known as the evolutionarily stable strategy (ESS), first introduced in (Smith & Price 1973).

Strategy: Some actions that maximize payoff

parts of the game determining strategies

• 1. Players
  • Cells in a population
    • Cooperation between cells
• 2. Actions 
  • Sense the environment
  • Switch between phenotype states
• 3. Information
  • Environment
• 4. Payoffs
  • Growth rate

What has been done

Dr. Richard Levins (1930-). 

Evolution in Changing Environments, 1968

Analytic and in vivo experiments with two phenotypes and two environments.

The optimal strategy depends on:

• Cost of sensing.
• Time spent at each environmental state.
• Frequency of environmental transitions.
• Growth rate of each phenotype in the two environment states.
• Information about future conditions.

Text

Acar and van Oudenaarden (Nature, 2008)

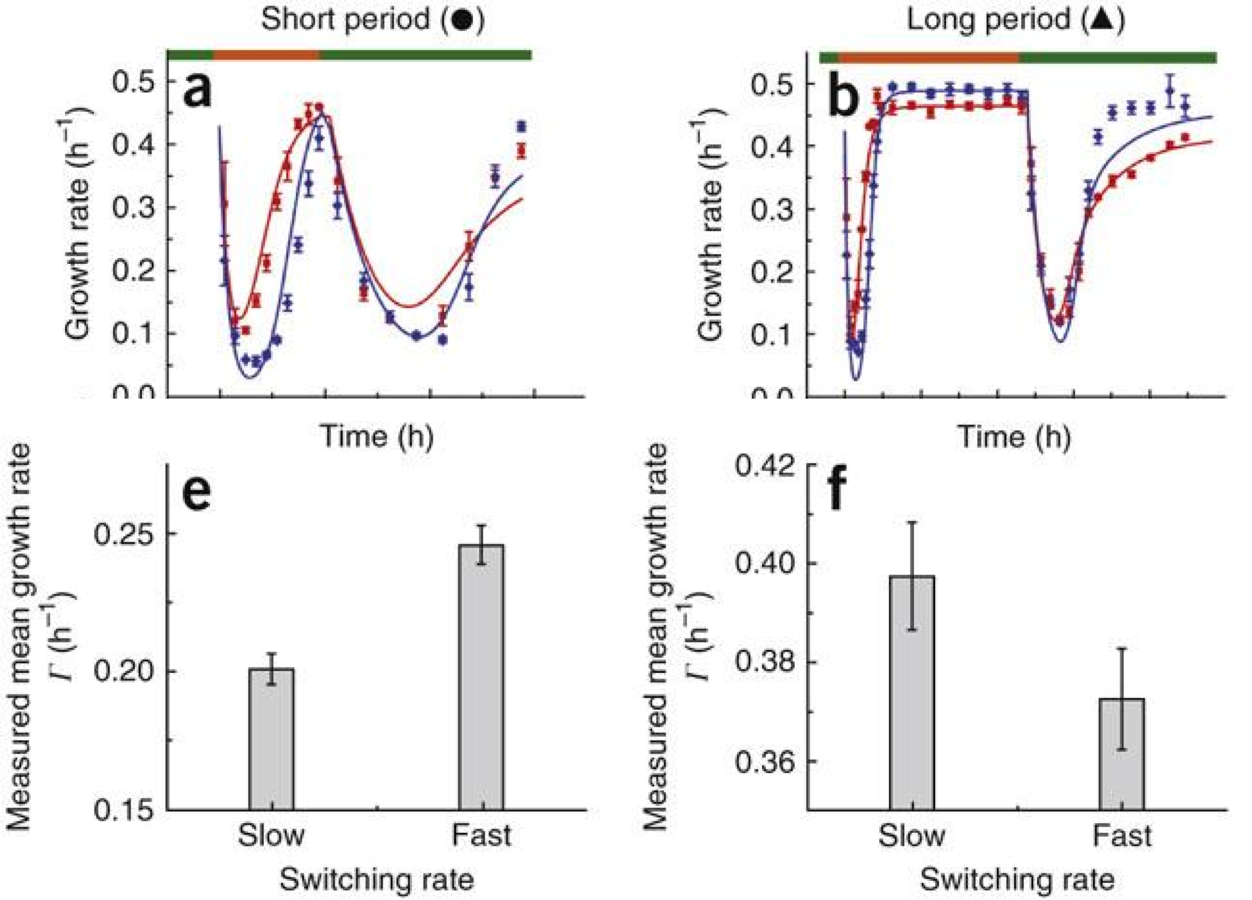
Population of cells with fast switching rates between phenotypes have higher growth rates in environments with fast transitions between states.

Population of cells with slow switching rates between phenotypes have higher growth rates in environments with slow transitions between states.

What are we proposing

• Use evolutionary algorithms to find optimal strategies of growth in fluctuating environments.
  • Analytic/Numeric solutions are not easy when sensing is allowed and the number of environment increases.

What are we proposing

• Use evolutionary algorithms to find optimal strategies of growth in fluctuating environments.
  • Analytic/Numeric solutions are not easy when sensing is allowed and the number of environment increases.
  • We focus on stress response.
    • Populations of cells living in an uncertain environment.
    • Presence of a stressor can be fatal if the sensory response is too slow compared with the environmental transition rate.
    • Several strategies have been observed in vivo.
      • ​Multistability vs Continuous phenotype
      • Sensing vs No sensing

Elowitz lab

What are we proposing

• Use evolutionary algorithms to find optimal strategies of growth in fluctuating environments.
  • Analytic/Numeric solutions are not easy when sensing is allowed and the number of environment increases.
  • We focus on stress response.
    • Populations of cells living in an uncertain environment.
    • Presence of a stressor can be fatal if the sensory response is too slow compared with the environmental transition rate.
    • Several strategies have been observed in vivo.
      • ​Multistability vs Continuous phenotype
      • Sensing vs No sensing
  • Proof of concept: Two environmental states

• Phenotype: Level of a hypothetical protein involved in stress response
• We will evolve the distribution of protein expression in the population when no stressor is present. 

What are we proposing

When stressor is present, the population either senses it and adapts perfectly, or continues with the same distribution.

What are we proposing

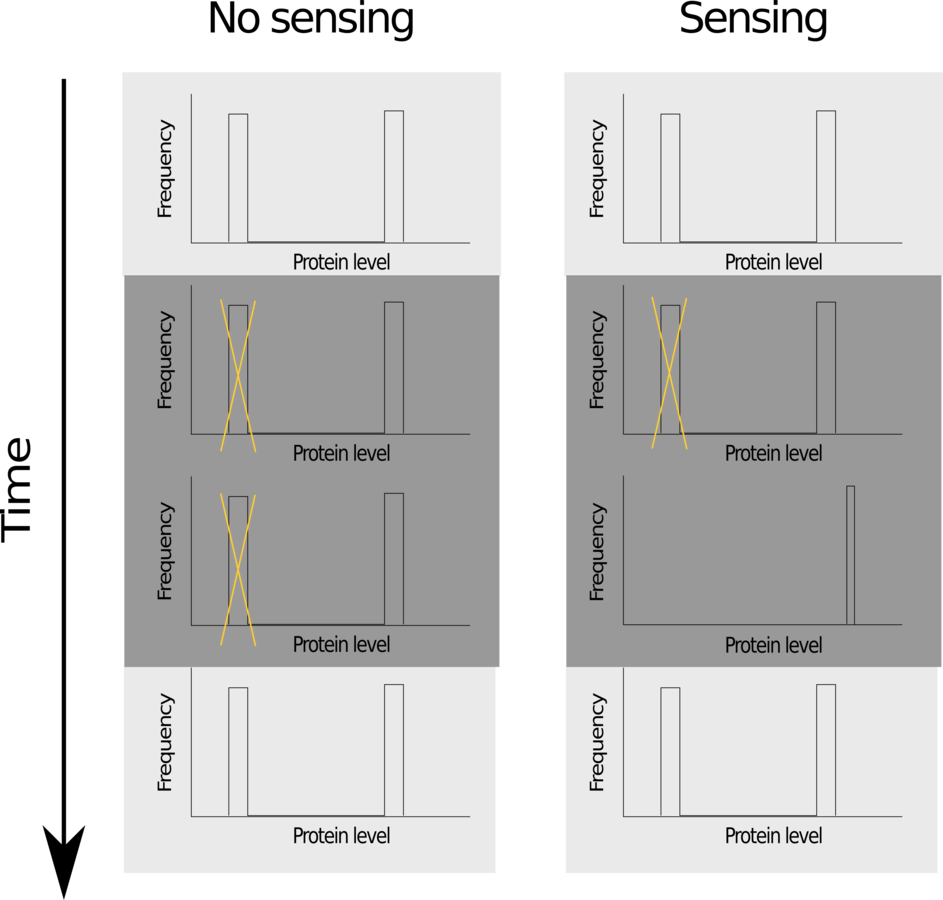
When stressor is present, the population either senses it and adapts perfectly, or continues with the same distribution.

What are we proposing

What are we proposing

• The strategies with many environmental states and many phenotypes (or a continuous phenotype) have not been studied.

• Is a finite number of phenotypes (multistability) better than continuous phenotype?
  • Many biological examples with a continuous phenotype.
  • Some advantages of a continuous phenotype:
    • Require small genetic networks
    • Evolvability
  • ​​Some disadvantages:
    • ​Many intermediate states, that can decrease fitness.

What are we proposing

• The strategies with many environmental states and many phenotypes (or a continuous phenotype) have not been studied.

• Is a finite number of phenotypes (multistability) better than continuous phenotype?
  • Many biological examples with a continuous phenotype.
  • Some advantages of a continuous phenotype:
    • Require small genetic networks
    • Evolvability
  • ​​Some disadvantages:
    • ​Many intermediate states, that can decrease fitness.
• Hypothesis: A continuous phenotype is better or similar when many environmental states and many phenotype options are possible.

What are we proposing

• The strategies with many environmental states and many phenotypes (or a continuous phenotype) have not been studied.

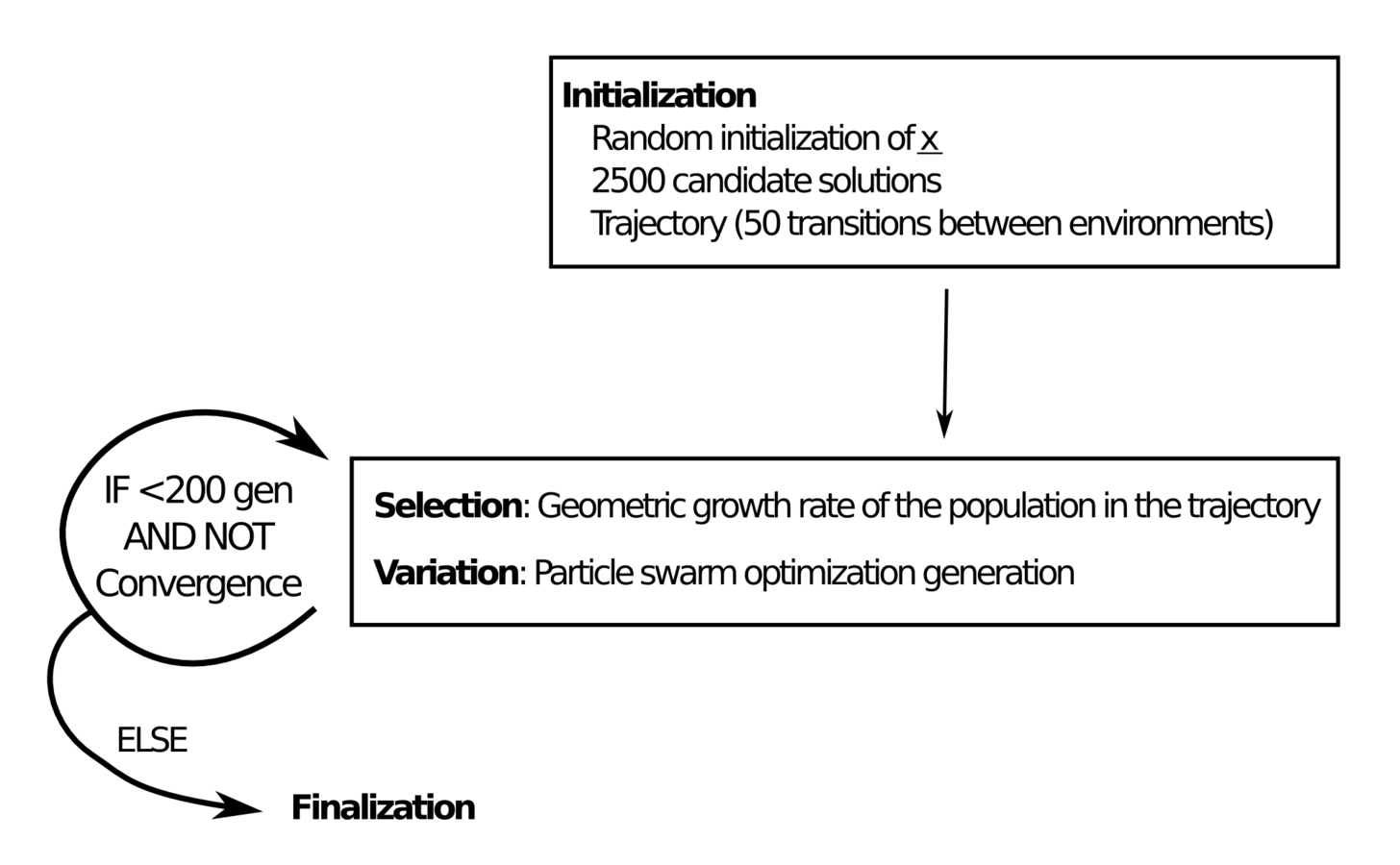
2. Methods

We use evolutionary algorithms

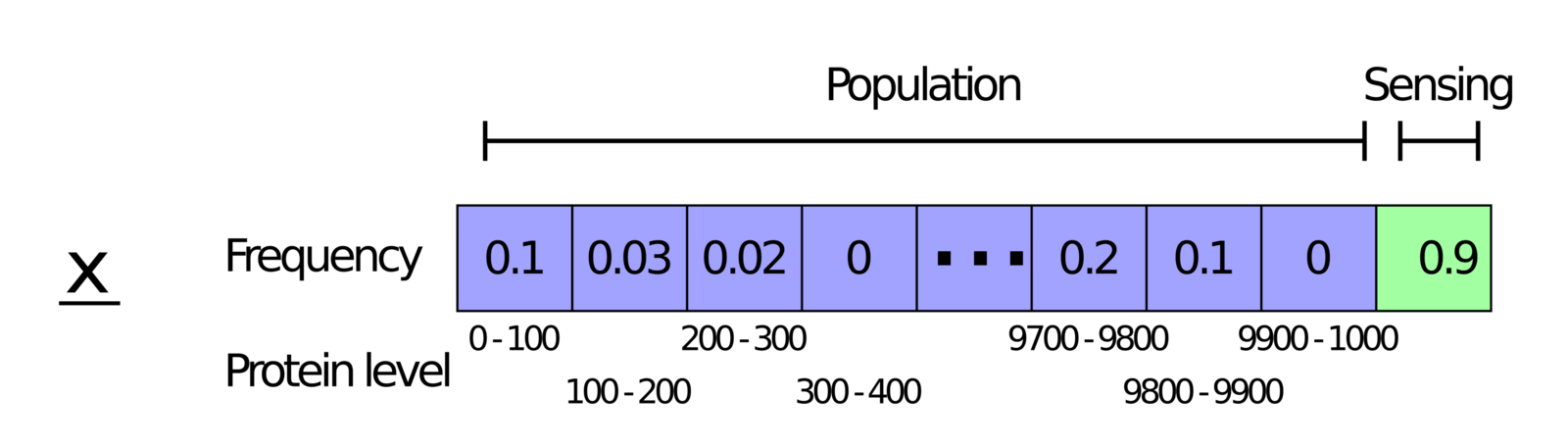
• Strategy representation 
• Fitness 
• Algorithm to optimize

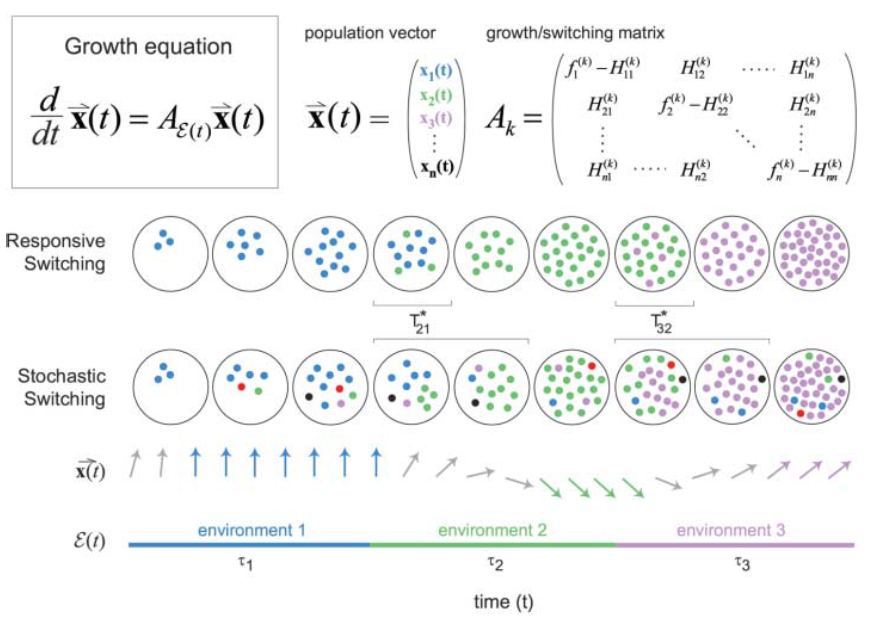
E. Kussell and S. Leibler, “Phenotypic diversity, population growth, and information in fluctuating environments.,” Science (80-. )., vol. 309, no. 5743, pp. 2075–8, Sep. 2005.

strategy: population

0

strategy

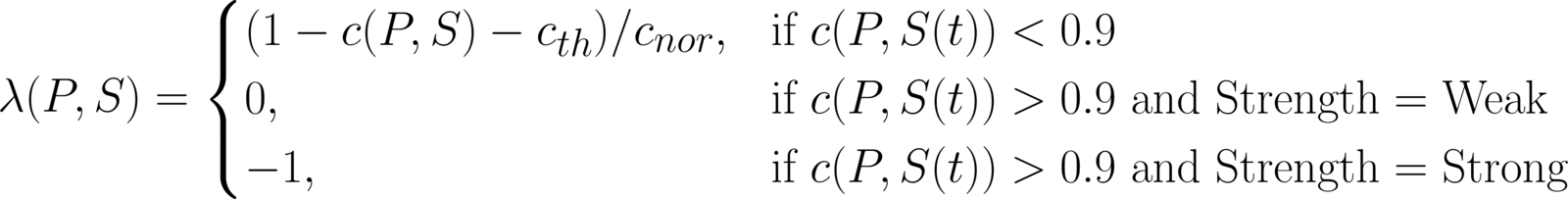
Growth rate

0

0.5

1

fitness function

Fitness

• Cells have stress response mechanisms, but are expensive. General stress responses are composed of many genes acting together and regulated by a transcription factor.
• Cost-Benefit relationship: 
  •  Cost of producing the machinery to:
    • ​Sense
    • Protect
  • Benefit of growing faster with stressor.

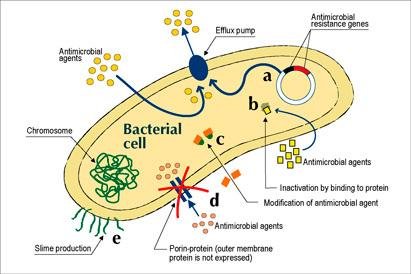
Particle swarm optimization

Each strategy is a particle.

A particle has a position, speed, inertia, information about the best strategies found by itself and its neighbors.

Parameters studied

• Cost of sensing

0 - 1 added to the cost

• Asymmetry of the environment

Symmetric

Moderately asymmetric

Highly asymmetric

Parameters studied

• Frequency of environmental transitions

1

3

10

30

100

Parameters studied

• Regularity

Periodic

Irregular

Parameters studied

• Toxicity of the stressor

Weak. Cells stop growing

Strong. Cells die

0 or -1

0.5

1

Fitness

Parameters studied

3. preliminary Results

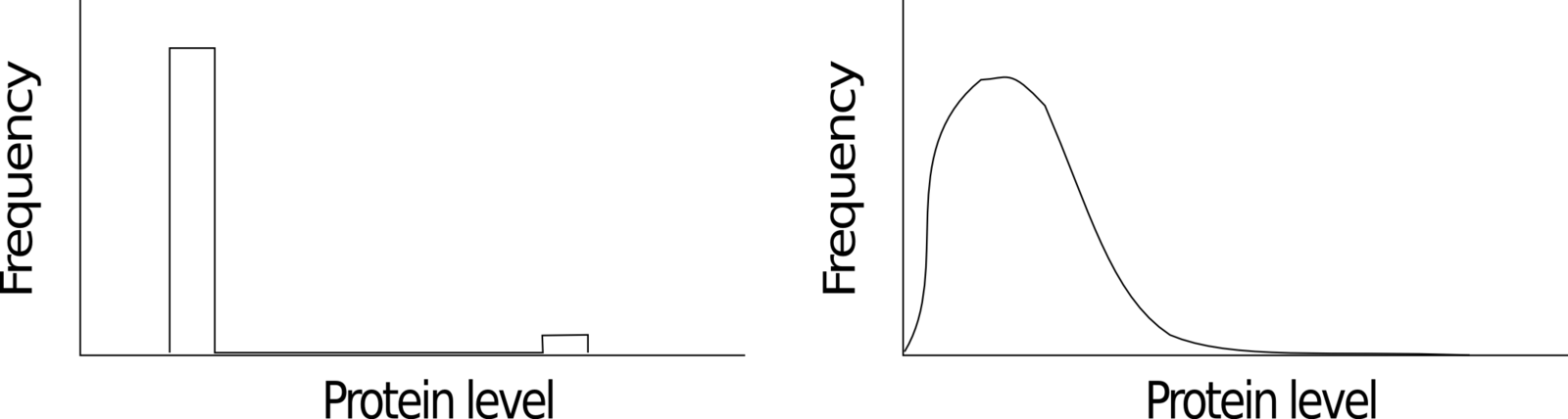
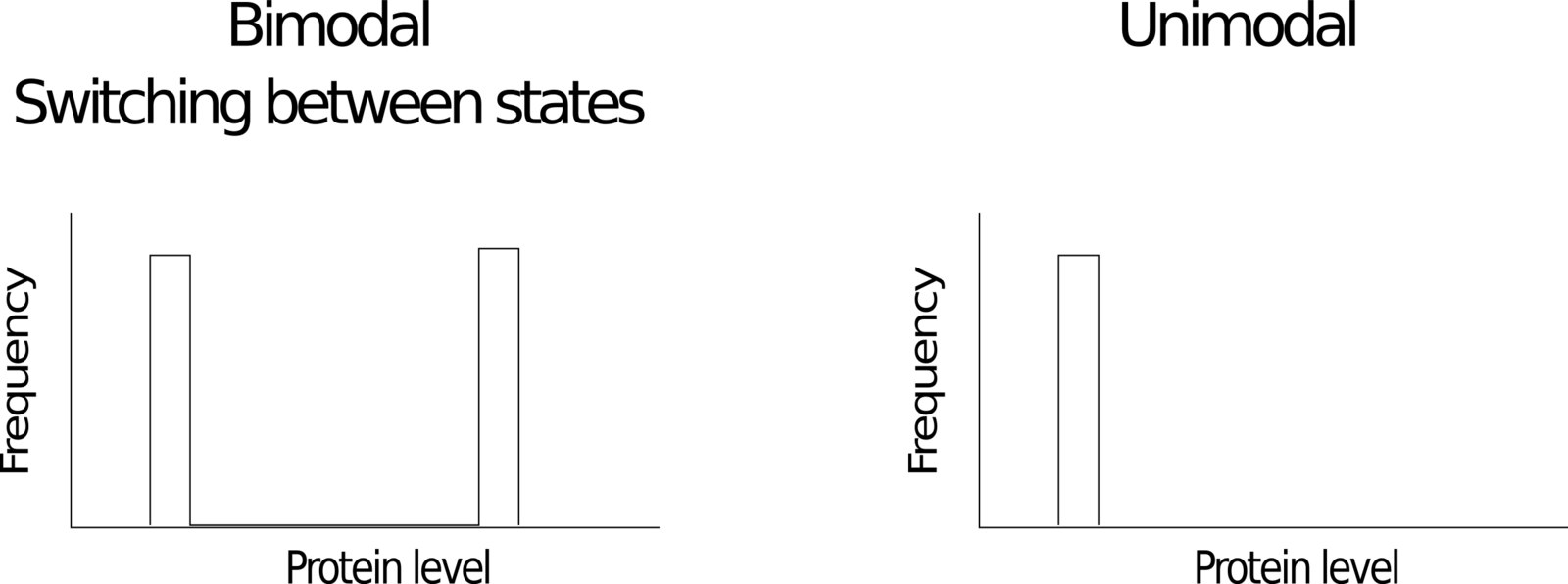
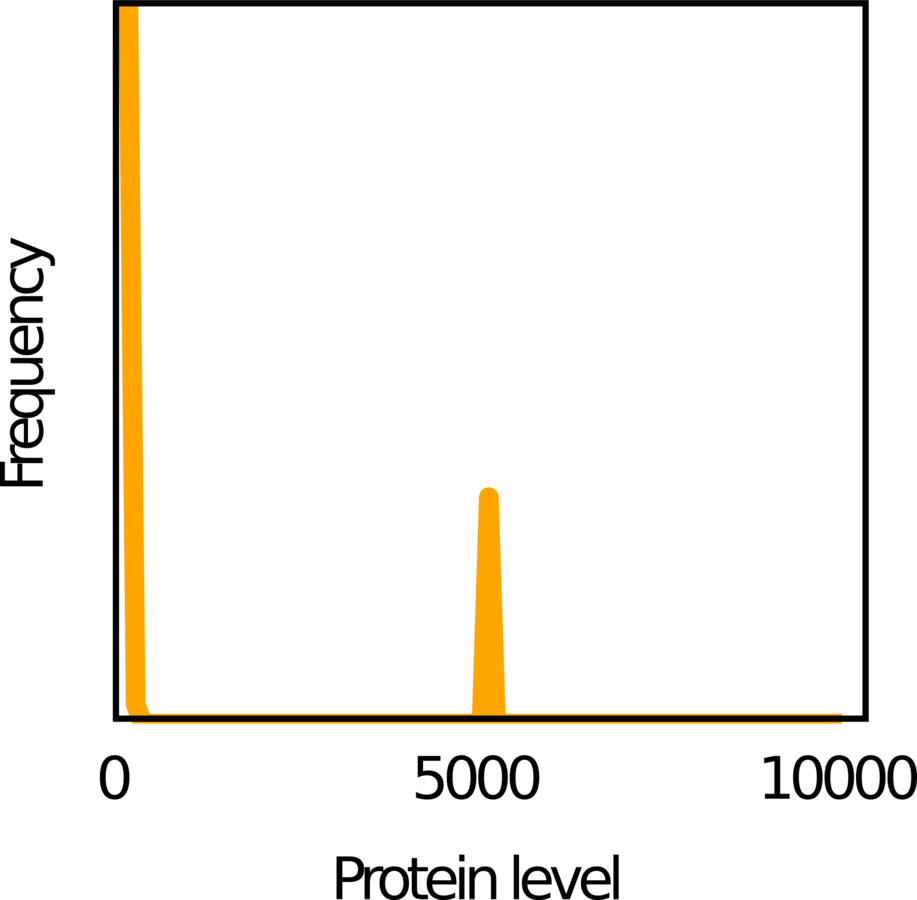
3.1 Unimodal population in fixed environments

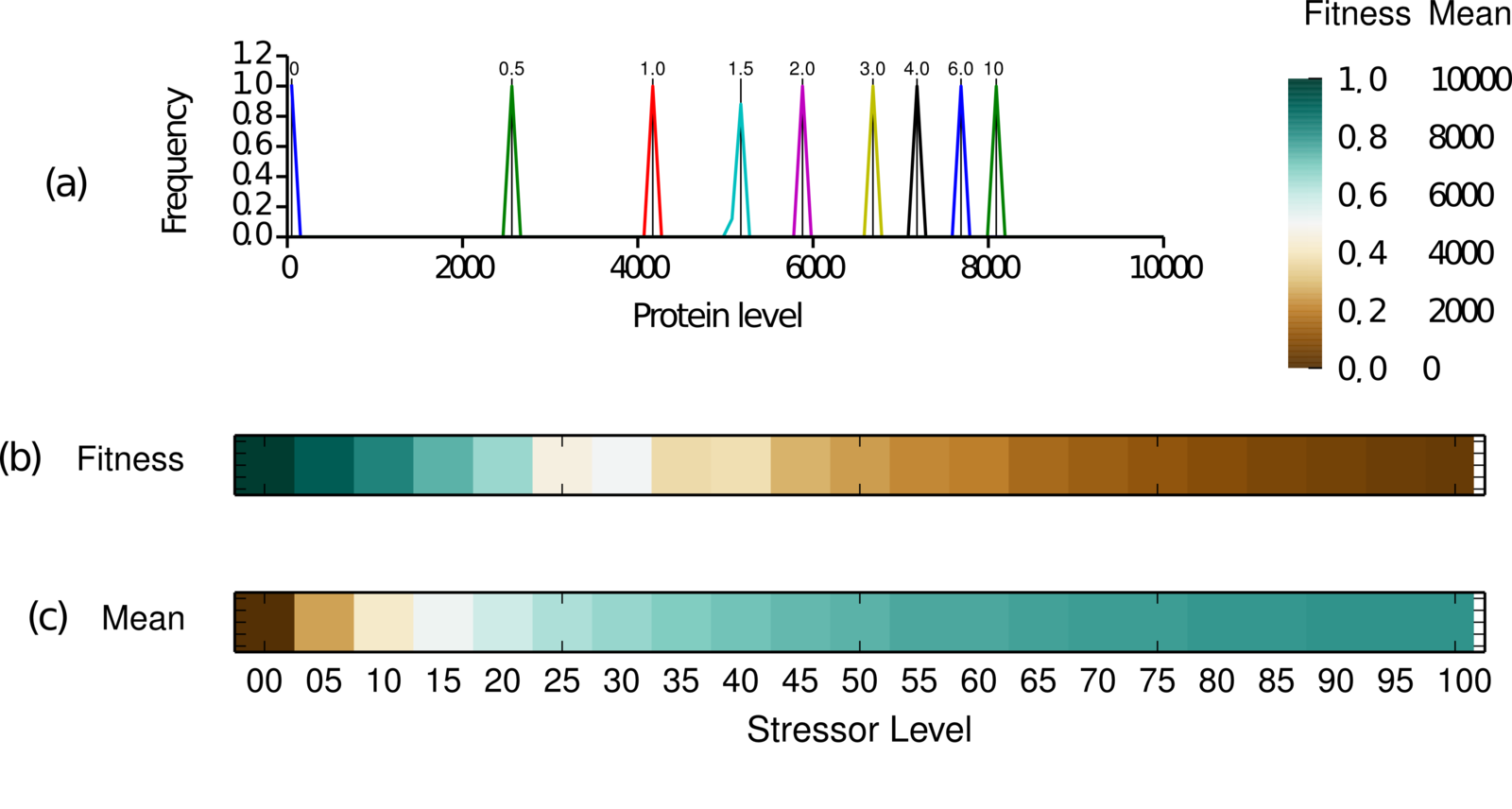
3.1 Unimodal population in fixed environments

3.1 Unimodal population in fixed environments

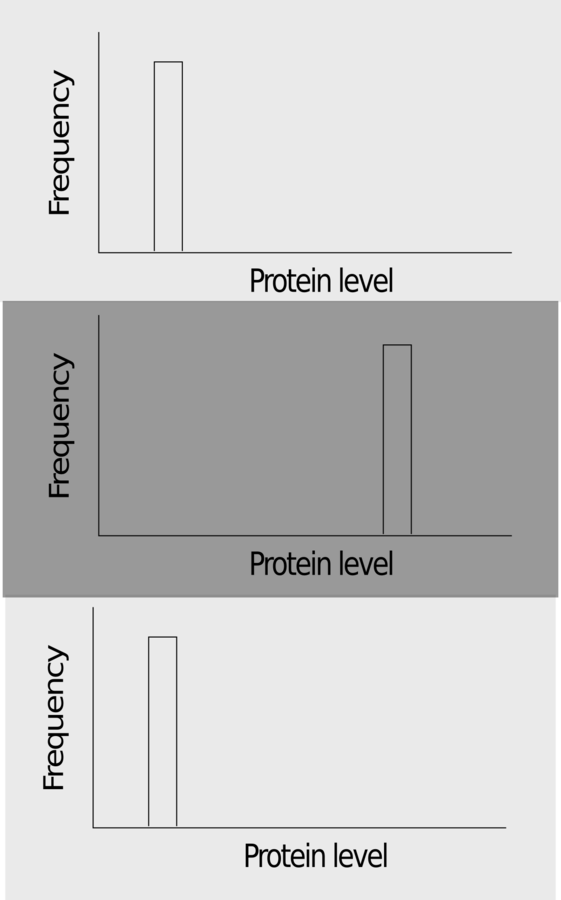
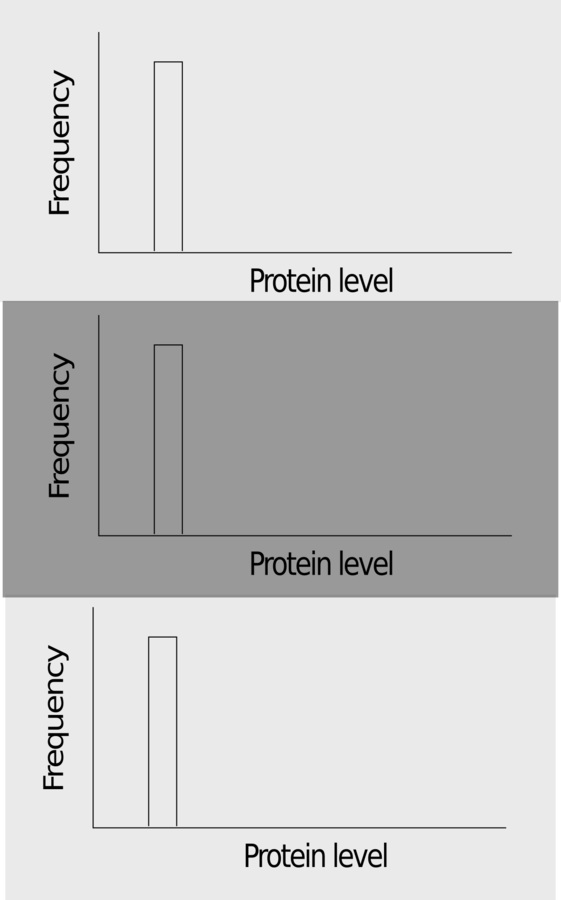
• Rapid transitions: Unimodal distribution of phenotypes adapted to the mean environment

• Intermediate range: Bimodal distribution

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

• Slow transitions: Unimodal distribution adapted to the current environment

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

3.2 Three different evolutionarily stable strategies

(Muller et al. 2013)

Asymmetric, Periodic and Strong

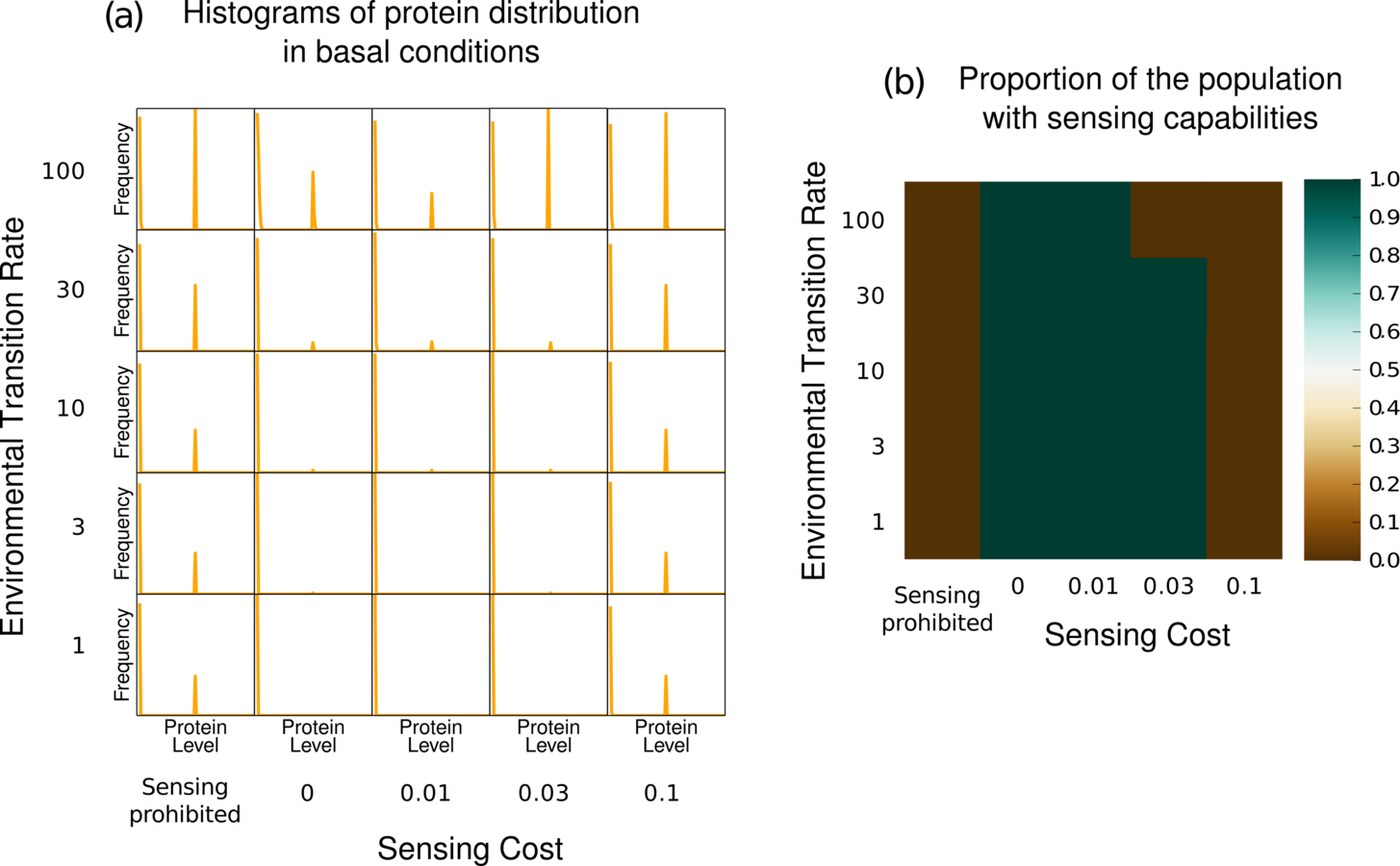
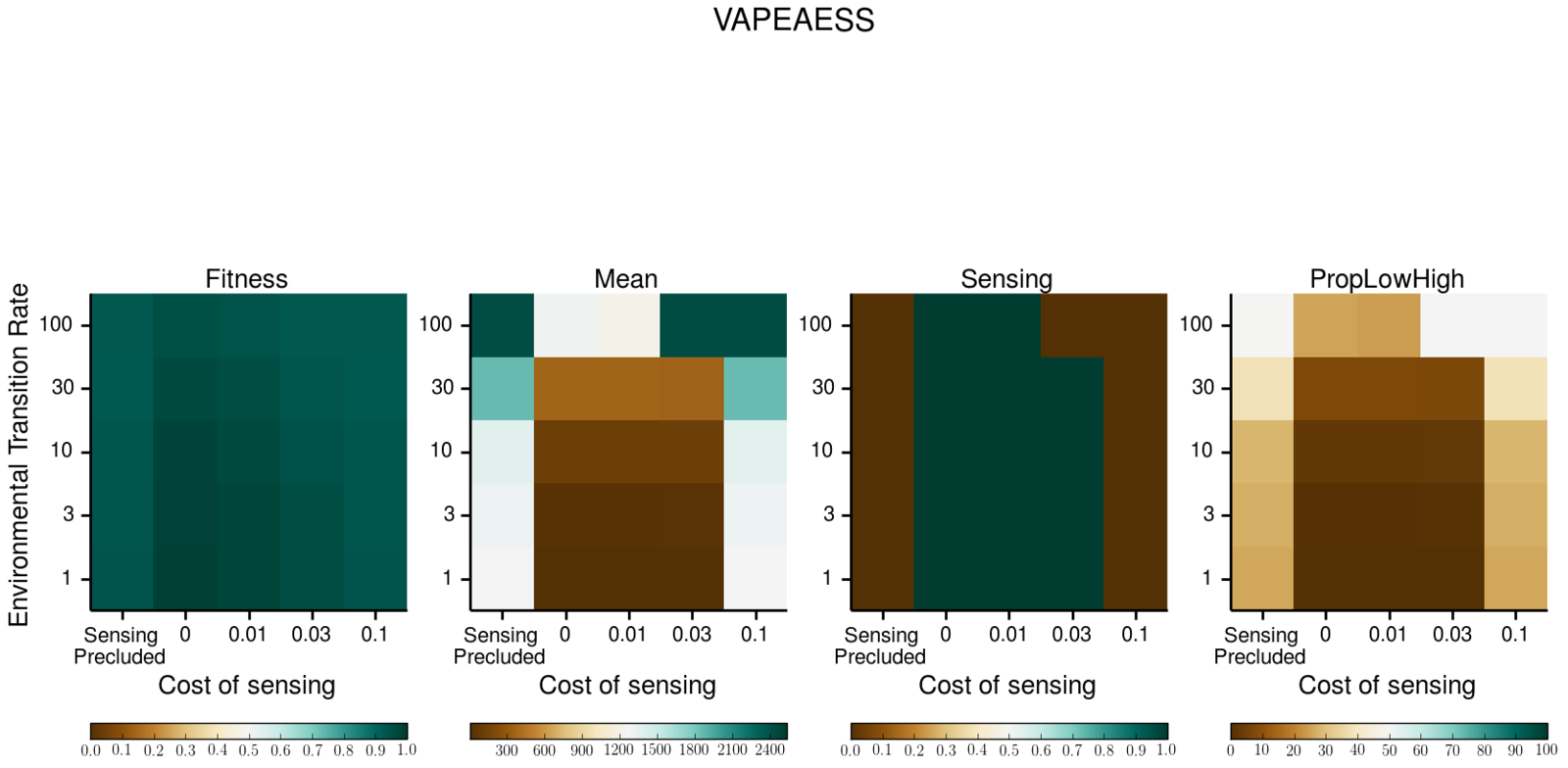
3.3 High sensing costs favour stochastic switching

(Kussell and Leibler 2005)

Asymmetric, Periodic and Strong

3.4 THE OPTIMAL CELLULAR SWITCHING RATE IS PROPORTIONAL TO THE ENVIRONMENTAL Transition RATE

1
3
10
30
100

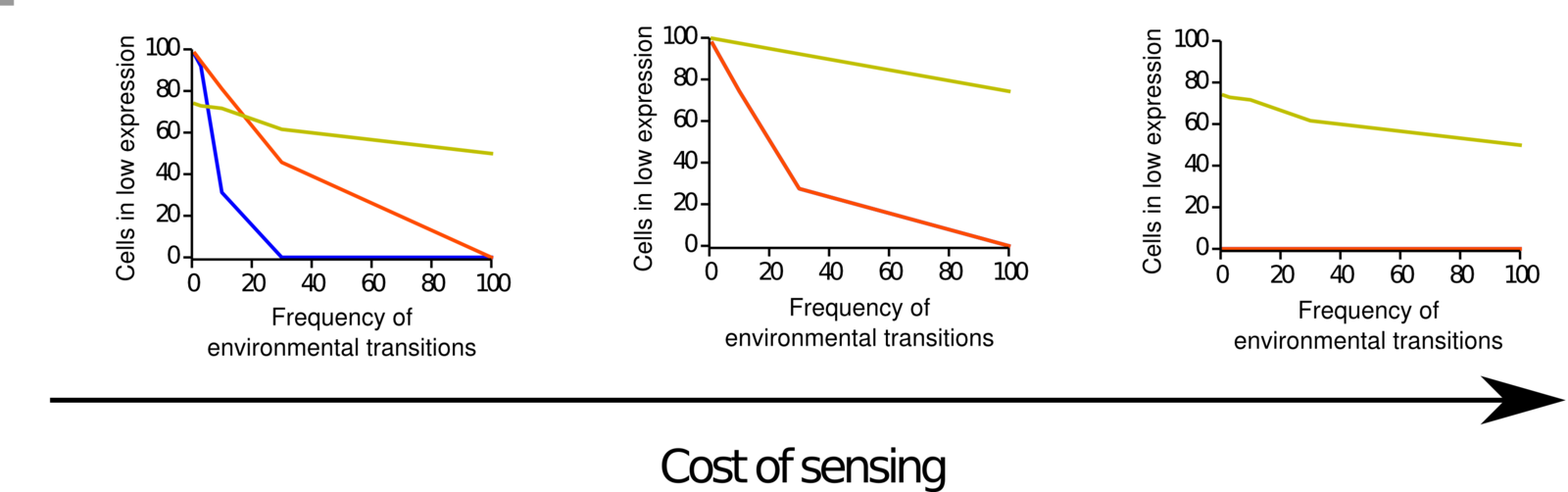
yaxis: Fraction of cells with low expression.

Lower values: Higher switching rates to the phenotype with high expression.

(Thattai and van Oudenaarden 2004)

Periodic and Strong

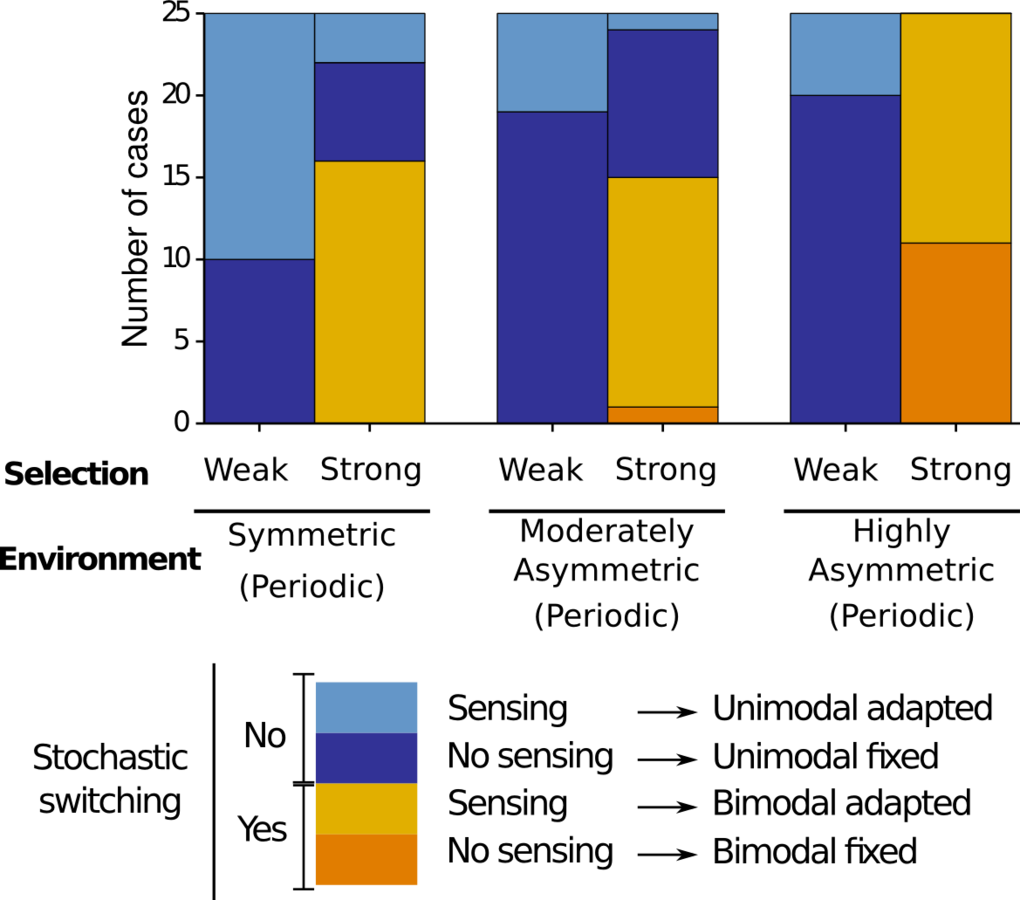
(Salathe et al. 2009)

3.5 Asymmetric fitness landscapes strongly select against stochastic switching, except when selection is very strong

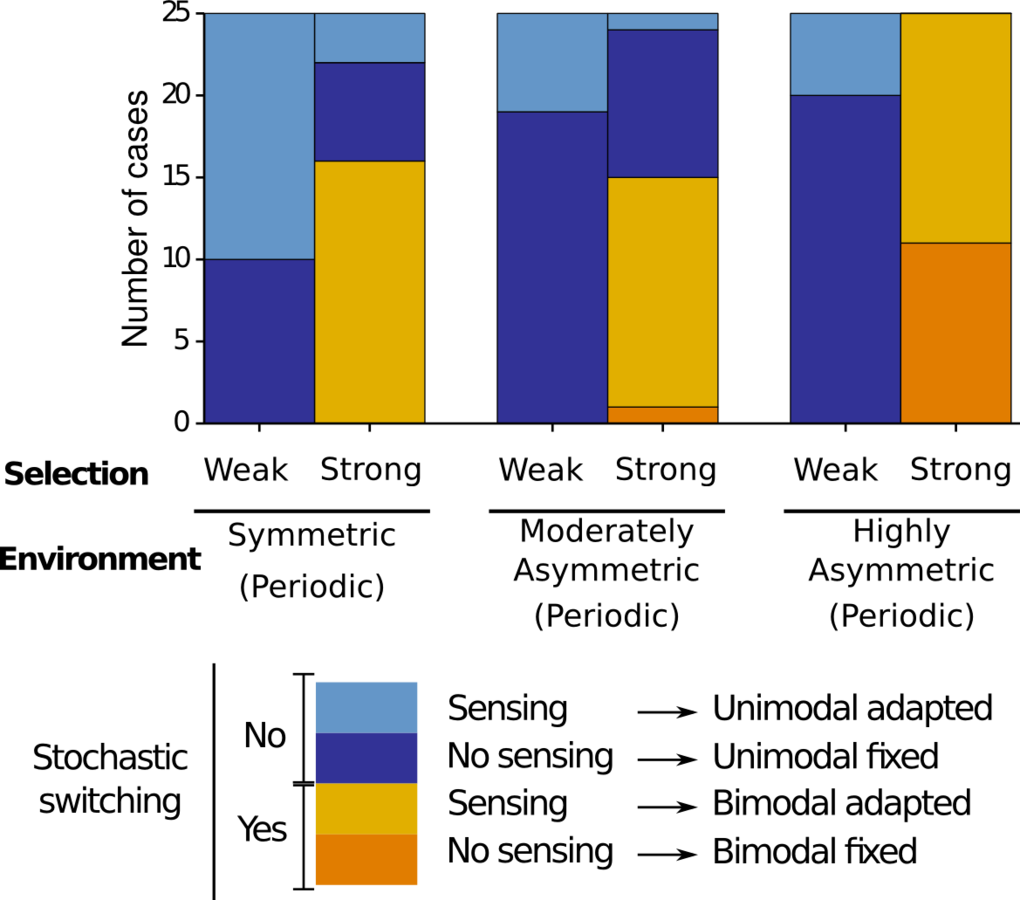
(Salathe et al. 2009)

3.5 Asymmetric fitness landscapes strongly select against stochastic switching, except when selection is very strong

3.5 Asymmetric fitness landscapes strongly select against stochastic switching, except when selection is very strong

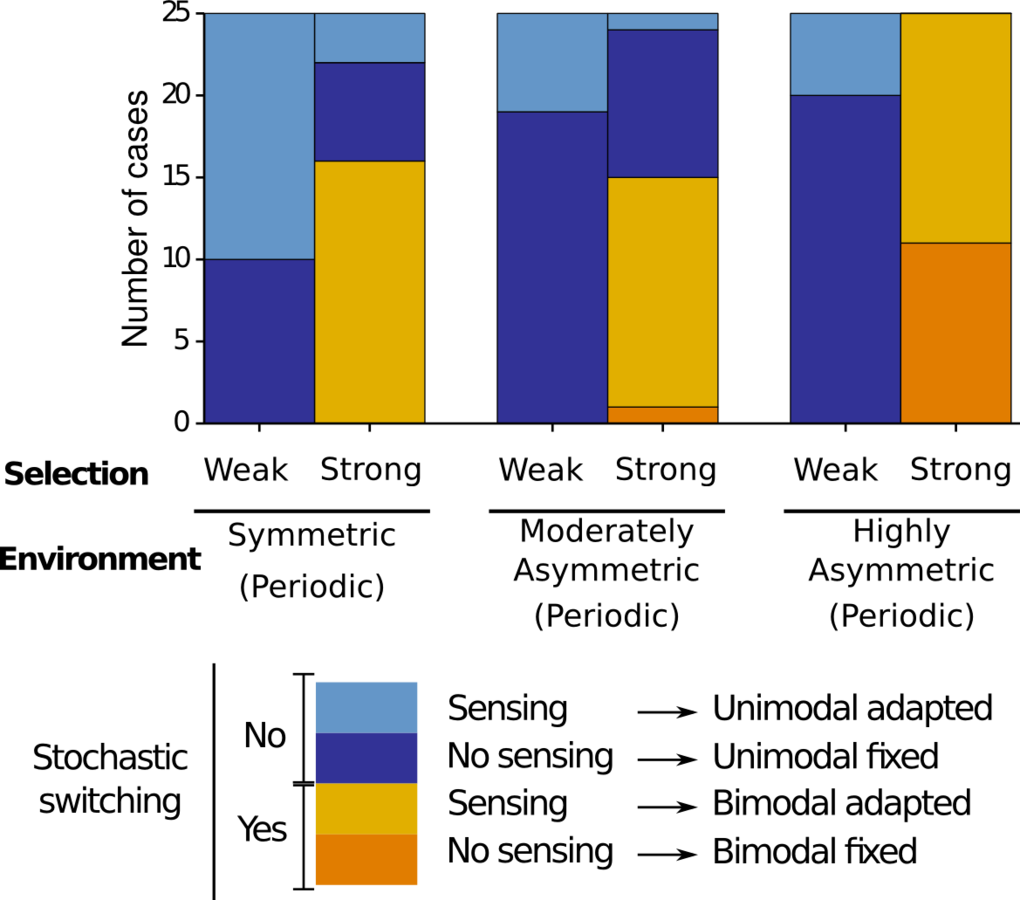
(Salathe et al. 2009)

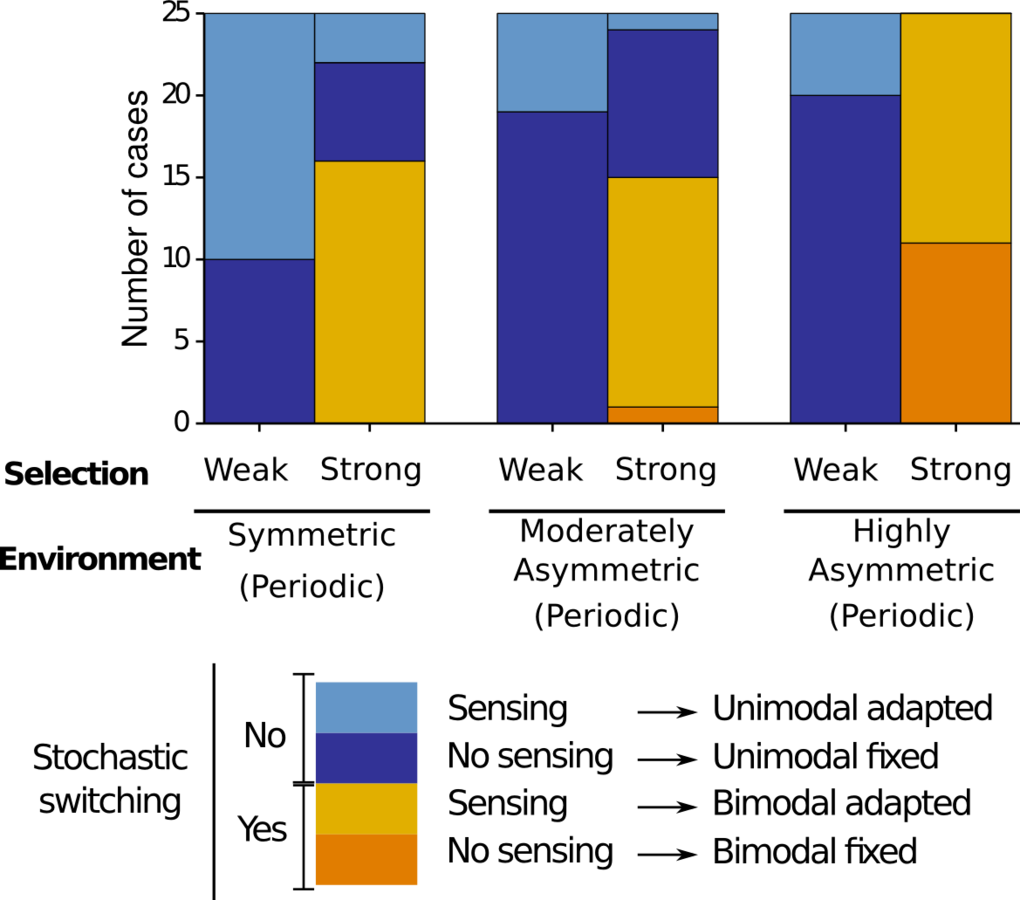
(Salathe et al. 2009)

3.5 Asymmetric fitness landscapes strongly select against stochastic switching, except when selection is very strong

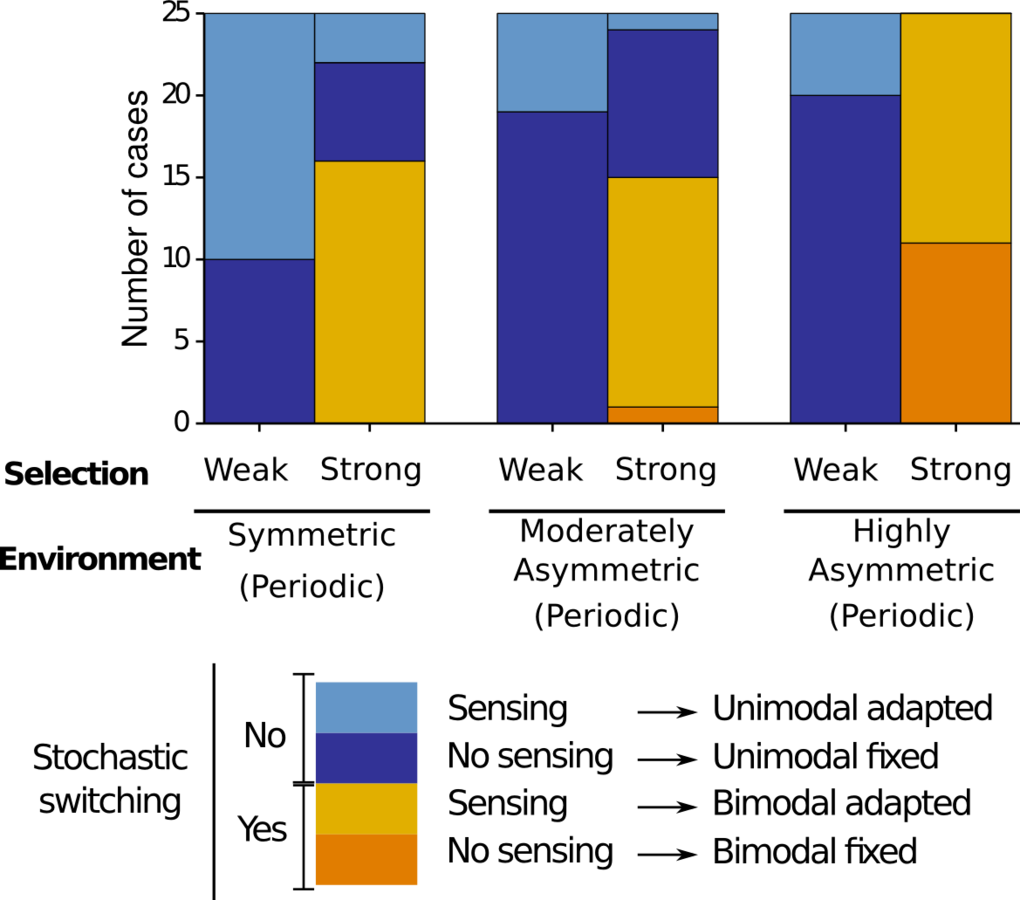
(Salathe et al. 2009)

3.5 Asymmetric fitness landscapes strongly select against stochastic switching, except when selection is very strong

4. SUMMARY

• Populations of cells can use different strategies to maximize growth in fluctuating environments.
• Sensing evolves if the cost of sensing is lower than the cost of being maladapted in the second environment.
• The optimal strategy is determined by the cost of sensing, the time spent at each environment state, the frequency of environmental transitions and the toxicity of the stressor.
• High sensing costs, strong selection by the toxic and asymmetric environments favor stochastic switching.

5. GOALS

1. Hypothesis: Continuous phenotype vs Multistability
2. Add information about environment

GOal 1. multimodal vs continuous

• When only two environmental states are accessible, the population converges to unimodal or bimodal distributions.
• ​With many environmental states, the optimal strategy may be multimodal.
• ​However, multimodal networks are large, hard to evolve and hard to maintain when the environment changes. ​Maybe a phenotype continuous can be beneficial in those conditions.

GOal 1. multimodal vs continuous

• When only two environmental states are accessible, the population converges to unimodal or bimodal distributions.
• ​With many environmental states, the optimal strategy may be multimodal.
• ​However, multimodal networks are large, hard to evolve and hard to maintain when the environment changes. ​Maybe a phenotype continuous can be beneficial in those conditions.

STEPS:

1. Establish a measure that distinguish mulstistability from a phenotype continuous. 

GOal 1. multimodal vs continuous

• When only two environmental states are accessible, the population converges to unimodal or bimodal distributions.
• ​With many environmental states, the optimal strategy may be multimodal.
• ​However, multimodal networks are large, hard to evolve and hard to maintain when the environment changes. ​Maybe a phenotype continuous can be beneficial in those conditions.

STEPS:

1. Establish a measure that distinguish mulstistability from a phenotype continuous. 
2. Add some cost if a phenotype continuous is not evolved. Calculate the minimum cost needed to evolve a phenotype continuous.

GOal 1. multimodal vs continuous

• When only two environmental states are accessible, the population converges to unimodal or bimodal distributions.
• ​With many environmental states, the optimal strategy may be multimodal.
• ​However, multimodal networks are large, hard to evolve and hard to maintain when the environment changes. ​Maybe a phenotype continuous can be beneficial in those conditions.

STEPS:

1. Establish a measure that distinguish mulstistability from a phenotype continuous. 
2. Add some cost if that if a phenotype continuous is not evolved, calculate the minimum cost needed to evolve a phenotype continuous.
3. Increase the number of environments measuring the minimum cost.

GOal 1. multimodal vs continuous

• When only two environmental states are accessible, the population converges to unimodal or bimodal distributions.
• ​With many environmental states, the optimal strategy may be multimodal.
• ​However, multimodal networks are large, hard to evolve and hard to maintain when the environment changes. ​Maybe a phenotype continuous can be beneficial in those conditions.

STEPS:

1. Establish a measure that distinguish mulstistability from a phenotype continuous. 
2. Add some cost if that if a phenotype continuous is not evolved, calculate the minimum cost needed to evolve a phenotype continuous.
3. Increase the number of environments measuring the minimum cost.
4. Check hypothesis: This cost will decrease with the number of environments.

• Challenges:
  • How to quantify a phenotype continuous.
    • Phenotypes need to be connected and frequency in consecutive protein levels cannot increase too fast.
  • Number of conditions increases exponentially.
    • How to summarize the results.
  • Time for convergence will probably be larger.

GOal 1. multimodal vs continuous

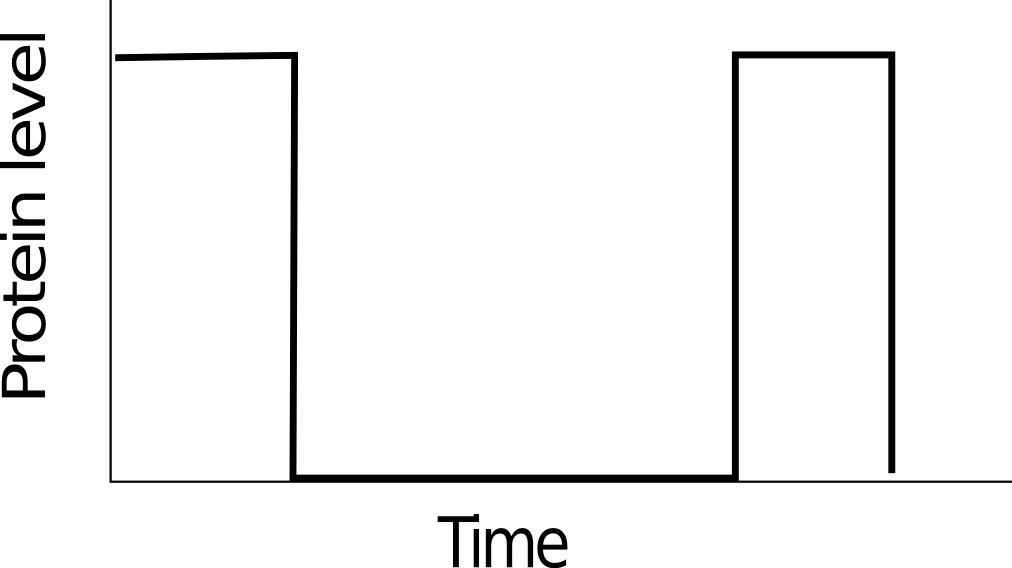
goal 2. Add dynamics

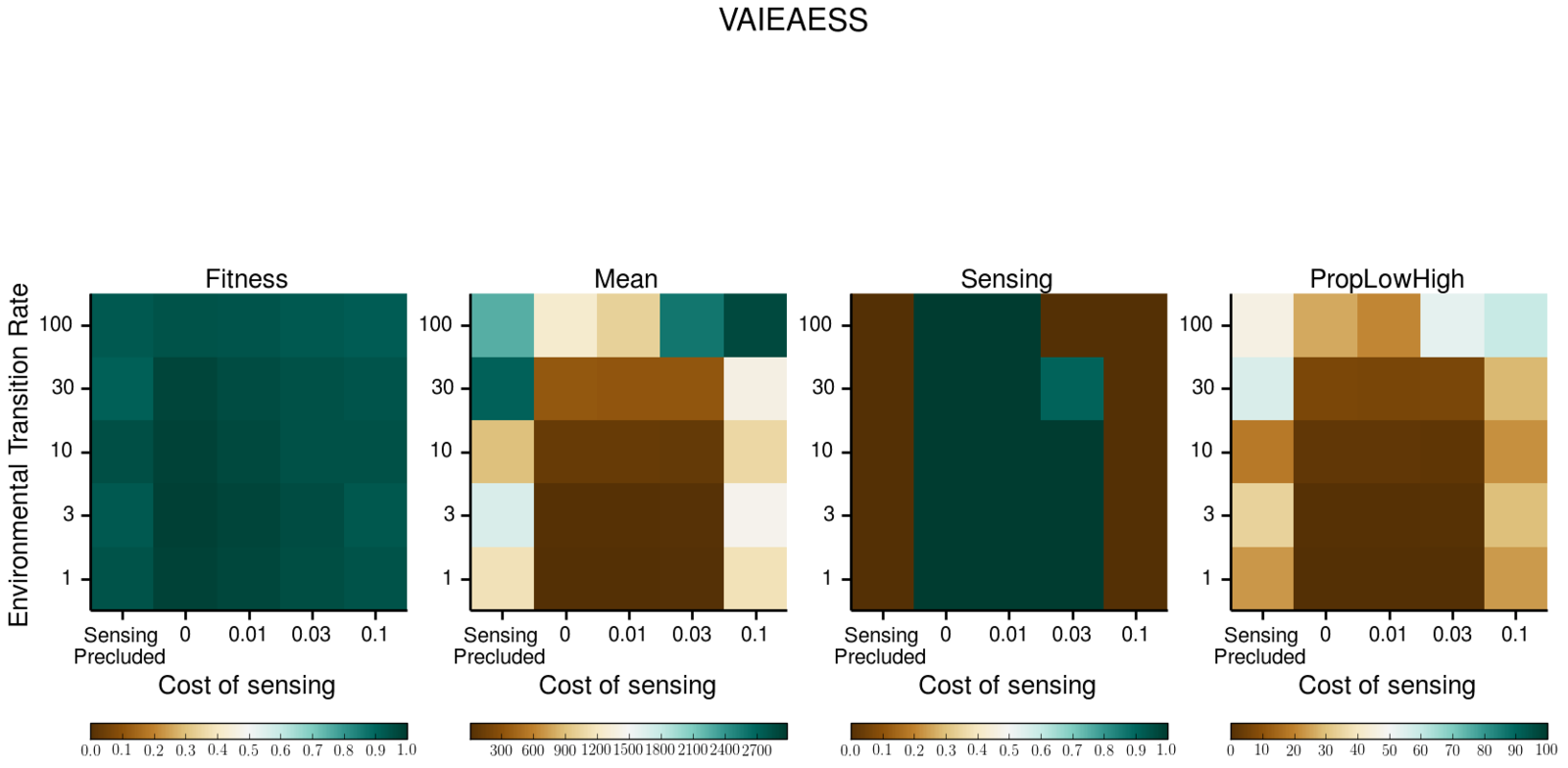
Periodic

Irregular

Thanks everybody!