distributions of phenotypes
in fluctuating environments
Javier Garcia-Bernardo
Advisor: Dr. Mary Dunlop
February 6th, 2015

1. Introduction
1.1 fluctuating environments
Cells need to continuously adapt to an uncertain environment.

1.1 fluctuating environments
Cells need to continuously adapt to an uncertain environment.

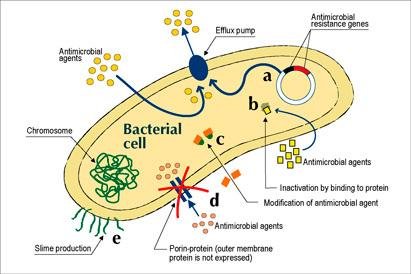
- Cells have stress response mechanisms, but are expensive. General stress responses are composed of many genes acting together and regulated by a transcription factor.
-
Cost-Benefit relationship:
-
Cost of producing the machinery to:
- Sense
- Protect
- Benefit of growing faster with stressor.
-
Cost of producing the machinery to:
1.1 fluctuating environments
Cells need to continuously adapt to an uncertain environment.
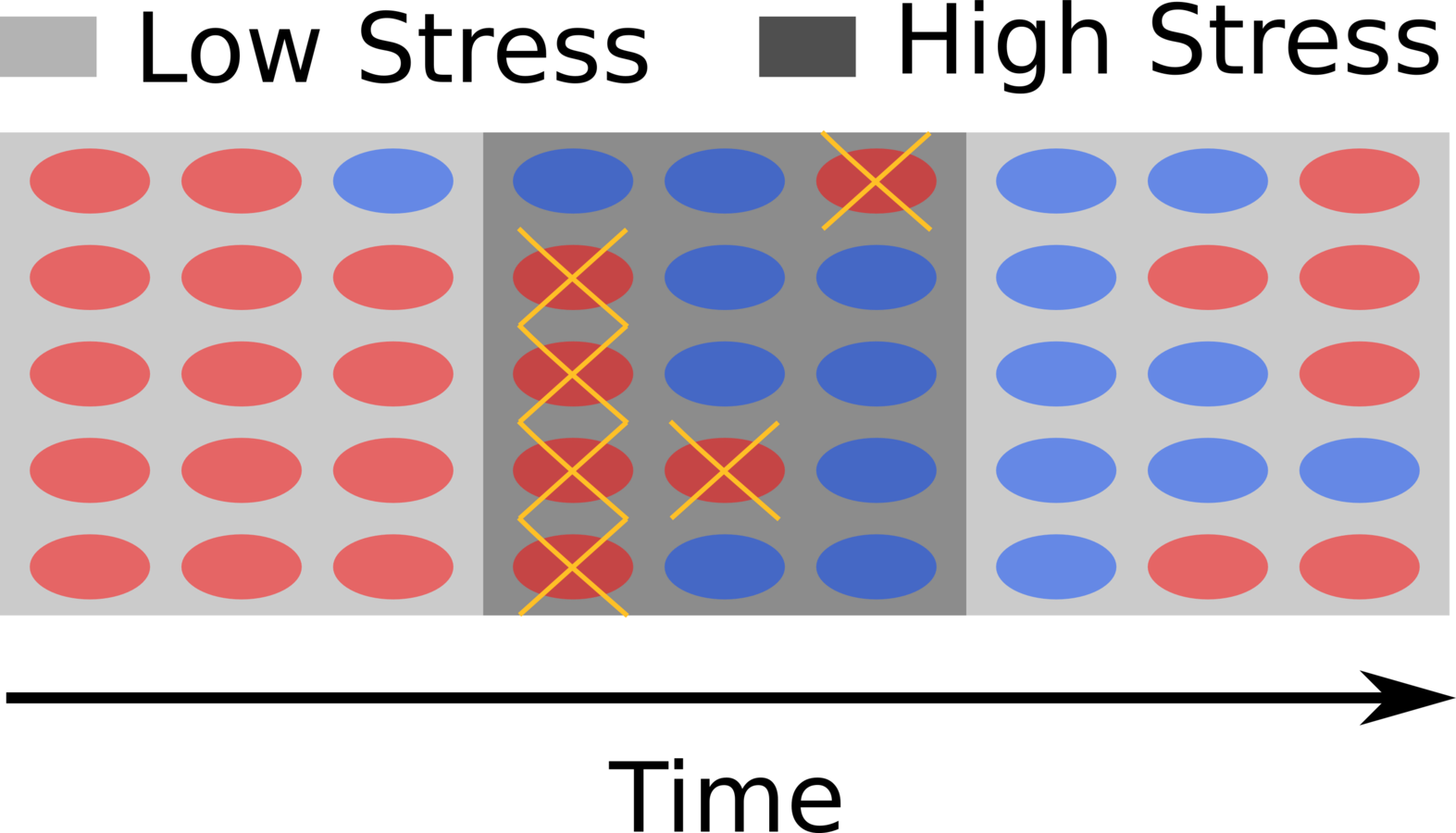
Examples of phenotypic diversity:
Delayed germination of seeds
Noise in genetic networks increase antibiotic resistance
- Cells have stress response mechanisms, but are expensive. General stress responses are composed of many genes acting together and regulated by a transcription factor.
-
Cost-Benefit relationship:
-
Cost of producing the machinery to:
- Sense
- Protect
- Benefit of growing faster with stressor.
-
Cost of producing the machinery to:
1.1 fluctuating environments
Cells need to continuously adapt to an uncertain environment.

1.2 what is the problem
Multistability is not too common in bacteria. Examples:
- Stress response (persistance)
- Carbon intake (diauxic growth)
What are the results?
- We proof our method works by replicating the results of other papers.
- We use our method to show that multistability is not better when the environment is noisy or composed of many states.
- Therefore, the surprising story is that multistability is even evolved. However, this can be evolved by accounting for increased autocorrelation times.
Multistability is harder to evolve and maintain, since it requires a genetic network. But it seems like the optimal strategy (why would you bother on having intermediate phenotypes).
1.3 What has been done
Dr. Richard Levins (1930-).
Evolution in Changing Environments, 1968
Analytic and in vivo experiments with two phenotypes and two environments.
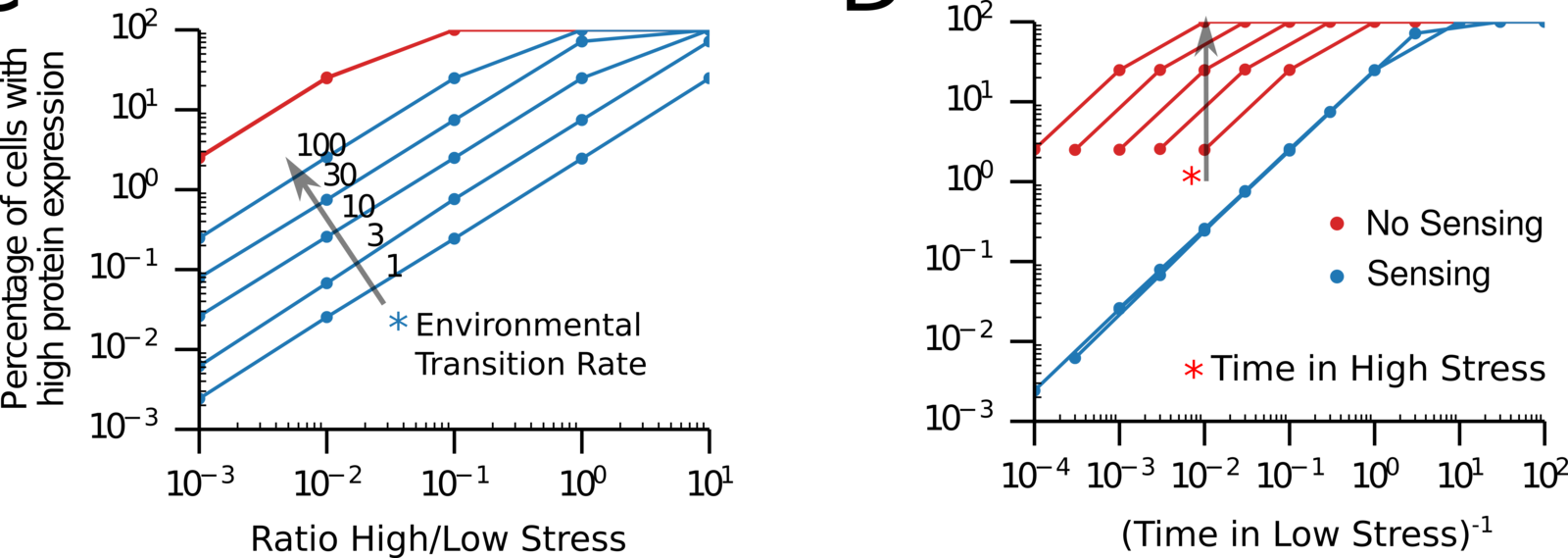
The optimal strategy depends on:
- Cost of sensing.
- Time spent at each environmental state.
- Frequency of environmental transitions.
- Growth rate of each phenotype in the two environment states.
- Information about future conditions.
Text

Acar and van Oudenaarden (Nature, 2008)
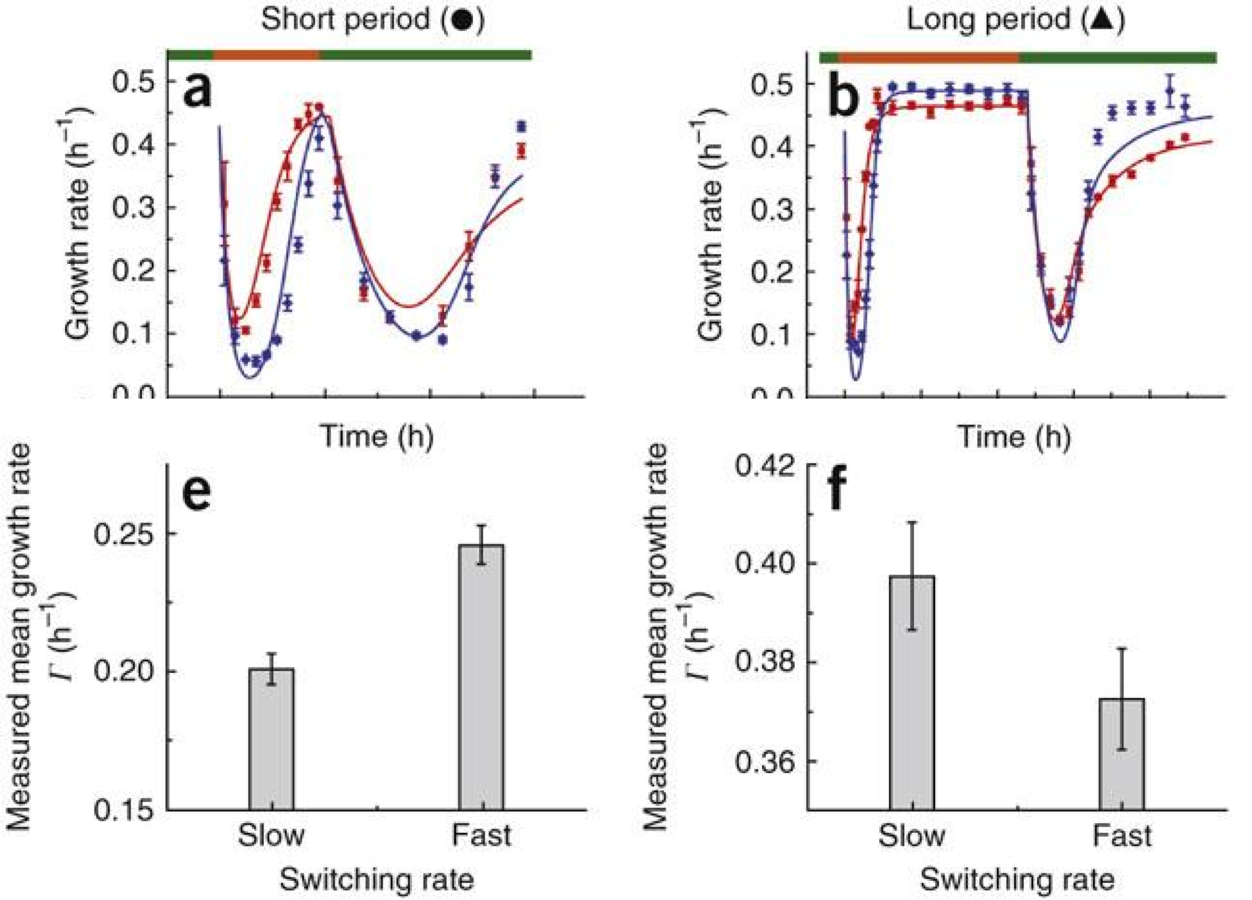
Population of cells with fast switching rates between phenotypes have higher growth rates in environments with fast transitions between states.
Population of cells with slow switching rates between phenotypes have higher growth rates in environments with slow transitions between states.
1.4 OuR approach
-
Use evolutionary algorithms to find optimal strategies of growth in fluctuating environments.
- Analytic/Numeric solutions are not easy when sensing is allowed and the number of environment increases.
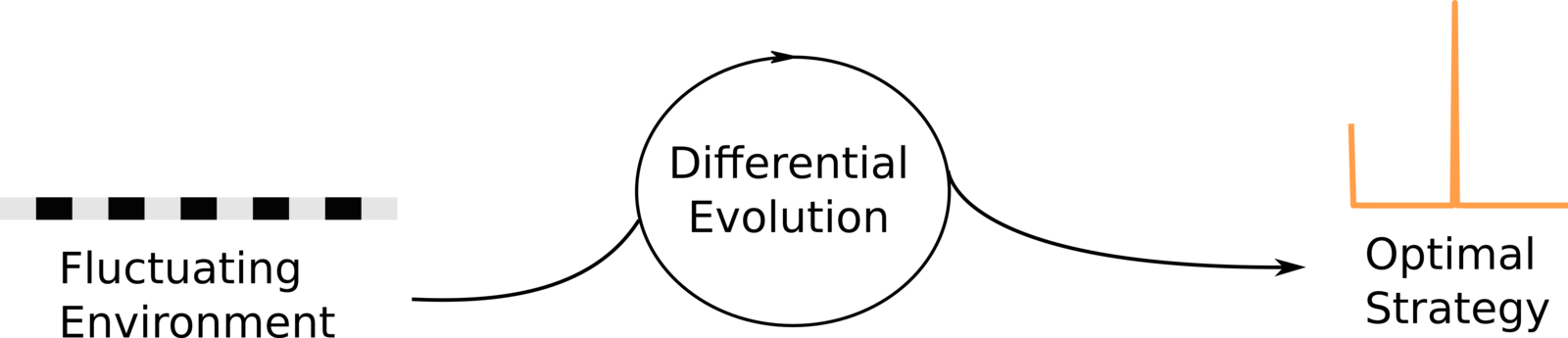
The best known equilibrium in biology is known as the evolutionarily stable strategy (ESS), first introduced in (Smith & Price 1973).
2. EVOLUTION OF STRATEGIES
2.1 Environment representation
2.2 Strategy representation
2.3 Fitness
2.4 Algorithm to optimize
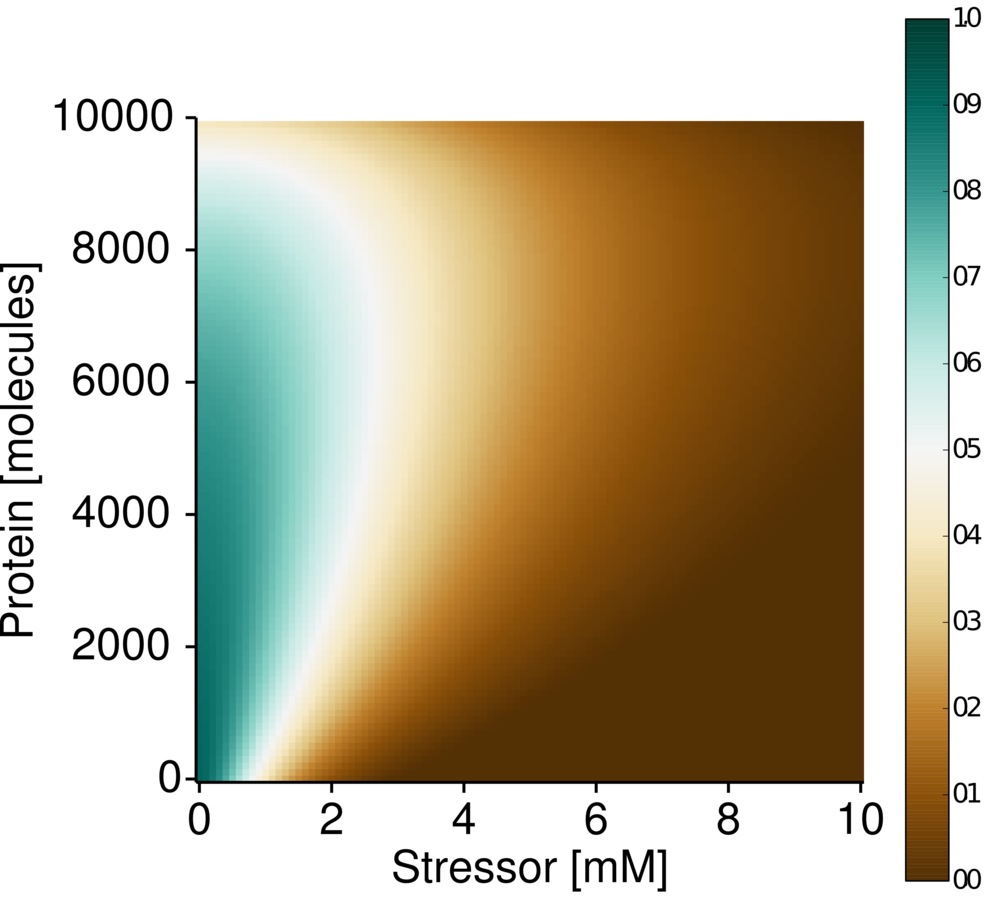
2.1 environment
Concentration of the stressor.
Parameter: Cost of sensing
0 - 1 added to the cost
2.1 environment
Concentration of the stressor.
Parameter: Asymmetry of the environment
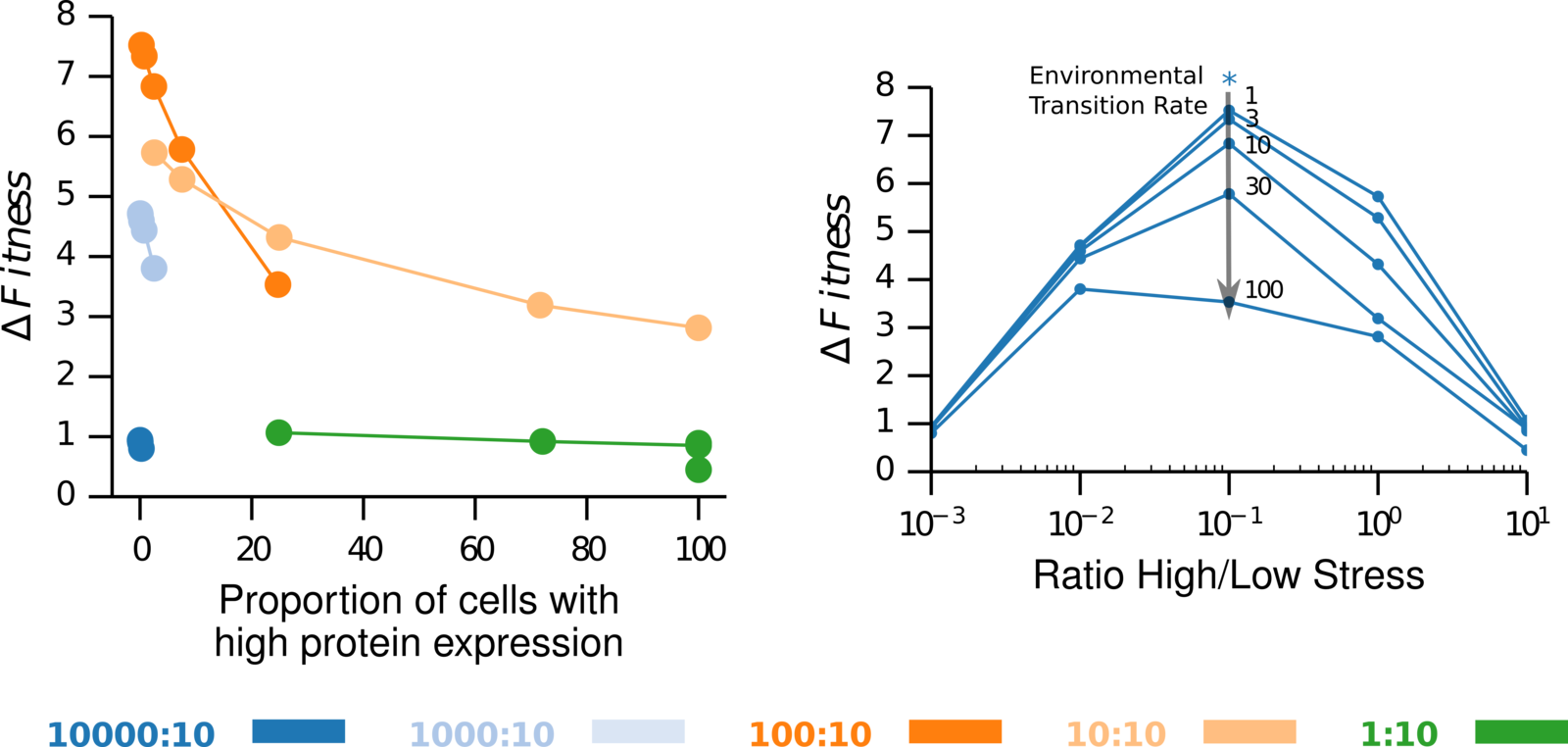
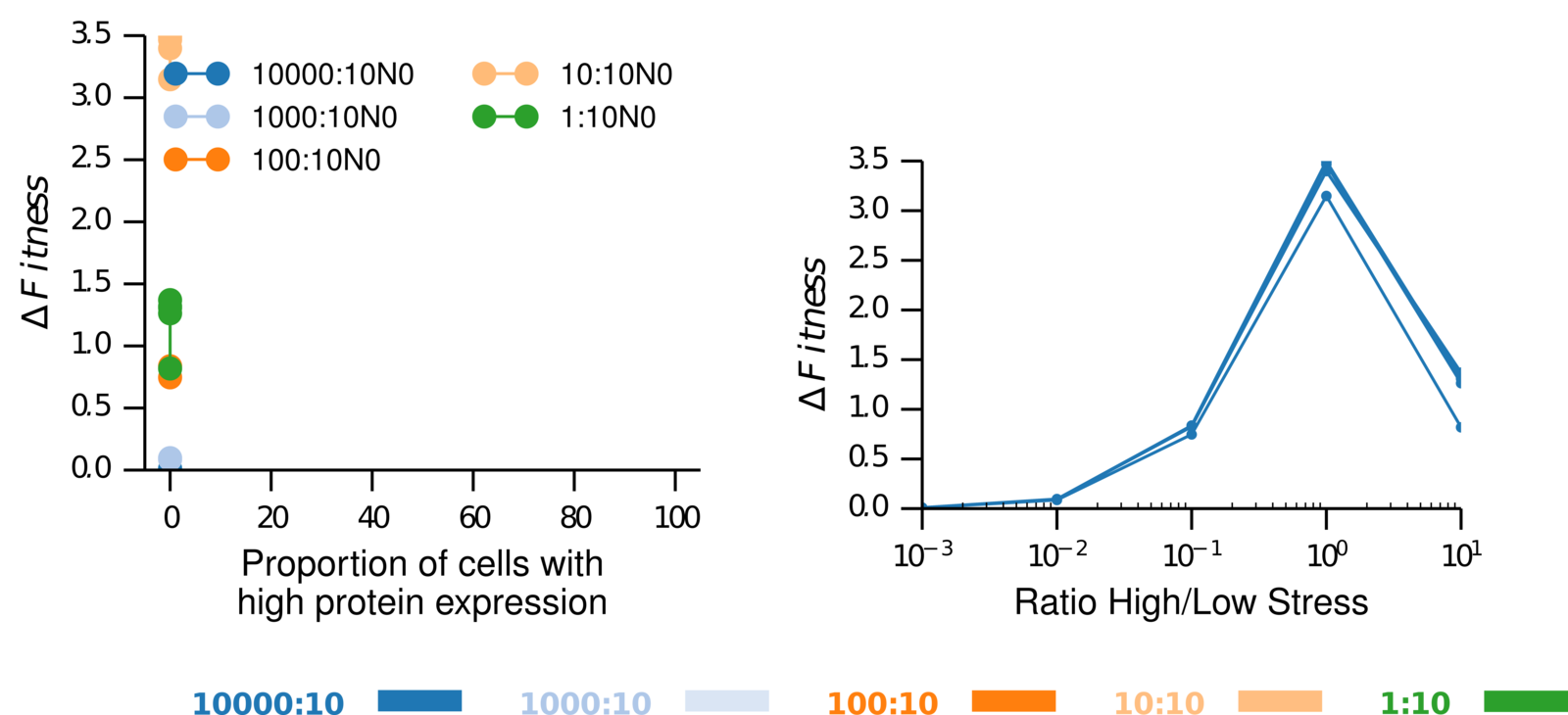
1:10
10:10
100:10
1000:10
10000:10

2.1 environment
Concentration of the stressor.
Parameter: Frequency of environmental transitions
1
3
10
30
100

2.1 environment
Concentration of the stressor.
Parameter: Toxicity of the stressor
Weak. Cells stop growing
Strong. Cells die
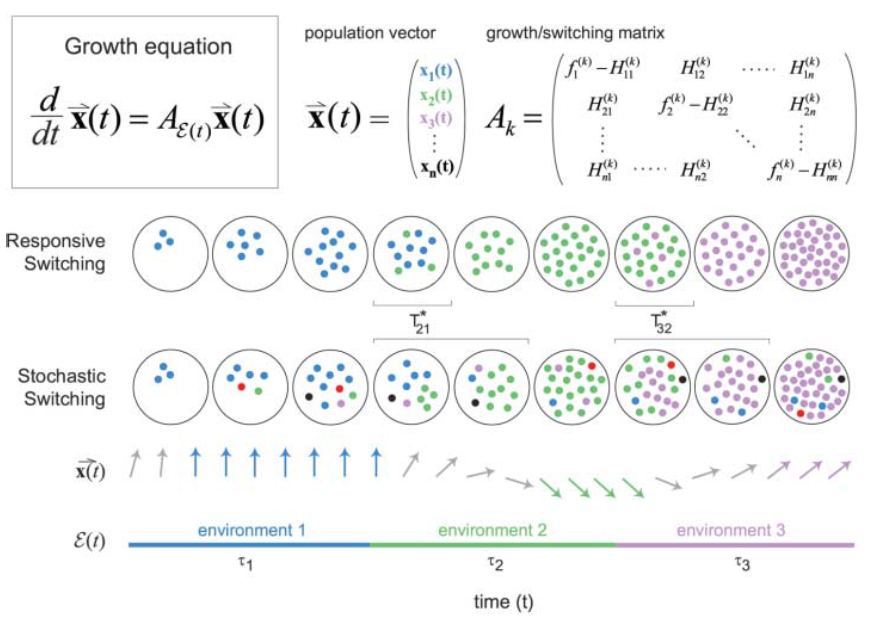
E. Kussell and S. Leibler, “Phenotypic diversity, population growth, and information in fluctuating environments.,” Science (80-. )., vol. 309, no. 5743, pp. 2075–8, Sep. 2005.
2.2 strategy: population
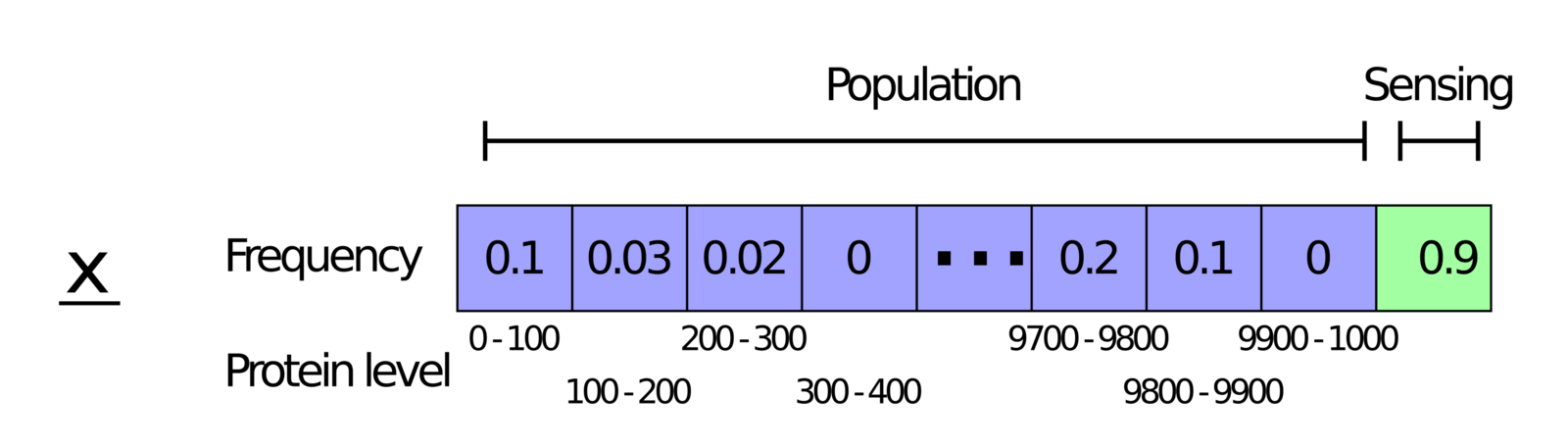
0
2.2 strategy
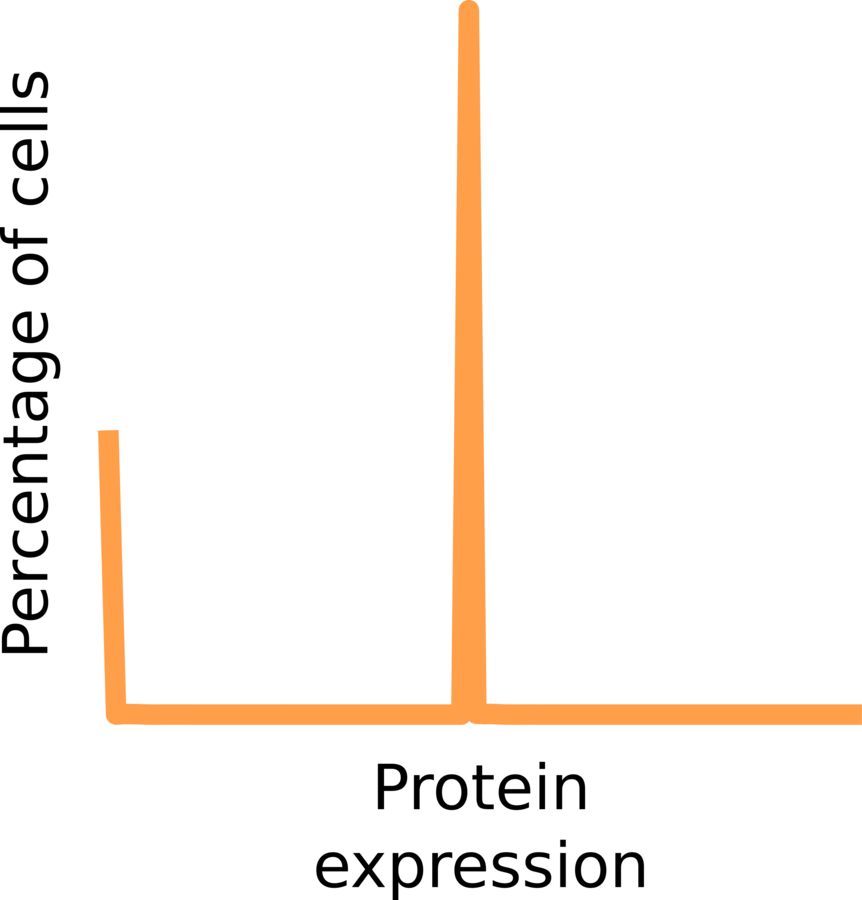

0
2.2 strategy
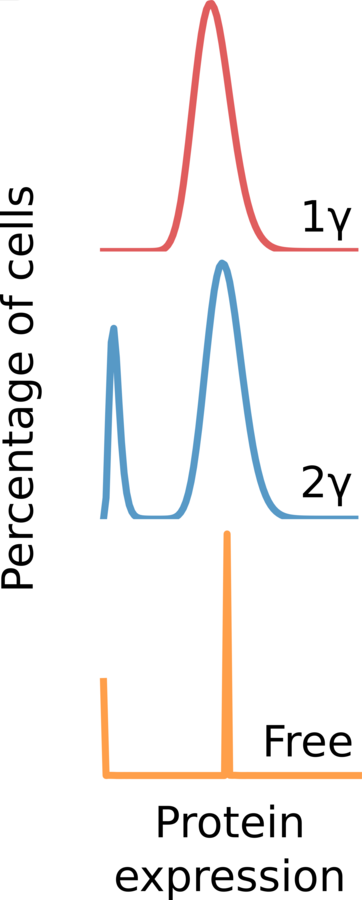
1 GAMMA: 2 + 1 parameter

0
2.2 strategy
2 GAMMA: 6 + 1 parameter


0
2.2 strategy
FREE: 100 + 1 parameter

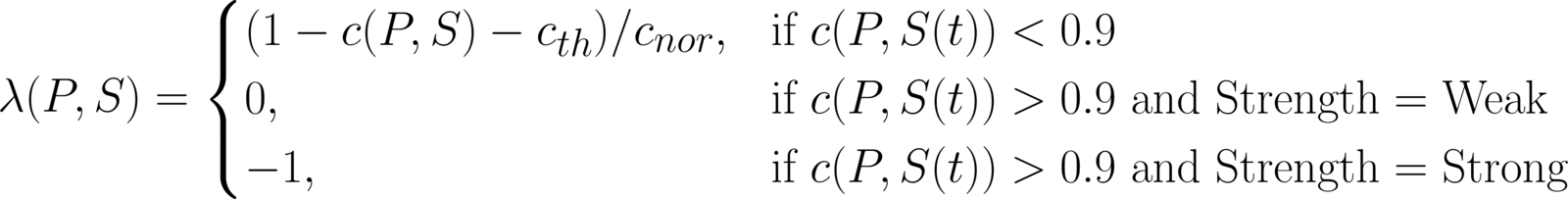
Geometric growth rate
0.5
1
2.3 fitness function
Fitness
0 or -1
2.4 Algorithm: Differential evolution
Each strategy is a vector.
Vectors are combined:
3. Results
3.1 weak selection hinders multistability
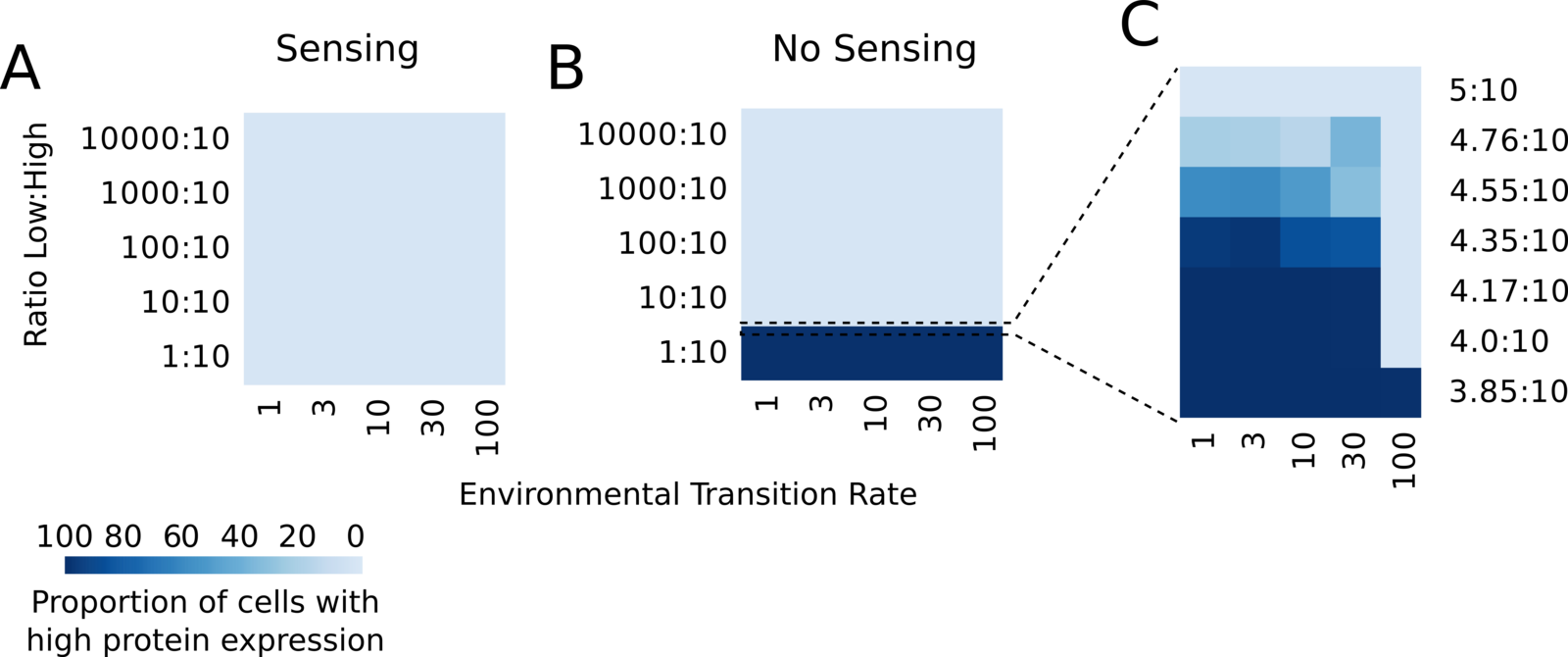
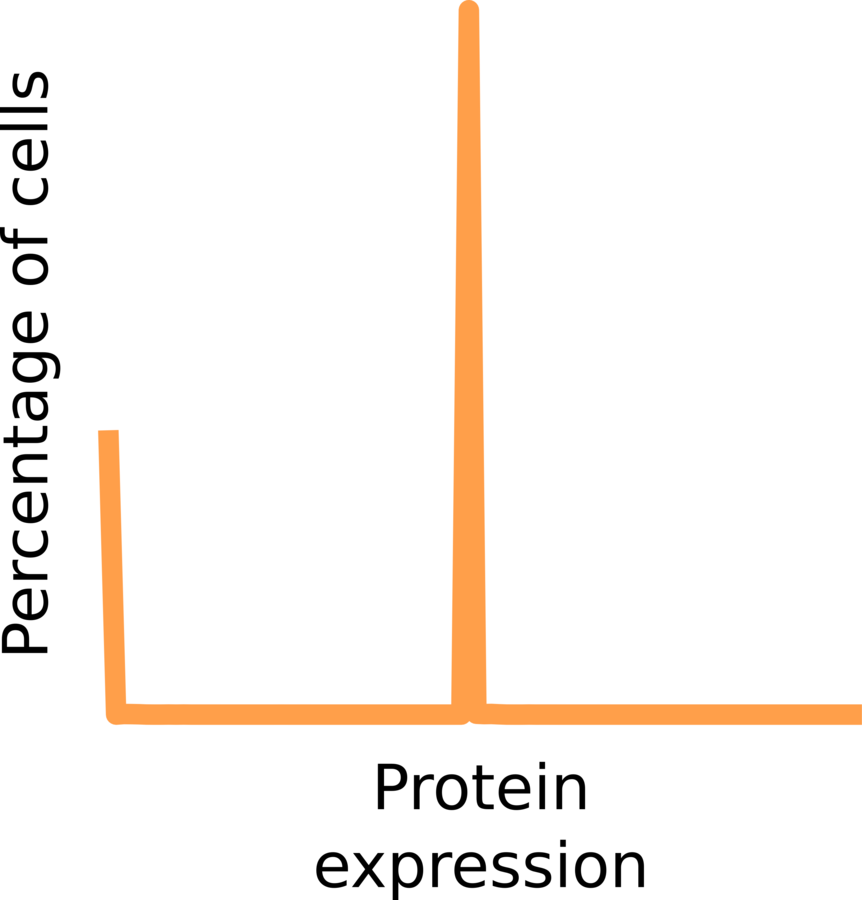
3.2 multistability is favoured in strong envs

3.3 relation sensing and ratio low:high stress
3.3 Gamma distributions in vivo
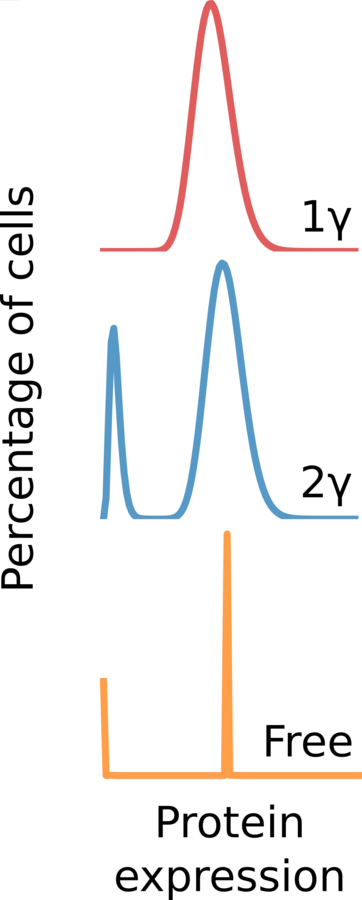
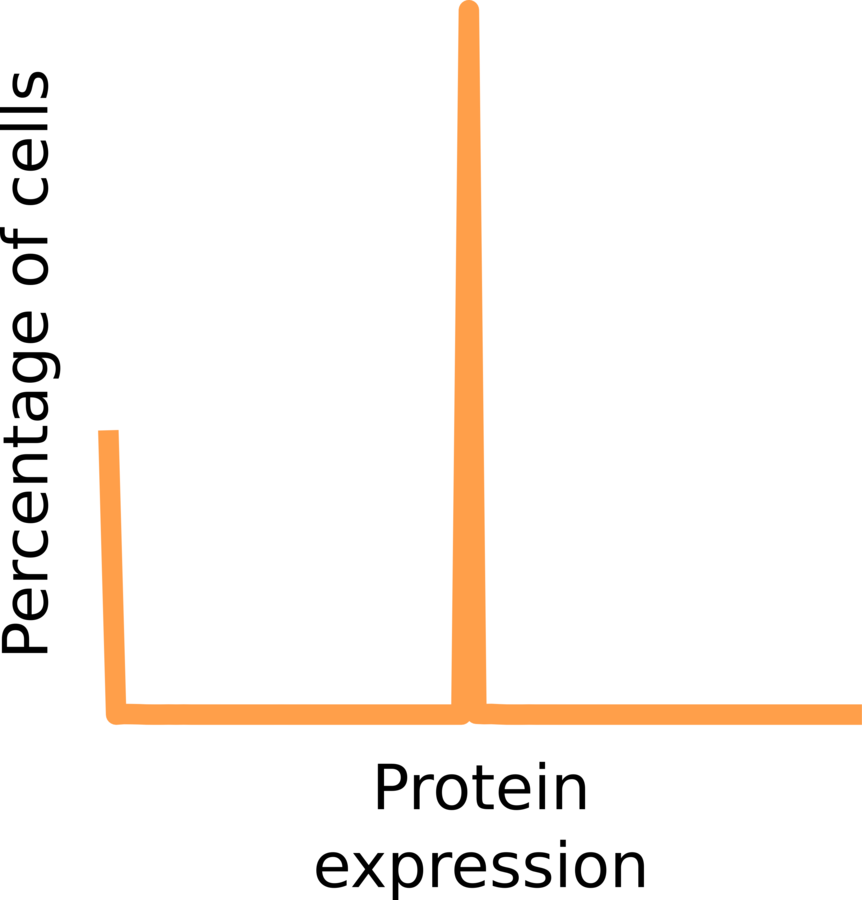
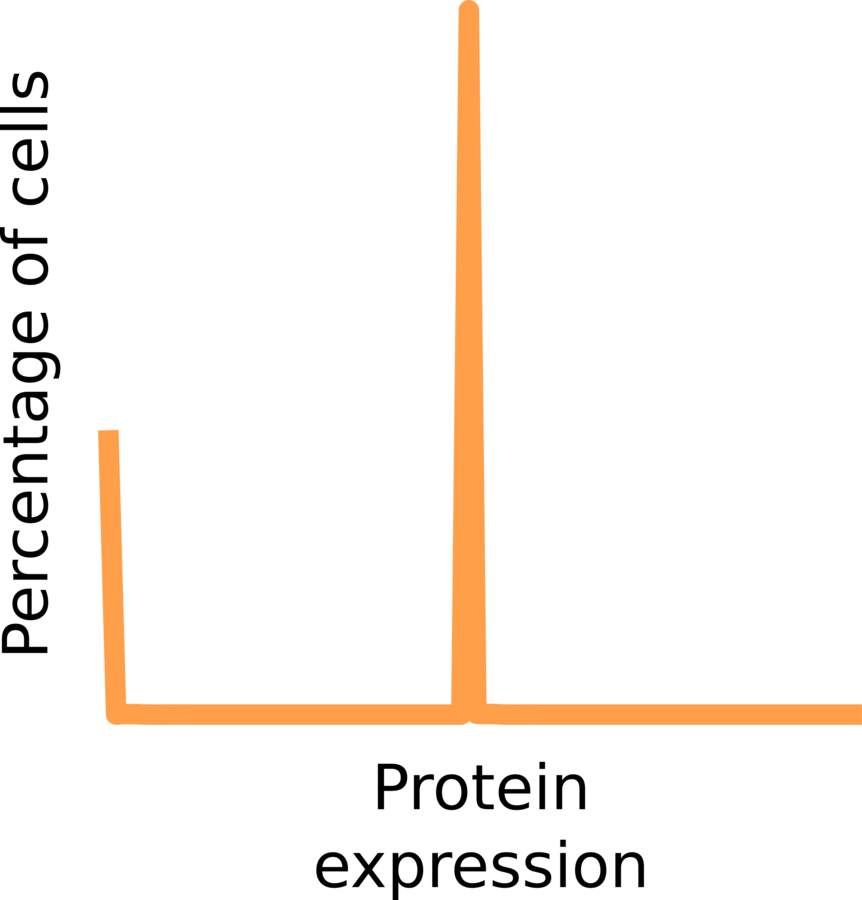
Two-state model of gene expression predicts that the distribution of protein expression follows gamma distributions (Friedman 2006), where:
a = number burst/cell cycle
b = number of proteins/burst
99% of genes follow gamma distributions in vivo (Taniguchi 2010).
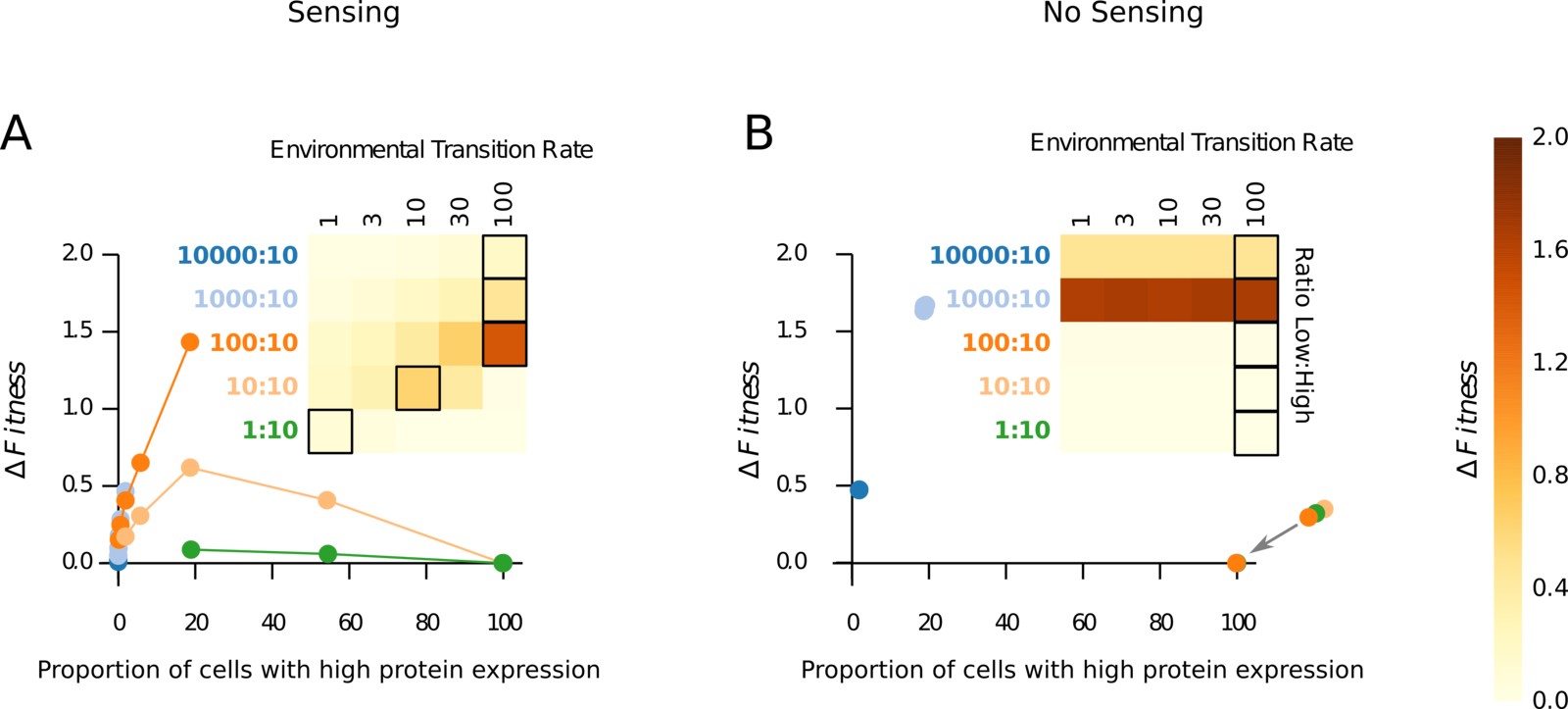
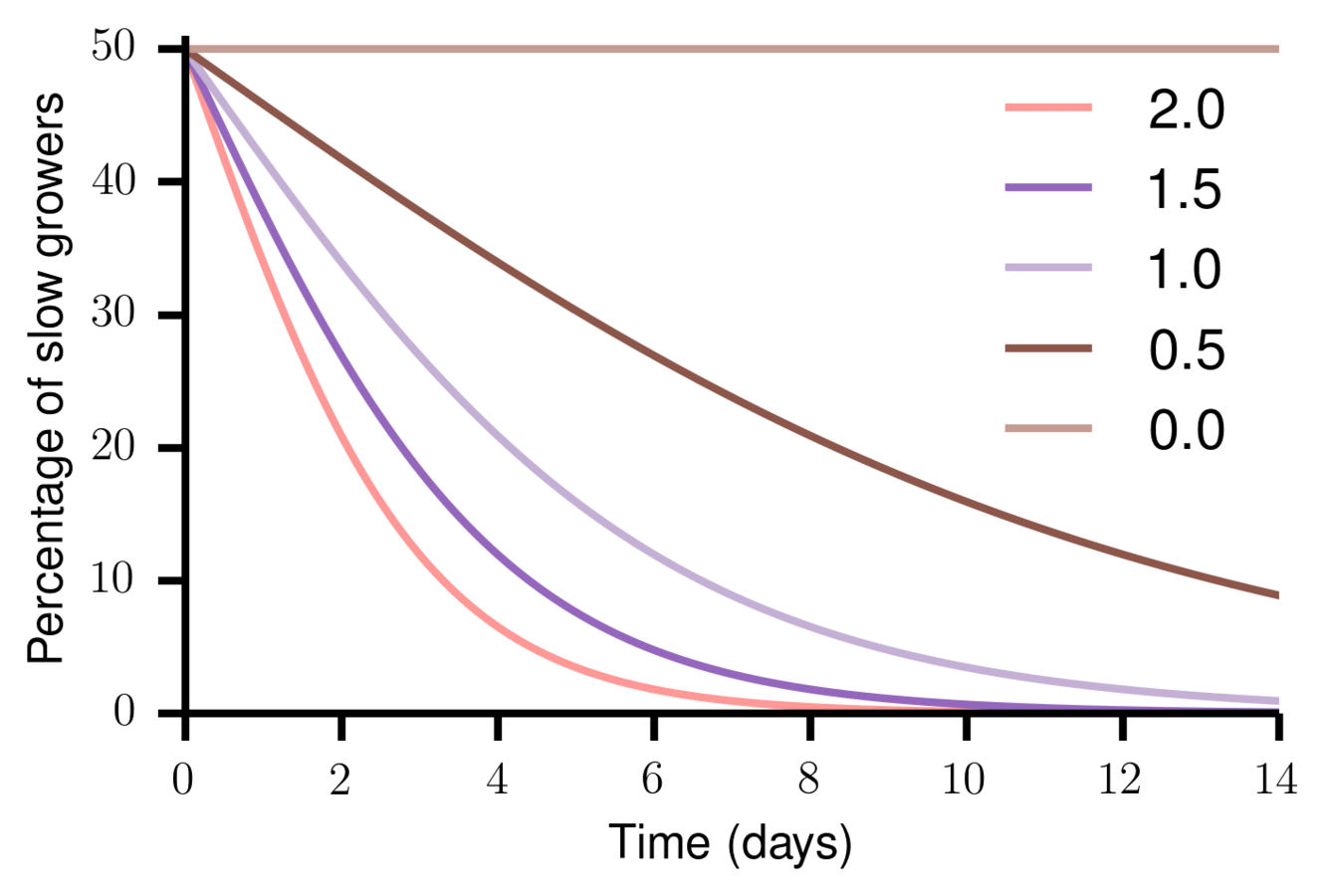
3.4 ΔFitness between 1 and 2
γ
γ
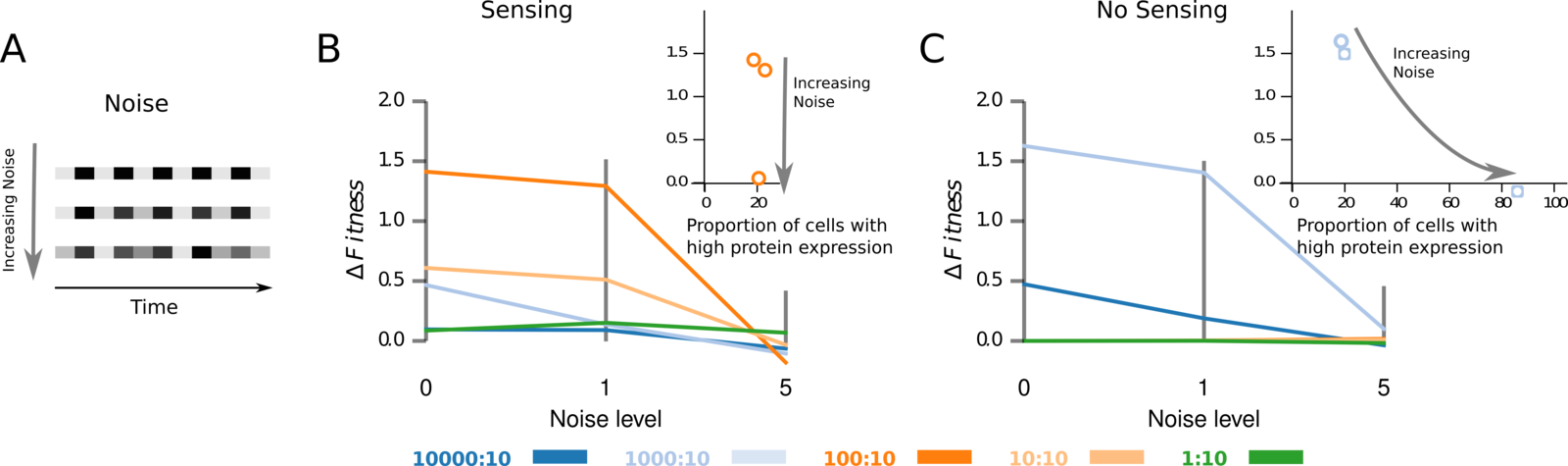
3.5 noise decreases the difference between strategies
3.6 the number of environments
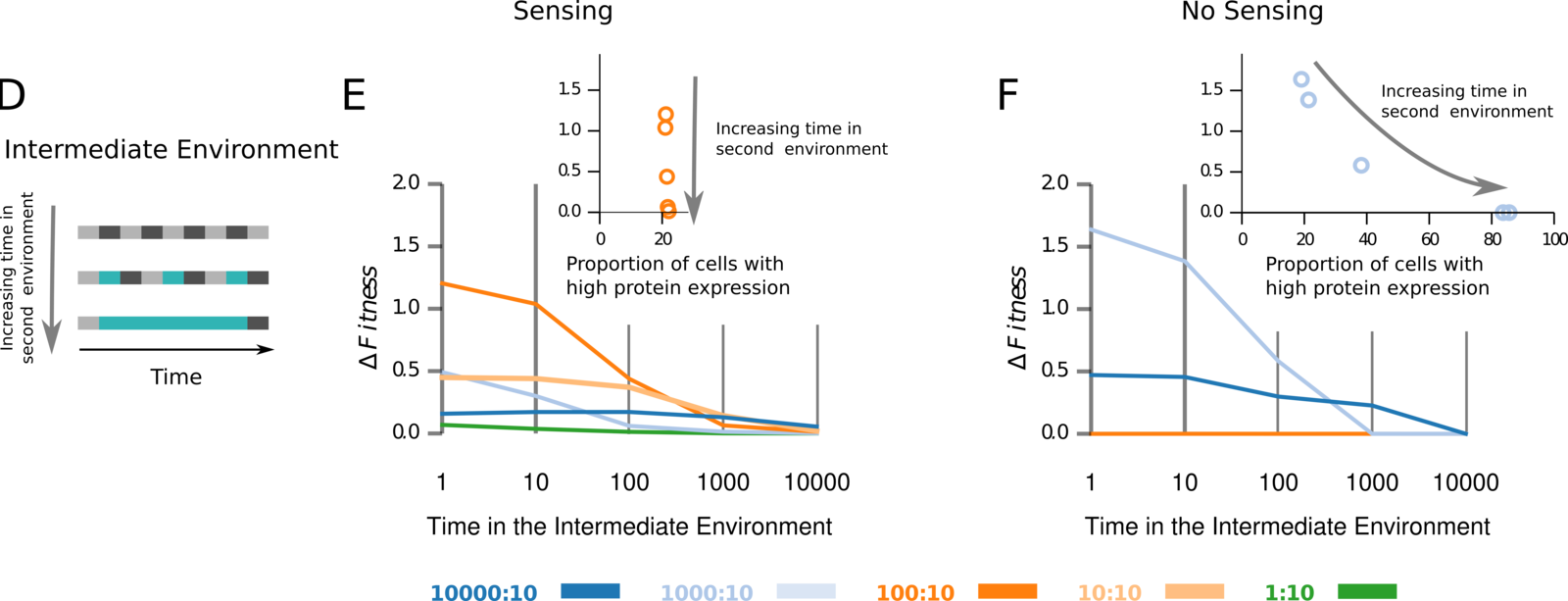
3.6 the number of environments

4. SUMMARY
- Populations of cells can use different strategies to maximize growth in fluctuating environments.
- Bistability is only useful in the presence of strong stressors.
- The optimal strategy is determined by the cost of sensing, the time spent at each environment state, the frequency of environmental transitions and the toxicity of the stressor.
- When the optimal strategy requires many cells induced, bistabilty is preferred.
-
A unimodal phenotype is not worst than a multimodal one. Why do we have multistability?
- Cells needs many genes to eat another sugar, they wouldn't have enough time to prepare all genes if relying in only random fluctuations. It's a strong stressor because they run out of energy before switching to another carbon source if not prepared.
-
Cells need to survive time in the presence of a stressor, they wouldn't be able to do this unless coupled with a sensing mechanism (costly).
-
Stress response with only one gene are unimodal.
- Bonus: Sensing evolves if the cost of sensing is lower than the cost of being maladapted in the second environment.
Bonus
Sensing gives an advantage for symmetric and moderately asymmetric environments, but not for highly asymmetric.
Strong
Weak

Meeting Feb6th
By Javier GB
Meeting Feb6th
Thesis Proposal
- 1,378



