So noisy,
so good.
Javier Garcia-Bernardo
Computer Science Master Student
Math 303. Complex Networks
Background
Genetic networks
Single input motifs

Downstream Gene Expression
Small fluctuations in Activator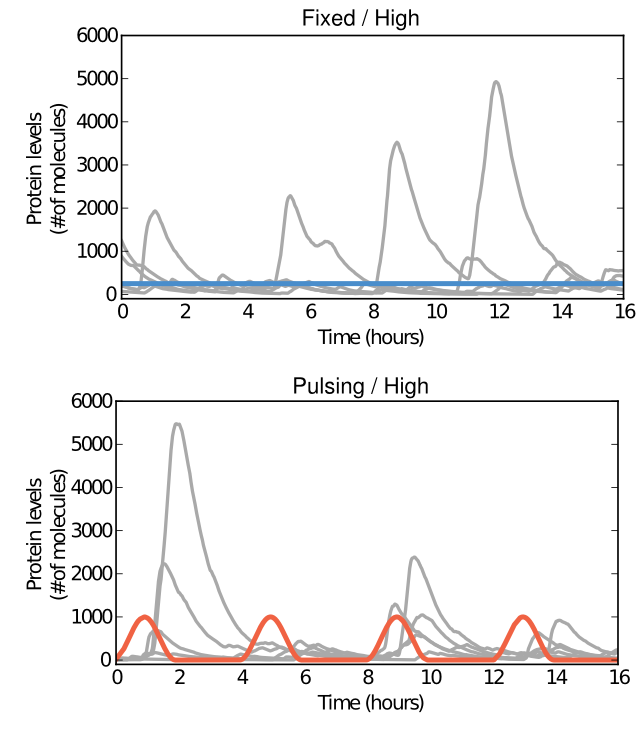
Coordination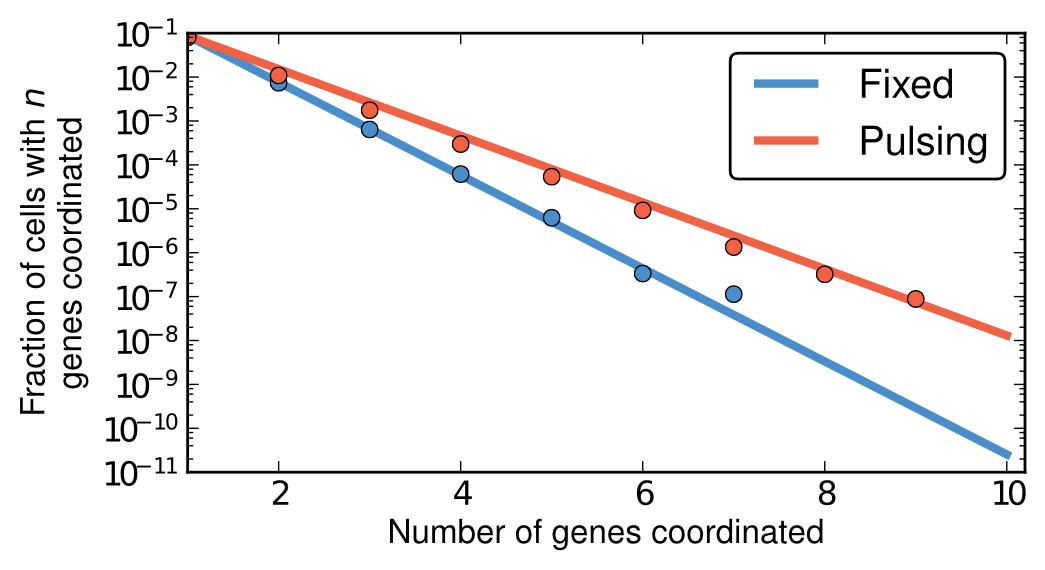

Coordination is good
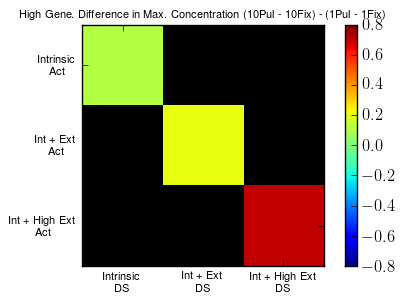
Noise in Gene Expression
Intrinsic: Affect to only one gene.
E.g. RNApolymerase binding to a promoter
Inherent to the Gillespie Algorithm
Extrinsic: Affect to all genes
E.g. Fluctuations in the levels of the RNApolymerase
Modelled with a Ornstein–Uhlenbeck process
Emergence of Coordination
from noise in gene expression


TATA box example
Lots of genes in stress response in yeast have a TATA box.
Is that advantage due to coordination?
Has noise evolved?
Wow
Conclusions
Small fluctuations in the Activator
coordinate expression of Downstream genes.
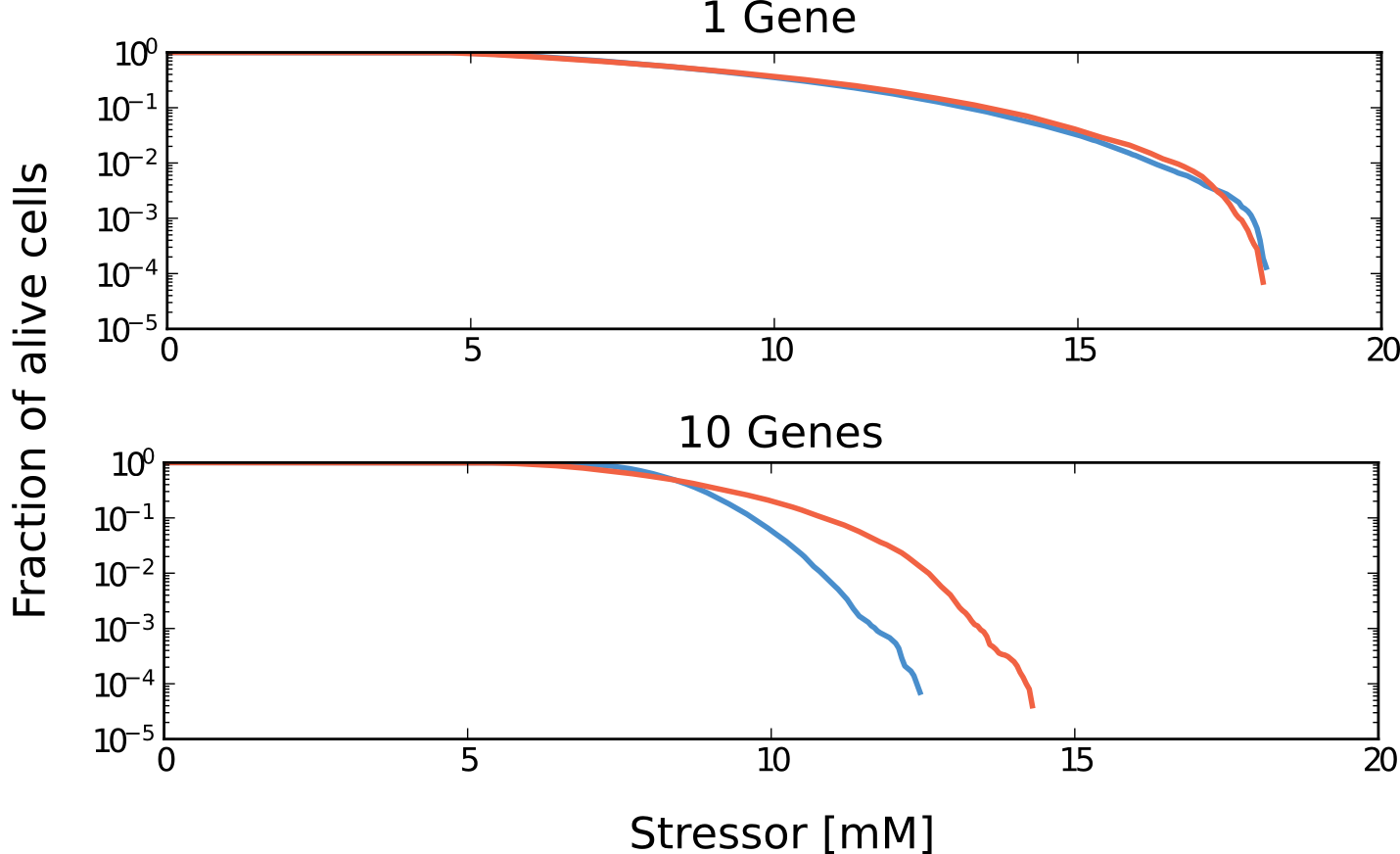
Even Infrequent coordination helps to bet-hedge
against sudden changes in the environment.
They do this without cost (Not shown).
Noise can produce the fluctuations.
Emergence
By Javier GB
Emergence
- 1,287



