Probabilités
Automatismes
Exercices
1) On tire, successivement et avec remise, deux boules dans une urne qui contient deux boules vertes et trois boules jaunes.
Quelle est la probabilité de tirer deux fois une boule verte ?
2) On tire, successivement et sans remise, deux boules dans une urne qui contient deux boules vertes et trois boules jaunes.
Quelle est la probabilité de tirer deux fois une boule verte ?
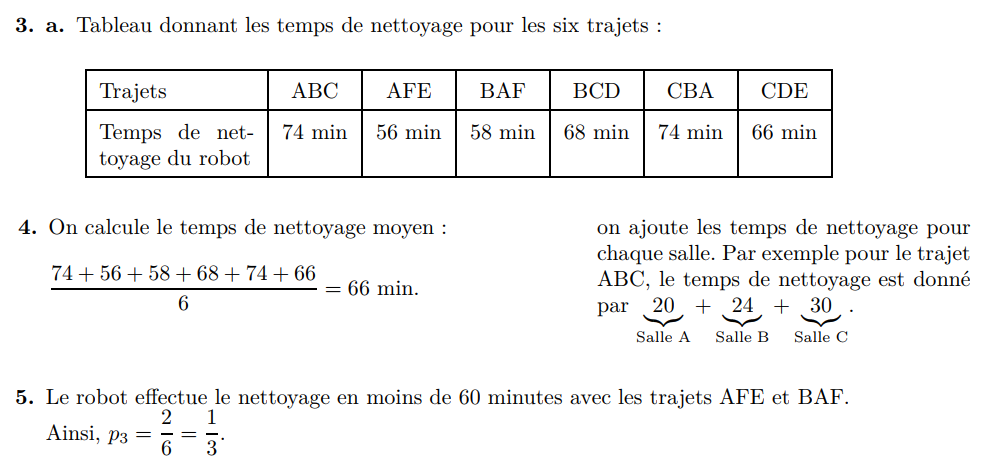
Correction
1) On tire, successivement et avec remise, deux boules dans une urne qui contient deux boules vertes et trois boules jaunes.
Quelle est la probabilité de tirer deux fois une boule verte ?
p=52×52=254
p = \dfrac{2}{5}\times \dfrac{2}{5}= \dfrac{4}{25}
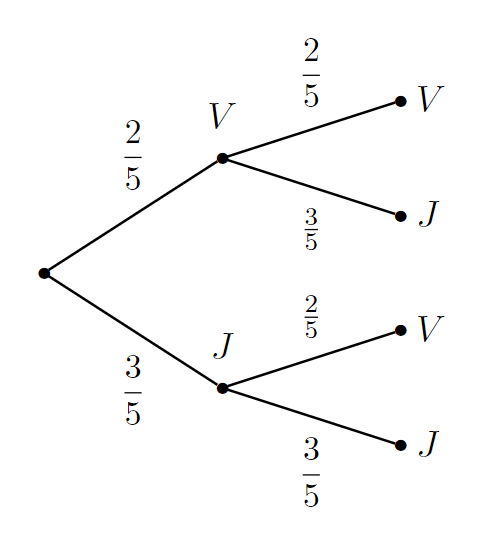
2) On tire, successivement et sans remise, deux boules dans une urne qui contient deux boules vertes et trois boules jaunes.
Quelle est la probabilité de tirer deux fois une boule verte ?
p=52×41=101
p = \dfrac{2}{5}\times \dfrac{1}{4}= \dfrac{1}{10}
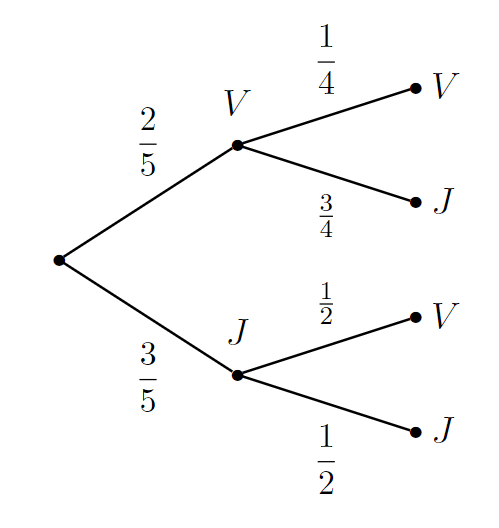
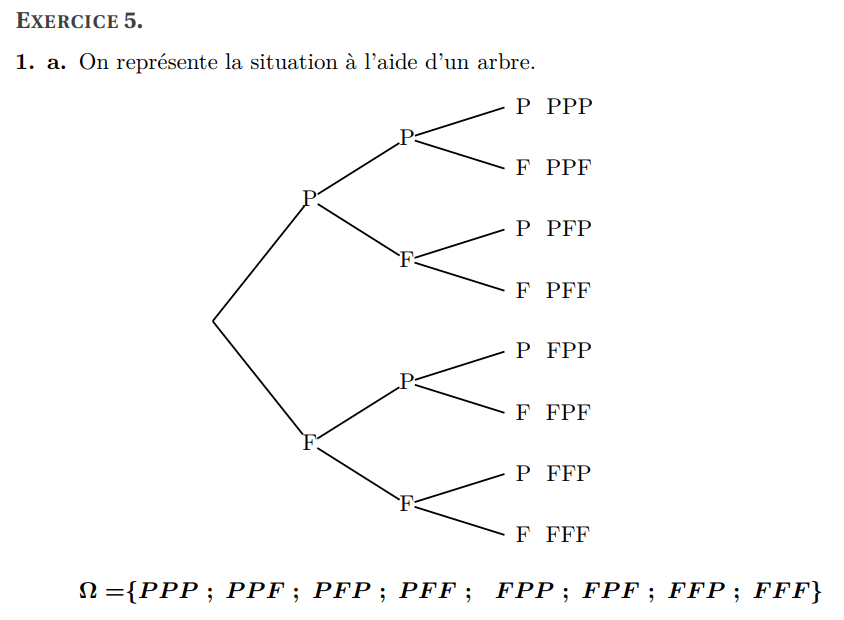
a. 8 tirages possibles.
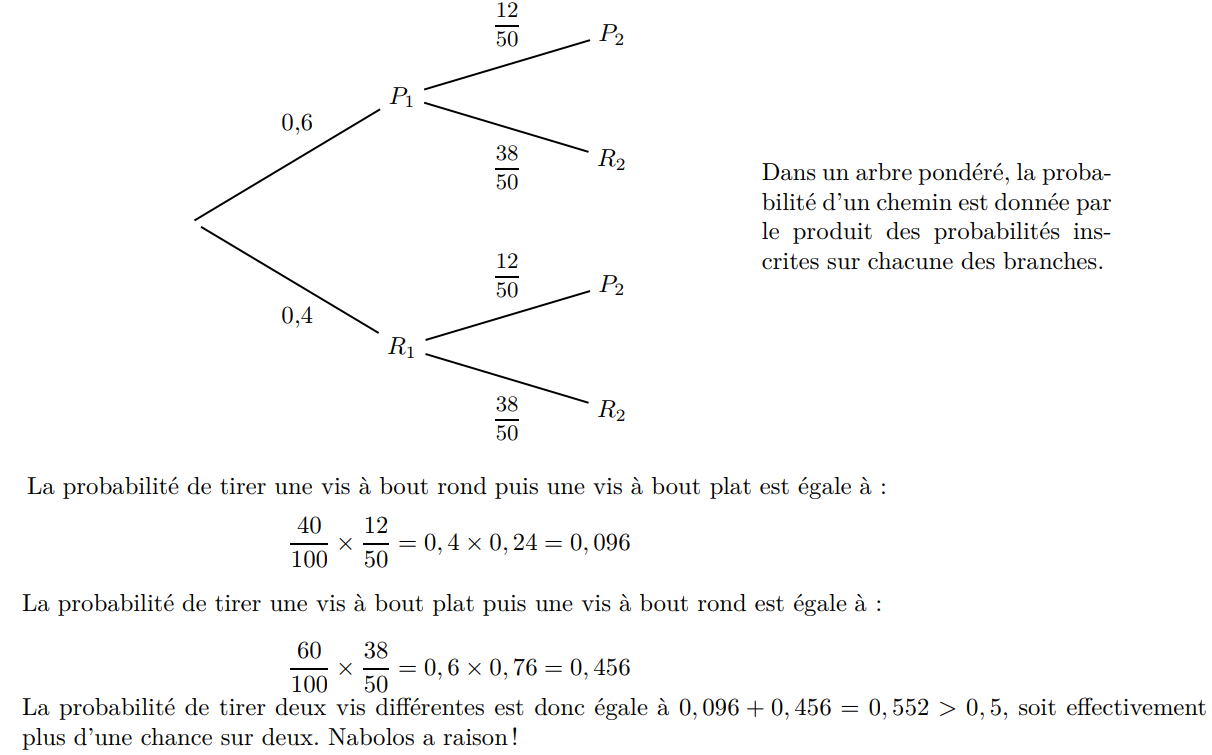
c
c
Version précédente
Probabilités
Activité 1 : Choix de menus
Au restaurant, le menu proposé se compose :
- d’une entrée choisie parmi deux entrée : salade (S) ou charcuterie (C) ;
- d’un plat choisi parmi deux plats : viande (V) ou poisson (P) ;
- d’un dessert choisi parmi deux desserts : fruits (F) ou glace (G).
1. Représenter cette situation à l’aide d’un arbre.
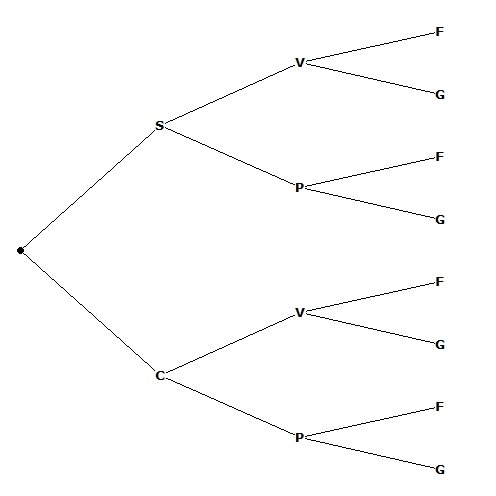
2. Le nombre de branches à « l’arrivée » indique le nombre de tous les choix possibles.
(a) Combien y-a-t-il de menus différents proposés au client ?
(b) Combien y-a-t-il de menus différents si un client veut manger du poisson ?
8 menus différents
4 menus avec du poisson :
(S,P,F) - (S,P,G) - (C,P,F) - (C,P,G)
3. Le restaurateur propose une autre formule : soit une entrée et un plat, soit un plat et un dessert.
Combien y-a-t-il de menus différents possibles dans cette formule ?
Entrée - Plat : 4 menus
(V,F) (V,G) (P,F) (P,G)
Plat - Dessert : 4 menus
(S,V) (S,P) (C,V) (C,P)
Activité 2 : Avec deux dés
On jette deux dés, l’un noir (N), l’autre blanc (B), dont les faces sont numérotés de 1 à 6. On fait la somme des deux nombres obtenus.
On veut déterminer la loi de probabilité des sommes possibles.
1. (a) Reproduire et compléter le tableau à double entrée ci-dessous avec les sommes obtenues.
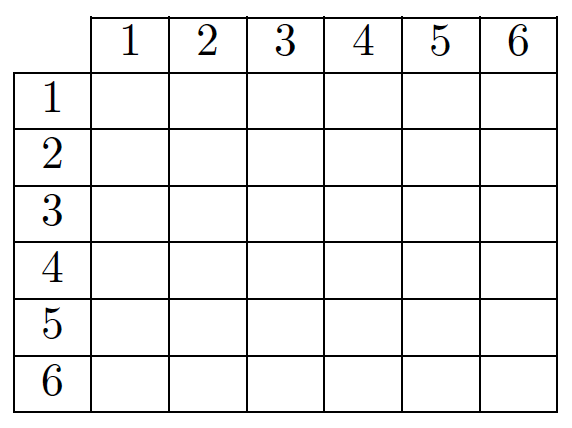
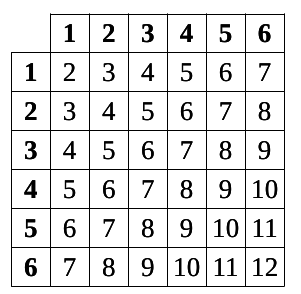
(b) Quel est le tirage le plus fréquent ?
(c) Sachant que les deux dés sont équilibrés, en déduire la loi de probabilité des sommes obtenues.
le 7 (6 fois)
Activité 3 : Tirages de jetons
Une urne contient 12 jetons, numérotés de 1 à 12. Les jetons numérotés de 1 à 5 sont rouges et les autres sont noirs. Les jetons sont indiscernables au toucher. On tire un jeton au hasard.
1. On note A l’événement « Le jeton tiré est rouge ».
(a) Donner la liste des issues de l’événement A.
(b) Déterminer la probabilité de l’événement A (on la notera p (A)).
(a) A = {1 ; 2 ; 3 ; 4 ; 5 }
(b)p(A)=125
(b) \;p(A) = \dfrac{5}{12}
2. On note l’événement contraire de A.
(a) Décrire l’événement par une phrase.
A
\overline{A}
A
\overline{A}
est l'événement "Le jeton tiré est noir".
(b) Donner la liste des issues de l’événement
A={6;7;8;9;10;11;12}
\overline{A}=\{6 ;7;8;9;10;11;12\}
A
\overline{A}
A.
\overline{A}.
(c) Déterminer la probabilité de l’événement
A
\overline{A}
p(A)=127
p(\overline{A})=\dfrac{7}{12}
(d) Quelle relation lie
p(A)etp(A)?
p(A)\;et\;p(\overline{A})?
p(A)=1−p(A)
p(\overline{A})=1-p(A)
3. Reprendre les questions 1 et 2 pour l’événement B : « Le jeton tiré porte un numéro pair ».
1. On note B l’événement « Le jeton tiré est pair ».
(a) Donner la liste des issues de l’événement B.
(b) Déterminer la probabilité de l’événement B
(a) B = {2 ; 4 ; 6 ; 8 ; 10 ; 12 }
(b)p(B)=126=21
(b) \;p(B) =\dfrac{6}{12}= \dfrac{1}{2}
2. (a) Décrire l’événement par une phrase.
B
\overline{B}
est l'événement "Le jeton tiré est impair".
(b) Donner la liste des issues de l’événement
B={1;3;5;7;9;11}
\overline{B}=\{1;3;5;7;9;11\}
B
\overline{B}
B.
\overline{B}.
(c) Déterminer la probabilité de l’événement
B
\overline{B}
p(B)=126=21
p(\overline{B})=\dfrac{6}{12}=\dfrac{1}{2}
(d) Quelle relation lie
p(B)etp(B)?
p(B)\;et\;p(\overline{B})?
p(B)=1−p(B)
p(\overline{B})=1-p(B)
(a) Décrire l’événement par une phrase.
A∩B
A\cap B
est l'événement "Le jeton tiré est rouge et porte un numéro pair".
(b) Donner la liste des issues de l’événement
A∩B={2;4}
A\cap B=\{2;4\}
(c) Déterminer la probabilité de l’événement
p(A∩B)=122=61
p(A\cap B)=\dfrac{2}{12}=\dfrac{1}{6}
4. On considère l’événement « A et B », noté ("A inter B") réalisé lorsque A et B sont réalisés en même temps.
A∩B
A\cap B
A∩B
A\cap B
A∩B.
A\cap B.
A∩B.
A\cap B.
(a) Donner la liste des issues de l’événement
A∪B={1;2;3;4;5;6;8;10;12}
A\cup B=\{1;2;3;4;5;6;8;10;12\}
(b) Déterminer la probabilité de l’événement
p(A∪B)=129=43
p(A\cup B)=\dfrac{9}{12}=\dfrac{3}{4}
A∪B
A\cup B
A∪B.
A\cup B.
A∪B.
A\cup B.
5. Si on tire un jeton rouge, ou un jeton portant un numéro pair, on dit que l’événement « A ou B » est réalisé. On note cet événement ("A union B").
6. Vérifier l’égalité suivante :
p(A∪B)=p(A)+p(B)−p(A∩B)
p(A\cup B)= p(A)+p(B)-p(A\cap B)
p(A)+p(B)−p(A∩B)=125+126−122=129
p(A)+p(B)-p(A\cap B)=\dfrac{5}{12}+\dfrac{6}{12}-\dfrac{2}{12}=\dfrac{9}{12}
2de : Exercices sur les probabilités
Exercice 1 : On lance un dé cubique et un dé tétraédrique (4 faces), tout deux non pipés (c’est-à-dire parfaitement équilibrés).
1. Quelle est la probabilité pour que la somme des faces obtenues soit un multiple de 3 ?
2. Avec les deux chiffres obtenus, on forme un nombre dont le chiffre des unités est celui obtenu avec le dé cubique et celui des dizaines, obtenu avec le dé tétraédrique.
a. Quelle est la probabilité pour que ce nombre soit un multiple de 3 ?
b. Quelle est la probabilité pour que ce nombre soit un multiple de 2 ?
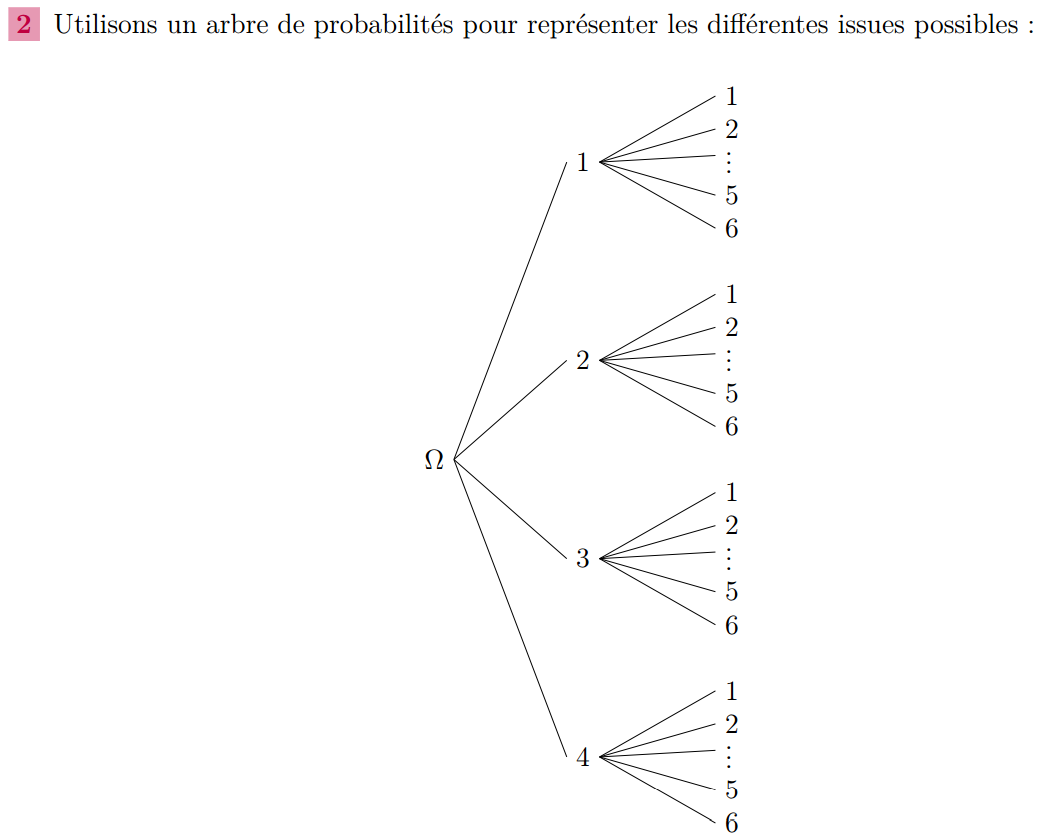
3. Reprendre les questions a et b de la question précédente en considérant maintenant que le chiffre des unités est donné par le dé tétraédrique et celui des dizaines par le dé cubique.
Exercice 2 : Un jeu de cartes est constitué de 52 cartes. On tire au hasard une carte de ce jeu.
1 Quelle est la probabilité d’obtenir une figure rouge ?
2. Quelle est la probabilité d’obtenir une figure ou une carte rouge ?
3. Quelle est la probabilité d’obtenir une figure rouge ou une carte noire qui ne soit pas une figure ?
Exercice 3 :
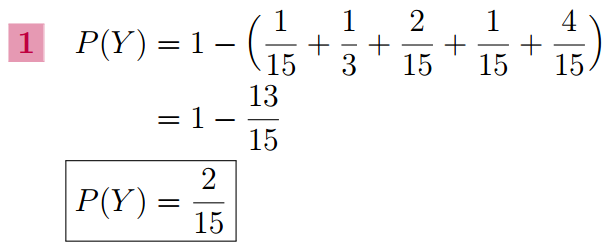
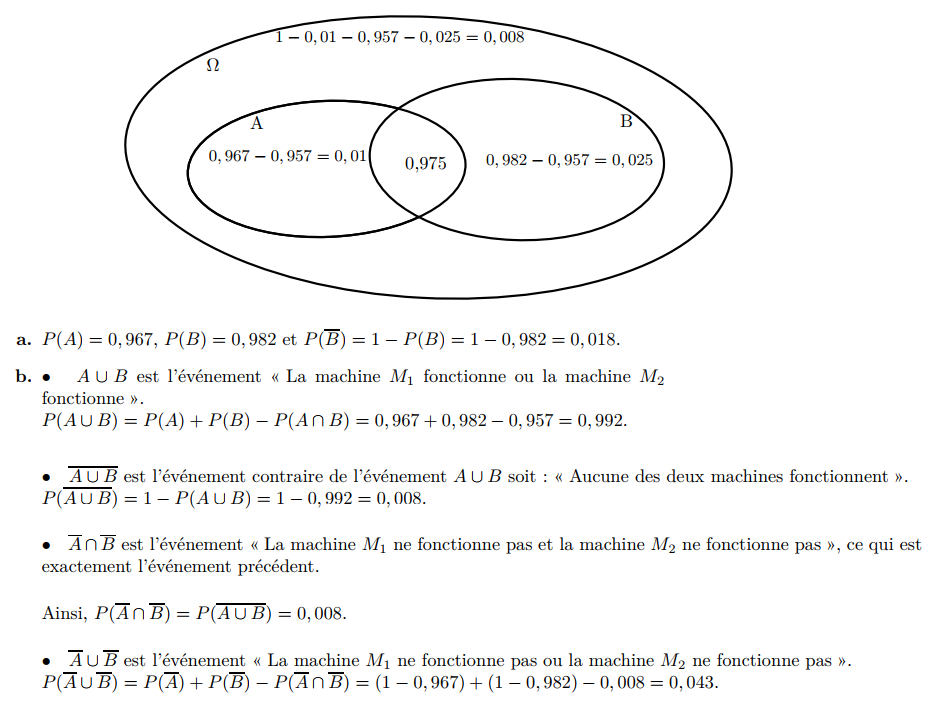
2. Calculer P(M).
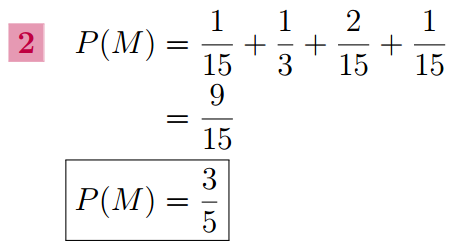
3. Calculer P(Y∩M).
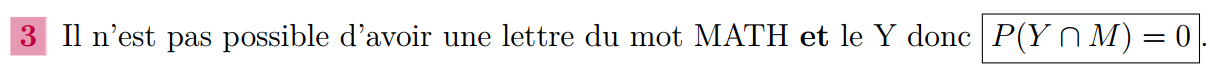
4. Calculer P(Y∪M).
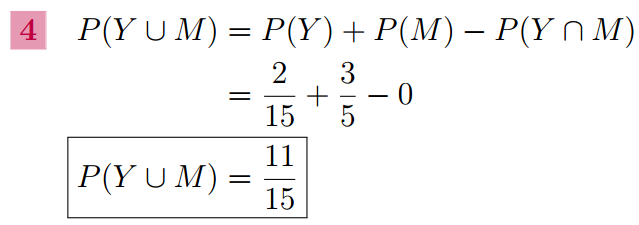
Exercice 4 :
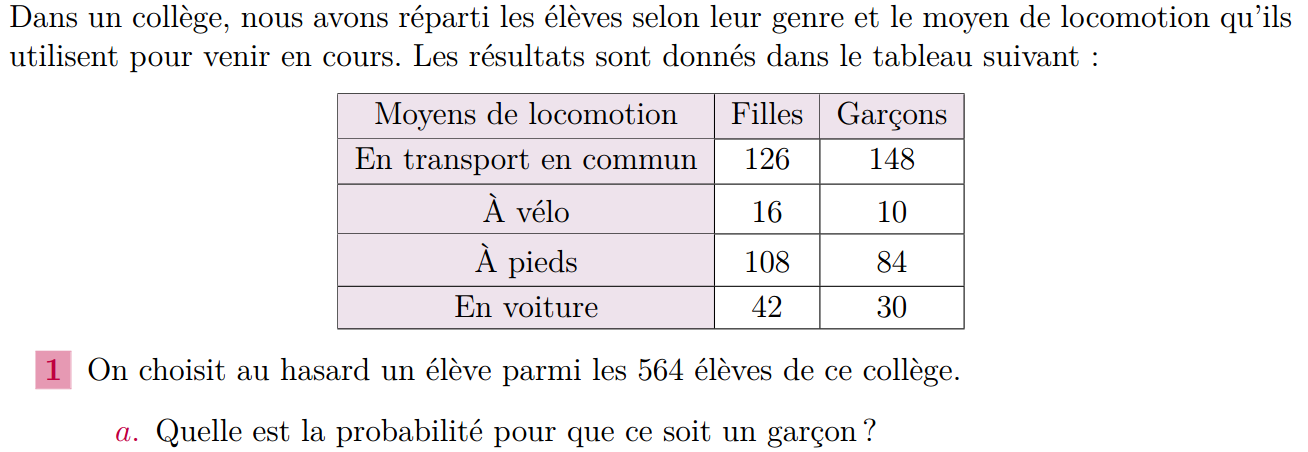
b. Quelle est la probabilité pour que cet élève vienne à vélo ?
c. Quelle est la probabilité pour que ce soit une fille qui vienne à pieds ?
2 On choisit maintenant un garçon au hasard. Quelle est la probabilité pour qu’il vienne en voiture ?
3 On choisit maintenant un élève qui vient en transport en commun. Quelle est la probabilité pour que ce soit une fille ?
Probabilités Automatismes Exercices
2de : Exercices sur les probabilités
By Jean-Marc Kraëber
2de : Exercices sur les probabilités
Lycée Saint-Exupéry - La Rochelle
- 4,493
