Fonctions exponentielles de base \(a\) et fonction log
Act1 p 54 sur TABLEUR : Baisse exponentielle de prix !
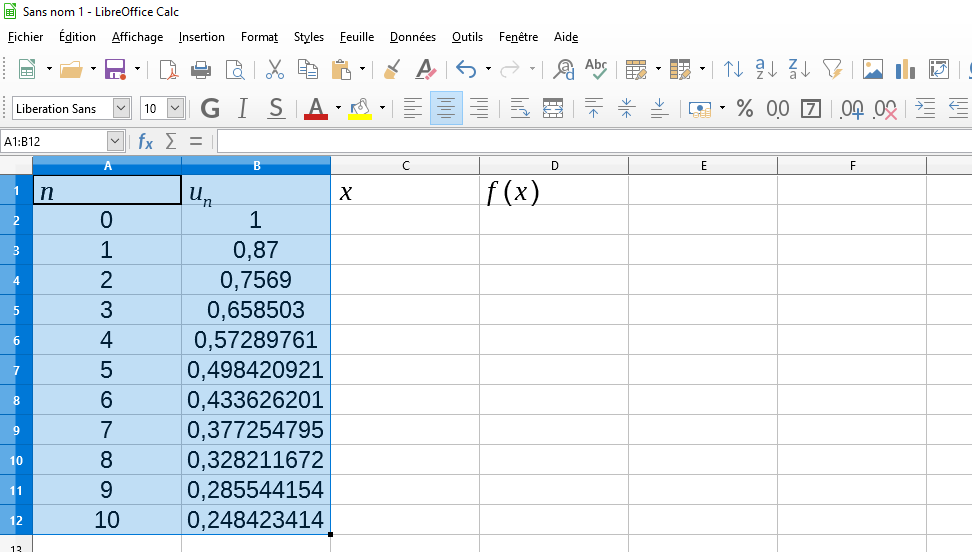
Ouvrir LibreOffice Calc et reproduire la feuille ci-dessous.
- Sélectionner les données.
- Cliquer sur l’icône Diagramme.
Type de diagramme : XY (dispersion) Points seuls
Plage de données : Cocher comme ci-dessous.
Série de données : Ne rien modifier.
Éléments du graphique : Compléter comme ci-dessous.
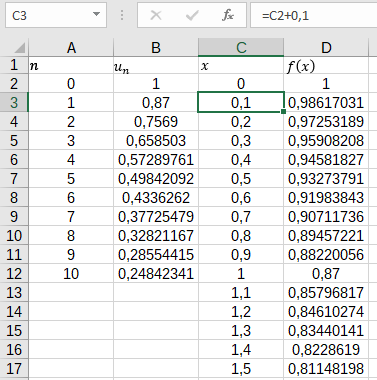
Prendre un pas de 0,1 :
Procéder comme pour la suite \( (u_n) \) :
a)Prix au bout de 5 ans : en B7 on lit 0,4984 donc environ 498,4€
Prix au bout de 2 ans et demi : en D27 on lit 0,7059 donc environ 706€
Prix au bout de 4 ans et 3 mois : en D44, remplacer 4,2 par 4,25 (3 mois représentent 0,25 an) on lit 0,5532 donc environ 553€
b) Au bout de 5 ans environ.
Act1 p 54 sur Calculatrice : Baisse exponentielle de prix !
1. Soit \((u_n)\) une suite géométrique de raison 0,87 et de premier terme \(u_0=1\).
Utiliser la calculatrice pour afficher les 11 premiers termes.
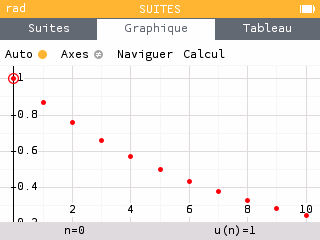
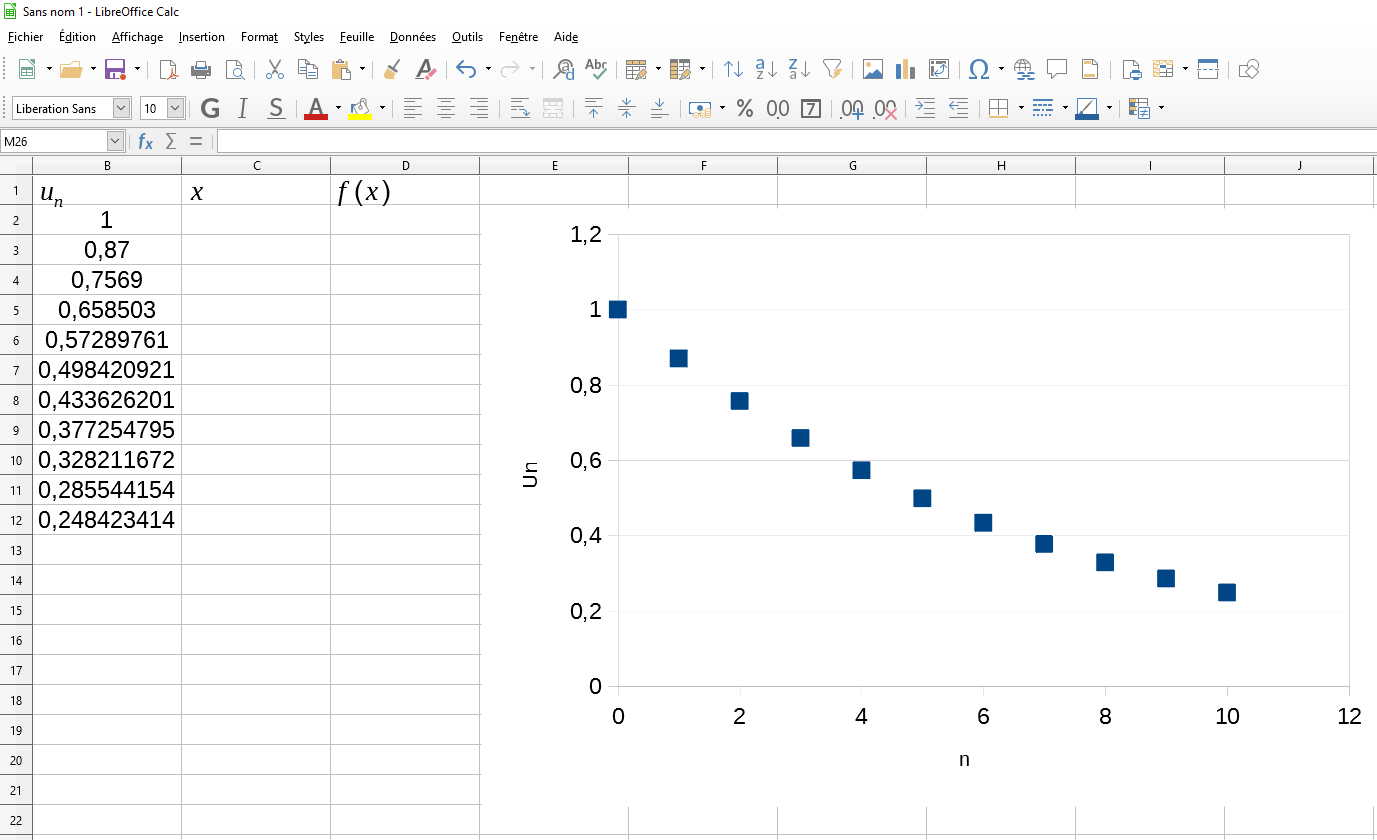
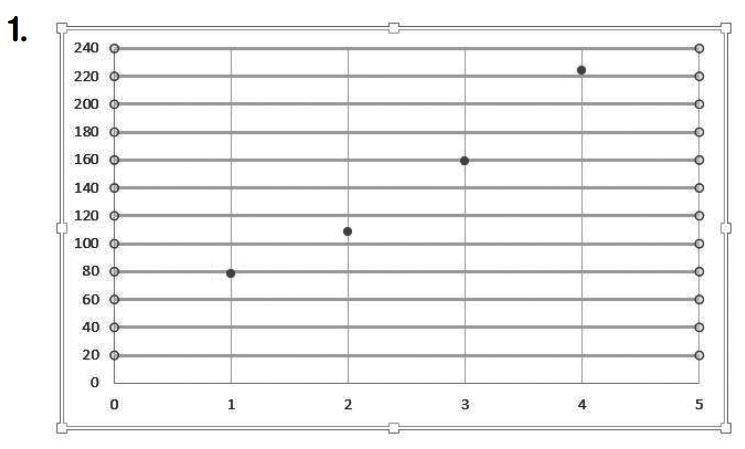
2. Représenter par un nuage de points les 11 premiers termes.
3. Dans le menu grapheur, saisir la fonction définie par
\(f(x)=0,87^x\) pour tout réel \(x\in [0~;~10]\).
Afficher son tableau de valeurs avec un pas de 0,1puis sa représentation graphique.
Réglage de la fenêtre : xmin = 0 et xmax = 10.
Remarque : Les points du nuage appartiennent à la courbe.
4. Le prix d'un smartphone haut de gamme de 1000 € baisse régulièrement de 13% par an. En utilisant la suite \(u\) ou la fonction \(f\), répondre aux questions suivantes.
Prix au bout de 5 ans : avec la suite on lit \(u_5=0,4984\) donc environ 498,4€
Prix au bout de 2 ans et demi : avec la fonction on lit
\(f(2,5) = 0,7059\) donc environ 706€
Prix au bout de 4 ans et 3 mois : avec la fonction, (remplacer 4,2 par 4,25 car 3 mois représentent 0,25 an), on lit \(f(4,25) = 0,5532\) donc environ 553€
Au bout de 5 ans environ.
u_1 = u_0\times q=1\times 2,5 = 2,5
u_{20} = u_0\times q^{20}=1\times 2,5^{20} = 2,5^{20}=90\,949\,470, 18
u_0 = 1000
u_{10} = u_0\times q^{10}=1000\times 1,03^{10} \approx 1344
Au bout de 10 ans sa valeur est d'environ 1344 €.
u_{n+1} = u_n\times\dfrac{3}{2}
On en déduit que \(u_n\) est une suite géométrique de raison \(\dfrac{3}{2}\).
u_{n+1} = 2\left(\dfrac{3}{2}\right)^{n+1}=2\left(\dfrac{3}{2}\right)^{n}\times \dfrac{3}{2}
\(u_0>0\) et \(q>1\) donc la suite \((u_n)\) est croissante.
f(0) = 2^0=1
f(-0,5) = 2^{-0,5}=\dfrac{1}{2^{0,5}}
(2^{0,5})^2 = 2^{0,5\times 2}=2^1=2
\sqrt{2}^2 = 2
On en déduit que \(2^{0,5}=\sqrt{2}\) et plus généralement
a^{0,5}=\sqrt{a}
f(-0,5) = \dfrac{1}{\sqrt{2}}=\dfrac{1\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\dfrac{\sqrt{2}}{2}
f(2,5) = 2^{2,5}=2^{2+0,5}=2^2\times 2^{0,5}=4\sqrt{2}
\text{On cherche une fonction du type }f(x)=k\times \left(\dfrac{1}{3}\right)^x \text{avec }k\in \R
f(0)=-2\text{ équivaut à }k\times \left(\dfrac{1}{3}\right)^0 =-2.
\text{On en déduit que }k =-2.
\text{Conclusion : la fonction cherchée est }f(x)=-2\times \left(\dfrac{1}{3}\right)^x
f(0)=-3(0,25)^{0}=-3
f(-1)=-3(0,25)^{-(-1)}=-3\times 0,25=-0,75
f(0,5)=-3(0,25)^{-0,5}=\dfrac{-3}{0,25^{0,5}}=\dfrac{-3}{\sqrt{0,25}}=\dfrac{-3}{0,5}=-6
9 p 61 : Résoudre une équation avec une fonction exponentielle
Résoudre l'équation : \(0,75^x=5,5\)
Numworks :
Valeur approchée de la solution de l'équation : \(x\approx -5,93\)
Casio : \(0,75^x=5,5\Leftrightarrow 0,75^x-5,5=0\)
SHIFT F3 : V-Window
F6 DRAW :
F1 : ROOT
SHIFT F5 : GSOLVE
TI : \(0,75^x=5,5\Leftrightarrow 0,75^x-5,5=0\)
f(x)
2nde trace : calculs
2 : racine
Borne droite : -5
Borne gauche : -7
Valeur initiale : Ignorer
entrer
On peut procéder comme dans l'exercice 9 p 61 ou utiliser le tableau de valeurs de la fonction \(x\mapsto 3,5^x\)
(méthode par balayage).
La valeur cherchée est comprise entre 5 et 6.
On règle l'intervalle :
La valeur cherchée est comprise entre 5,5 et 5,6.
On règle à nouveau l'intervalle :
La valeur cherchée est comprise entre 5,51 et 5,52.
On règle à nouveau l'intervalle :
Valeur de \(x\) à \(10^{-3}\) près : 5,514
Il s'agit de montrer que l'équation \(f(x)=2\) n'a pas de solution.
-3\times a^x=2 \text{ équivaut à }a^x=-\dfrac{2}{3}.
Or \(a^x>0\) donc cette équation n'admet pas de solution.
On en déduit que 2 n'a pas d'antécédent par \(f\).
\(f\) et \(g\) semblent être des fonctions exponentielles de base \(a>0\) .
Méthode : Retrouver la base d'une fonction exponentielle
f(x) = a^x
f(1) = a^1 = a\text{ et }f(-1) = a^{-1} = \frac{1}{a}
f(1)=0,8\text{ donc }a= 0,8\text{ d'où }f(x)= 0,8^x.
g(-1)=0,6\text{ donc }\dfrac{1}{a}=0,6\text{. On en déduit que }a = \dfrac{1}{0,6} =\dfrac{5}{3}
\text{et }g(x) = \left(\dfrac{5}{3}\right)^x.
g(-3) = 0,216\neq 0,2\text{ donc A n’est pas un point de }C_g.
\text{On doit résoudre l'équation }0,8^x=3.
x\approx -4,92
On modélise l'évolution du compte de Mélissa avec la fonction :
f(x)=992\times 1,0075^x
On convertit deux ans, trois mois, quatre jours en années :
2+\dfrac{3\times31}{365}+\dfrac{4}{365}\approx 2,266
On convertit 10 ans, 3 mois, 20 jours en années :
10+\dfrac{3\times31}{365}+\dfrac{20}{365}\approx 10,310
f(2,266)\approx1008,94
\text { soit un solde d'environ 1008,94 €.}
On calcule l'image du nombre précédent par la fonction :
f(-10,31)\approx918,45
\text { soit un solde initial d'environ 918,45 €.}
Il faut attendre 93,84 ans soit environ 34 252 jours.
=2^{1,5-(-3,7)+2,3}=2^{7,5}
=3^{1,2-0,8-1,5}=3^{-1,1}
=\pi^{-2,5+2+1,5+0,5}=\pi^{1,5}
=\dfrac{4,1^{-2,7}}{4,1^{-2,1}}=4,1^{-0,6}
=\left(2,25^{3}\times 2,25^{-1,5}\right)^{-1}
=\left( 2,25^{1,5}\right)^{-1}
=2,25^{-1,5}
A=5^{-8}
B=2,7^{-7}
C=4,5^{-0,1}
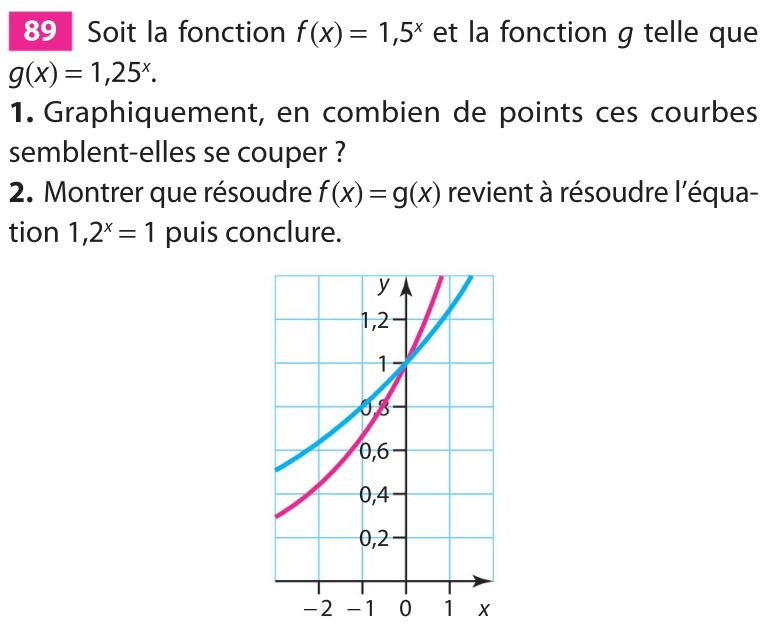
1. En un point.
\text{2. Il faut résoudre l'équation }1,5^x=1,25^{x}
\text{soit }\dfrac{1,5^x}{1,25^{x}}=1.
\dfrac{1,5^x}{1,25^{x}}=1
\left(\dfrac{1,5}{1,25}\right)^x=1
1,2^x=1
x=0
Conclusion : Les deux courbes n'ont qu'un point d'intersection, le point d'abscisse 0.
\(\pi >1\) donc \(f\) est croissante.
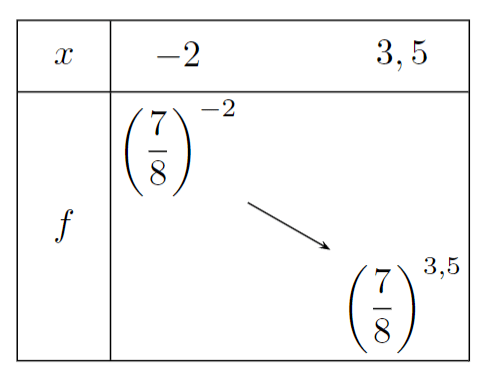
\(\dfrac{7}{8}<1\) donc \(f\) est décroissante.
a.\; g(x)=\dfrac{1}{0,99^x}=\dfrac{1^x}{0,99^x}=\left(\dfrac{1}{0,99}\right)^x
\dfrac{1}{0,99}>1\text{ donc }g\text{ est strictement croissante sur }\mathbb{R}.
b.\; g(x)=\left(\dfrac{1}{1,001}\right)^x
\dfrac{1}{1,001}<1\text{ donc }g\text{ est strictement décroissante sur }\mathbb{R}.
\dfrac{a^x}{b^x}=\left(\dfrac{a}{b}\right)^x
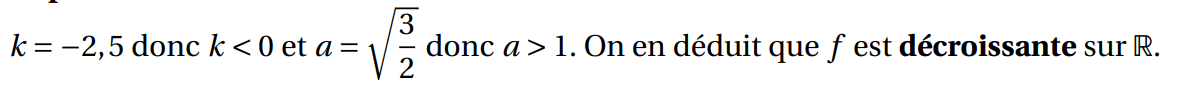
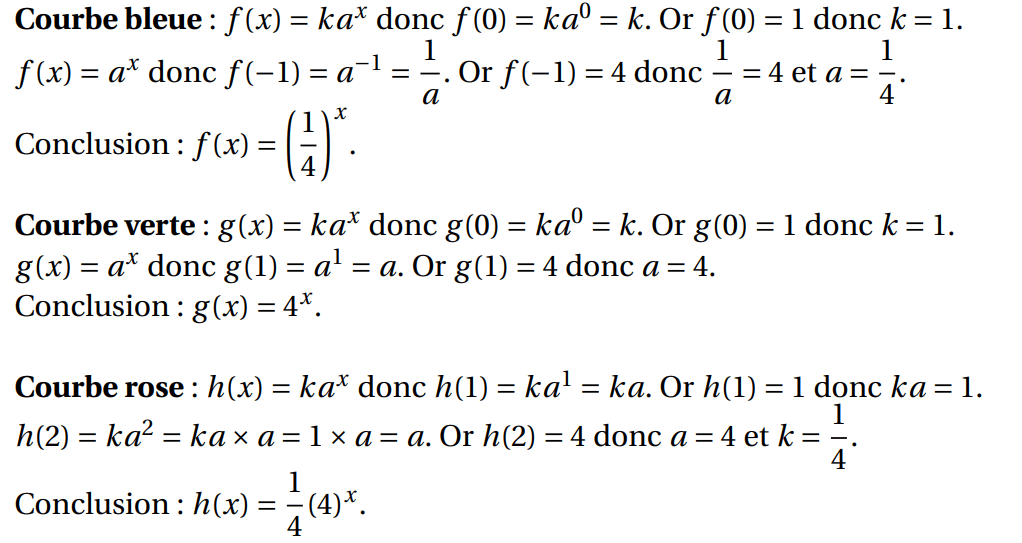
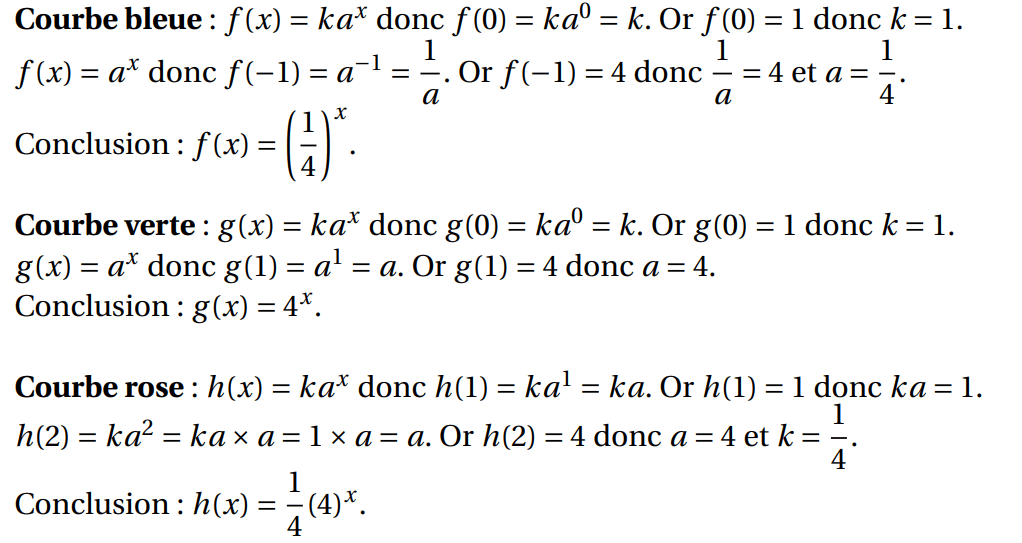
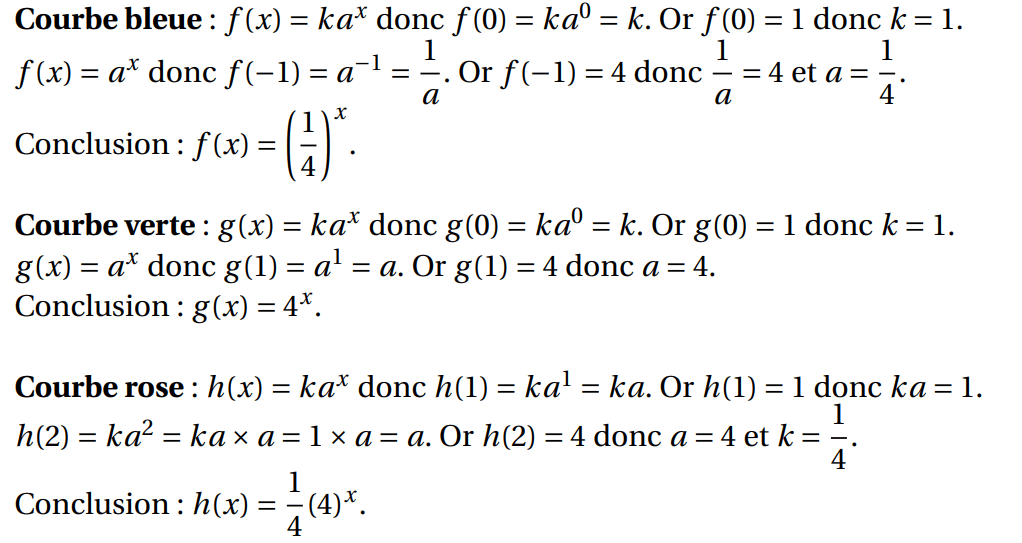
Bleue - Verte - Rose
\text{et }k>0
\text{et }k>0
k<0\text{ et }a>1
f(-1)=2\times 0,5^{-1}=4\text{ donc }A\in C_f.
f(0)=k\times a^{0}=k\times 1=k\text{ donc }k=-2.
f(x)=-2\times a^{x}
f(1)=-2\times a^{1}=-2a\text{ donc }-2a=-1\text{ et }a=0,5\;; f(x)=-2\times 0,5^x
1.\;f(0)=1,5\text{ donc }k=1,5.
f(x)=1,5\times a^{x}
f(-1)=1,5\times a^{-1}=\dfrac{1,5}{a}\text{ donc }\dfrac{1,5}{a}=5\text{ et }a=0,3
f(x)=1,5\times 0,3^{x}
2.\;f(1)=1,5\times 0,3^{1}=0,45
f(3,5)=1,5\times 0,3^{3,5}\approx 0,022
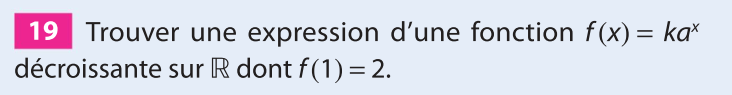
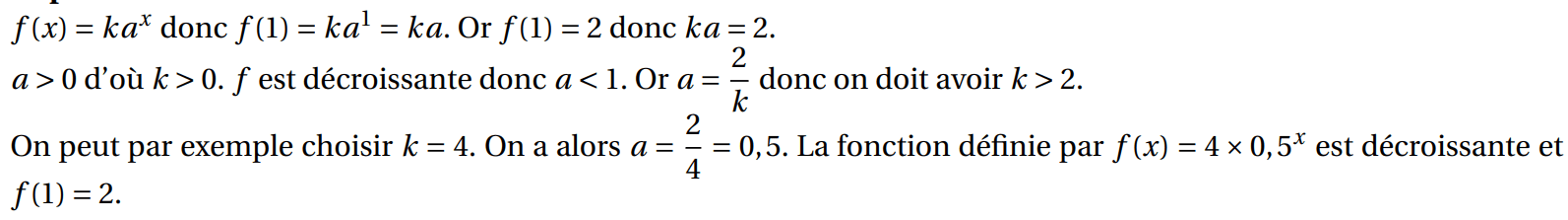
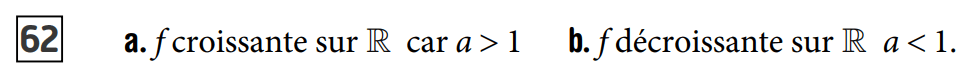
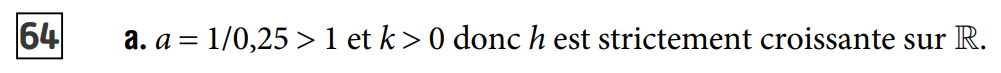
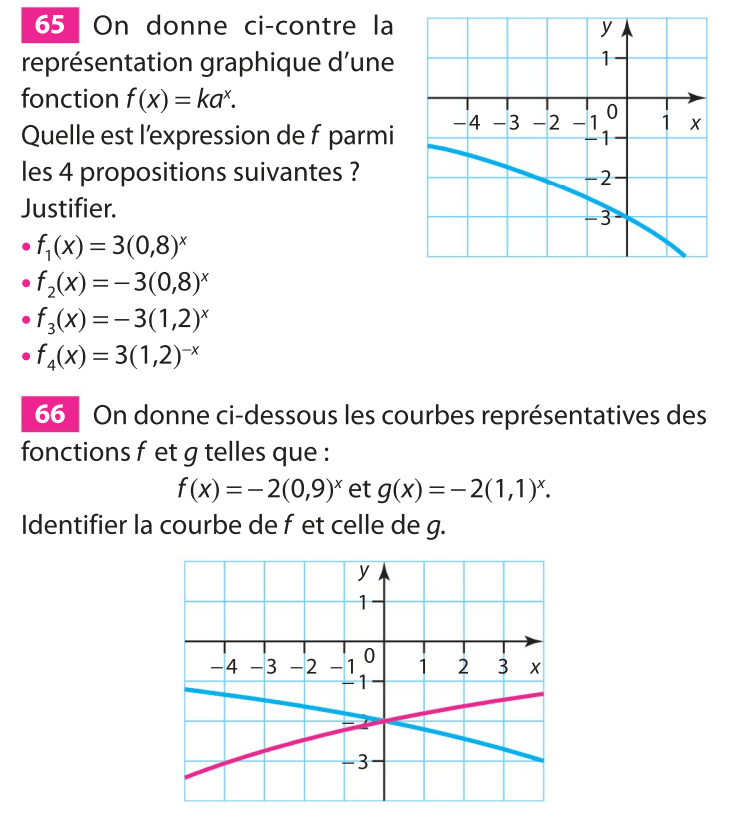
Rq : Inutile de dresser les tableaux de signes, les deux fonctions sont positives.
Pour f : a = 1,05 > 1 donc f est croissante.
Pour g : a =\( \dfrac{1}{1,05} < 1\) donc g est décroissante.
Le prix d’équilibre est solution de l’équation
f(x)=g(x)
1,05^x=7\times 1,05^{-x}
1,05^x=7\times \dfrac{1}{1,05^{x}}
\left(1,05^x\right)^2=7
\left(1,05^2\right)^x=7
1,1025^x=7
À l'aide de la calculatrice on obtient x = 19,94 euros
Log
\text{Exemple 1 : Encadrer }\log(135)\text{ à l'aide de deux entiers relatifs}
100<135<1000 \quad \text{ donc }\quad \log(100)<\log(135)<\log(1000)
2<\log(135)<3
\text{Exemple 2 : Encadrer }\log(0,006)\text{ à l'aide de deux entiers relatifs}
0,001<0,006<0,01 \quad \text{ donc }\quad \log(0,001)<\log(0,006)<\log(0,01)
-3<\log(0,006)<-2
1.~\log(10^x\times 10^y)=\log(10^{x+y})=x+y=\log(10^x)+\log(10^y)
\log(a\times b)=\log(a)+\log(b)
2.~\log(a^2)=\log(a\times a)=\log(a)+\log(a) =2\log(a)
\log(a^n)=n\log(a)
3.~\log\left(b\times \frac{1}{b}\right)=\log\left(b\right)+\log\left( \frac{1}{b}\right)
\log\left(\dfrac{1}{b}\right)=-\log(b)
\text{Or }\log\left(b\times \frac{1}{b}\right)=\log\left(1\right)=0.
\text{On en déduit que }\log\left(b\right)+\log\left( \frac{1}{b}\right)=0.\text{ D'où le résultat suivant :}
1.~~N'=10\log\left(\dfrac{2I}{10^{-12}}\right)=10\log\left(2\times\dfrac{I}{10^{-12}}\right)
=10\left(\log(2)+\log\left(\dfrac{I}{10^{-12}}\right)\right)
=10\log(2)+10\log\left(\dfrac{I}{10^{-12}}\right)
\approx 3+N
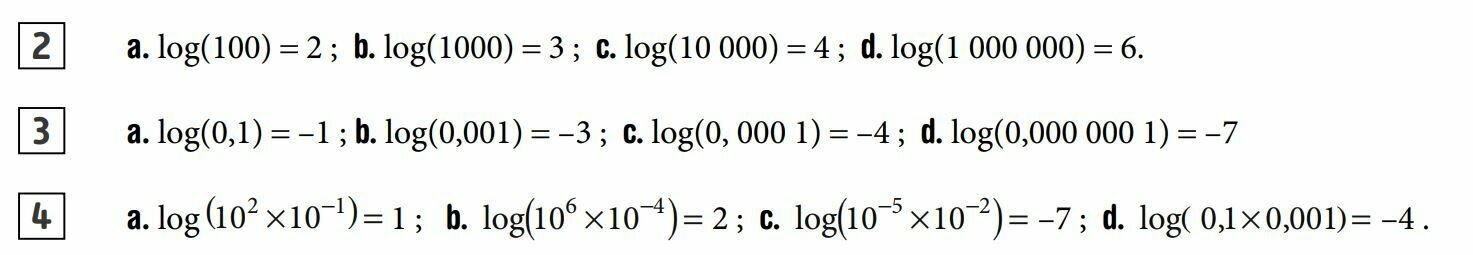
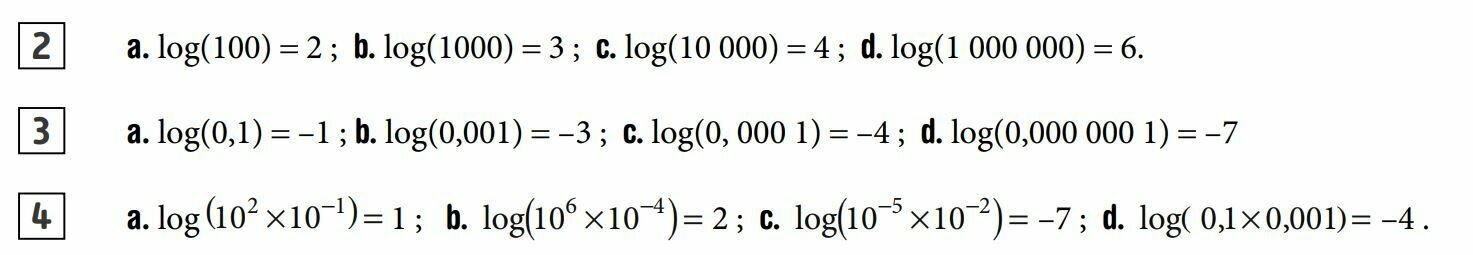
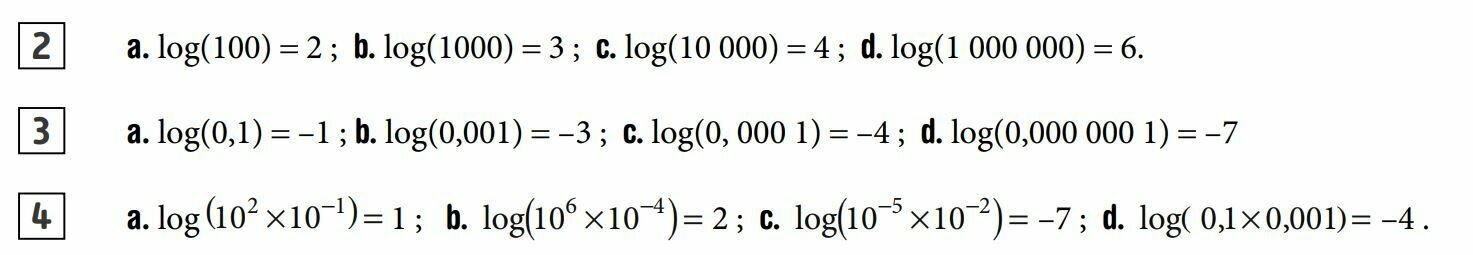
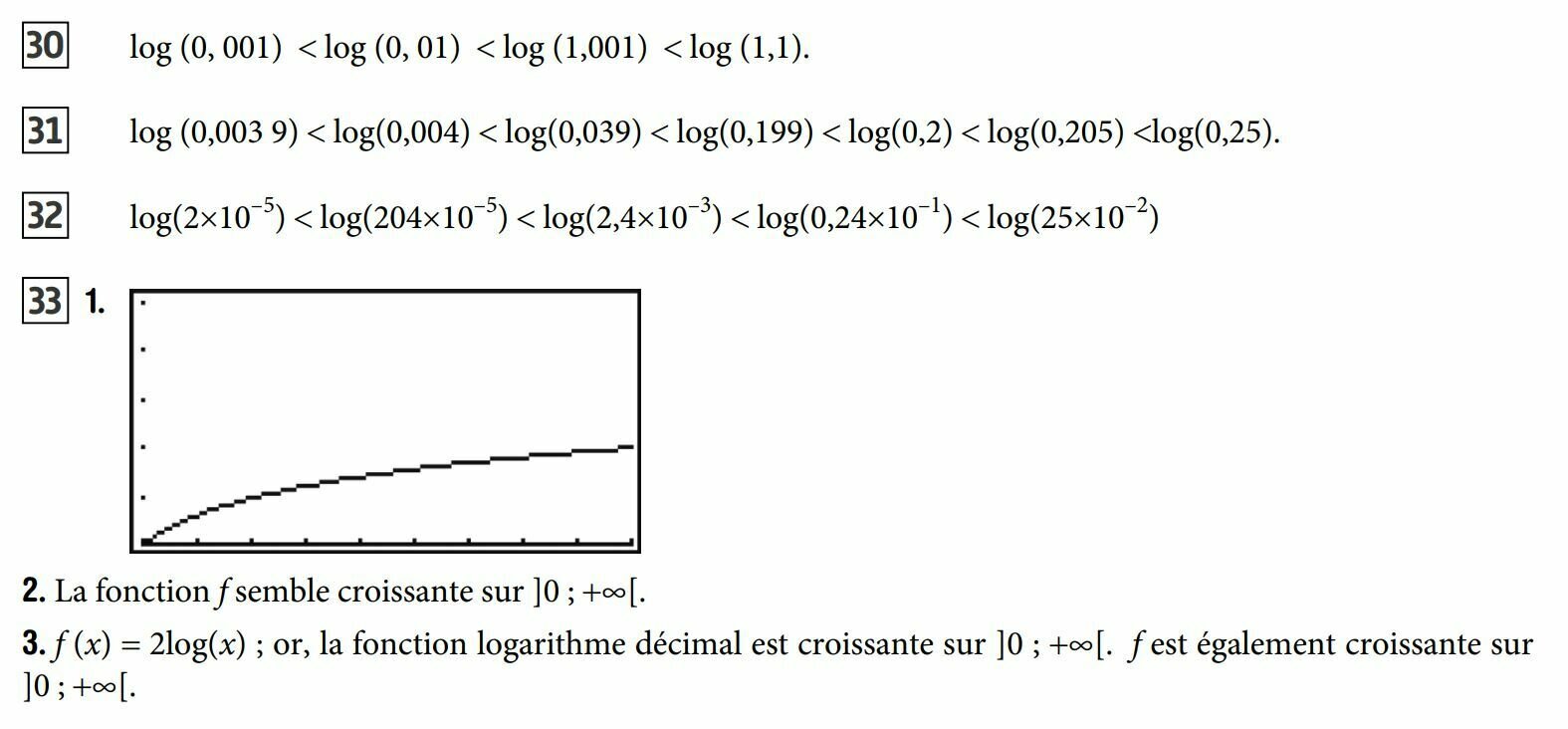
2. Lire "le niveau sonore d'une moto en course est de 90 dB."
D'après la question 1. le niveau sonore des deux motos côte à côte est d'environ 93 dB."
\text{a. }\log\left(200\right)=\log\left(100\times 2\right)=\log(100)+\log(2) = 2 +\log(2).
\text{b. }\log\left(400\right)= 2 +\log(4)=2+\log\left(2^2\right)=2+2\log(2).
\text{c. }\log\left(80\right)= 1 +\log(8)=1+\log\left(2^3\right)=1+3\log(2).
\text{d. }\log\left(32\right)=\log\left(2^5\right)=5\log(2).
\text{a. }\log\left(0,2\right)=\log\left(\dfrac{2}{10}\right)=\log(2)-\log(10) =\log(2)-1.
\text{b. }\log\left(0,004\right)=\log\left(\dfrac{4}{1000}\right)=\log(4)-\log(1000) =2\log(2)-3.
\text{c. }\log\left(0,08\right)=\log\left(\dfrac{8}{100}\right)=\log(8)-\log(100) =3\log(2)-2.
\text{d. }\log\left(0,032\right)=\log\left(\dfrac{32}{1000}\right)=\log(32)-\log(1000) =5\log(2)-3.
\text{a. }\log\left(25\right)=\log\left(5^2\right)=2\log(5).
\text{b. }\log\left(125\right)=3\log(5)
\text{c. }\log\left(50\right)=\log\left(10\times 5\right)=\log(10)+\log(5) = 1 +\log(5).
\text{d. }\log\left(25000\right)=\log\left(1000\times 25\right)=\log(1000)+\log(25) = 3 +2\log(5).
\text{a. }\log\left(0,5\right)=\log\left(\dfrac{5}{10}\right)=\log(5)-\log(10) =\log(5)-1.
\text{b. }\log\left(0,0025\right)=\log\left(\dfrac{25}{10000}\right)=\log(25)-\log(10000) =2\log(5)-4.
\text{c. }\log\left(0,625\right)=\log\left(\dfrac{625}{1000}\right)=\log(625)-\log(1000) =4\log(5)-3.
\text{d. }\log\left(0,005\right)=\log\left(\dfrac{5}{1000}\right)=\log(5)-\log(1000) =\log(5)-3.
\text{a. }\log\left(6\right)=\log\left(2\times 3\right)=\log(2)+\log(3).
\text{b. }\log\left(24\right)= \log(8\times 3)=\log\left(8\right)+\log(3)=3\log\left(2\right)+\log(3).
\text{c. }\log\left(18\right)=\log(2\times 9)=\log\left(2\right)+\log(9)=\log\left(2\right)+2\log(3).
\text{d. }\log\left(1200\right)=\log\left(12\times 100\right)=\log(4\times 3)+\log(100)=2+2\log(2)+\log(3).
\text{a. }\log\left(500\right)=\log\left(100\times 5\right)=\log(100)+\log(5)=2+\log(5).
\text{c. }\log\left(50000\right)=\log(10000\times 5)=\log\left(10000\right)+\log(5)=4+\log(5).
\text{b. }\log\left(0,05\right)=\log\left(\dfrac{5}{100}\right)=\log(5)-\log(100) =\log(5)-2.
\text{d. }\log\left(0,25\right)=\log\left(\dfrac{25}{100}\right)=\log(25)-\log(100) =2\log(5)-2.
\text{a. }\log\left(9\right)=\log\left(3^2\right)=2\log(3).
\text{b. }\log\left(27\right) =3\log(3).
\text{d. }\log\left(30\right)=\log\left(3\times 10\right)=\log(3)+\log(10) =\log(3)+1.
\text{c. }\log\left(0,3\right)=\log\left(\dfrac{3}{10}\right)=\log(3)-\log(10) =\log(3)-1.
\text{a. }\log\left(25\right)+\log\left(2\right)=\log(25\times 2)=\log(50).
\text{d. }\log\left(100\right)+\log\left(0,25\right)=\log(100\times 0,25 )=\log(25).
\text{b. }\log\left(27\right)-\log\left(3\right)=\log\left(\dfrac{27}{3}\right)=\log(9).
\text{c. }\log\left(4\right)-\log\left(8\right)=\log\left(\dfrac{4}{8}\right)=\log(0,5).
\text{a. }\log\left(0,1\right)+\log\left(200\right)=\log(0,1\times 200)=\log(20).
\text{c. }\log\left(0,002\right)+\log\left(10000\right)=\log(0,002\times 10000 )=\log(20).
\text{b. }\log\left(500\right)-\log\left(125\right)=\log\left(\dfrac{500}{125}\right)=\log(4).
\text{c. }\log\left(25\right)=2\log(5)\approx 1,4.
\text{a. }\log\left(0,5\right)=\log\left(\dfrac{5}{10}\right)=\log(5)-\log(10) =\log(5)-1\approx0,7-1=-0,3.
\text{b. }\log\left(0,05\right)=\log\left(\dfrac{5}{100}\right)=\log(5)-\log(100) =\log(5)-2\approx -1,3.
\text{d. }\log\left(500\right)=\log\left(5\times 100\right)=\log(5)+\log(100) =\log(5)+2\approx 2,7.
\text{c. }\log\left(8\right)=3\log(2)\approx 0,9.
\text{a. }\log\left(0,2\right)=\log\left(\dfrac{2}{10}\right)=\log(2)-\log(10) =\log(2)-1\approx 0,3-1=-0,7.
\text{d. }\log\left(20\right)=\log\left(2\times 10\right)=\log(2)+\log(10) =\log(2)+1\approx 1,3.
\text{b. }\log\left(2000\right)=\log\left(2\times 1000\right)=\log(2)+\log(1000) =\log(2)+3\approx 3,3.
\text{c. }\log\left(a^{-3}\right)+\log(a^2)=-3\log(a)+2\log(a)=-\log(a).
\text{a. }\log\left(a^3\right)=3\log(a).
\text{d. }\log\left(10a^5\right)=\log\left(10\times a^5\right)=\log(10)+\log(a^5) =1+5\log(a).
\text{b. } \log (a^5)-\log(a^2)=5\log(a)-2\log(a)=3\log(a).
\text{a. }\log\left(\dfrac{1}{a}\right)=-\log(a).
\text{b. }\log\left(\dfrac{1}{a^2}\right)=-\log(a^2) =-2\log(a).
\text{c. }\log\left(\dfrac{a^5}{a^2}\right)=\log(a^3) =3\log(a).
\text{d. }\log\left(\dfrac{10}{a}\right)=\log(10)-\log(a) =1-\log(a).
Par définition \(x = \log(50)\).
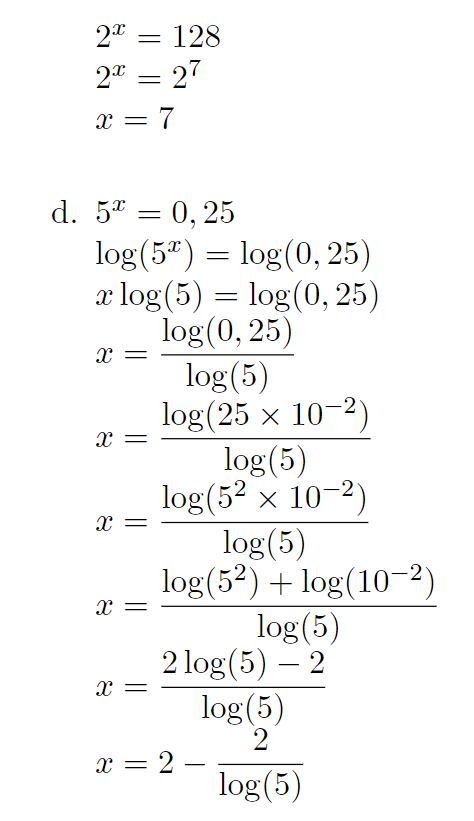
c. méthode 2 :
b_n=22000\times 1,045^n
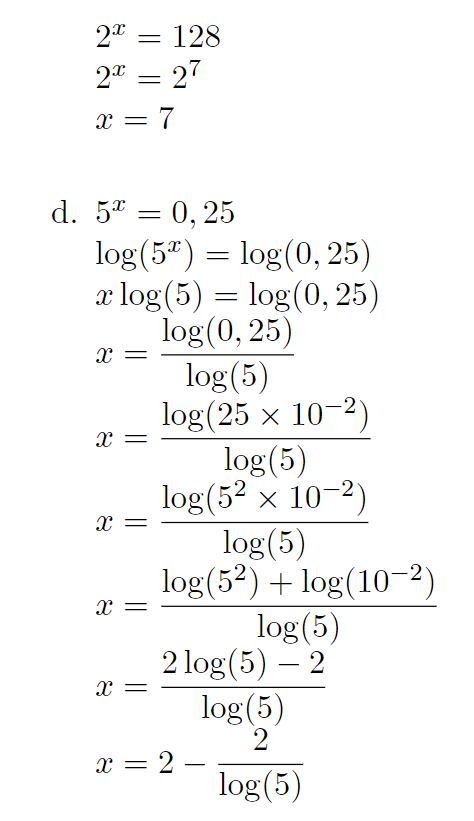
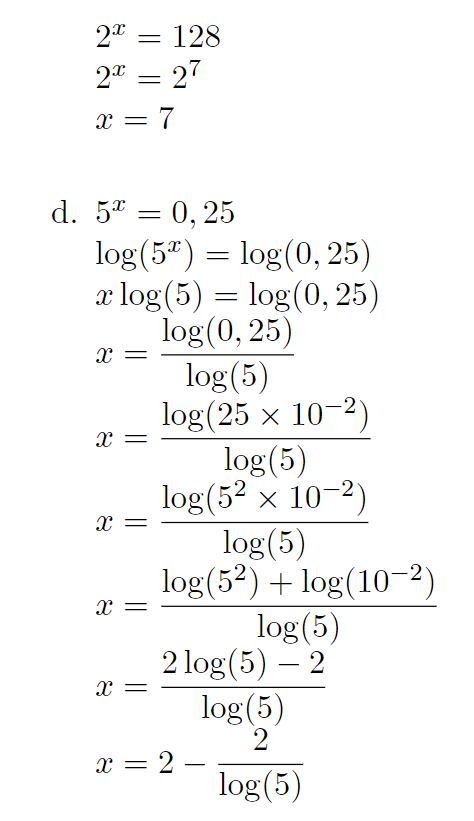
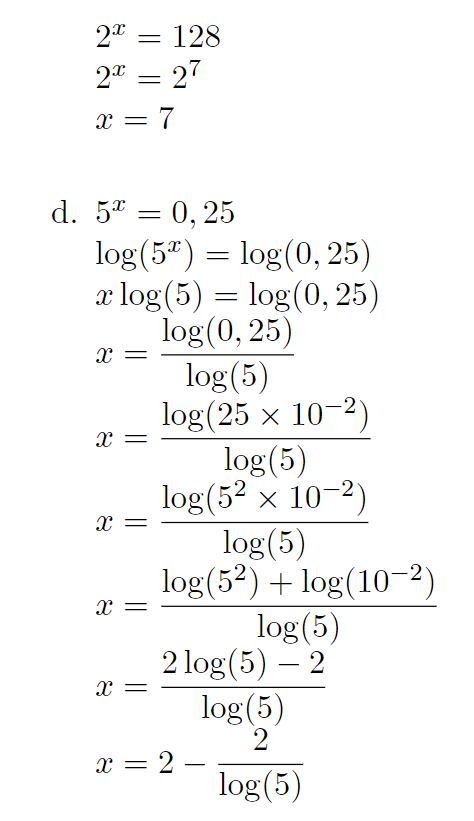
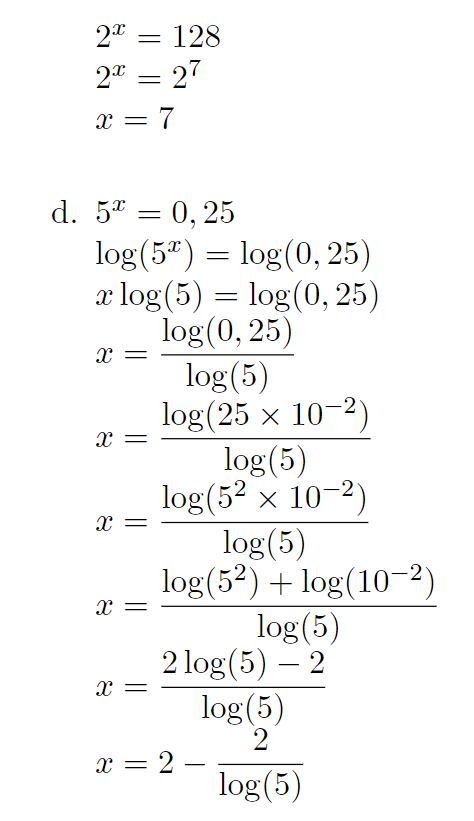
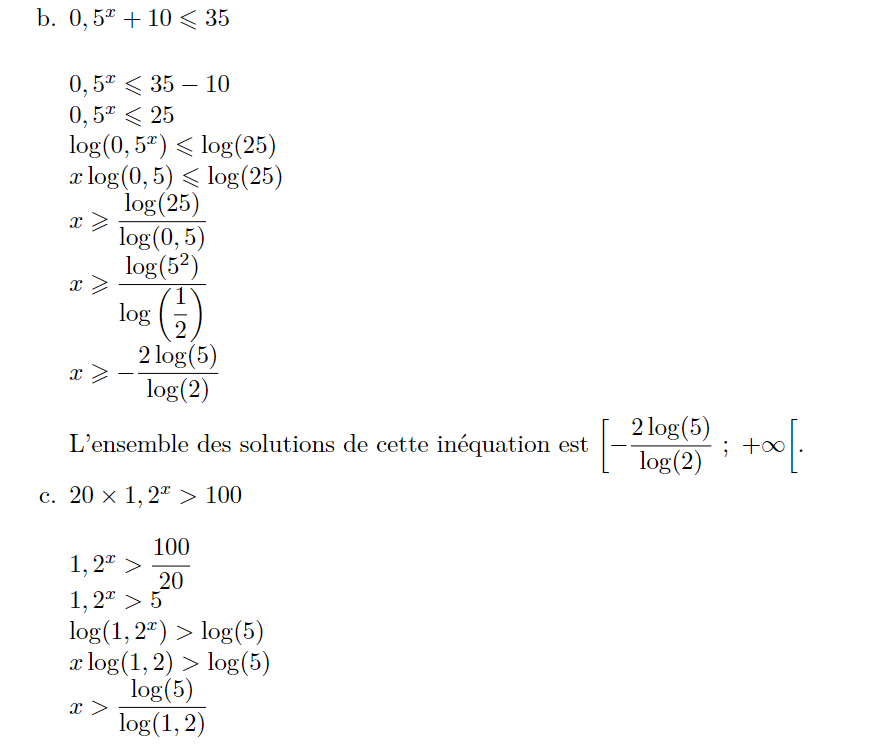
print ("le bénéfice dépassera 40 000 euros en ", A)n\geqslant \dfrac{\log(2)}{\log(1,045)}
Fonctions exponentielles de base a
By Jean-Marc Kraëber
Fonctions exponentielles de base a
Lycée Saint-Exupéry
