Suites arithmétiques et géométriques
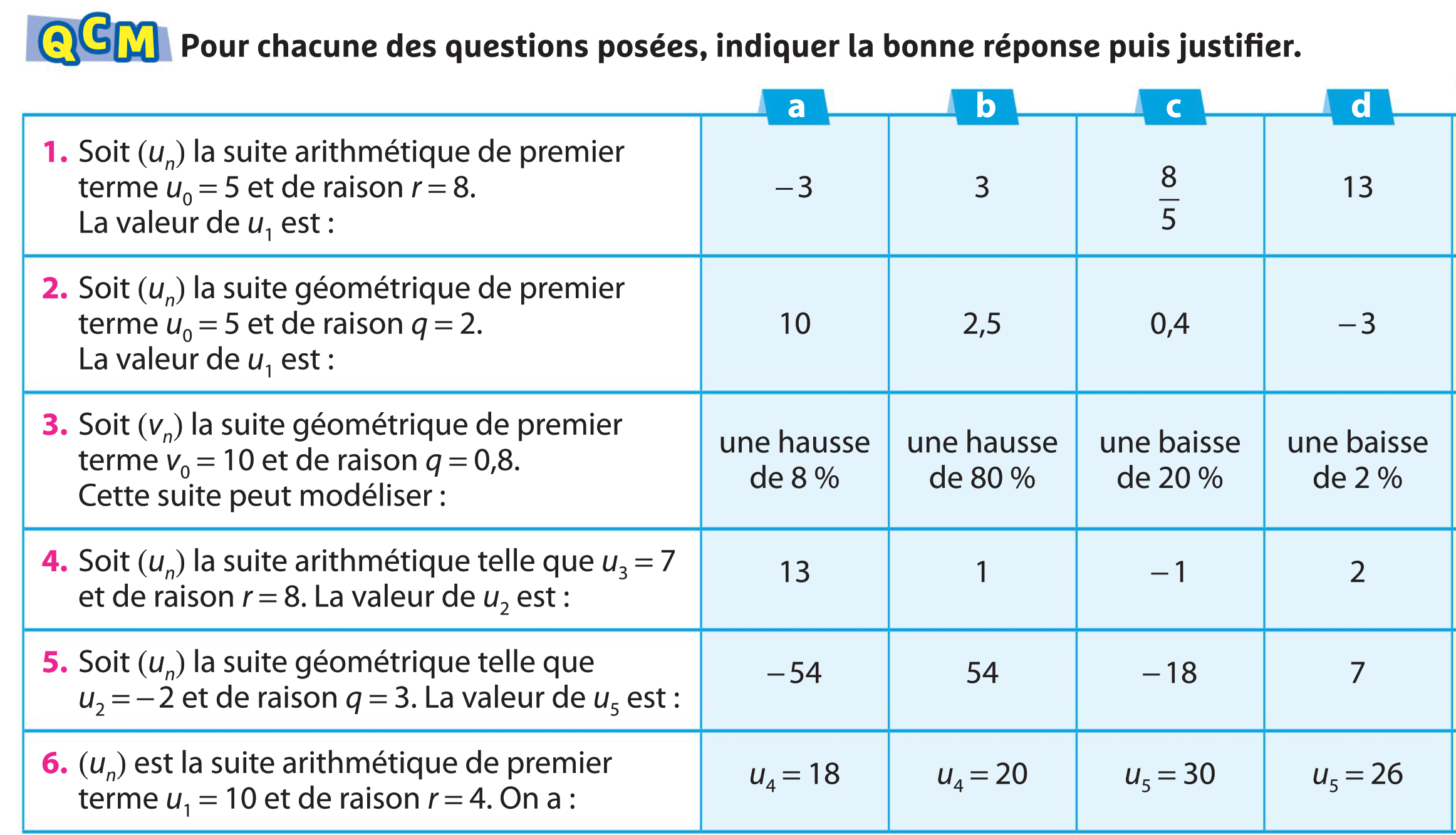
Act2 p 14
15 n = 600-300
15 n = 300
n =\dfrac{ 300}{15}
n =20
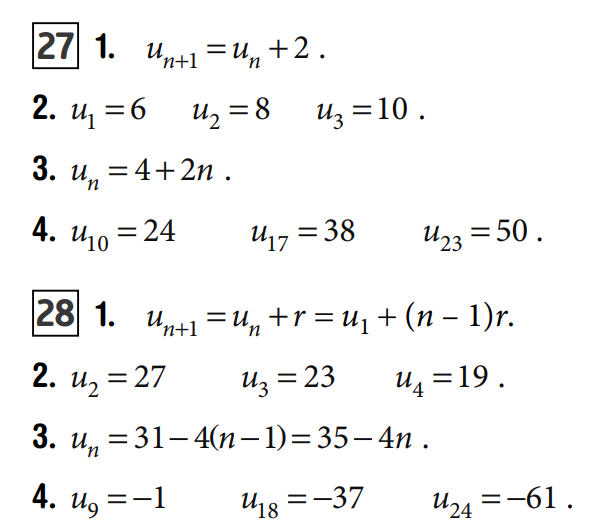
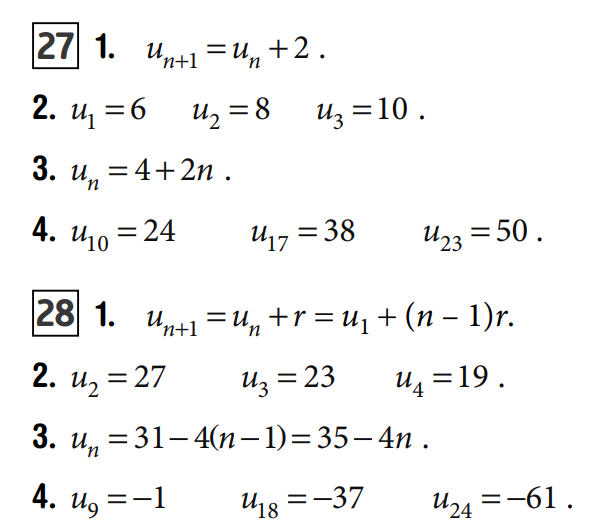
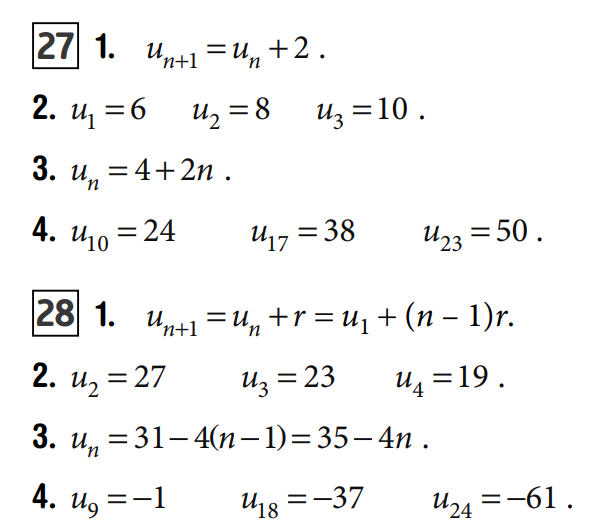
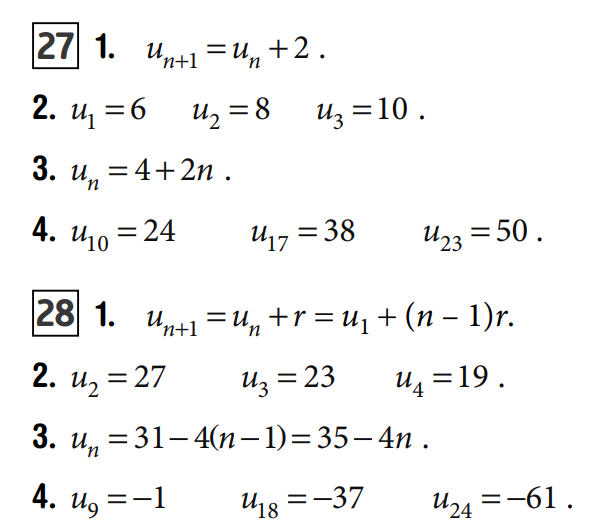
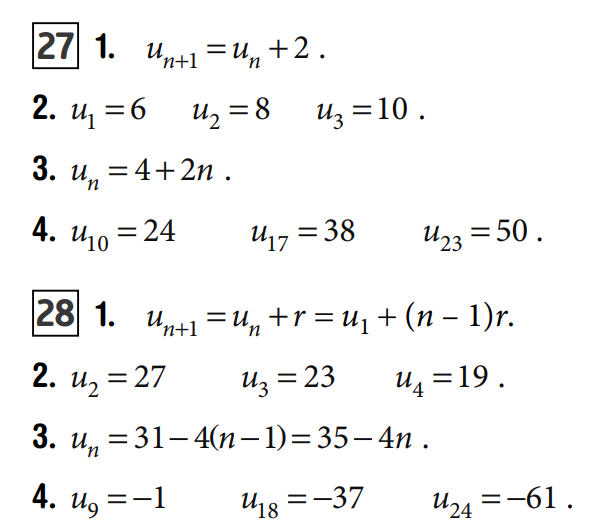
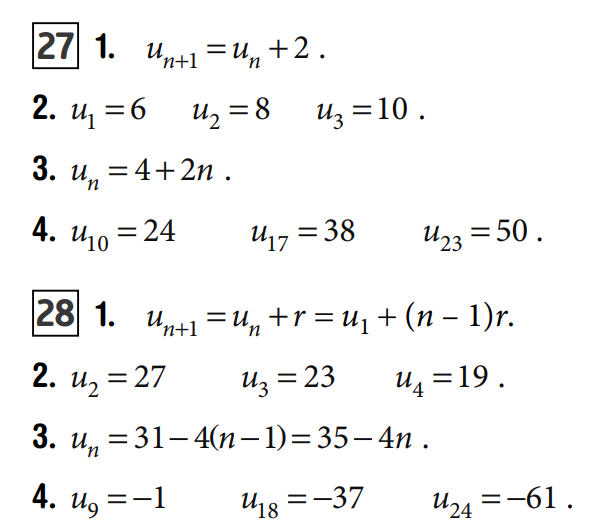
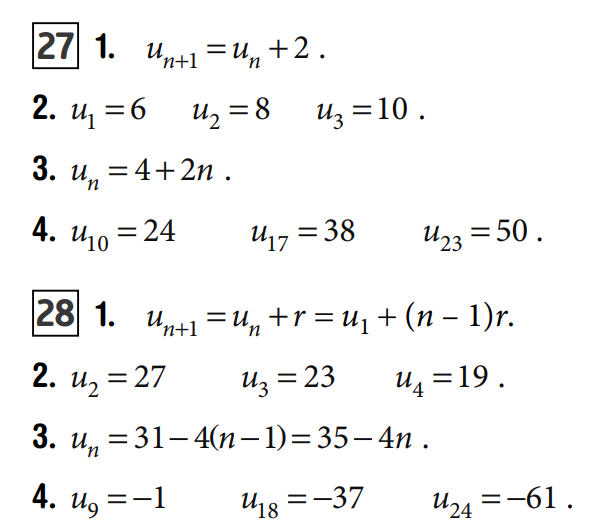
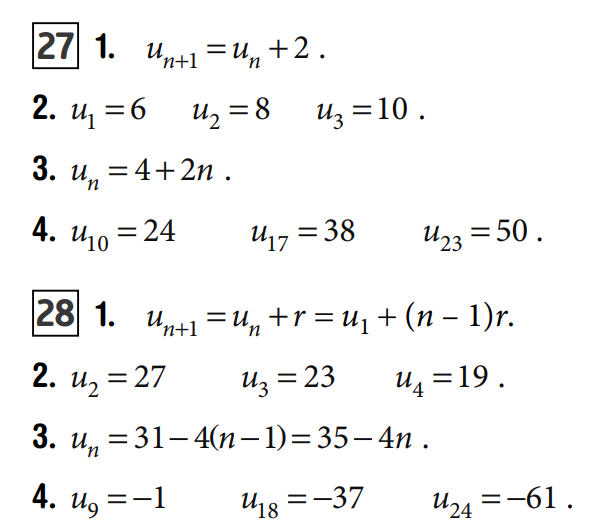
Au bout de 20 ans, Mathilde aura doublé son capital.
Avec une calculatrice Numworks
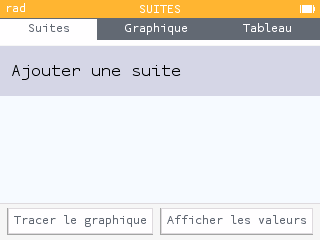
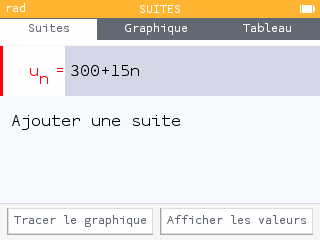
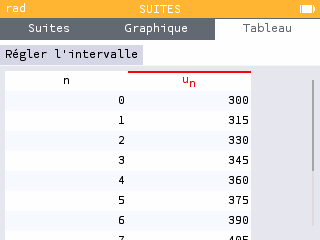
(choisir explicite)
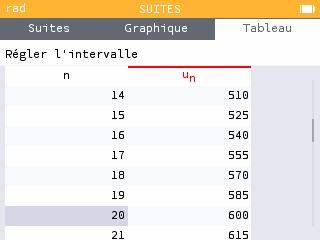
Automatismes
\dfrac{17 + x}{2}=15
17 + x=15\times 2
17 + x=30
x=30-17
x=13
17 c'est 2 points au dessus de la moyenne.
La deuxième note se situe à 2 points sous la moyenne :
15-2=13
Cette évolution peut être modélisée par une suite arithmétique de premier terme \(u_0=750\) et de raison \(r = -40\).
u_n = u_0 +n\times r
u_n = 3 +n\times 5
u_n = 3 +5n
u_n = u_1 +(n-1)\times r
u_n = 6 +(n-1)\times (-8)
u_n = 6-8n+8
u_n = 14-8n
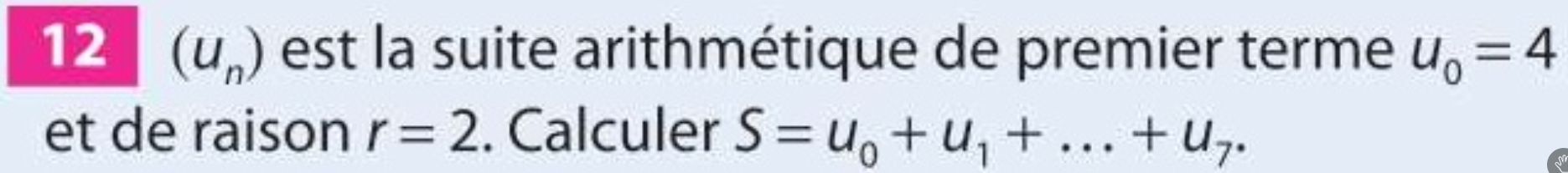
On calcule le dernier terme de la somme :
u_7 = u_0 + 7\times r=4 + 7\times 2 = 18
S = \dfrac{8\times(4 + 18)}{2}=88
cette somme contient 8 termes :
Suites géométriques
Act 3 p 15 : Un roi qui "riz"
\text{calcul : }\dfrac{2^{64}-1}{60 000000}
\text{Formule : }u_1+u_2+\dots+u_n = u_1\times \dfrac{1-q^{n}}{1-q}
\sqrt{4\times 16}=\sqrt{64} = 8
\text{On a donc }u_{n+1}=1,01\times u_n
Tant que U < 450
N N+1
U \(1,054 \times U\)
A la calculatrice, on obtient n = 8 :
u_8\approx 456,93
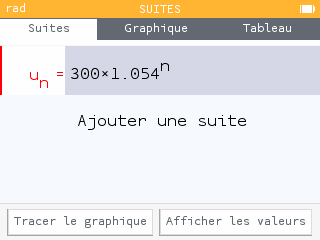
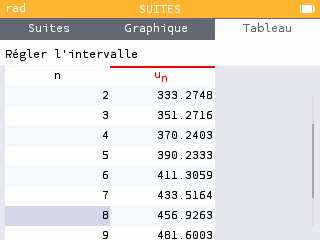
Donc après l'exécutionde cet algorithme
N = 2017 + 8 = 2025 et \( U\approx 456,93 \).
Automatismes : Suites
7\times 2 = 14
14\times 2 = 28
Les trois nombres proposés sont les trois premiers termes d'une suite géométrique de raison 2.
20\times (-0,5) = -10
-10\times (-0,5) = 5
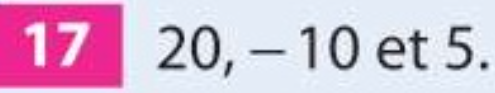
Les trois nombres proposés sont les trois premiers termes d'une suite géométrique de raison \(-0,5\).
L'évolution proposée est modélisée par une suite géométrique de premier terme \(u_0=450 000\) et de raison \(q=0,94\).
1-0,06 = 0,94
L'évolution proposée est modélisée par une suite géométrique de premier terme \(u_0=50 000\) et de raison \(q=1,15\).
1+0,15 = 1,15
u_n = 2\times 3^n
u_n = 4\times 0,5^{n-1}
S = 4\times \dfrac{1-2^{12}}{1-2}=16380
S = 10\times \dfrac{1-7^{10}}{1-7}=470792080
\text{On a }d_{n+1}=1,06\times d_n
57 p 26 - 27
S=21\times \dfrac{1-3^7}{1-3}=22953
u_9=20000\times 0,85^9\approx 4632
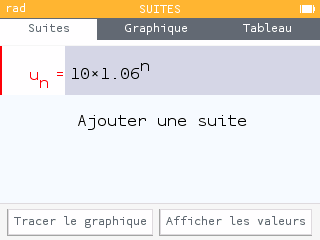
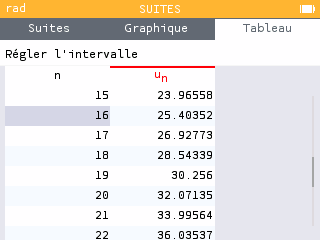
Selon ce modèle 4632 mégots seront jetés en 2028.
En 10 ans, 107 083 mégots auront été ramassés.
107\,083
v_n=125\times 1,03^n
A la calculatrice on obtient :
Corrigé des automatismes n°2
- 21
- 44
- 6
- 40
- \(u_n=2+5n\)
- \(u_5=27\)
- \(u_n=8+3(n-1)=5+3n\)
- \(u_7=26\)
- 8
- \(u_7=3+4\times 7=31\) et \(\dfrac{(3+31)\times 8}{2}=136\)
11) 10
12) \(u_{10}=7+9\times (-2) =-11 \)
13) \(u_n=3\times 2^n\)
14) \(u_5=3\times 2^5=96\)
15) \(u_n=-2\times 3^{n-1}\)
16) \(u_3=-2\times 3^2=-18\)
17) 8
18) \(\dfrac{1-2^8}{1-2}=255\)
19) 6
20) \(4\times \dfrac{1-(-2)^6}{1-(-2)}=-84\)
Suites arithmétiques et géométriques
By Jean-Marc Kraëber
Suites arithmétiques et géométriques
Lycée Saint-Exupéry
