Conditionnement


1200
800
2000
1987
13
b.\;\dfrac{13}{2000}
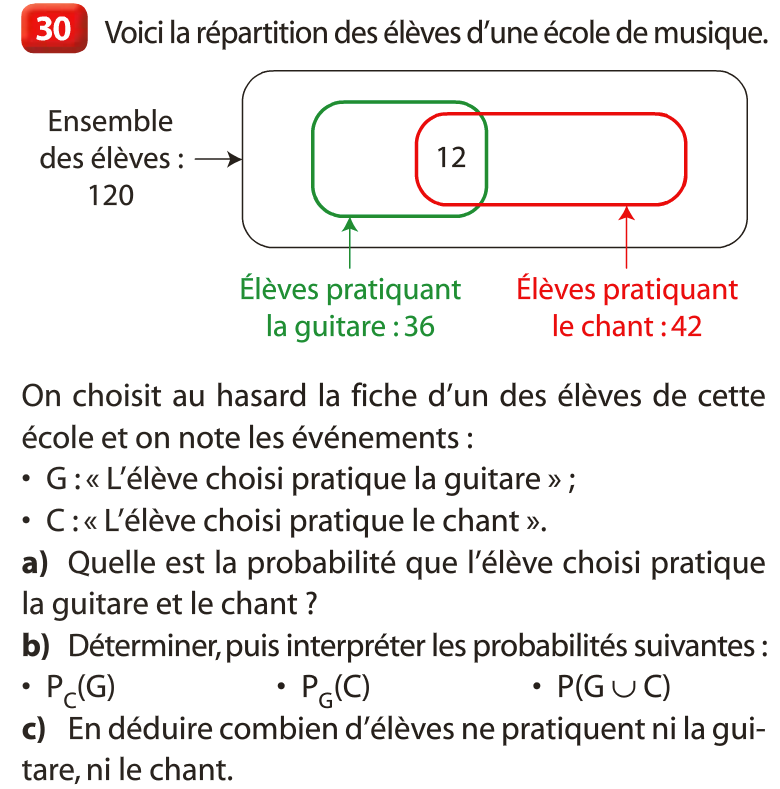
c.\;\dfrac{12}{1200}\text{ est la proportion de joueurs gagnants}
\text{parmi les joueurs du jeu A.}
\dfrac{12}{13}\text{ est la proportion de joueurs du jeu A parmi les gagnants.}

Une variable aléatoire associe aux issues d'une expérience aléatoire des nombres réels.
A chaque valeur prise par la variable aléatoire est associée une probabilité : c'est la loi de probabilité de la variable aléatoire.
Les valeurs prises par la variable aléatoire sont : -2, 3, 8, 18 et 48.
| -2 | 3 | 8 | 18 | 48 | |
|---|---|---|---|---|---|
x_i
p_i
\frac{376}{400}
\frac{10}{400}
\frac{8}{400}
\frac{5}{400}
\frac{1}{400}

b)\;E(X) = p_1x_1+p_2x_2+\;...\;+p_nx_n
c)\;E(x)\neq 0 \text{ donc le jeu n'est pas équitable.}
E(x)<0 \text{ donc le jeu est défavorable au joueur .}
= -2\times \frac{376}{400}+3 \times \frac{10}{400}+8\times \frac{8}{400}+18\times \frac{5}{400}+48\times \frac{1}{400}
= -1,3

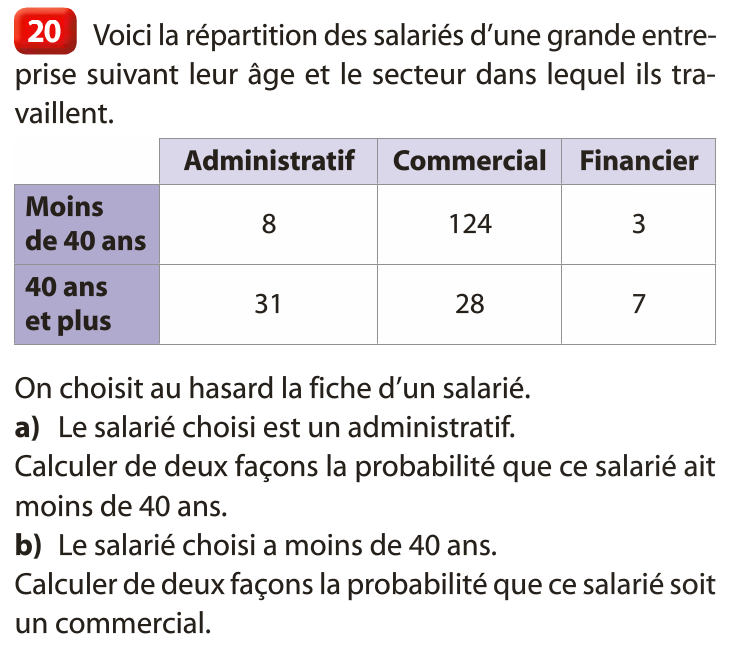




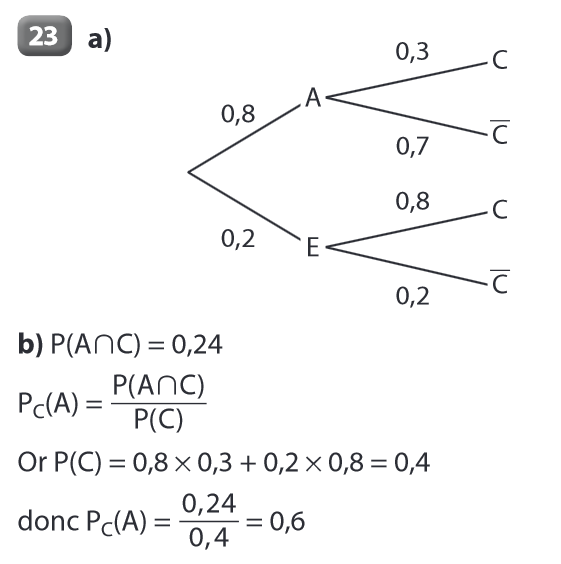
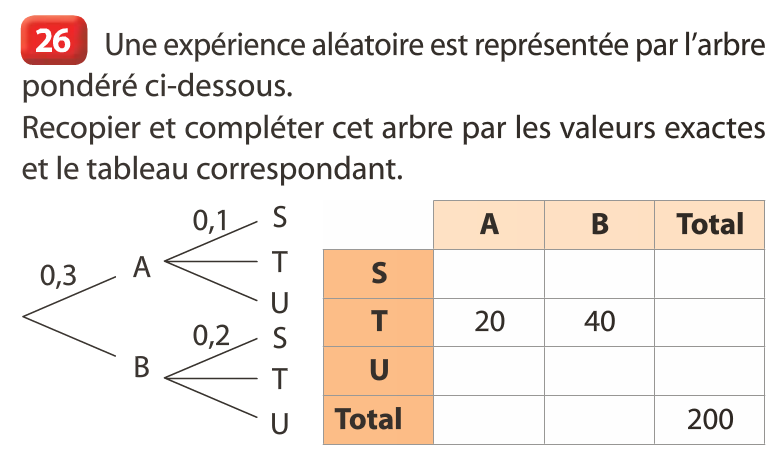
p(A) = 0,3 = \dfrac{60}{200}
p_A(S) = 0,1\;donc\;\dfrac{p(S\cap A)}{0,3}=0,1
\Leftrightarrow p(S\cap A) = 0,03 = \dfrac{6}{200}.
p_B(S) = 0,2\;donc\;\dfrac{p(S\cap B)}{0,7}=0,2
\Leftrightarrow p(S\cap B) = 0,14 = \dfrac{28}{200}.
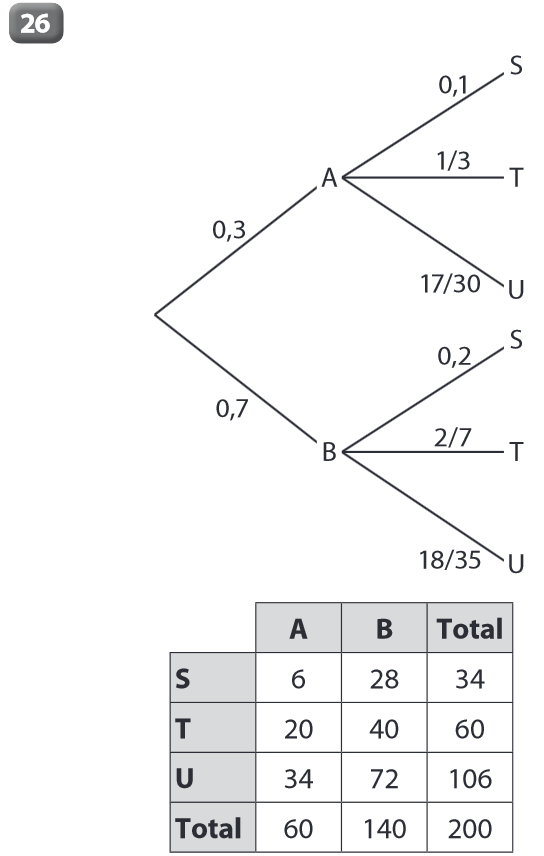

p_A(T) = \dfrac{20}{60}=\dfrac{1}{3}
p_B(T) = \dfrac{40}{140}=\dfrac{2}{7}



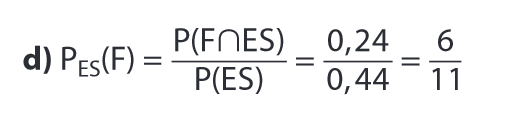
Conditionnement
By Jean-Marc Kraëber
Conditionnement
Terminale ES
- 1,253



