Fonctions exponentielles
Act. 1 p 39 Hyperbole 2012 (Nathan)
Cours : Les fonctions \( x\rightarrow q^x \)
37, 38, 39, 40, 42, 45, 46, 44 p 48 - 47 p 49
Cours : La fonction \( x\rightarrow e^x \)
48 à 55 p 49
Étude de la fonction \( x\rightarrow xe^x \)
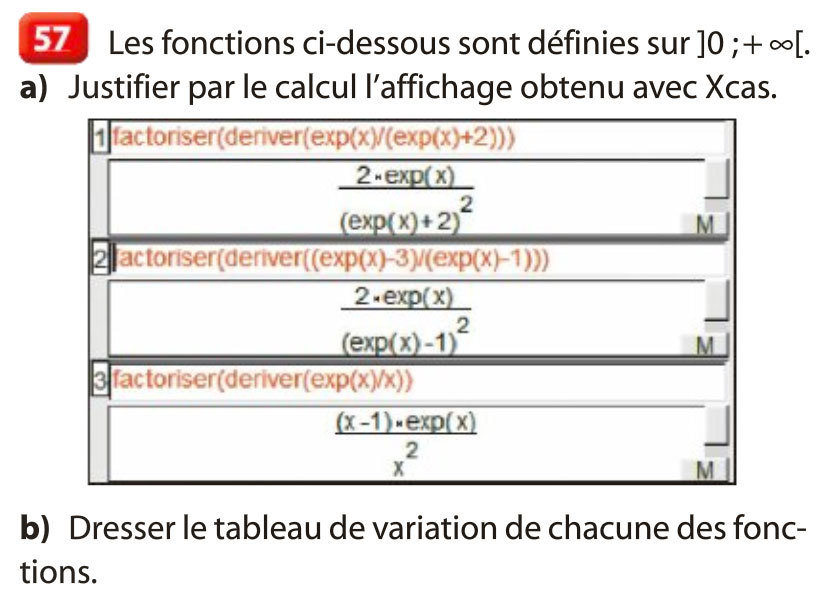
56 à 58 p 49 - 60 p 50
Cours : Fonctions \( x\rightarrow e^{u(x)} \)
63, 64, 65 p 50 - 68 p 51 - 61, 62 p 50 - 83 p 55



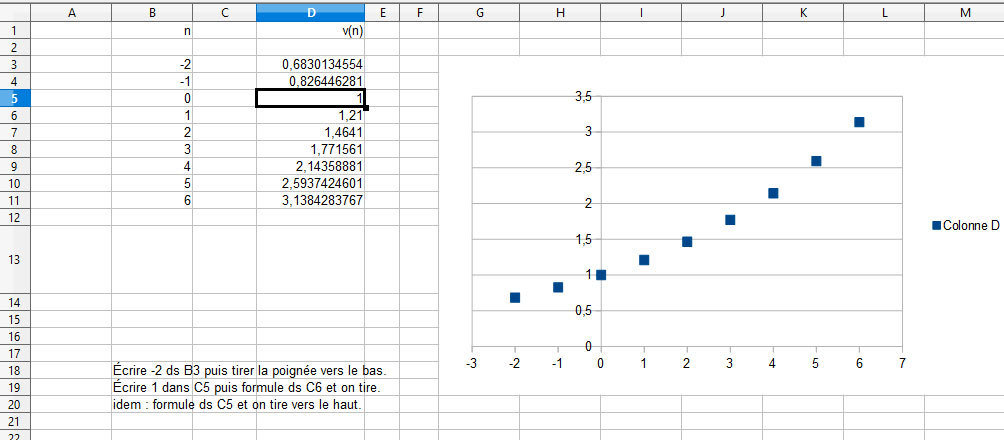
2 b)
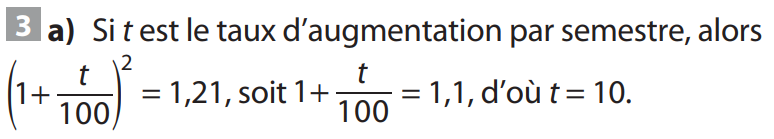
Le taux d’augmentation pour un semestre est 10 %.

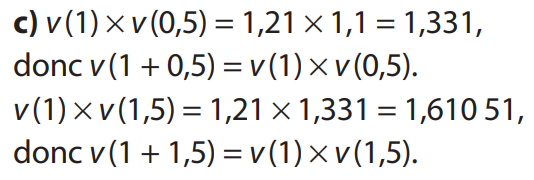
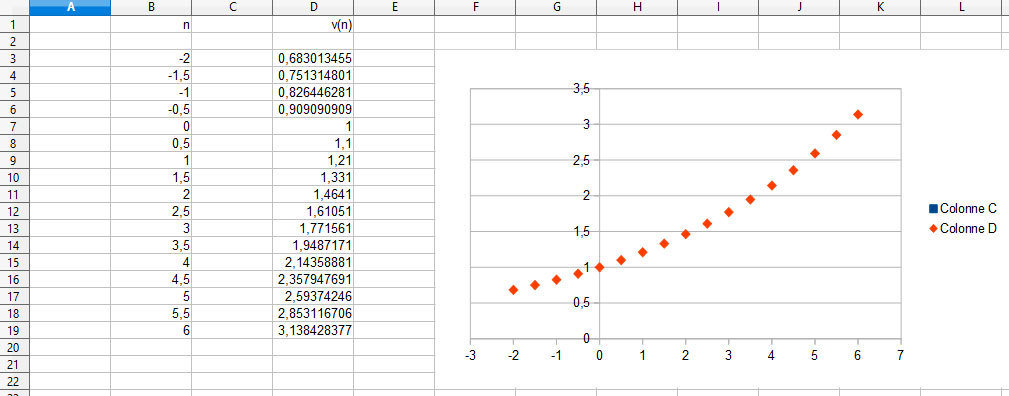
3 d)

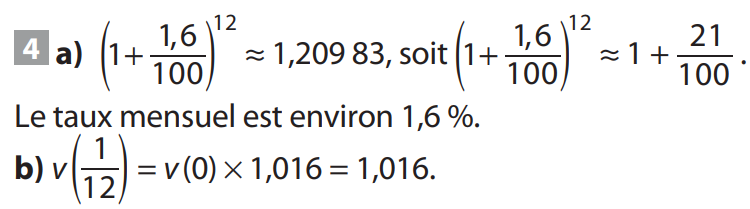
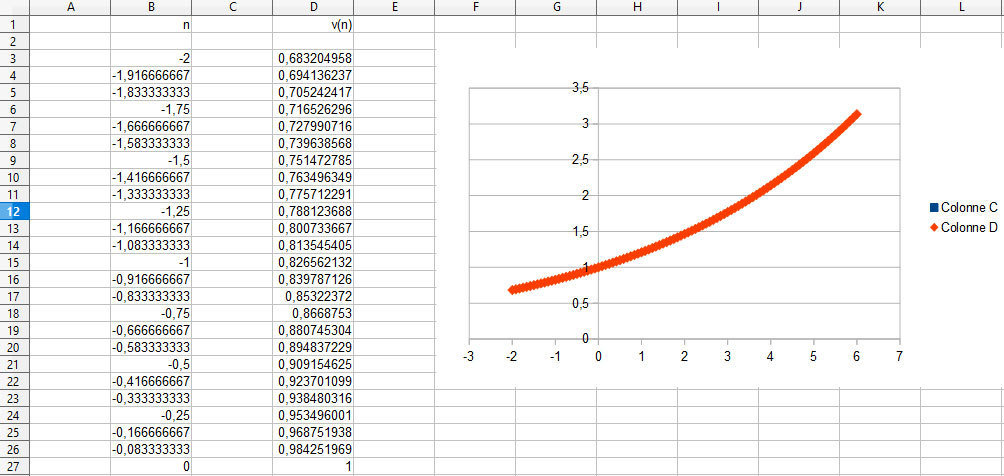
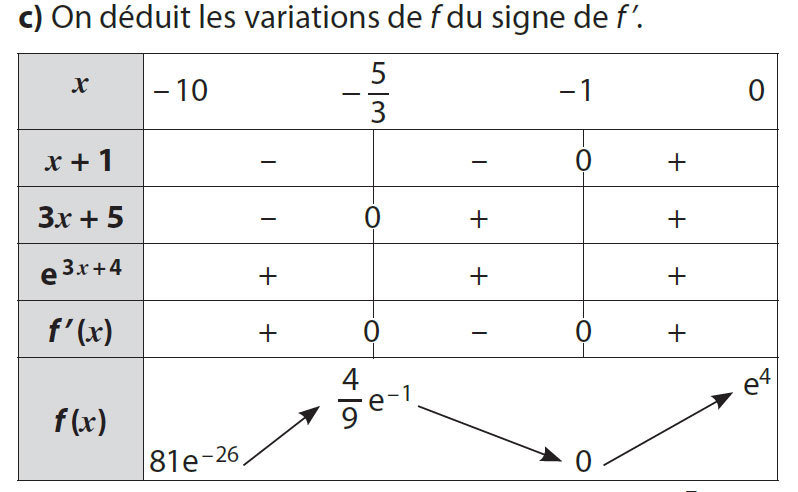
4 c)
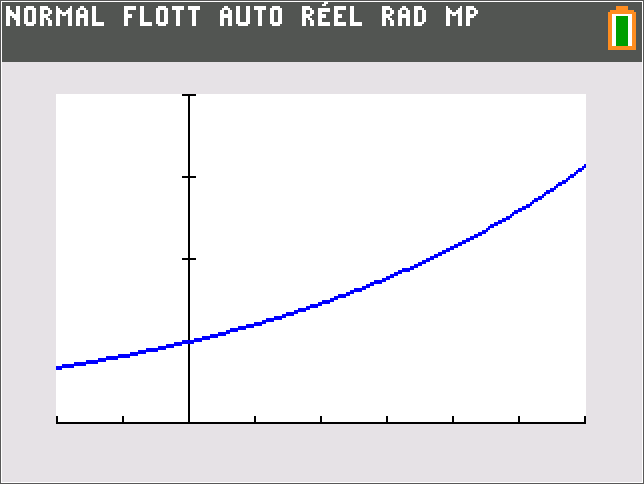
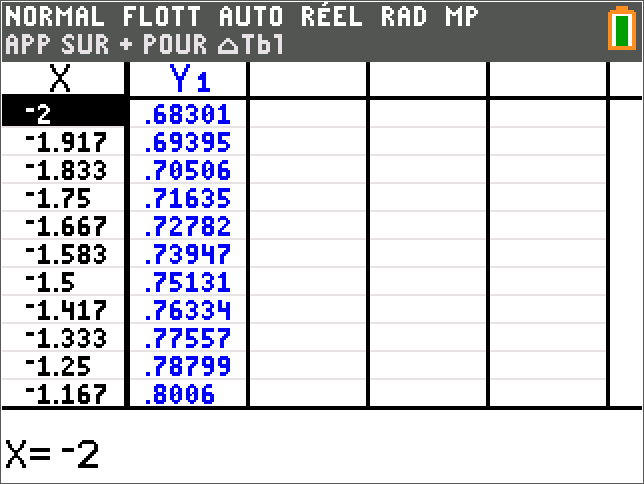
5)
Fonctions exponentielles
1.1 Fonction exponentielle de base q

Théorème - Définition : (admis)
Remarque : On utilise la calculatrice pour calculer des images par ces fonctions. Par exemple, l’image de 2,3 par la fonction exponentielle de base 1,21 est
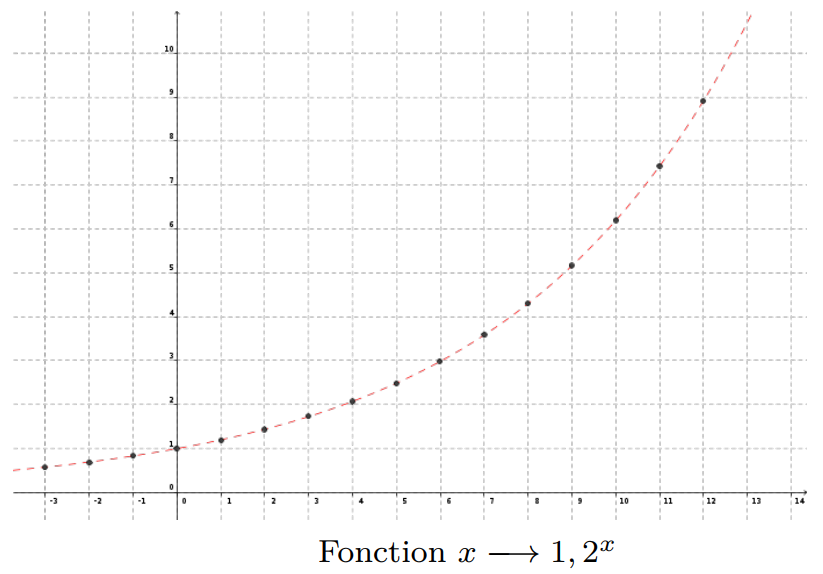
Exemples :
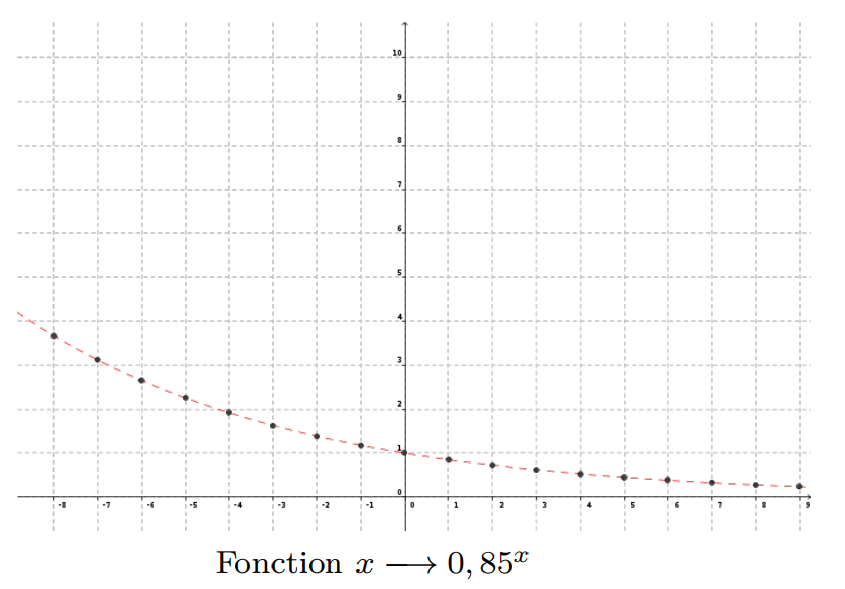
1.2 Sens de variation
Propriété :
Conséquence : Si 𝑞 ≠ 1, alors pour tous nombres réels a et b :
Comme la fonction exponentielle de base q est un prolongement continu de la suite géométrique , son sens de variation est le même que celui de cette suite :

1.3 Conséquences de la relation fonctionnelle
Théorème : Pour tout nombre réel x, on a
Rappel : Soit 𝑞 > 0 et x, y deux réels. Alors :
Démonstration :
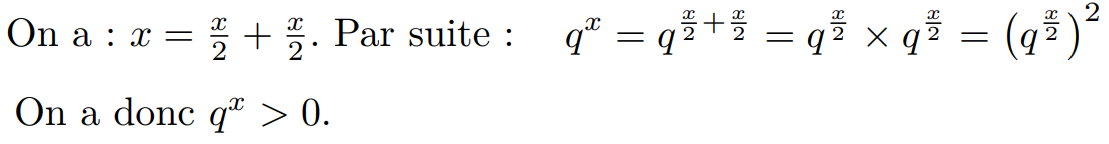
Théorème : Soient q > 0, x et y deux réels.

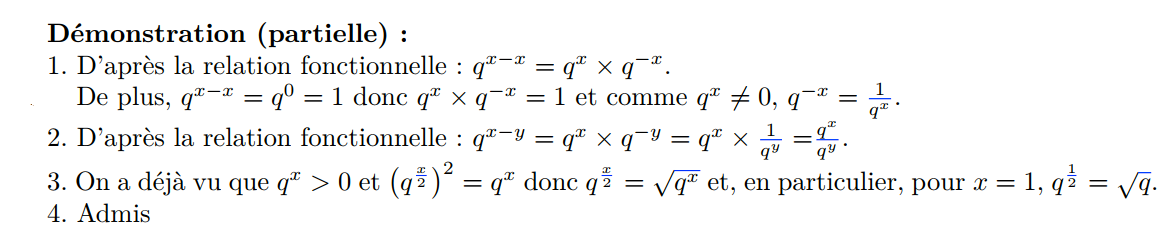
Remarque :
- On retrouve des propriétés similaires à celles des puissances.
- Le point 3. se généralise : pour q > 0 et n entier naturel non nul, on peut vérifier que est le nombre positif qui, élevé à la puissance n donne q. On dit que c’est la racine n-ième de q et on note :


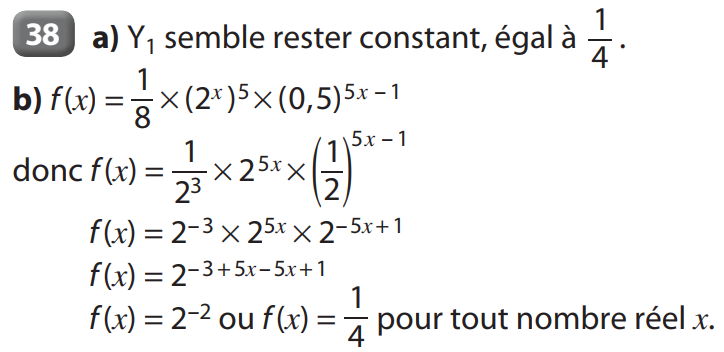

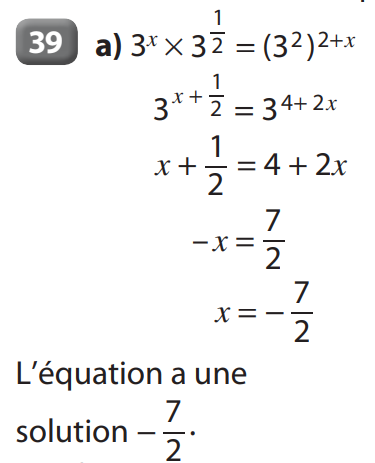
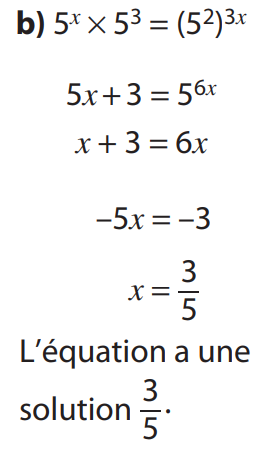

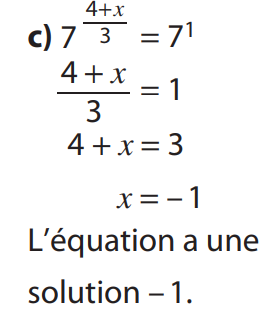
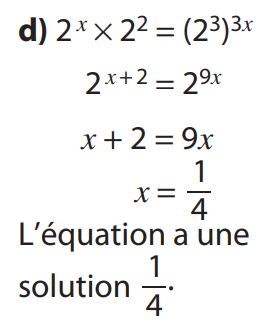







2.1 Définition – premières propriétés
Théorème - Définition : (admis)
Remarque : à la calculatrice, on obtient

Propriété : La fonction exponentielle est strictement croissante sur R.
Remarque : Il suffit d’appliquer la propriété du 1.2 avec
On en déduit le résultat suivant :
Propriété : Pour tous réels a et b, on a :
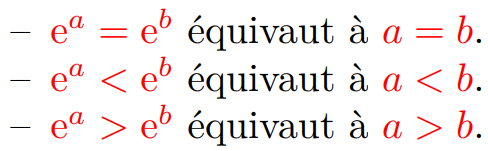
Remarque : En particulier, comme
2.2 Dérivée – Courbe représentative
Propriété : (admise) La fonction exponentielle est dérivable sur R et sa dérivée est égale à elle-même. On a donc :
Démonstration :

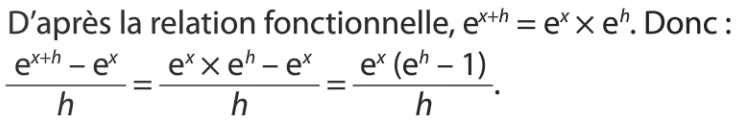

Remarques :
- On a déjà vu que . La dérivée de la fonction exponentielle est donc strictement positive. On retrouve le fait que la fonction exponentielle est strictement croissante sur R.
- On peut alors donner le tableau de variations de la fonction exponentielle.
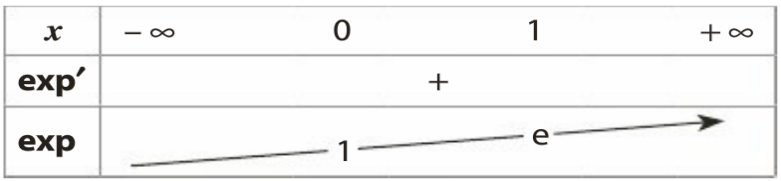
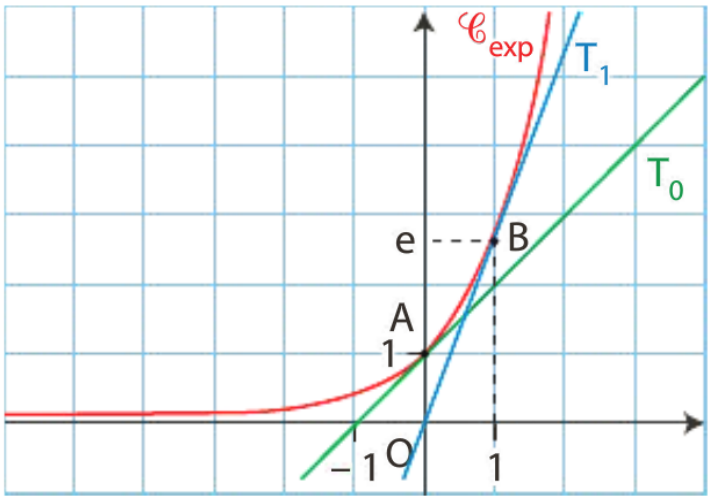
3. On peut alors construire la courbe représentative de la fonction exponentielle à l’aide d’un tableau de valeurs en remarquant que chaque résultat trouvé correspond non seulement à l’ordonnée du point de la courbe mais aussi au coefficient directeur de la tangente car (exp)'=exp.
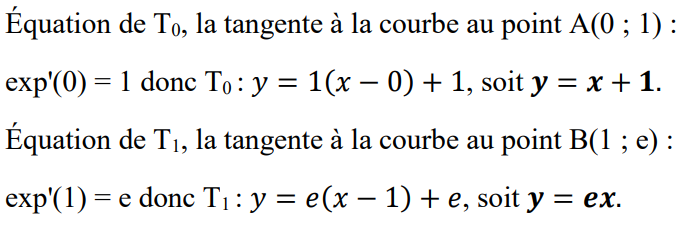

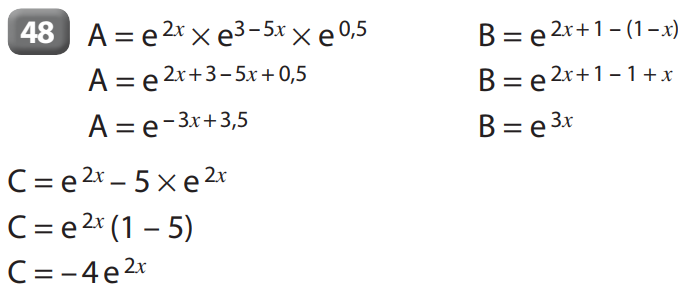
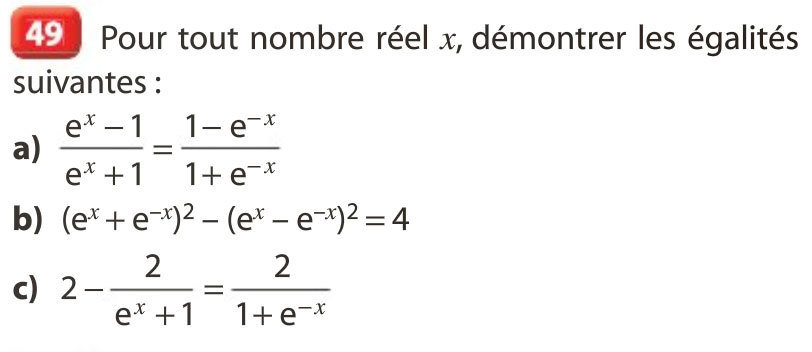
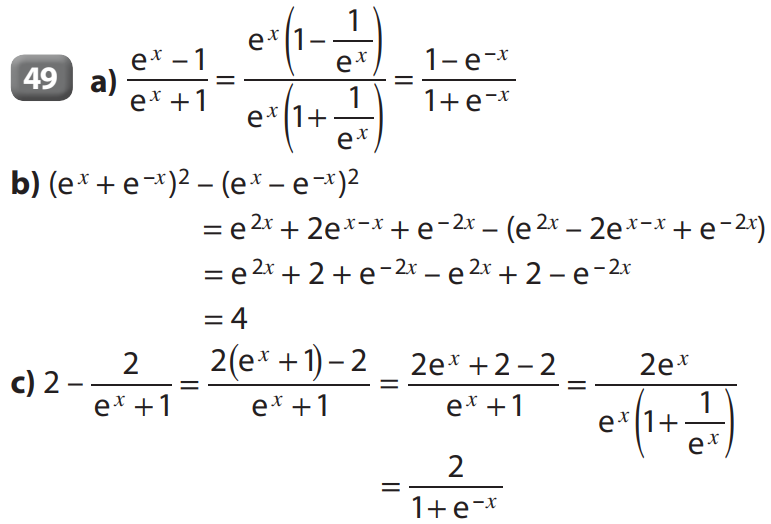
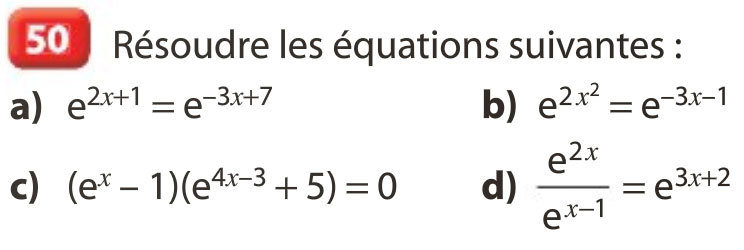
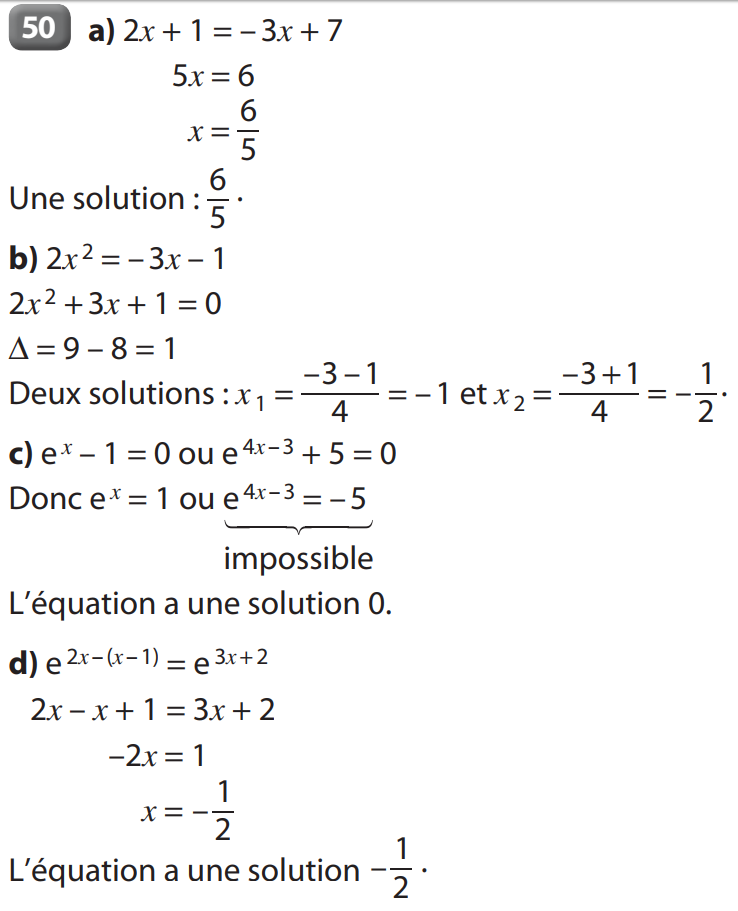



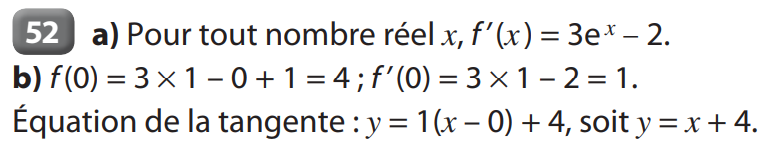






Étude de la fonction \(f:x\rightarrow xe^x\)
f est définie sur ]\( -\infty ; +\infty \)[.
f est le produit de deux fonctions dérivables sur ]\( -\infty ; +\infty \)[ donc f est dérivable sur ]\( -\infty ; +\infty \)[.
Calcul de la dérivée : f est de la forme uv avec \(u(x)=x\) et \(v(x)=e^x\).
On a \(u'(x)=1\) et \(v'(x)=e^x\).
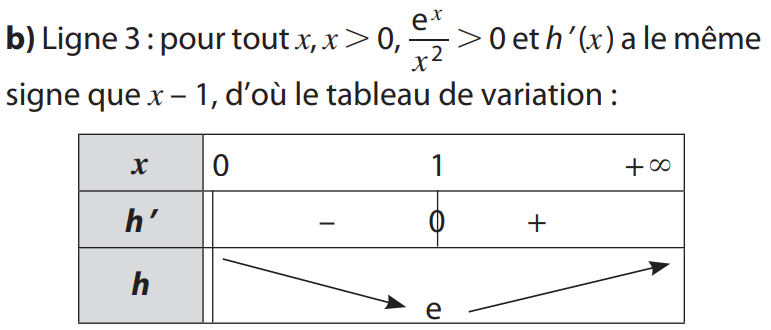
Pour les variations de \(f\) : On étudie le signe de la dérivée \(f '\)
On factorise :
Dérivée d'un produit : \((uv)'=u'v+uv'\)
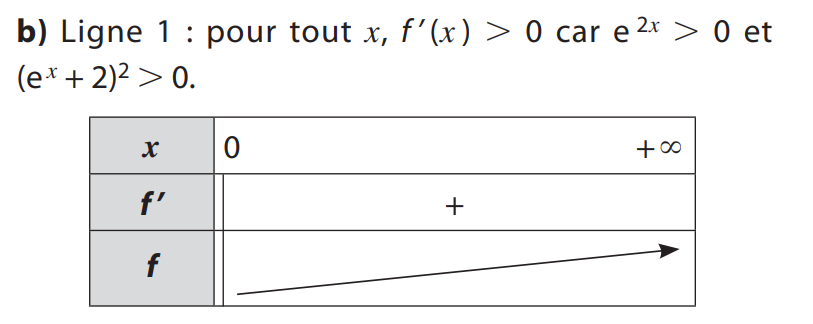
Pour tout réel x, \( e^x > 0 \) donc
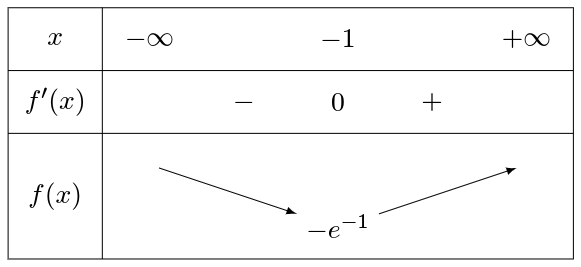
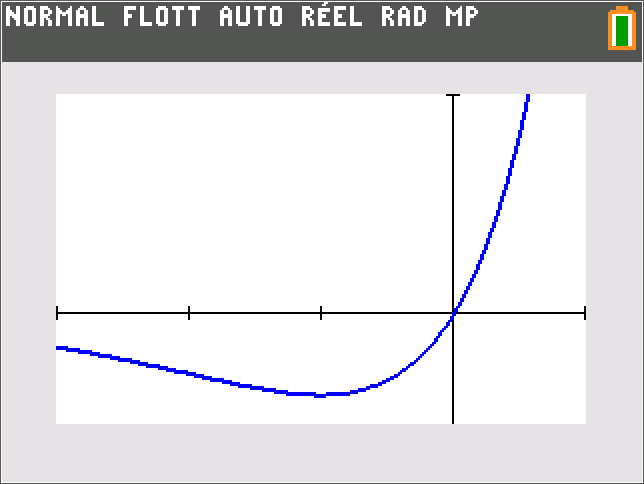
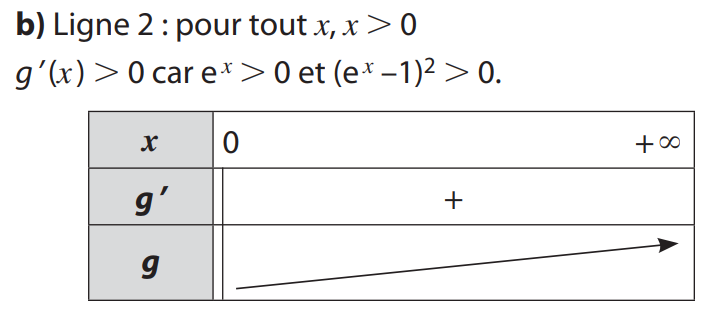
Tableau de variations de f :

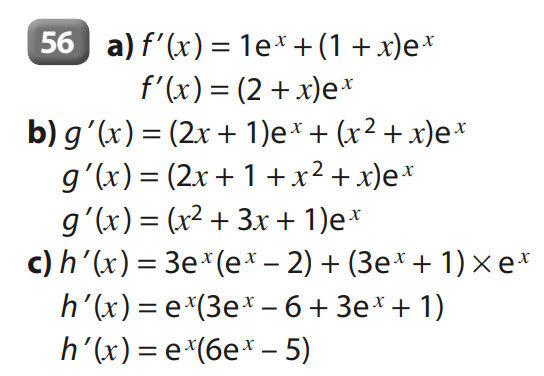
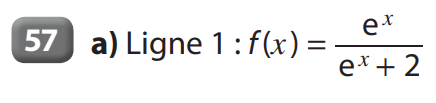
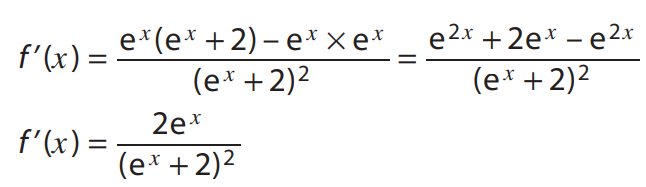
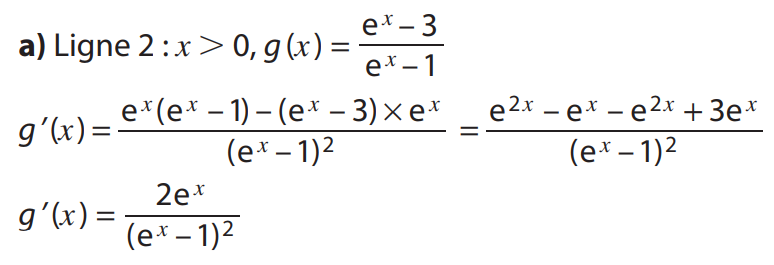
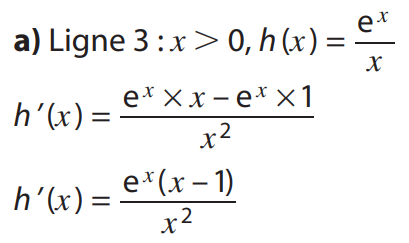





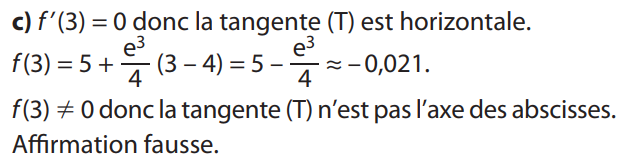
2.3 Fonctions \(x\rightarrow e^{u(x)}\)
Propriété : Soit u une fonction dérivable sur un un intervalle I.
Alors la fonction f définie sur I par \(f(x) = e^{u(x)}\) est dérivable sur I et : \(f'(x) = u'(x)e^{u(x)}\)
Remarque : En particulier, comme l’exponentielle est strictement positive, f' est du même signe que u'.
Exemples :

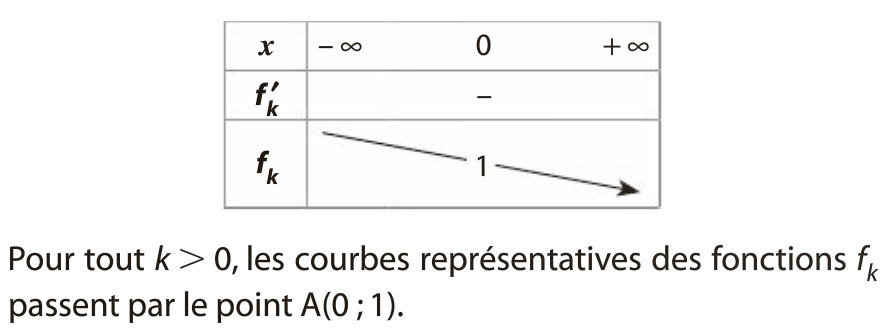
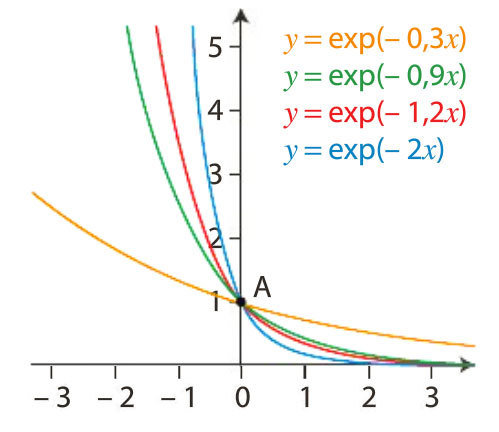


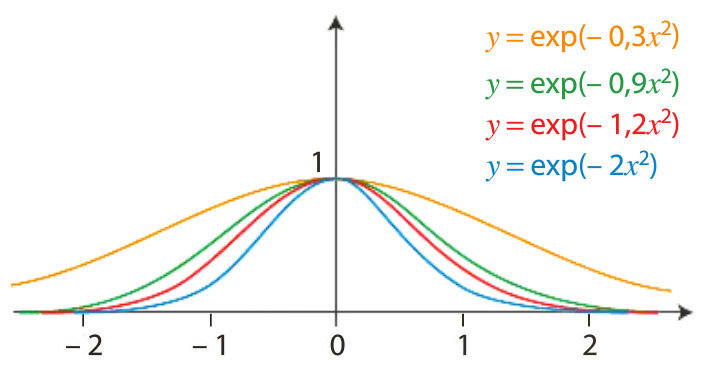

a) f est de la forme uv avec \(u(x)=3x-1\) et \(v(x)=e^{-2x}\).
Dérivée d'un produit : \((uv)'=u'v+uv'\)
On a \(u'(x)=3\) et
Dérivée de \(e^u\) : (\(e^u\))' = \(u'e^u\)
puis on factorise...
b) g est de la forme \(e^u\) avec \(u(x)=\frac{1}{2}x^2-3\)
On a \(u'(x)=x\).
h) h est de la forme \(\frac{1}{u}\) avec \(u(x)=2+e^{-3x}\)
On a \(u'(x)=-3e^{-3x}\)
Dérivée de \(e^u\) : (\(e^u\))' = \(u'e^u\)
Dérivée de \(\frac{1}{u}\) : (\( \frac{1}{u}\))' = \(- \frac{u'}{u^2}\)

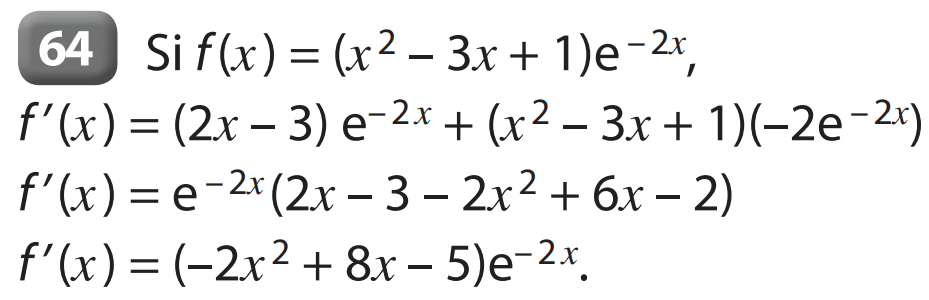
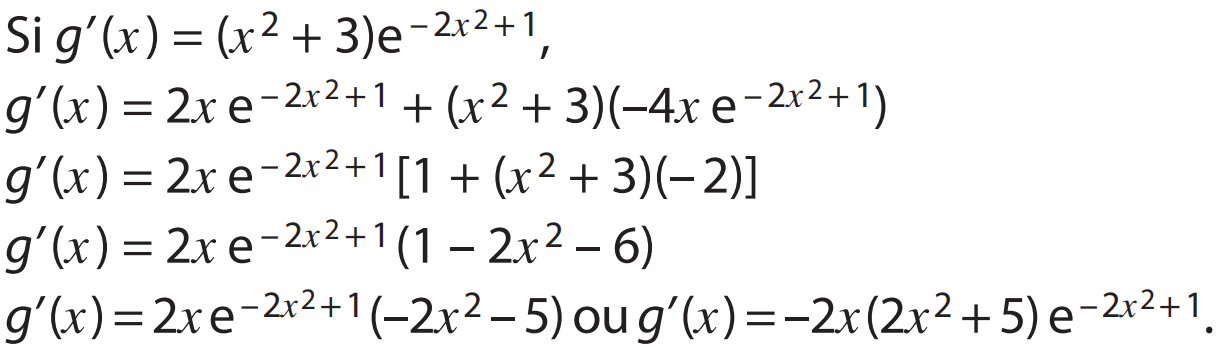

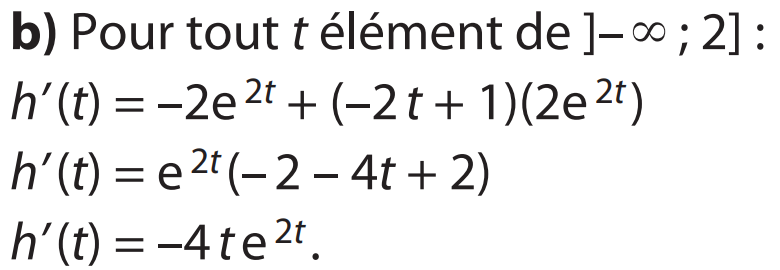
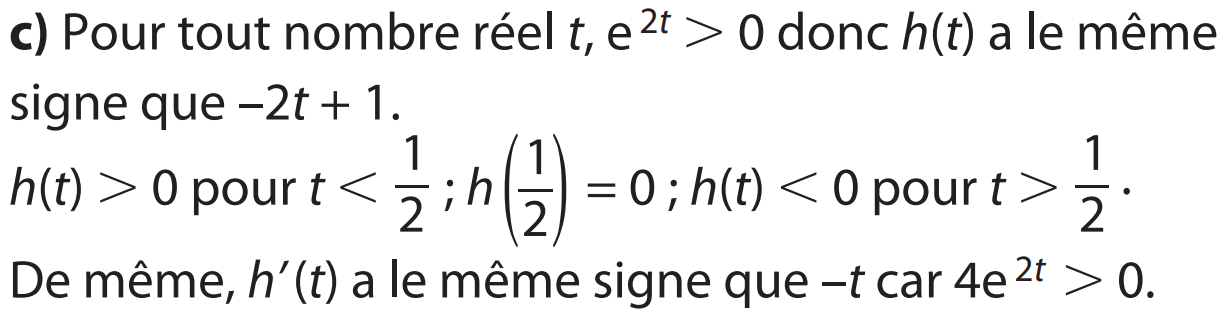
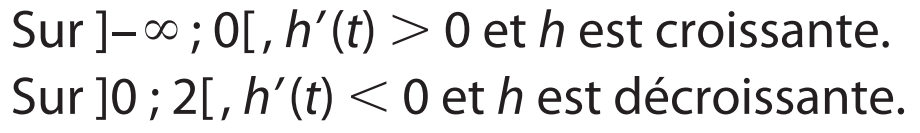

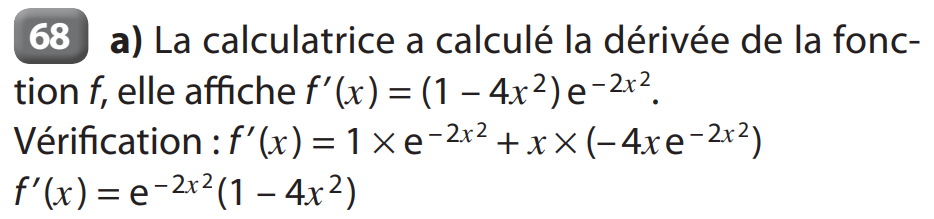




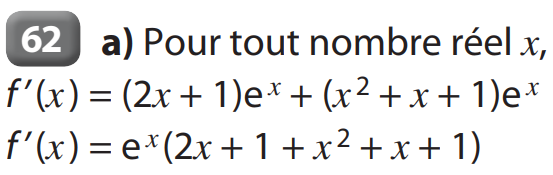
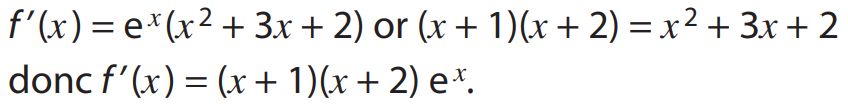
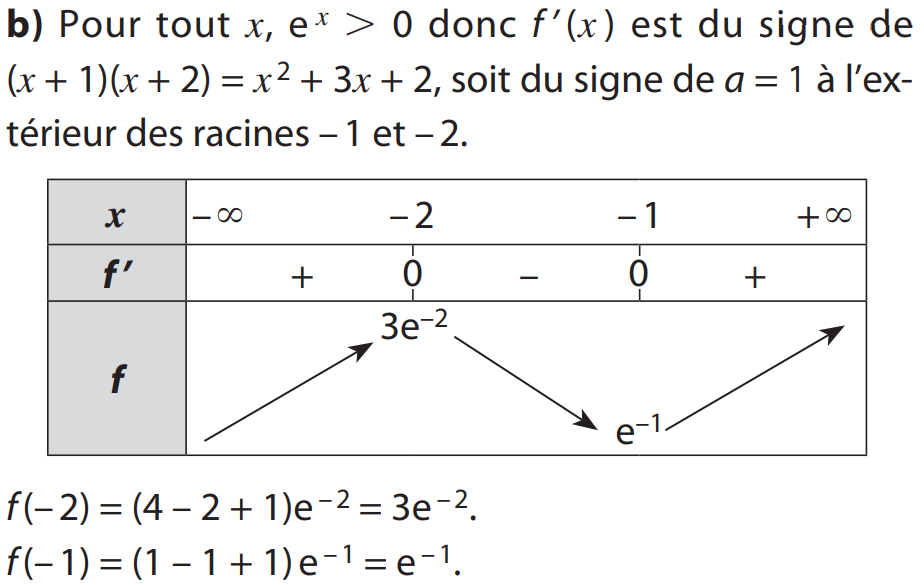
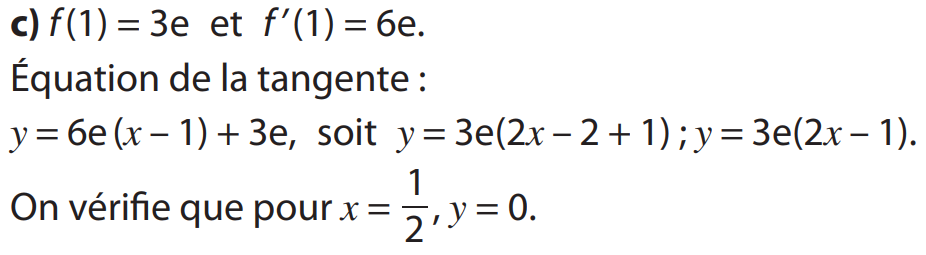

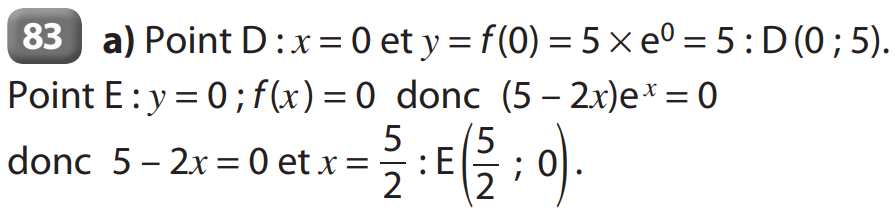
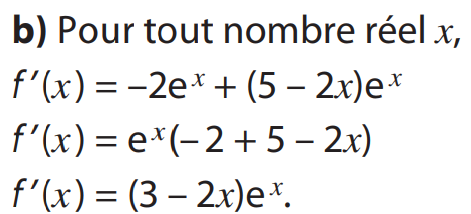
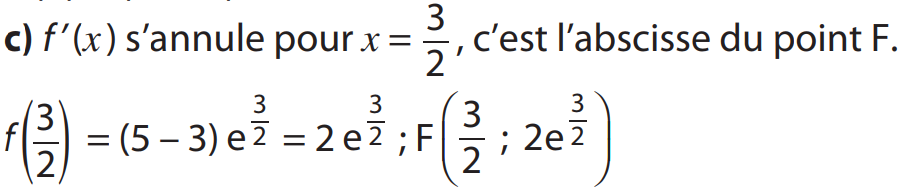


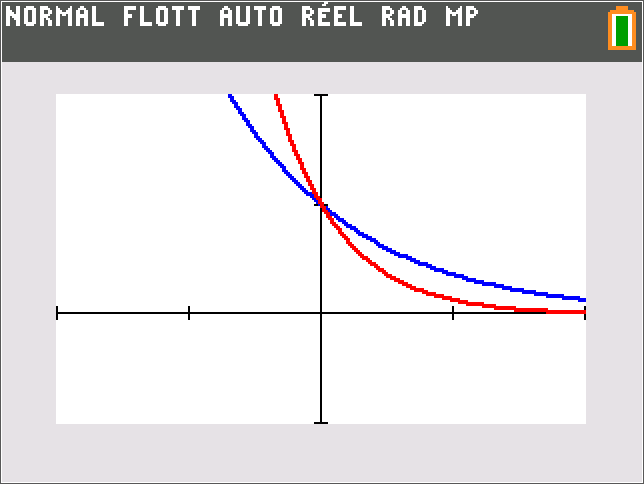
Méthode : Pour étudier les positions relatives de deux courbes Cf et Cg, on étudie le signe de \( f - g \) ou si les fonctions sont strictement positives on compare le quotient \( \frac{f}{g} \) à 1.
Ici f et g sont strictement positives : \( \frac{f(x)}{g(x)}=\frac{e^{-x}}{e^{-2x}}=e^{-x+2x} = e^x \)
Donc sur Cf est en dessous de Cg et sur
Cf est au dessus de Cg

On résout l'équation \( e^{-5x^2} \leq 1: \)
Or pour tout réel x on a \( -5x^2 \leq 0\) donc la courbe C reste en dessous de la droite avec un point de contact : J (0 ; 1)
Équation de la tangente à la courbe au point J ?
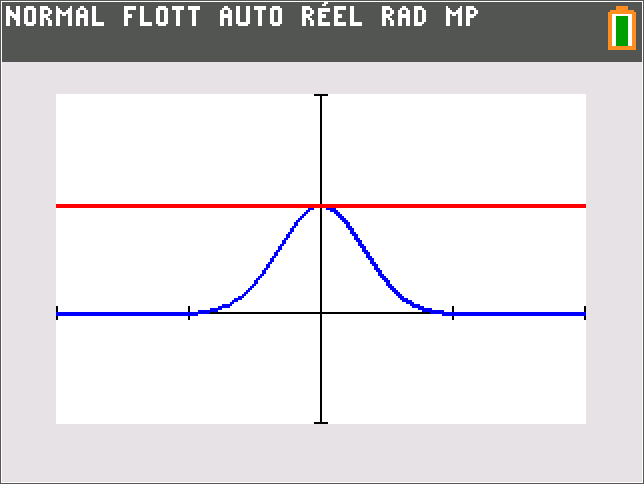

Pour étudier les positions relatives des courbes Cf et Cg, on peut procéder comme dans l'exercice 21. Ici on va étudier le signe de \( f - g \) :
Comme pour tout nombre réel x, \(e^{-x^2}>0, \)
\( f(x)-g(x)\geq 0\Leftrightarrow 1-e^{-x^2}\geq 0\)
Or pour tout réel x on a \( x^2 \geq 0\) donc la courbe Cf reste au dessus de la courbe Cg avec un point de contact : J (0 ; 1)


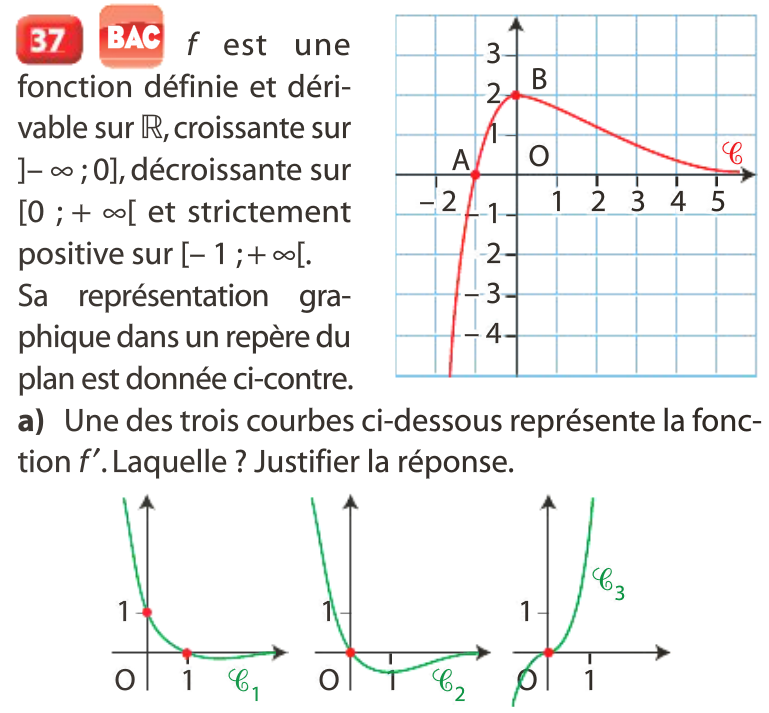
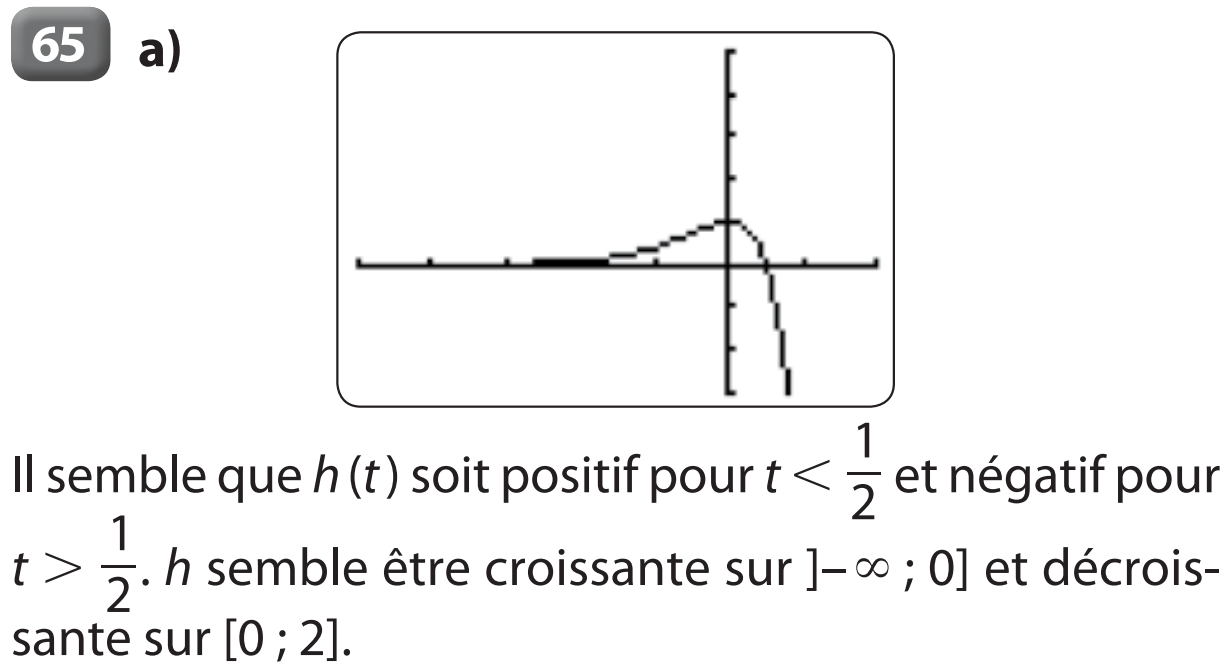
a) f est croissante sur ]–∞ ; 0] et décroissante sur [0 ; +∞[, donc f ’ est positive sur ]–∞ ; 0] et négative sur [0 ; +∞[, ce qui correspond à la courbe C2.
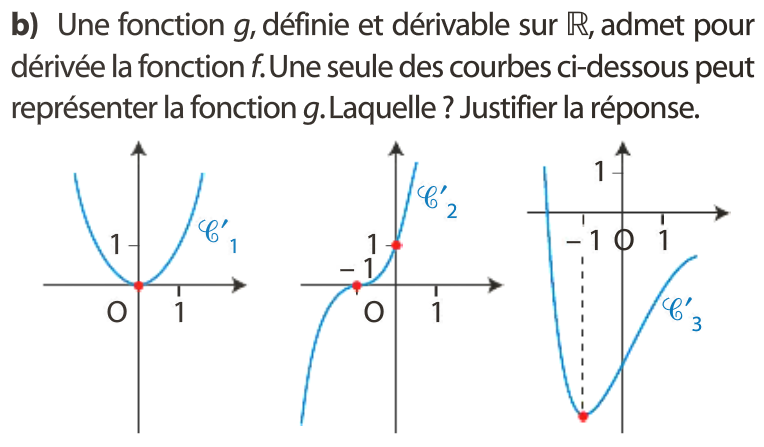
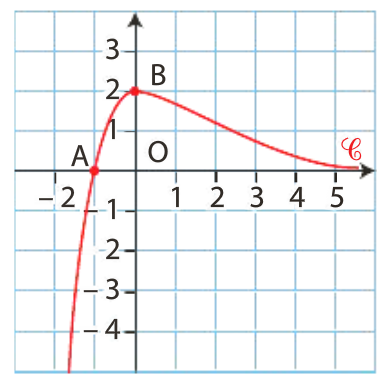
f est négative sur ]–∞ ; –1] et positive sur ]–1 ; +∞[. Donc si f = g’ alors g est décroissante sur ]–∞ ; – 1] et croissante sur ]–1 ; +∞[. Seule la courbe C’3 peut représenter g.


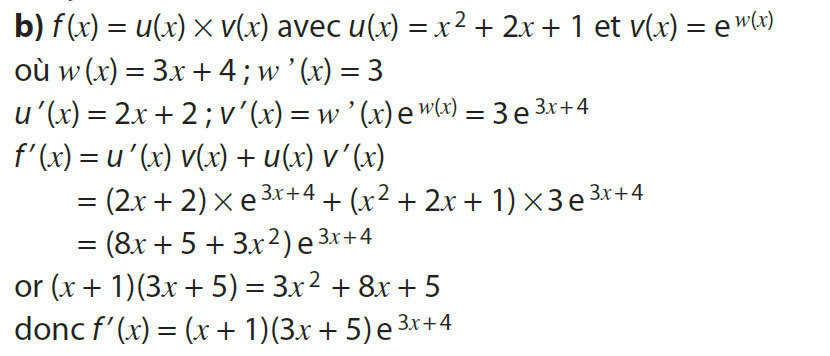
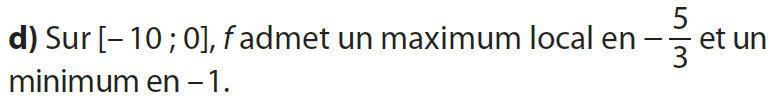

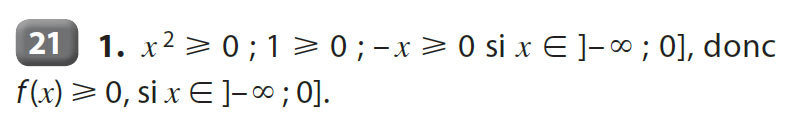



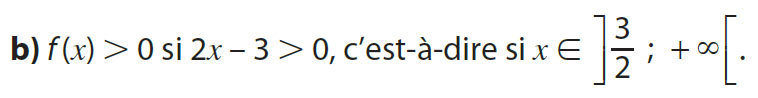
Terminale ES : Fonctions exponentielles
By Jean-Marc Kraëber
Terminale ES : Fonctions exponentielles
Lycée Saint-Exupery - La Rochelle
- 2,018



