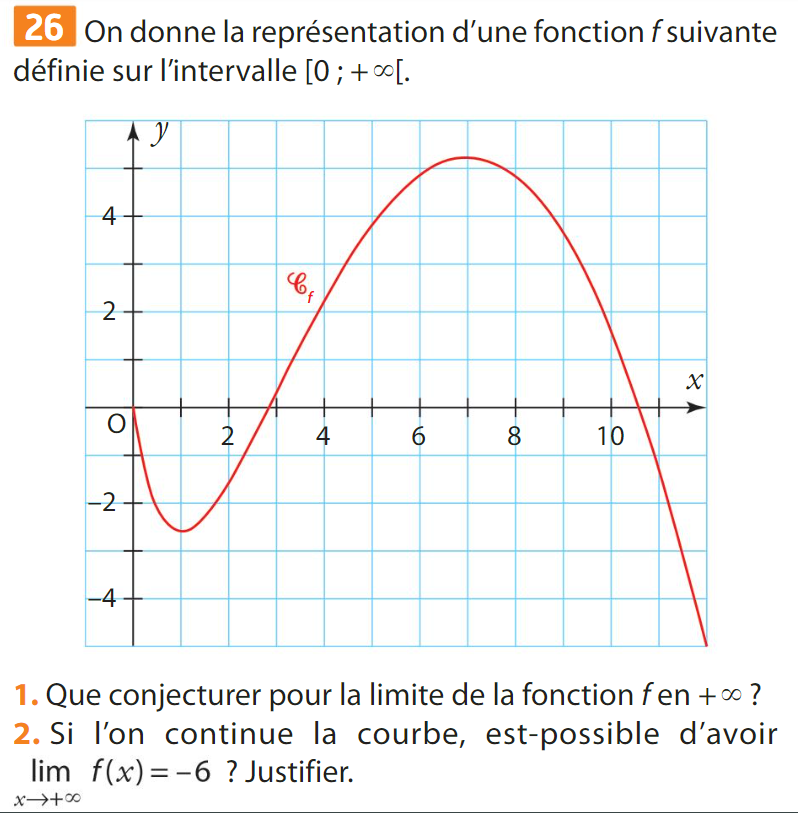
Limites et continuité



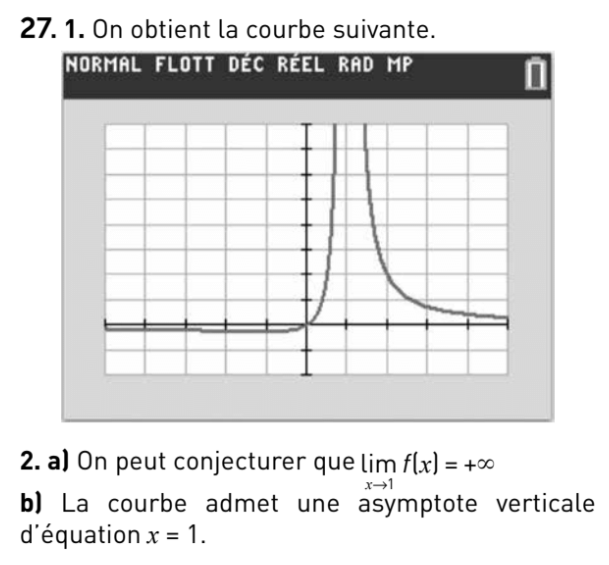



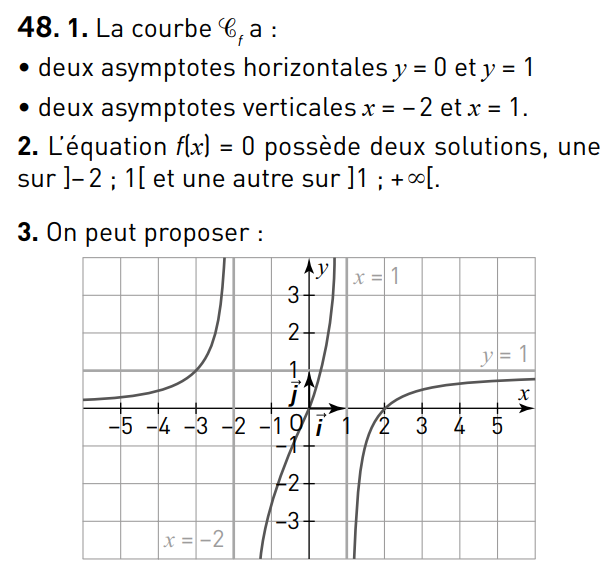
la droite d'équation \(y=0\) et la droite d'équation \(y=1\).




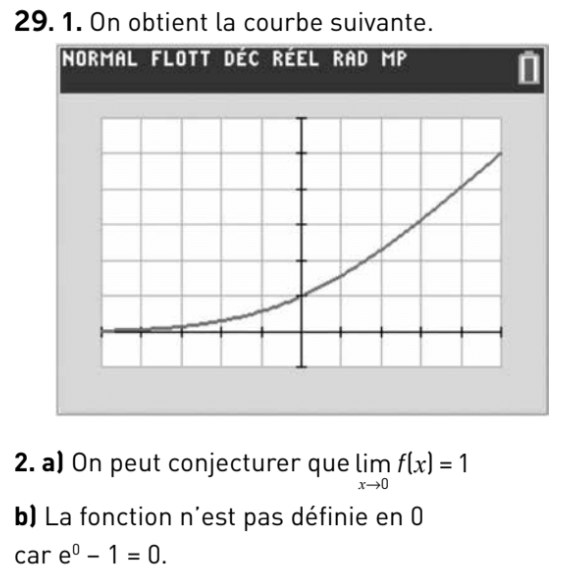







32 p 58
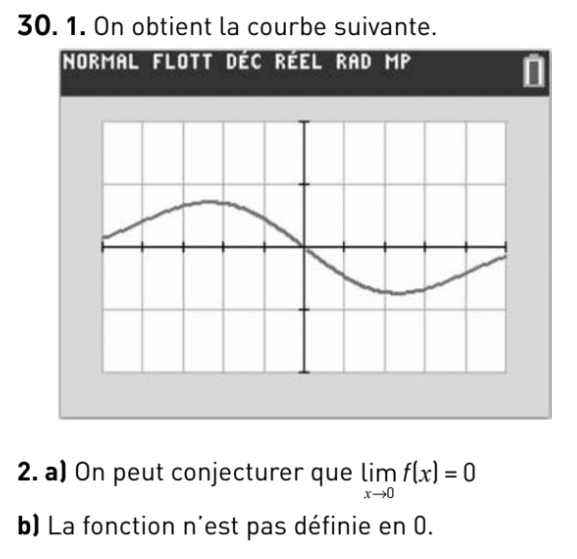
33 p 58
donc les limites à droite et à
gauche du quotient sont infinies.
Pour déterminer s'il s'agit de \(+\infty\) ou de \(-\infty\), on étudie le signe de \(e^x-1\) selon les valeurs de \(x\).
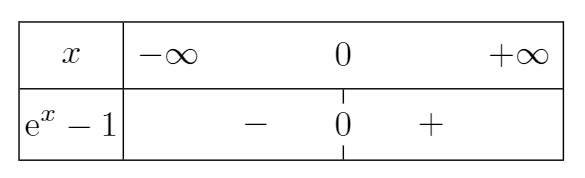
On obtient le tableau de signes suivant :
34 p 58
donc les limites à droite et à gauche du quotient sont infinies.
Pour déterminer s'il s'agit de \(+\infty\) ou de \(-\infty\), on étudie le signe de \(x+1\) selon les valeurs de \(x\).
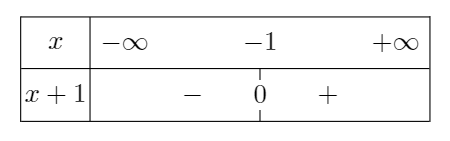

35 p 58
donc les limites à droite et à gauche du quotient sont infinies.
Pour déterminer s'il s'agit de \(+\infty\) ou de \(-\infty\), on étudie le signe de \(1-e^x\) selon les valeurs de \(x\).
On obtient le tableau de signes suivant :
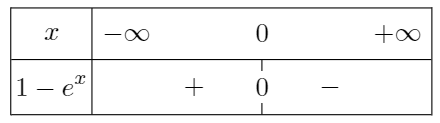
36 p 58
donc les limites à droite et à gauche du quotient sont infinies.
Pour déterminer s'il s'agit de \(+\infty\) ou de \(-\infty\), on étudie le signe de \(-x-1\) selon les valeurs de \(x\).
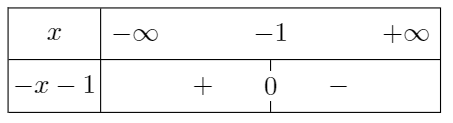

38 p 59
donc on obtient une forme indéterminée \(\ \dfrac{\infty}{\infty} \).
donc on obtient une forme indéterminée \(\ \dfrac{\infty}{\infty} \).
39 p 59
40 p 59
Donc on obtient une forme indéterminée \(\ \dfrac{\infty}{\infty} \).
Donc on obtient une forme indéterminée \(\ \dfrac{\infty}{\infty} \).
Donc on obtient une forme indéterminée \(\ \dfrac{\infty}{\infty} \).
Donc on obtient une forme indéterminée \( +\infty\;-\infty \).
Donc on obtient une forme indéterminée \(\ \dfrac{\infty}{\infty} \).
Donc on obtient une forme indéterminée \( +\infty\;-\infty \).
Donc on obtient une forme indéterminée \(\ \dfrac{\infty}{\infty} \).
Dérivation : Automatismes
Dérivation : Automatismes
Dérivation : Automatismes
Dérivation : Automatismes
Dérivation : Automatismes

Pour étudier les variations d'une fonction il faut généralement étudier le signe de sa dérivée.
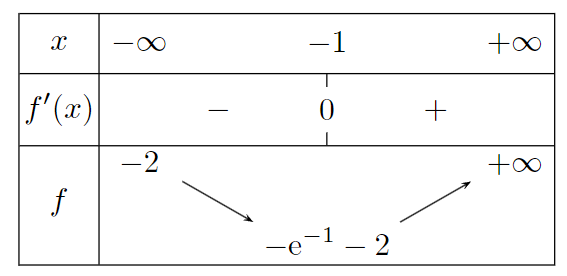


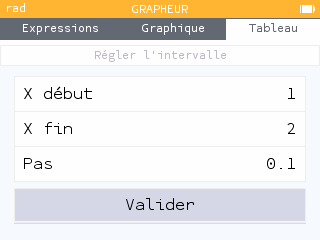
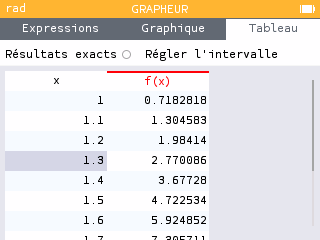
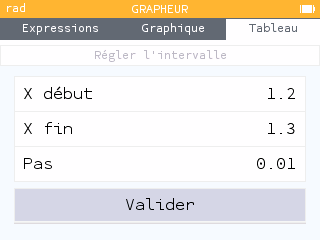
Méthode par balayage


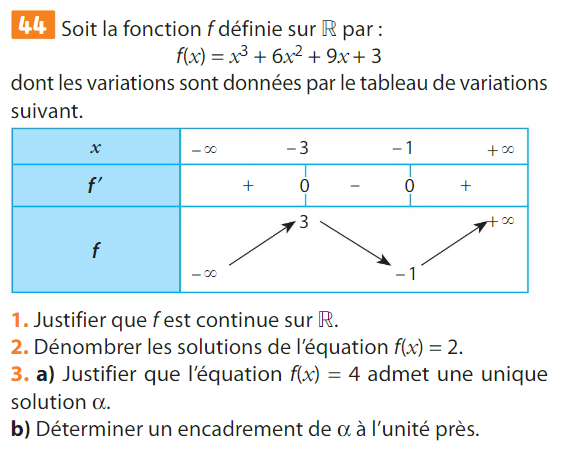




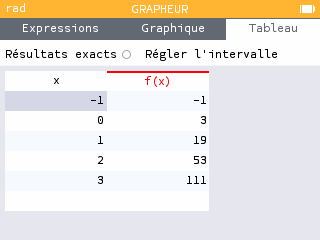
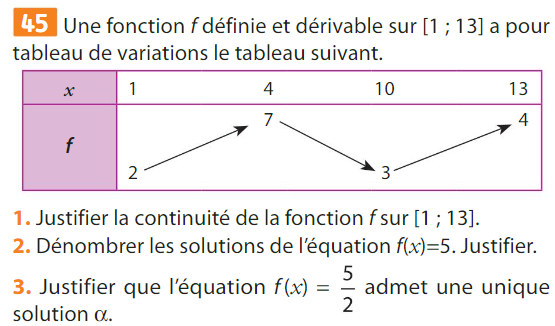


La fonction \(f\) est dérivable sur \([1~;~13]\) donc elle est continue sur cet intervalle.
















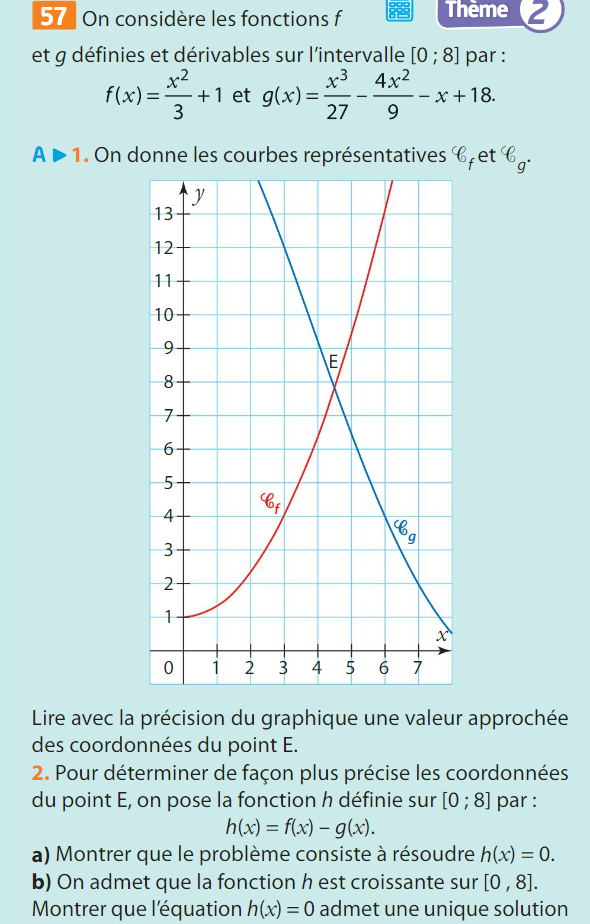


strictement croissante


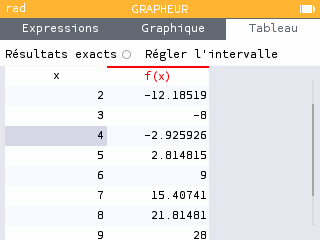
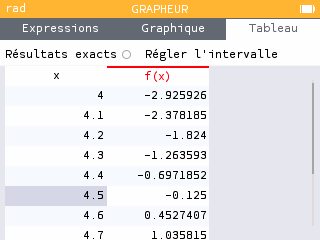
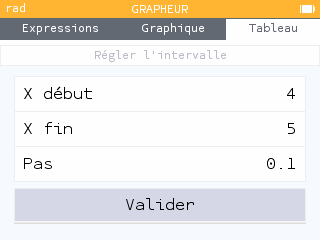
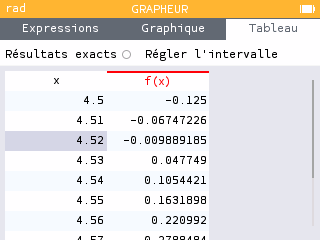
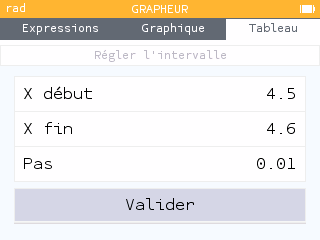
Méthode 2 :

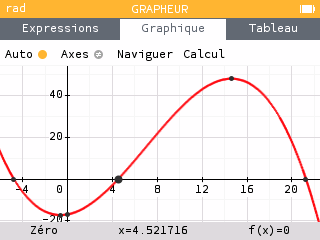

1. Le prix unitaire d'équilibre est de 452 €.

2. Le nombre d’articles correspondant est de 7 800.
1. Le prix unitaire d'équilibre est de 452 €.


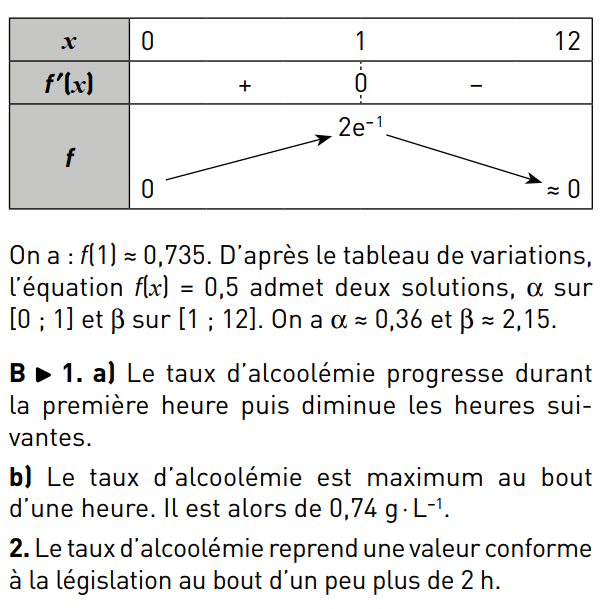






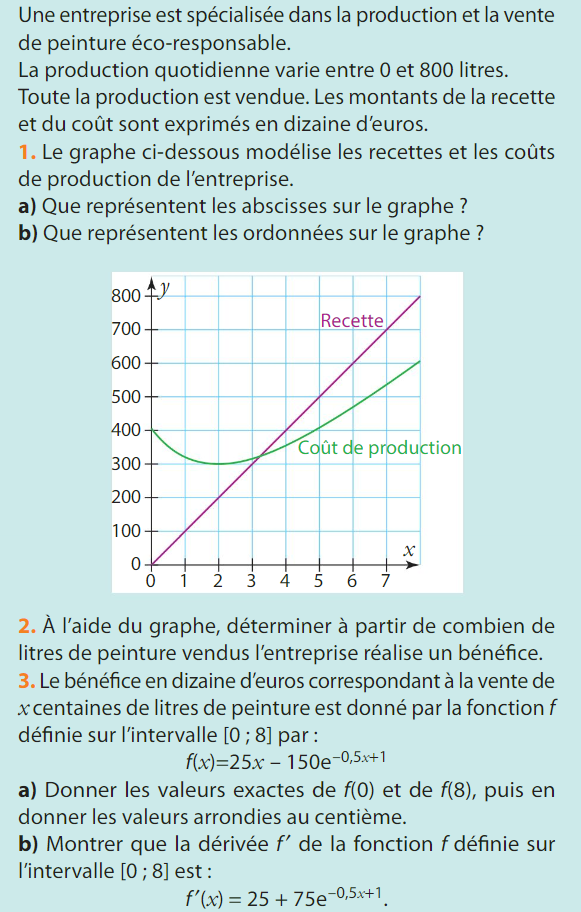
64 p 63











Limites et continuité
By Jean-Marc Kraëber
Limites et continuité
Lycée Saint-Exupery La Rochelle
- 2,159



