Loi normale
N(\mu\,;\sigma^2)
Une variable aléatoire X suit la loi normale \(N(\mu\,;\sigma^2)\)
si la variable aléatoire \(\dfrac{X-\mu}\sigma\) suit la loi normale centrée réduite.
Sa densité est la fonction \(f\) définie sur \(\mathbb{R}\) par
f(x)=\frac{1}{\sigma\sqrt{2\pi}}\text{e}^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}
Courbe symétrique
par rapport à la
droite d'équation \(x = \mu\).
Si la variable aléatoire X suit la loi normale \(N(\mu\,;\sigma^2)\)
alors son espérance est \(\mu\) et son écart-type est \(\sigma\).
Pour un même écart-type \(\sigma\) (0,5 sur la figure ci-dessous), lorsque \(\mu\) varie, la courbe garde la même forme mais se "déplace" sur l’axe des abscisses.
Pour une même espérance \(\mu\), lorsque l’écart type \(\sigma\) varie, la forme de la courbe évolue : plus \(\sigma\) est grand plus la courbe est évasée et le maximum de la fonction petit.
En effet, un écart-type important signifie que la dispersion des données est importante.
Utilisation de la calculatrice
TI : 2nde var (distrib)
CASIO : menu Stat. - DIST(F5) - NORM(F1) - Ncd(F2)
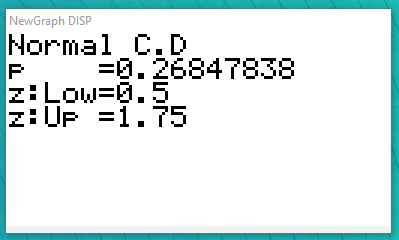
Déterminer à l'aide de la calculatrice le nombre \(u\) tel que
p(X\leqslant u) =p_0\;
Exemple :
avec connue.
p_0
Méthode : Quand on connait pas \(\mu\), il faut faire un changement de variable et utiliser la loi normale centrée réduite.
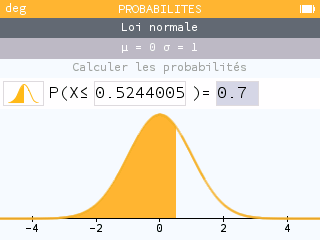
TI
Sur les anciens modèles, FracNormale au lieu de invNormale
CASIO : menu Stat. - DIST(F5) - NORM(F1) - InvN(F3)
\text{Donc } \dfrac{60-\mu}{20}\approx0,52
\Leftrightarrow 60-\mu\approx0,52 \times20
\Leftrightarrow -\mu\approx 10,4-60
\Leftrightarrow \mu\approx 49,6
Probabilités d’événements particuliers
Soit X une variable aléatoire suivant la loi normale \(N(\mu\,;\sigma^2)\)
p(\mu-\sigma\leqslant X \leqslant \mu+\sigma)\approx0,68
p(\mu-2\sigma\leqslant X \leqslant \mu+2\sigma)\approx0,95
p(\mu-3\sigma\leqslant X \leqslant \mu+3\sigma)\approx0,997
\text{Rappel : } p(X< t) = 1-p(X> t)
p(X<500)=p\left(Z<\dfrac{500-\mu}{20}\right)=0,1
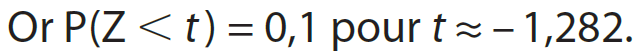
Rappel : Quand on connait pas \(\mu\), il faut faire un changement de variable et utiliser la loi normale centrée réduite.
On note X la variable aléatoire qui donne la masse d'un paquet de riz.
On note X la variable aléatoire qui donne le volume de jus versé.
La boisson déborde du gobelet si le volume de jus versé est supérieur à la contenance du gobelet.
p(Z< t)=1-p(Z>t)= 1-0,001=0,999
Penser aux probabilités d’événements particuliers...
p(\mu-\sigma\leqslant X \leqslant \mu+\sigma)\approx0,68
On sait que si une variable aléatoire X suit la loi normale \(N(\mu\,;\sigma^2)\) alors
Donc la probabilité que la note d'un élève pris au hasard soit comprise entre 7,4 et 11 est d'environ 0,68
p(\mu-2\sigma\leqslant X \leqslant \mu+2\sigma)\approx0,95
p(\mu-3\sigma\leqslant X \leqslant \mu+3\sigma)\approx0,997
On sait que si une variable aléatoire X suit la loi normale \(N(\mu\,;\sigma^2)\) alors
Donc la probabilité que la note d'un élève pris au hasard soit comprise entre 5,6 et 12,8 est d'environ 0,95
On sait que si une variable aléatoire X suit la loi normale \(N(\mu\,;\sigma^2)\) alors
Donc la probabilité que la note d'un élève pris au hasard soit comprise entre 3,8 et 14,6 est d'environ 0,997
On note X la variable aléatoire qui donne la taille d'une candidate.
p(\mu-2\sigma\leqslant X \leqslant \mu+2\sigma)\approx0,95
On sait que si X suit la loi normale \(N(\mu\,;\sigma^2)\) alors
\text{On peut donc poser}\left\{\begin{array}{rcl} \mu-2\sigma&=&169,6 \\ \mu+2\sigma&=&180,4\end{array}\right.
On ajoute membre à membre les deux équations et on obtient :
2\mu = 350\Leftrightarrow\mu=175
175+2\sigma = 180,4\Leftrightarrow \sigma = 2,7
X suit la loi normale \(N(175\,;2,7^2)\).
p(\mu-\sigma\leqslant X \leqslant \mu+\sigma)\approx0,68
On sait que si une variable aléatoire X suit la loi normale \(N(\mu\,;\sigma^2)\) alors
\text{Donc ici }p(172,3\leqslant X \leqslant 177,7)\approx0,68
1-0,68=0,32 \text{ donc environ 32\% des candidates}
\text{seraient refusées.}
p(\mu-3\sigma\leqslant X \leqslant \mu+3\sigma)\approx0,997
On sait que si une variable aléatoire X suit la loi normale \(N(\mu\,;\sigma^2)\) alors
Loi normale
By Jean-Marc Kraëber
Loi normale
Lycée Saint-Exupery
