Suites Numériques
1 Rappels sur les suites arithmétiques :
La relation de récurrence
Soit (un) une suite arithmétique de raison r et de premier terme u0.
La formule explicite
permet de calculer les termes de "proche en proche".
permet de calculer un terme de rang quelconque.
Quand on ne connait pas u0 :
2 Rappels sur les suites géométriques :
Soit (un) une suite géométrique de raison q.
La relation de récurrence
La formule explicite
permet de calculer les termes de "proche en proche".
permet de calculer un terme de rang quelconque.
Quand on ne connait pas u0 :
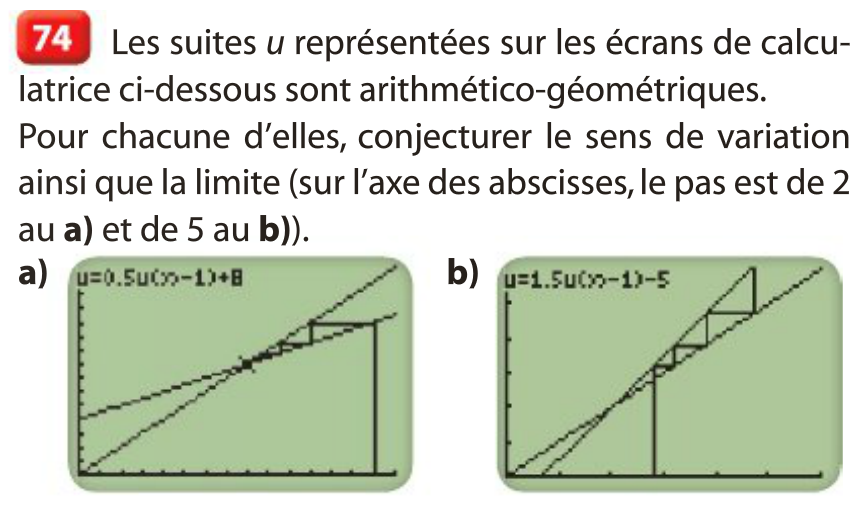
3 Sens de variation et représentation graphique d'une suite géométrique
Théorème : Soit (un) une suite géométrique de raison q et de premier terme u0 positif.
- Si q > 1, alors la suite (un) est croissante.
- Si 0 < q < 1, alors la suite (un) est décroissante.
- Si q < 0, la suite (un) n’est pas monotone.
Démonstration :
Méthode : Pour donner le sens de variation d'une suite on peut étudier le signe de un+1 - un


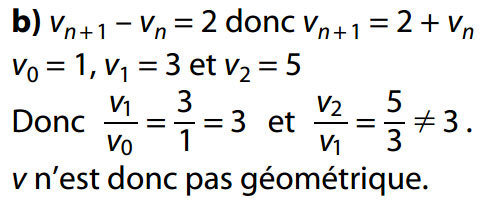
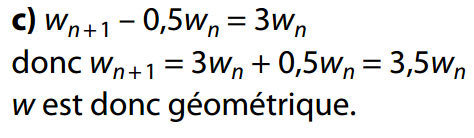
- Pour montrer qu'une suite (un) est géométrique de raison q, on montre que pour tout n la suite (un) vérifie un+1 = q un
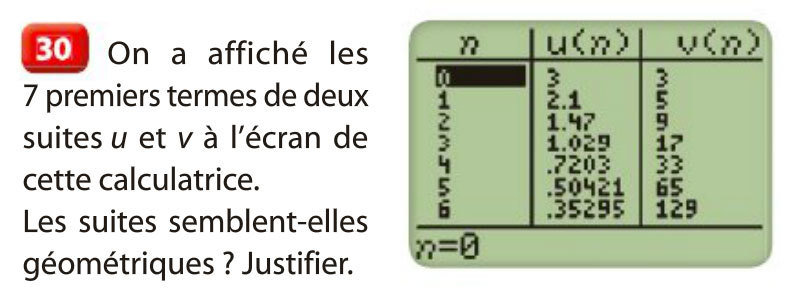
- Pour montrer qu'une suite n'est pas géométrique, un contre exemple suffit :
par exemple

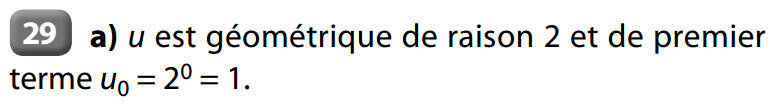
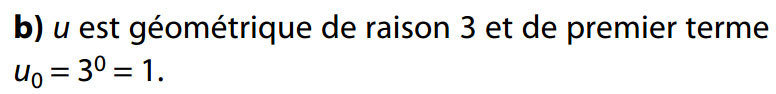
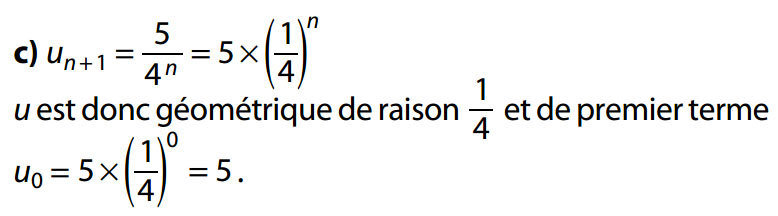
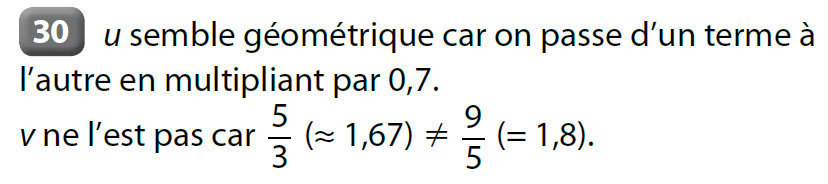



terme de rang n

b) Cet algorithme calcule le terme de rang n d’une suite arithmétique (un) de raison 2 et de premier terme u0 = 5.

Si q > 0, on a :
est strictement décroissante.
Si q < 0,
donc (un) n'est pas monotone.
- Si q = 1, (un) est constante.
- Les résultats précédents sont inversés si u0 est négatif
- On dit que les suites géométriques ont une évolution exponentielle.
Remarques :
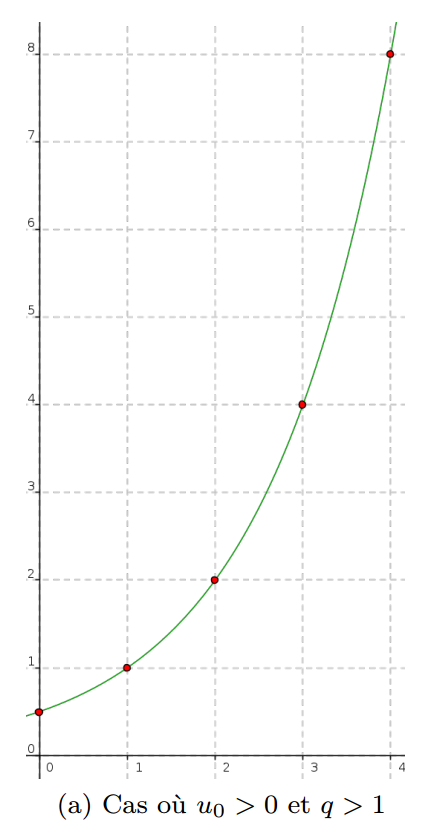
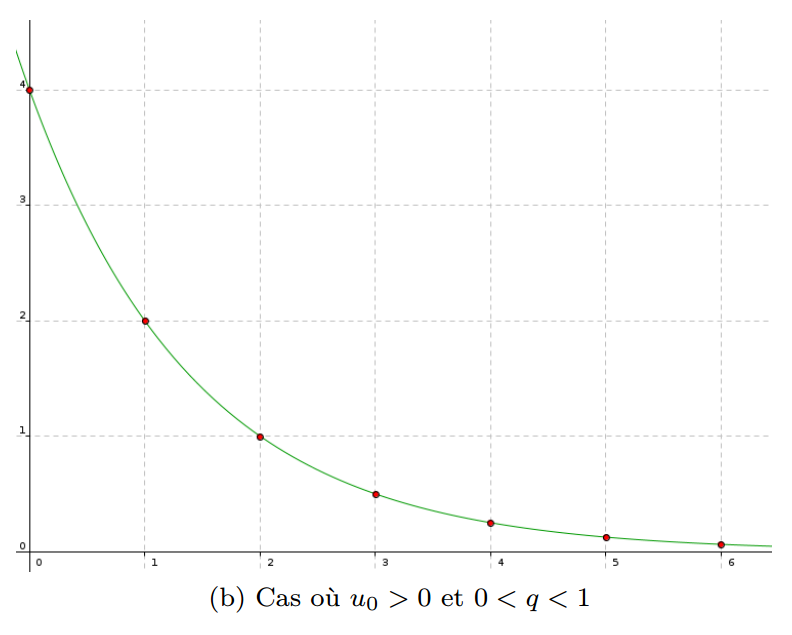
Représentation graphique :


Méthode : Pour montrer qu'une suite est géométrique, on peut écrire sa formule explicite sous la forme

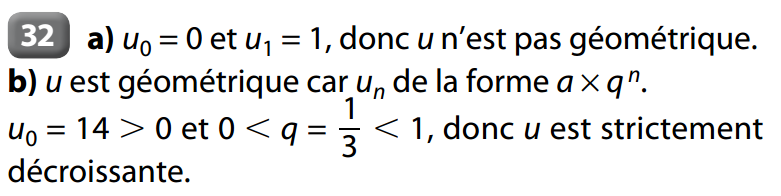
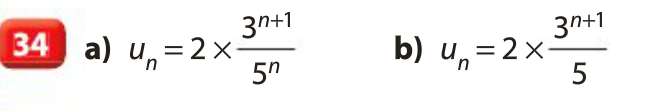
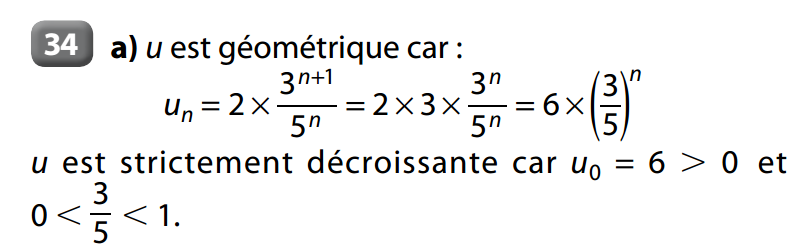
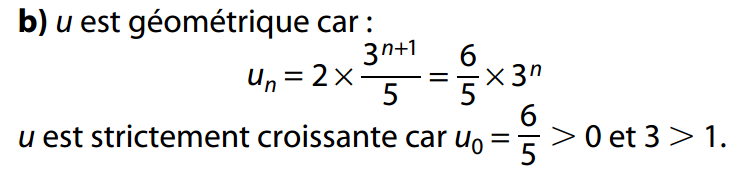
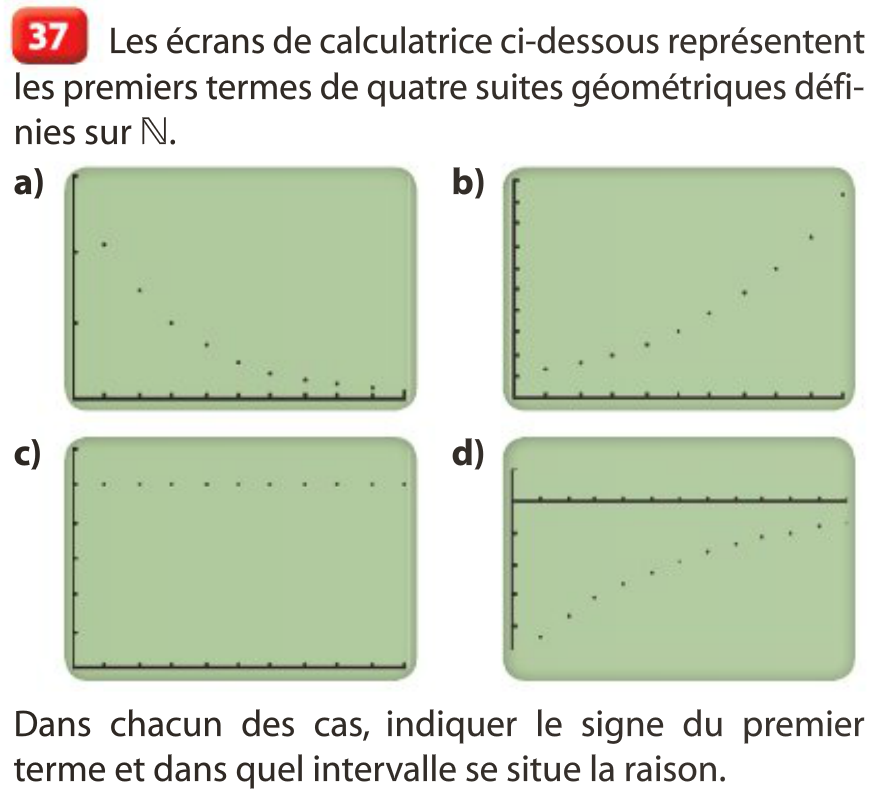







4 Somme de termes d’une suite géométrique :
Théorème : Soit (un) une suite géométrique de raison q (avec ). On note Sn la somme des (n + 1) premiers termes de la suite (un), c’est-à-dire :
Alors on a :
Démonstration :
En effet si on note, on a :
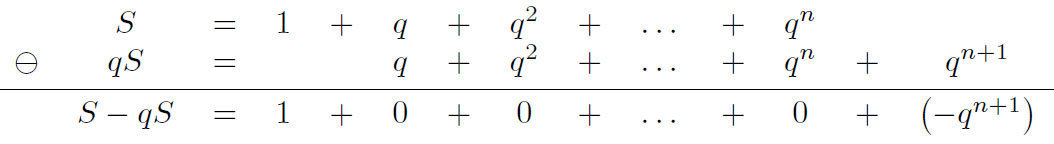
On a donc :
et comme
D'où :
De plus :
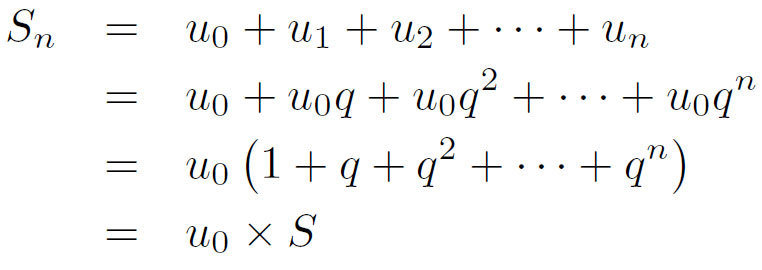
On a bien :
n+1 est le nombre de termes !
Remarque : si q = 1 alors on a :
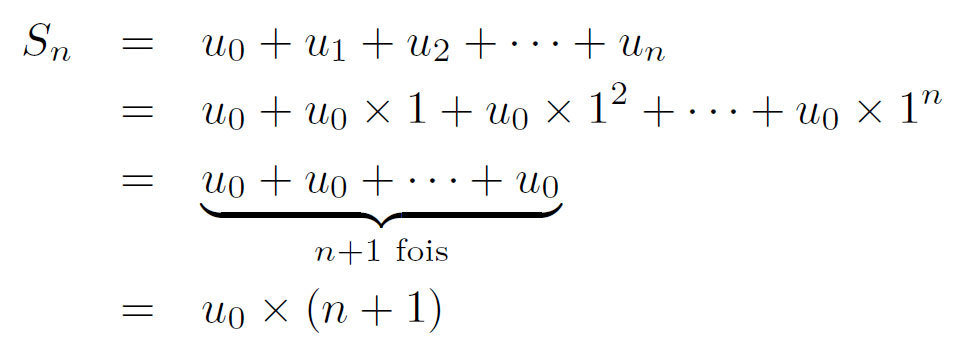
Exemple :
Calculer la somme des 10 premiers termes de la suite géométrique de premier terme u0 = 100 et de raison
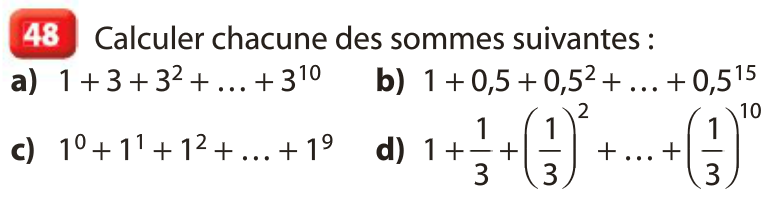
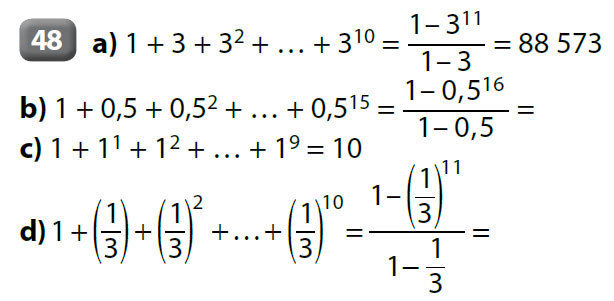

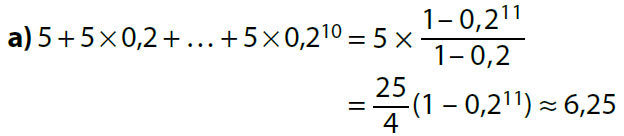
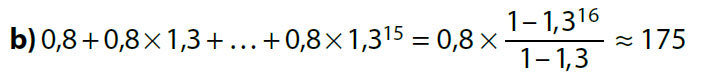
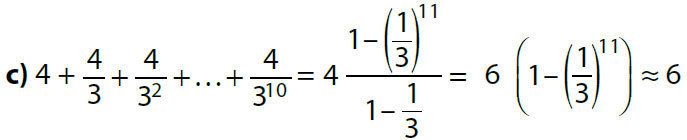
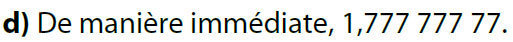
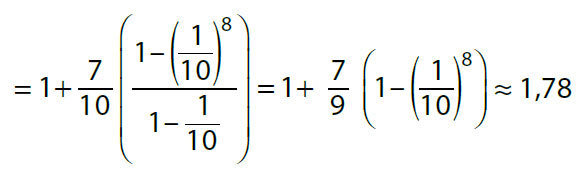


5 Limite d'une suite géométrique
5.1 Notion de limite
Étudier la limite d’une suite un, c’est déterminer ce que devient un lorsque n devient très grand (on dit que n
tend vers +∞).
Exemples :



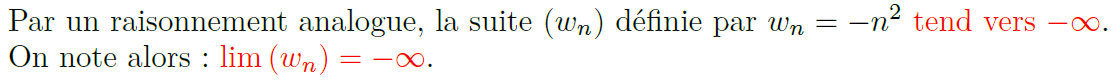
Remarque :
Attention, le terme « converge » n’est utilisable que pour des suites de limite finie, pas pour des suites tendant vers −∞ ou +∞.
5.2 Quelques propriétés sur les limites

En particulier, si la suite (un) converge vers zéro, la suite (aun + b) converge vers b.
Remarque :


Lorsque (un) tend vers l’infini, les suites (un) et (un + b) ont la même limite.
Remarque :
5.3 Limite d'une suite géométrique

Exemples :
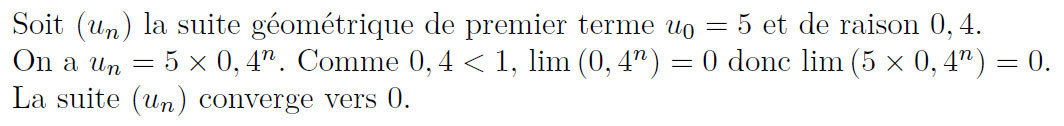

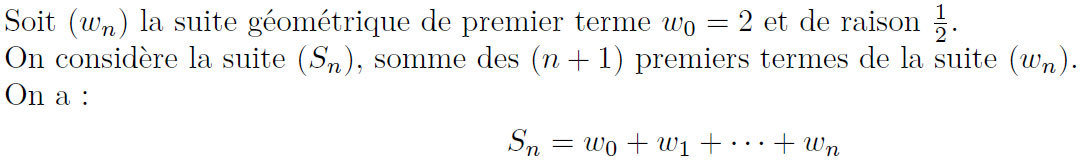
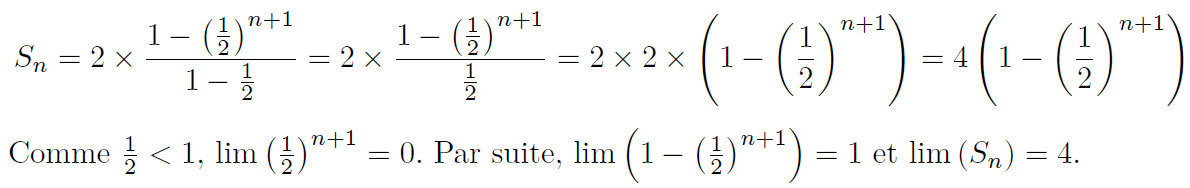
6 Suites arithmético-géométrique
Définition : On appelle suite arithmético-géométrique toute suite (un) vérifiant une relation de récurrence de la forme : où a et b sont deux réels.
Remarque : En particulier,
- Si a = 1 , (un) est une suite arithmétique de raison b ;
- si b = 0, (un) est une suite géométrique de raison a.
6.1 Définition

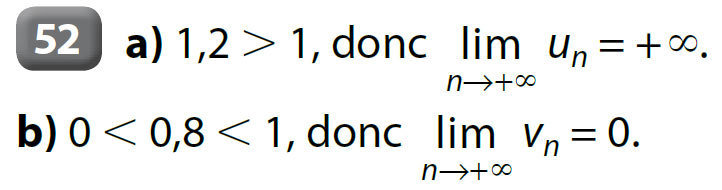
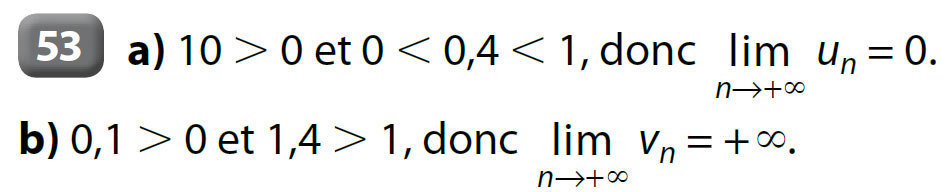
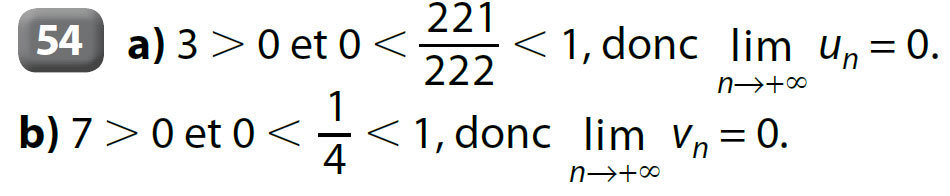
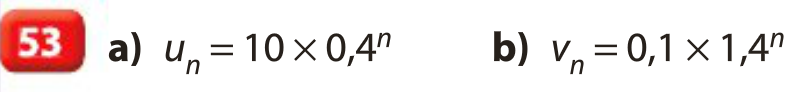
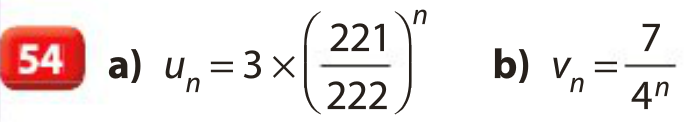

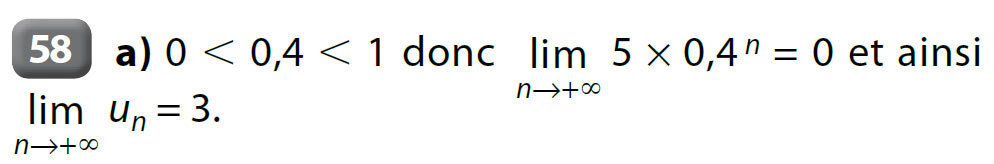
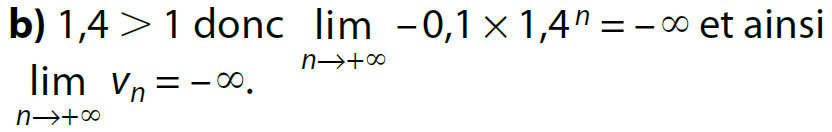
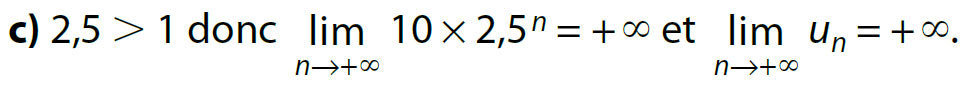
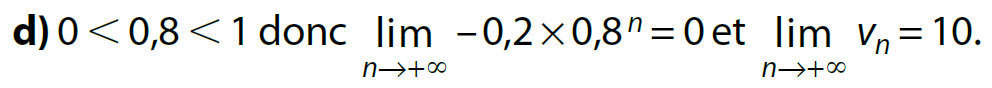
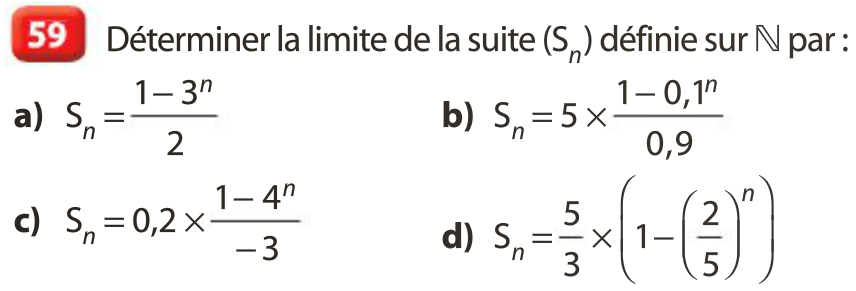
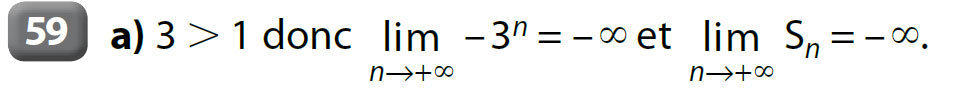
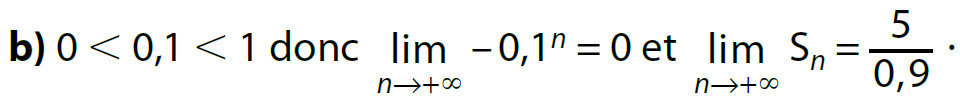
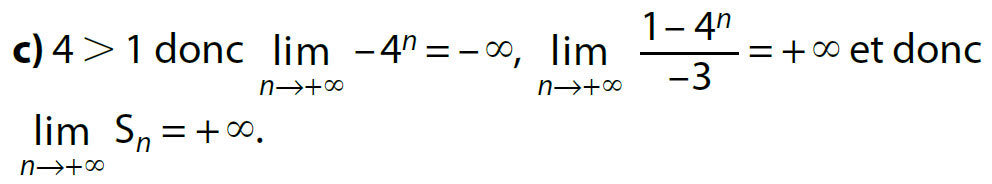
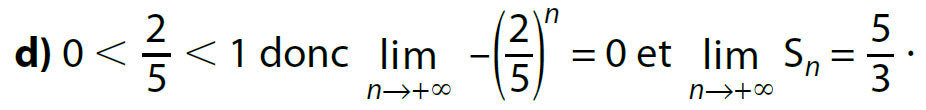
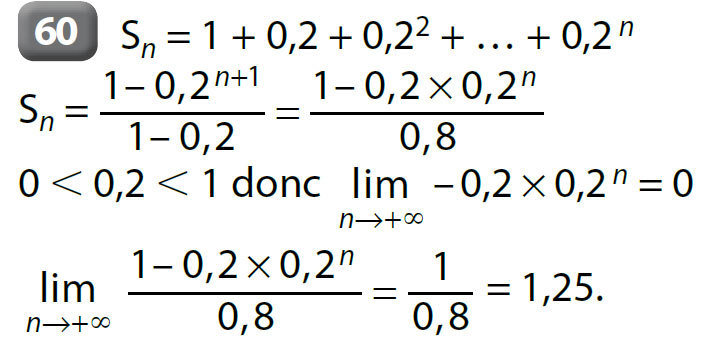
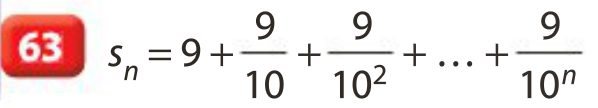
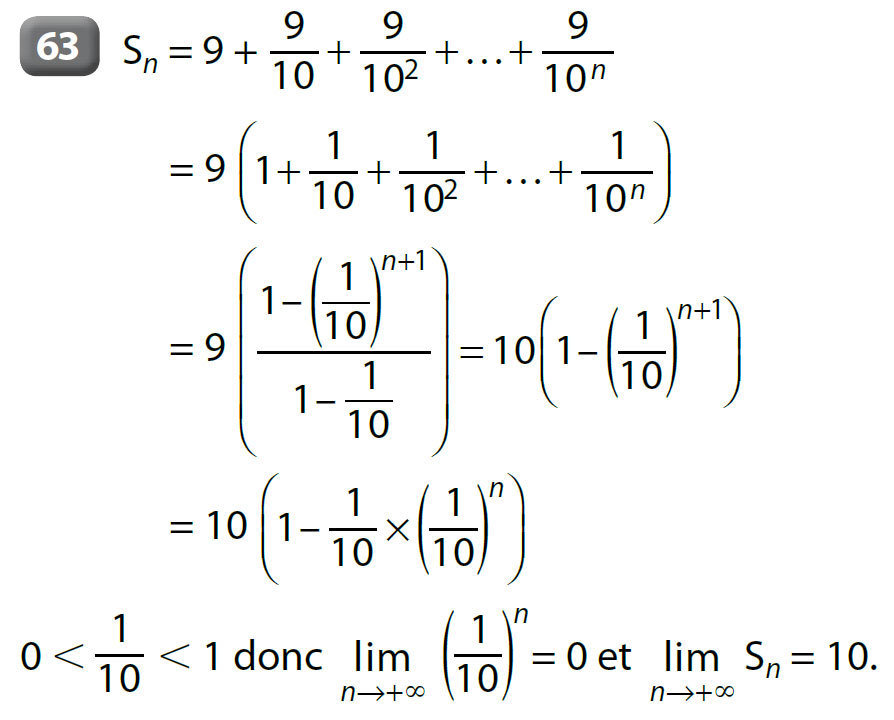
6.2 Exemple d’utilisation d’une suite intermédiaire
Une société de crédit propose à ses clients de mettre à leur disposition une somme de 6000 € remboursable par des prélèvements mensuels fixes de 300 €. Le taux d’intérêt mensuel annoncé est 1,5%. On se propose de déterminer le nombre de mois nécessaires au remboursement de cette somme. On pose u0 = 6000, et on appelle un le montant restant à rembourser après n prélèvements.
- Montrer que : Calculer u1 puis u2.
Au bout d’un mois, la somme à rembourser (u0 = 6000) a été augmentée de 1,5 %, soit multipliée par 1,015. Il faut soustraire à cette somme le montant de la première mensualité (300 €). On a donc :
Par un raisonnement analogue, au bout de 2 mois, la somme à rembourser précédente (u1 = 5790) a été augmentée de 1,5 %, soit multipliée par 1,015. Il faut soustraire à cette somme le montant de la deuxième mensualité (300 €). On a donc :
2. Montrer de manière générale que pour tout entier naturel n,
Plus généralement, chaque mois, le montant restant à rembourser du mois précédent est augmenté de 1,5 %, et on lui déduit la mensualité en cours. On a donc :
3. On considère la suite (vn) définie pour tout entier n par
a) Montrer que (vn) est une suite géométrique.
Pour tout entier naturel n,
La suite (v n) est donc bien une suite géométrique de raison
q = 1,015.
Son premier terme est v 0 = −14000.
b. Exprimer alors vn puis un en fonction de n.
De plus, comme vn = un − 20 000, on a :
4. Combien de mois sont-ils nécessaires au remboursement du crédit ?
Le crédit est remboursé dès que un devient négatif ou nul.
Méthode 1 : Tableau de valeurs sur la calculatrice en mode suite :
On remarque que u23 > 0 et u24 < 0. Le crédit sera donc remboursé en 24 mois.

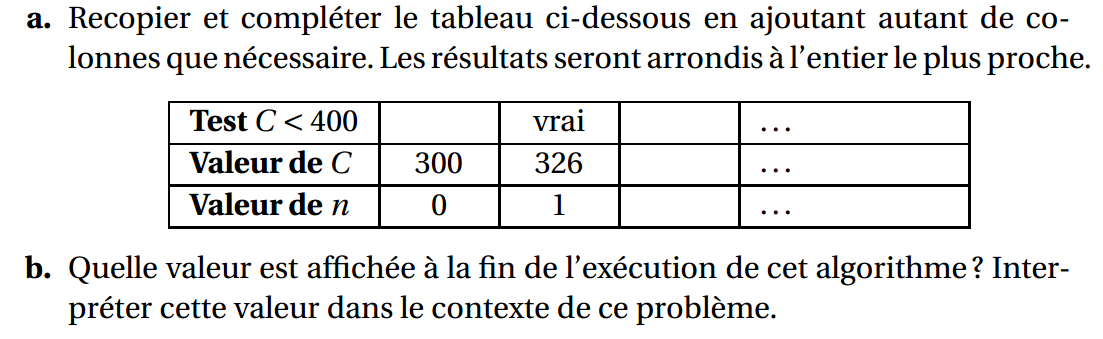
Méthode 2 : Programmer un algorithme de seuil sur la calculatrice :
Sur TI : prog/nouveau/entrer
Entrée : (pas de saisie)
Traitement :
Initialisation : U prend la valeur 6000 (valeur de u0)
N prend la valeur 0 (valeur de n)

Algorithme en langage naturel + TI + Casio
Boucle "Tant que" :
Tant qu'une condition est réalisée, une ou plusieurs instructions sont exécutées. Lorsque la condition n'est plus réalisée, la boucle s'arrête.
Tant que U > 0
U prend la valeur 1,015U − 300
(un+1 = 1,015un − 300)
N prend la valeur N + 1
Fin Tant que

Sortie : Afficher n (affiche le nombre de mois nécessaire au remboursement total du crédit).
L'algorithme va calculer de proche en proche les termes de la suite (u1, u2, u3...) tant qu'ils sont strictement positifs. Dès qu'un terme est inférieur ou égal à 0, la boucle s'arrête.
TI :

CASIO:
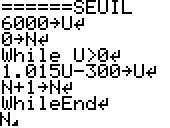
Exécution de l'algorithme : quitter/prgm/EXéC.


Le crédit sera donc remboursé en 24 mois.

a) Chaque année, le nombre d’habitants augmente de 5 %, donc est multiplié par 1,05, auquel il faut ajouter 4 000 personnes supplémentaires. a = 1,05 et b = 4 000.
b) En 2006, le nombre d’habitants est de :
u1 = 1,05 × 100 000 + 4 000 = 109 000.
En 2007, le nombre d’habitants est de :
u2 = 1,05 × 109 000 + 4 000 = 118 450.

a) u1 = 3 × u0 – 4 = 3 × 5 – 4 = 11
u2 = 3 × u1 – 4 = 3 × 11 – 4 = 29
u3 = 3 × u2 – 4 = 3 × 29 – 4 = 83
b) u1 = – 0,6 × u0 + 4 = – 0,6 × 10 + 4 = – 2
u2 = – 0,6 × u1 + 4 = – 0,6 × (– 2) + 4 = 5,2
u3 = – 0,6 × u2 + 4 = – 0,6 × 5,2 + 4 = 0,88
c) u1 = 0,4 × u0 + 7 = 0,4 × 5 + 7 = 9
u2 = 0,4 × u1 + 7 = 0,4 × 9 + 7 = 10,6
u3 = 0,4 × u2 + 7 = 0,4 × 10,6 + 7 = 11,24



1) u1 = 0,9 × 500 + 20 = 470
u2 = 0,9 × 470 + 20 = 443
2. un + 1 = 0,9un + 20, donc u est une suite arithmético-géométrique de premier terme u0 = 20.
3. a) vn + 1 = un + 1 – 200
= 0,9un + 20 – 200
= 0,9un – 180
= 0,9(un – 180/0,9)
= 0,9 (un – 200)
vn + 1 = 0,9 vn
b) v est une suite géométrique de raison 0,9 et de premier terme v0 = u0 – 200 = 500 – 200 = 300.
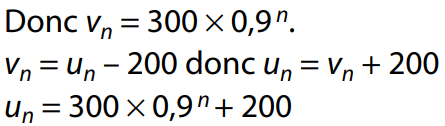
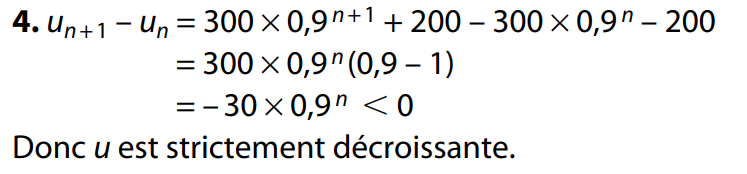
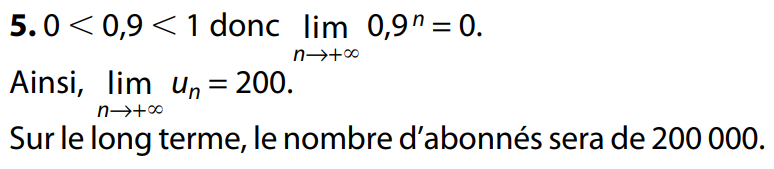

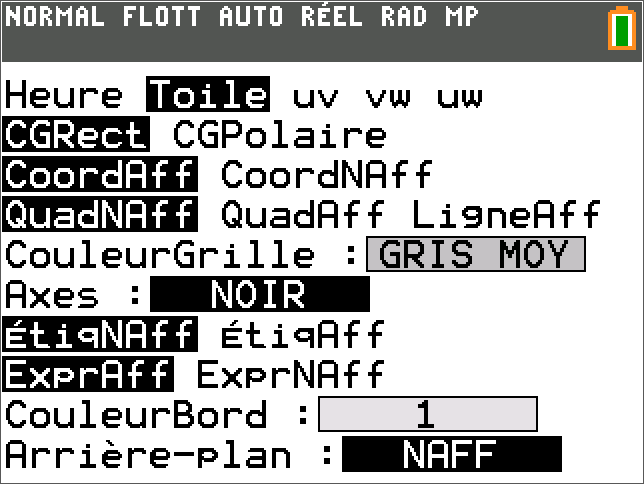
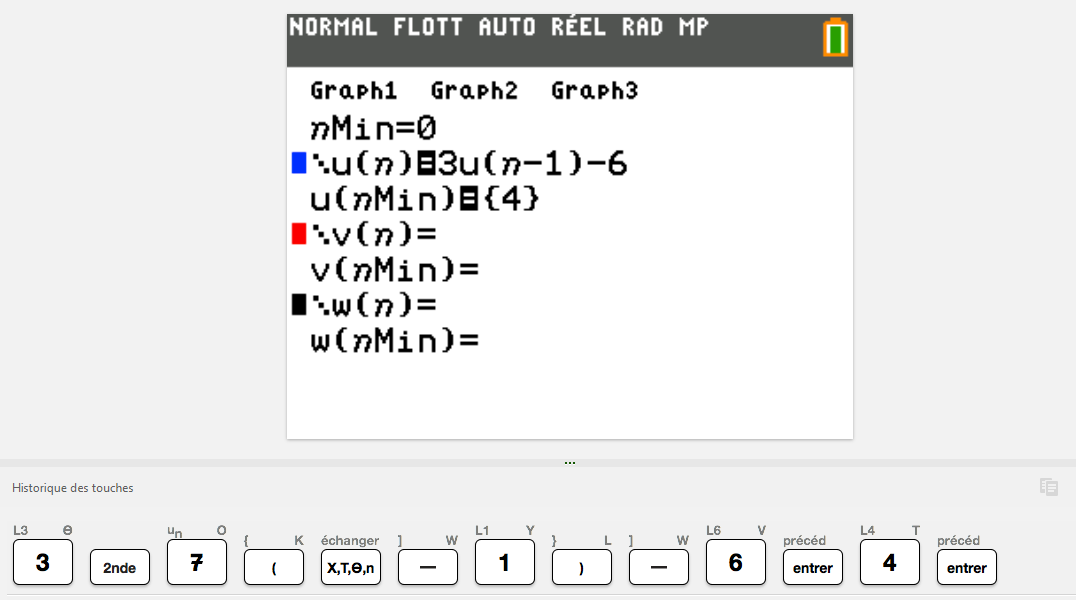
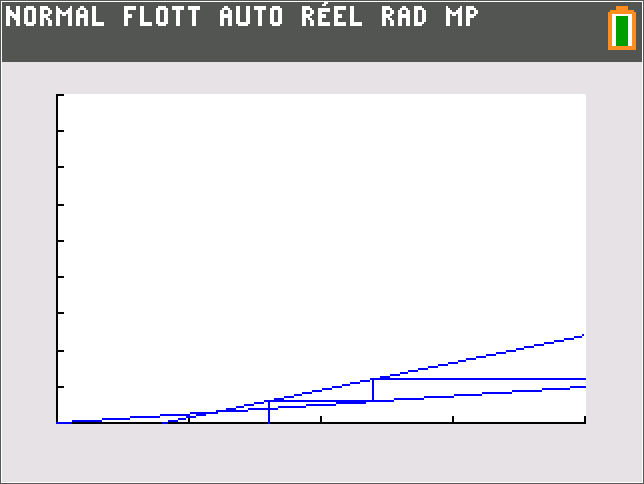
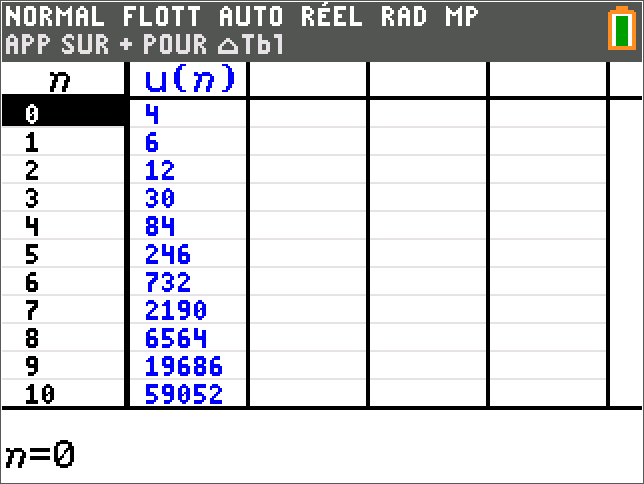
Représentation graphique d'une suite définie par récurrence
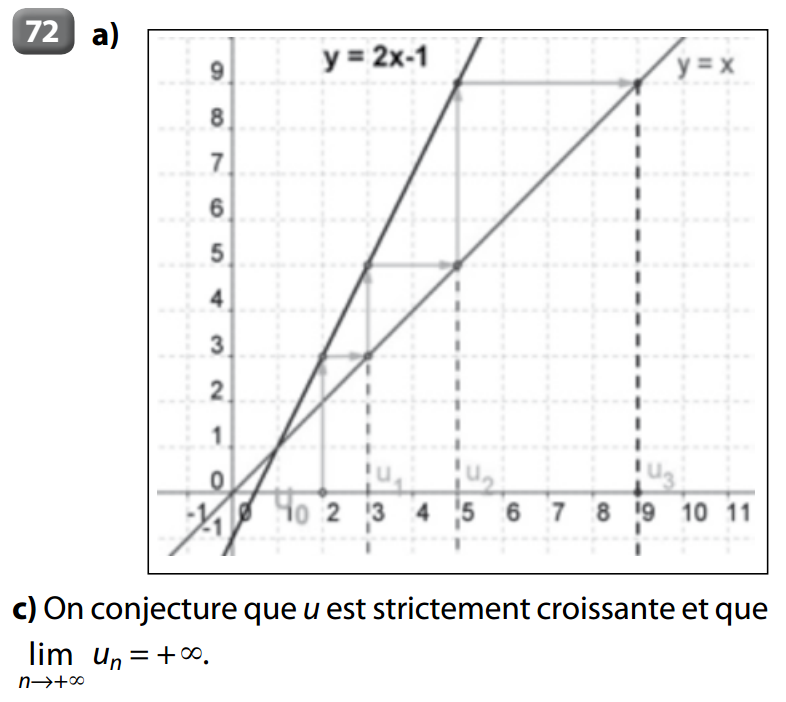

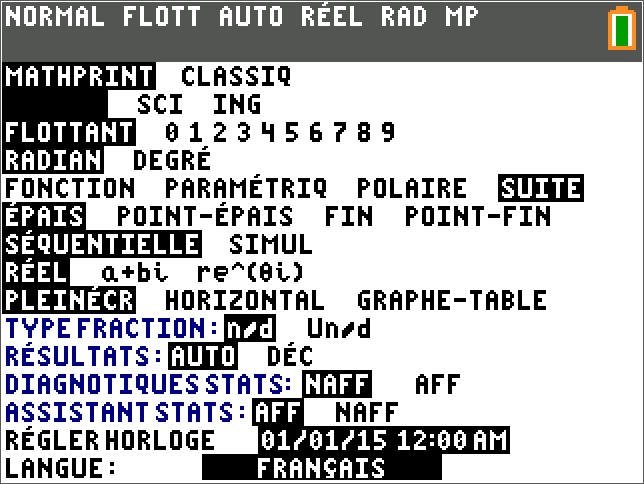
a) Sur TI 83 premium CE :
mode suite puis 2nde zoom(format)




Pondichéry 2015



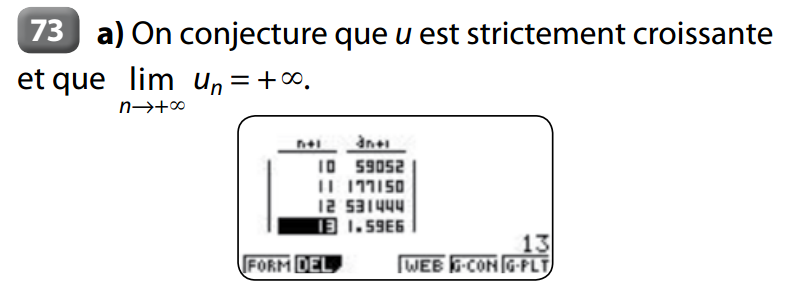
31

Amérique du nord 2015

4. Programmer l'algorithme


Term ES : Suites numériques
By Jean-Marc Kraëber
Term ES : Suites numériques
Lycée Saint-Exupery - La Rochelle
- 4,765



