Lois à densité
-
Lois à densité
-
Loi uniforme sur [a ; b]
-
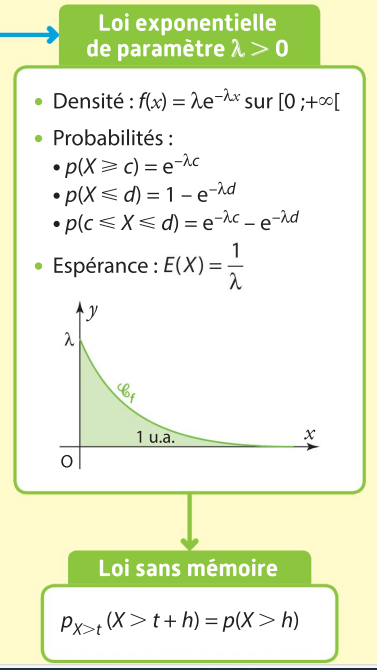
Loi exponentielle sur [0 ; +∞[
Lois à densité
En construction...
Rappels : l'équiprobabilité dans le cas d'un nombre fini d'issues
Ex. On lance un dé cubique bien équilibré dont les faces sont numérotées de 1 à 6.
Soit X, la variable aléatoire correspondant au numéro obtenu.
X est une variable aléatoire discrète : elle prend un nombre fini de valeurs : 1, 2, 3, 4, 5, 6.
Loi uniforme sur [a ; b]
La loi de probabilité associée est :
C'est une situation d'équiprobabilité : chacune des 6 issues a la même probabilité 61
La loi uniforme est la version continue de l'équiprobabilité
On considère une variable aléatoire X qui peut prendre n'importe quelle valeur d'un intervalle [a ; b] : il y en a une infinité... Sa loi de probabilité est dite continue et se caractérise par une fonction de densité.
X suit la loi uniforme sur un intervalle [a;b] si sa fonction de densité est la fonction f définie sur [a;b] par
f(x)=b−a1
f(x)=\dfrac{1}{b-a}
f est continue et positive sur [a ; b] .
∫abf(x)dx=∫abb−a1dx=[b−a1x]ab
\displaystyle\int_{a}^{b}f(x)dx=\int_{a}^{b}\dfrac{1}{b-a}dx=\left[\dfrac{1}{b-a}x\right]_a^b
=b−ab−b−aa=b−ab−a=1
=\dfrac{b}{b-a}-\dfrac{a}{b-a}=\dfrac{b-a}{b-a}=1
f est bien une densiteˊ de de probabiliteˊ :
f\text{ est bien une densité de de probabilité :}
Ex. On suppose que X, le temps d’attente (en h) à l'entrée d'un musée suit la loi uniforme sur [0 ; 3].
La fonction de densiteˊ est f(x)=3−01=31
\text{La fonction de densité est }f(x)=\frac{1}{3-0}=\frac{1}{3}
Quelle est la probabilité d'attendre entre une et deux heures ?
p(X∈[1;2])=∫1231dx=[31x]12=32−31=31
p(X\in[1;2])=\displaystyle\int_{1}^{2}\dfrac{1}{3}dx=\left[\dfrac{1}{3}x\right]_1^2=\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}
Quelle est la probabilité d'attendre entre deux et trois heures ?
p(X∈[2;3])=∫2331dx=[31x]23=33−32=31
p(X\in[2;3])=\displaystyle\int_{2}^{3}\dfrac{1}{3}dx=\left[\dfrac{1}{3}x\right]_2^3=\dfrac{3}{3}-\dfrac{2}{3}=\dfrac{1}{3}
Quelle est la probabilité d'attendre entre 0 et une heure ?
31
\dfrac{1}{3}
On peut calculer les probabilités précédentes plus rapidement grâce à la propriété suivante :
Pour tout intervalle [c ; d] inclus dans [a ; b] on a :
p(c⩽X⩽d)=b−ad−c
p(c\leqslant X \leqslant d)=\dfrac{d-c}{b-a}
p(1⩽X⩽2)=3−02−1=31
p(1\leqslant X \leqslant 2)=\dfrac{2-1}{3-0}=\dfrac{1}{3}
Quelle est la probabilité d'attendre moins d'une heure et demie ?
p(0⩽X⩽1,5)=3−01,5−0=21
p(0\leqslant X \leqslant 1,5)=\dfrac{1,5-0}{3-0}=\dfrac{1}{2}
Soit X une variable aléatoire qui suit la loi uniforme sur [a ; b]. Alors l'espérance de X est
E(X)=2a+b
E(X)=\dfrac{a+b}{2}
Si on reprend l'exemple du temps d'attente :
E(X)=20+3=1,5
E(X)=\dfrac{0+3}{2}=1,5
Interprétation : Si l'on visite souvent ce musée, on peut "espérer" un temps d'attente moyen d'une heure et demie.
Exercices
Calculatrice
p(5,5⩽X⩽7)=7−37−5,5=41,5=0,375
p(5,5\leqslant X \leqslant 7)=\dfrac{7-5,5}{7-3}= \dfrac{1,5}{4}= 0,375
p(X⩽6)(X⩾4)=p(X⩽6)p(4⩽X⩽6)
p_{(X\leqslant6)}( X \geqslant 4)=\dfrac{p(4\leqslant X \leqslant 6)}{p( X \leqslant 6)}
p(4⩽X⩽6)=7−36−4=42
p(4\leqslant X \leqslant 6)=\frac{6-4}{7-3}= \frac{2}{4}
p(X⩽6)=7−36−3=43
p( X \leqslant 6)=\frac{6-3}{7-3}= \frac{3}{4}
p(X⩽6)(X⩾4)=4342=42×34=32
p_{(X\leqslant6)}( X \geqslant 4)=\frac{\frac{2}{4}}{\frac{3}{4}}=\frac{2}{4}\times \frac{4}{3}=\frac{2}{3}
p(X⩽6)(X⩾4)=p(X⩽6)p(4⩽X⩽6)
p_{(X\leqslant6)}( X \geqslant 4)=\dfrac{p(4\leqslant X \leqslant 6)}{p( X \leqslant 6)}
=32
=\frac{2}{3}
Plus rapide :
On compte les carreaux...
Soit X la variable aléatoire correspondant à l'heure d'arrivée de Fatou. X suit la loi uniforme sur [7 ; 8,5].
p(X<8)=8,5−78−7=1,51=32
p( X<8)=\dfrac{8-7}{8,5-7}= \dfrac{1}{1,5}= \dfrac{2}{3}
p(8⩽X⩽8,25)=8,5−78,25−8=1,50,25=61
p(8 \leqslant X \leqslant 8,25)=\dfrac{8,25-8}{8,5-7}= \dfrac{0,25}{1,5}= \dfrac{1}{6}
p(X>8)(X⩽8,25)=p(X>8)p(8<X⩽8,25)=3161=21
p_{(X>8)}( X \leqslant 8,25)=\dfrac{p(8< X \leqslant 8,25)}{p( X >8)}=\dfrac{\frac{1}{6}}{\frac{1}{3}}=\frac{1}{2}
Ex. type bac...
À 20 h, le groupe de touristes fait une pause autour d’un point d’eau pour observer le bain des éléphants. On considère que le temps d’attente en minute nécessaire pour observer des éléphants suit la loi uniforme sur l’intervalle [0 ; 90].
- Quelle est la probabilité que le groupe attende plus d’une heure avant d’apercevoir les éléphants ?
- Calculer l’heure moyenne d’arrivée des éléphants.
1. Si on appelle T la variable aléatoire qui donne le temps d’attente, la probabilité que le groupe attende plus d’une heure avant d’apercevoir les éléphants est
p(60<T⩽90)=90−090−60=9030=31
p(60< T \leqslant 90)=\dfrac{90-60}{90-0}= \dfrac{30}{90}= \dfrac{1}{3}
2. On calcule l'espérance de T :
E(T)=20+90=45
E(T)=\dfrac{0+90}{2}=45
L'observation débute à 20 h donc l’heure moyenne d’arrivée des éléphants est 20 h 45.
Ex. type bac...
Anne prévoit d’appeler Benoît par téléphone à un moment choisi au hasard entre 8 h 30 et 10 h.
Benoît sera dans un train à partir de 9 h pour un trajet de plusieurs heures. Quelle est la probabilité qu’Anne appelle Benoît alors qu’il est dans le train ?
On note T la variable aléatoire indiquant à quelle heure l’appel est passé. T suit une loi uniforme sur l’intervalle [8,5 ; 10].
p(T⩾9)=10−8,510−9=1,51=32
p(T \geqslant 9)=\dfrac{10-9}{10-8,5}= \dfrac{1}{1,5}= \dfrac{2}{3}
p(9⩽T⩽10)
p(9\leqslant T \leqslant 10)
Ex. type bac...
Dans un hôtel, le petit déjeuner n’est servi que jusqu’à 10 h 15. Pierre, qui réside dans cet hôtel, se lève entre 9 h et 11 h.
On admet que l’heure de lever de Pierre est modélisée par une variable aléatoire qui suit la loi uniforme sur l’intervalle [9 ; 11]. La probabilité que Pierre ne puisse pas prendre son petit déjeuner est 0,425. Vrai ou Faux ?
Soit T la variable aléatoire qui donne l’heure du lever de Pierre. Pour que Pierre ne puisse pas prendre son petit déjeuner, il faut qu’il se lève entre 10h15 (soit 10,25 h) et 11 heures.
p(10,25⩽T⩽11)=11−911−10,25=0,375
p(10,25\leqslant T \leqslant 11)=\dfrac{11-10,25}{11-9}=0,375
Affirmation fausse.
Loi uniforme sur [0 ; 10]
Loi exponentielle
Calculatrice
Loi exponentielle
de paramètre λ=0,05
Lois à densité Lois à densité Loi uniforme sur [ a ; b ] Loi exponentielle sur [ 0 ; + ∞ [
Lois continues
By Jean-Marc Kraëber
Lois continues
Lycée Saint-Exupery
- 965
