Variables aléatoires discrètes
Rappels :
On définit une variable aléatoire lorsque l'on associe des nombres aux issues d'une expérience aléatoire.
Ex. Le gain algébrique à un jeu de hasard est une variable aléatoire.
Ex. Le jeu pile ou face est une épreuve de Bernoulli dans laquelle le succès peut être "obtenir face".
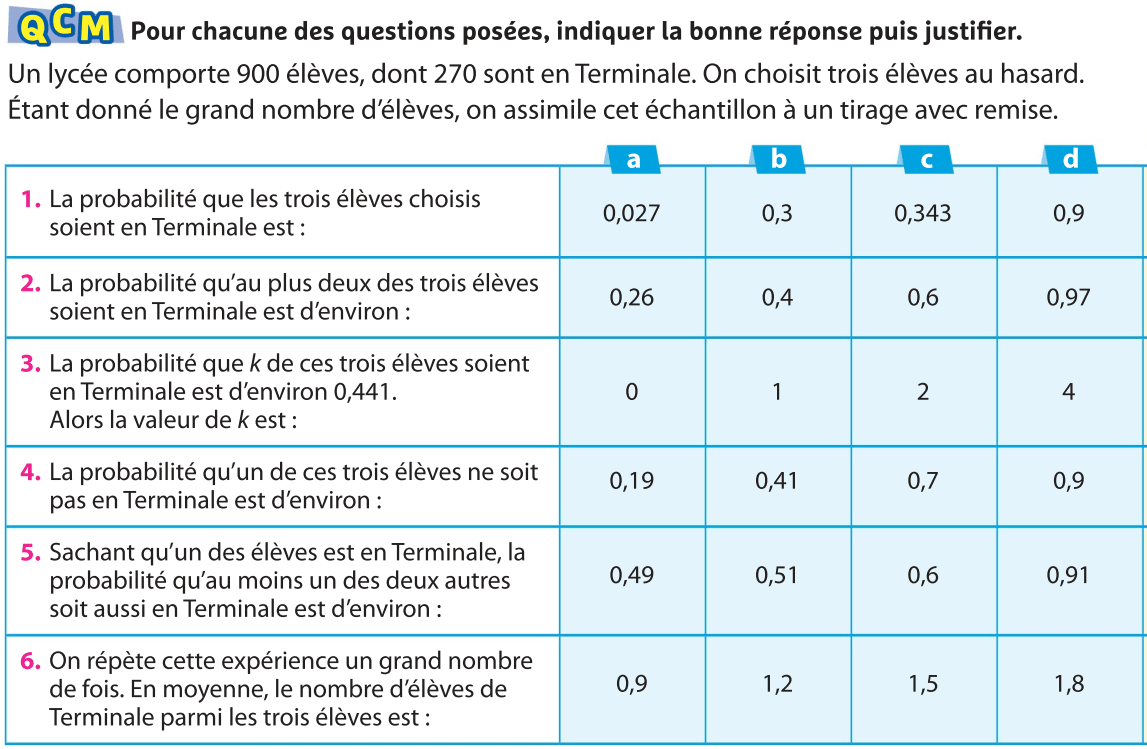
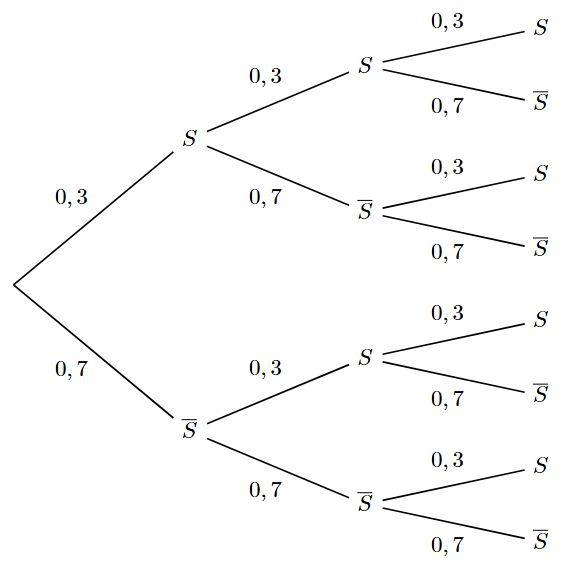
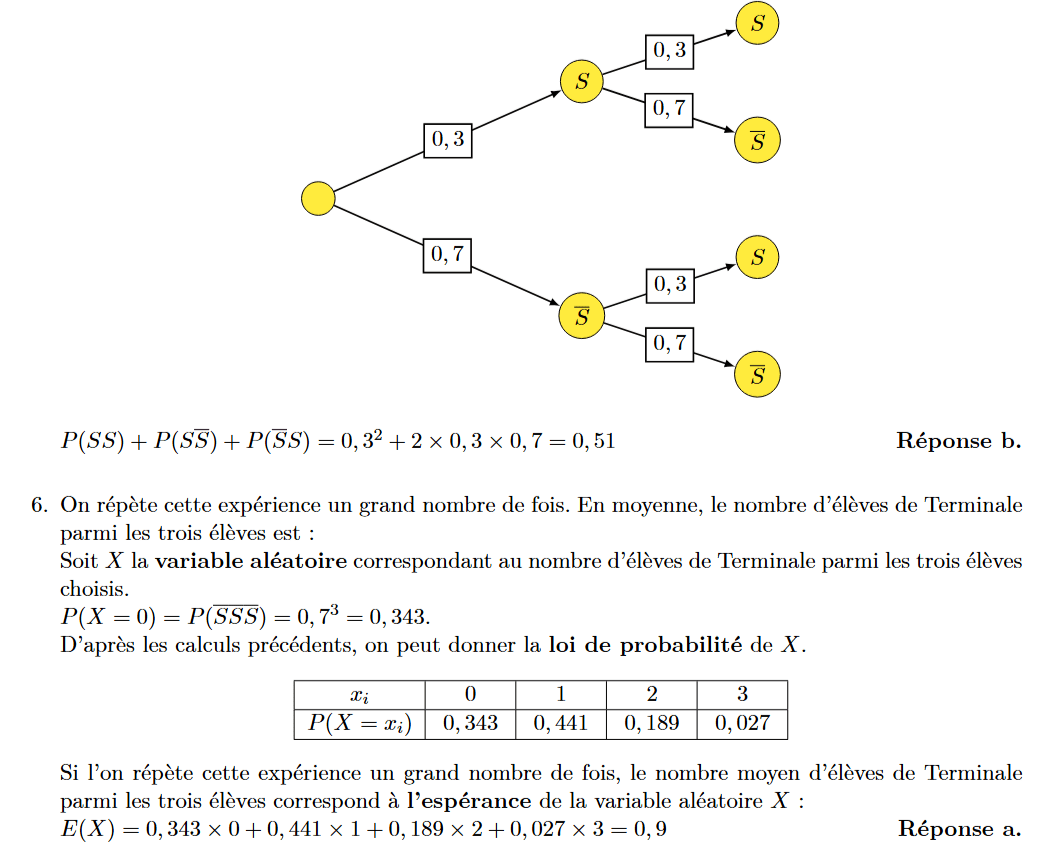
Exercices :
E(X)=p_1x_1+p_2x_2+p_3x_3
E(X)=0,2\times 2+ 0,7\times 6+0,1\times 9
E(X)=5,5
0,25
E(Y)=0,6\times (-13)+ 0,25\times(-7)+0,15\times 12=-7,75
2 couleurs : Rouge et noir
4 familles : Trèfle, Pique, Cœur et Carreau
13 cartes par famille dont 3 figures (valet, dame, roi)
Première question à se poser :
Quelles valeurs peut prendre la variable aléatoire ?
Deuxième question à se poser :
Quelle probabilité est associée à chaque valeur ?
1\,;5\,;10\,;20
Loi de probabilité :
E(X)=\dfrac{8}{13}\times 1+ \dfrac{1}{13}\times 5+\dfrac{3}{13}\times 10+\dfrac{1}{13}\times 20=\dfrac{63}{13}
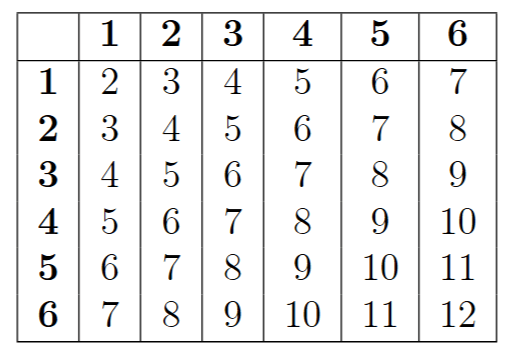
Quelles valeurs peut prendre la variable aléatoire ?
Quelle probabilité est associée à chaque valeur ?
2\,;3\,;4\,;\dots;12
Indication : Faire un tableau avec des colonnes pour les valeurs de 2 à 12.
Loi de probabilité :
Espérance de la variable aléatoire :
E(X)=\frac{1}{36}\times 2+\frac{2}{36}\times 3+\dots+\frac{1}{36}\times 12=7
Mode statistique de la calculatrice :
\begin{pmatrix} n\\ 0 \end{pmatrix}=1
\begin{pmatrix} n\\ n\end{pmatrix}=1
\begin{pmatrix} n\\ n-1\end{pmatrix}=n
\begin{pmatrix} n\\ 1\end{pmatrix}=n
\begin{pmatrix} n-1\\ k-1 \end{pmatrix}+\begin{pmatrix} n-1\\ k \end{pmatrix}=\begin{pmatrix} n\\ k \end{pmatrix}
\text{donc }\begin{pmatrix} 12\\ 4 \end{pmatrix}=165+330=495
\text{donc }\begin{pmatrix} 12\\ 5\end{pmatrix}=330+462=792
\text{donc }\begin{pmatrix} 13\\ 5\end{pmatrix}=495+792=1287
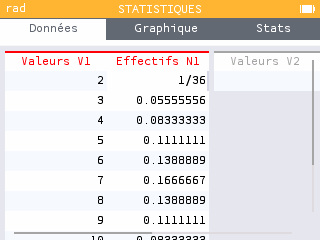
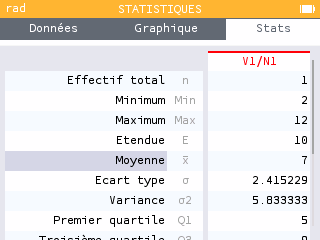
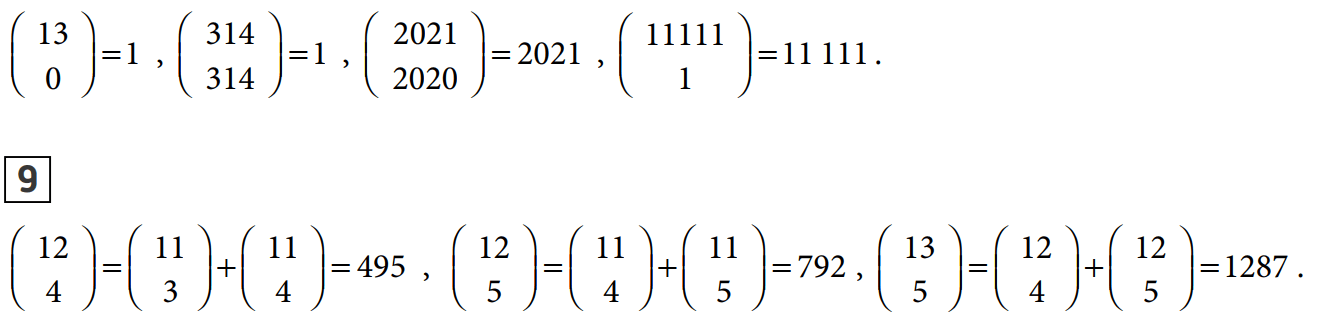
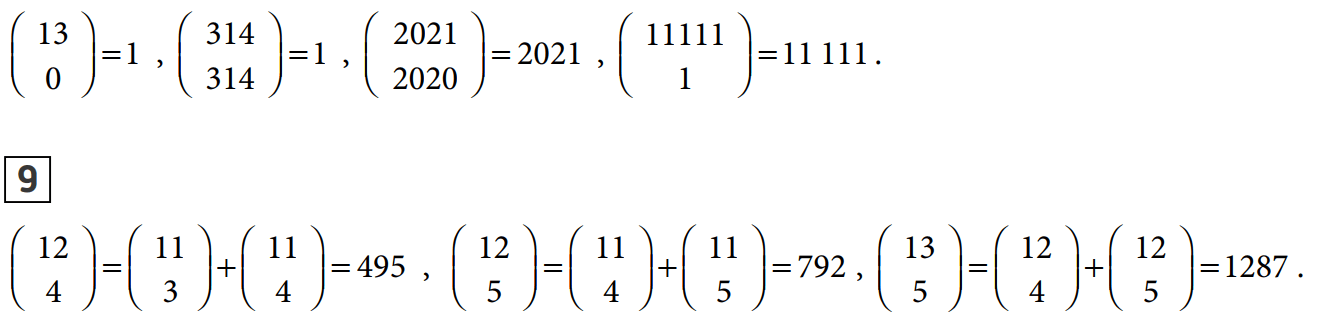
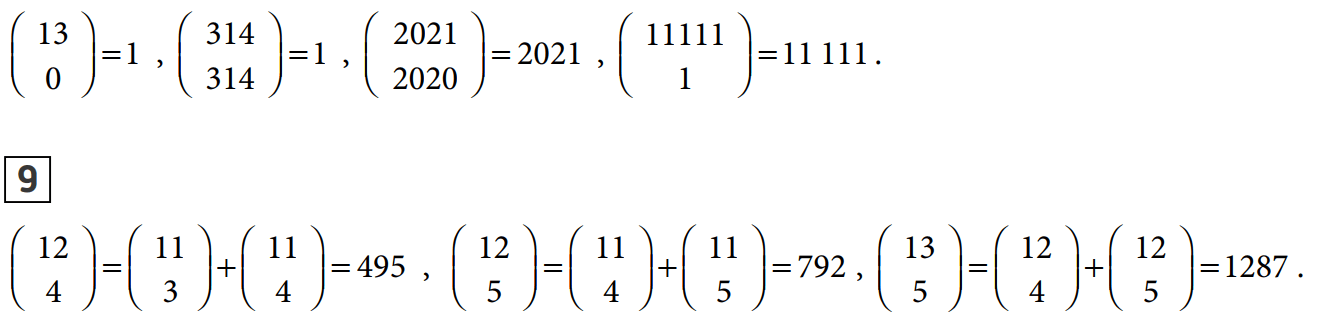
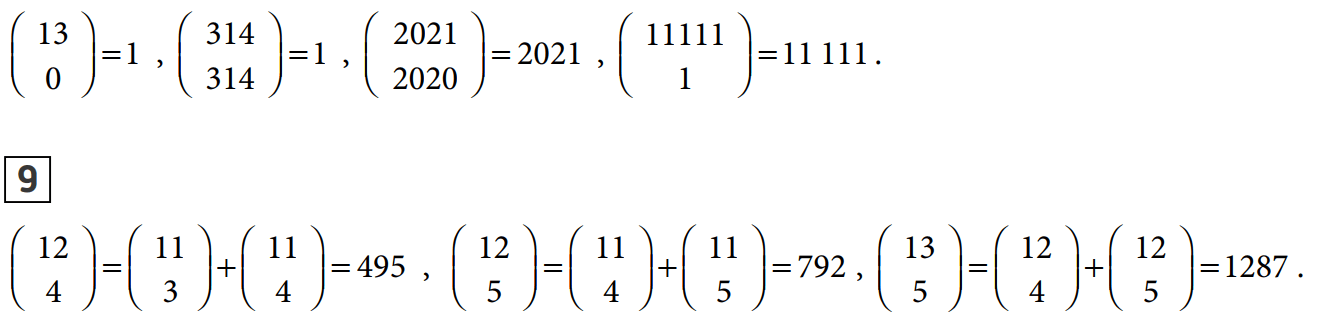
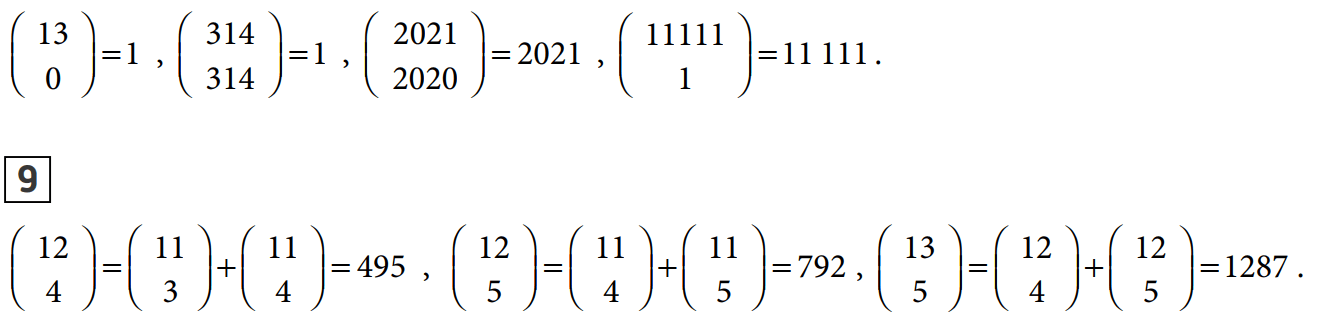
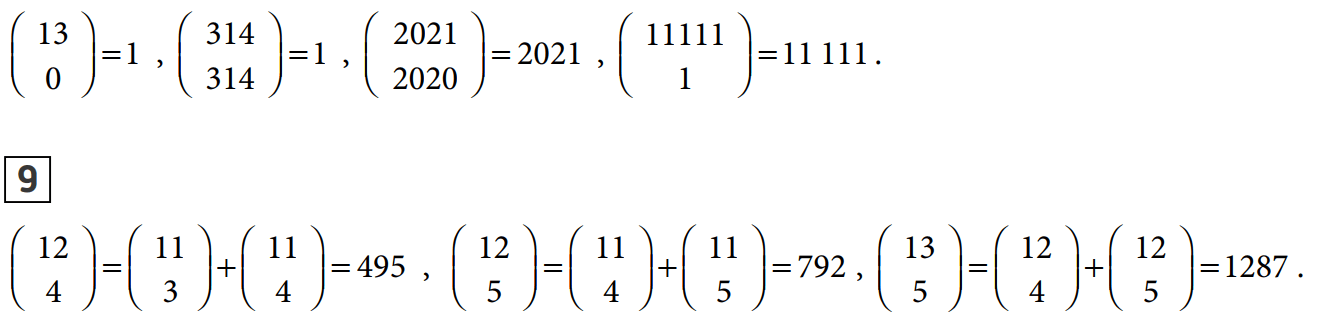
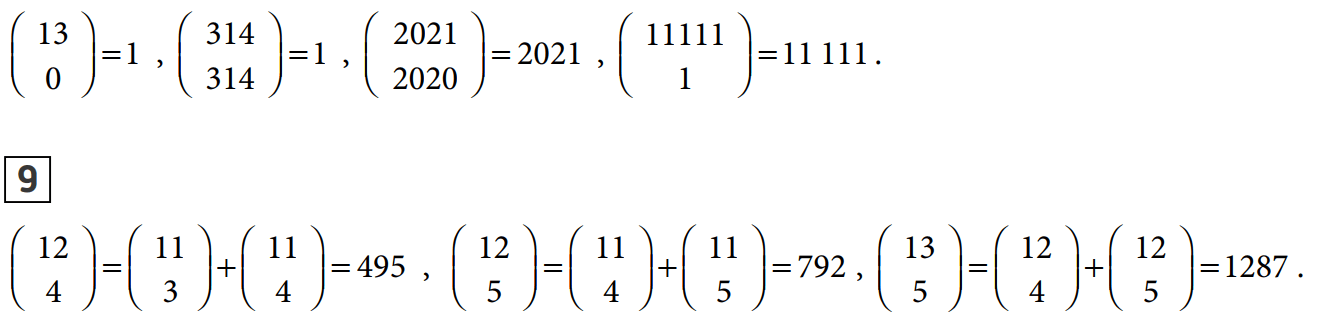
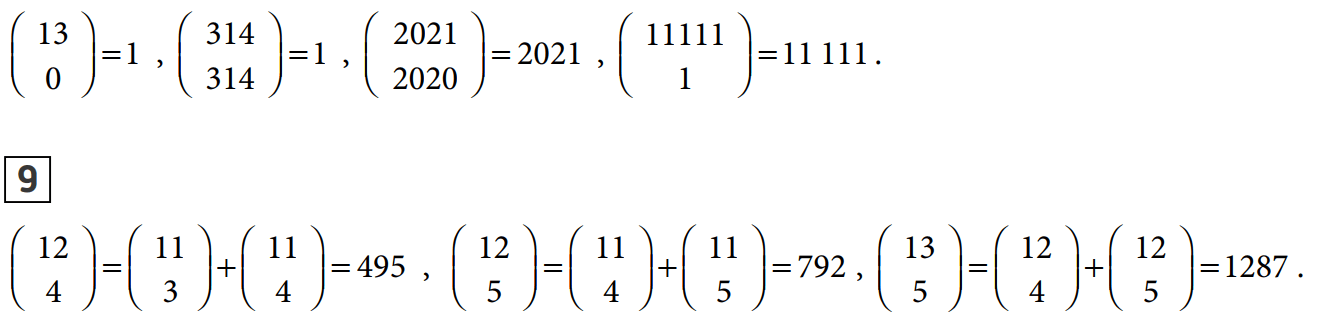
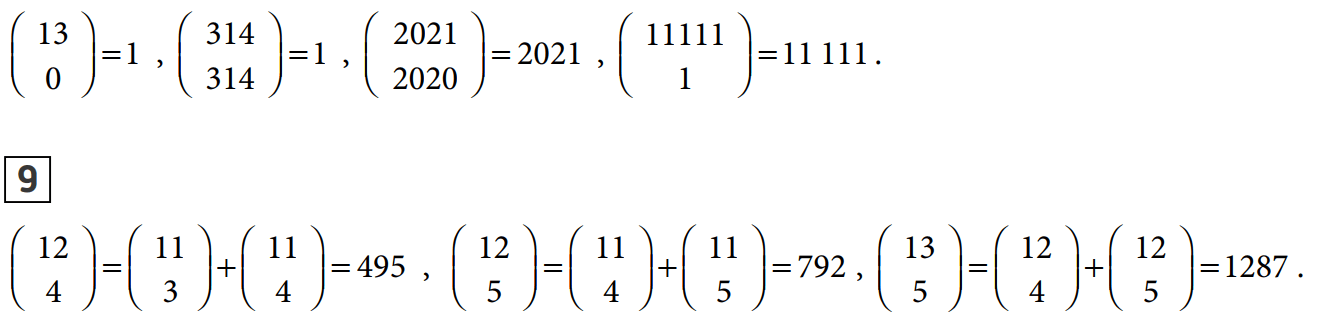
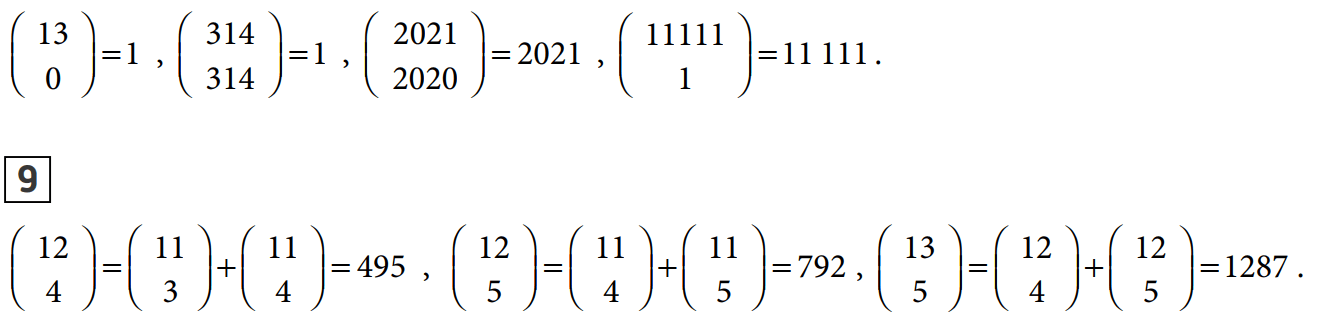
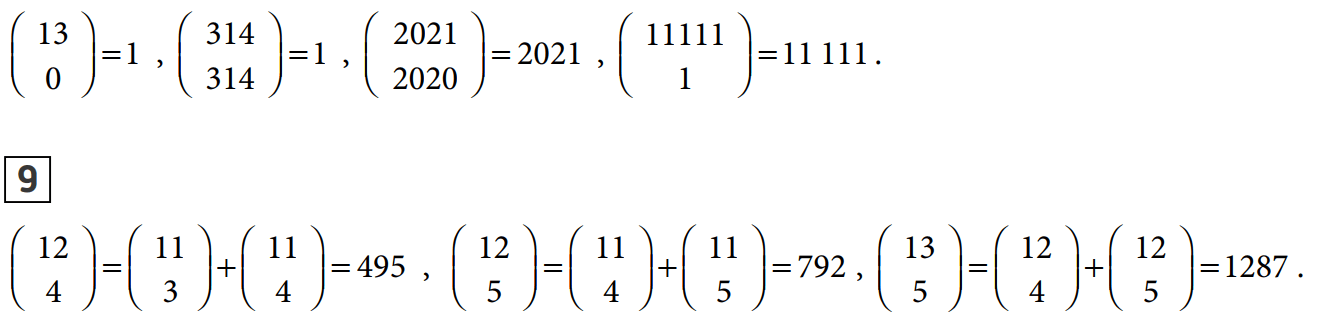
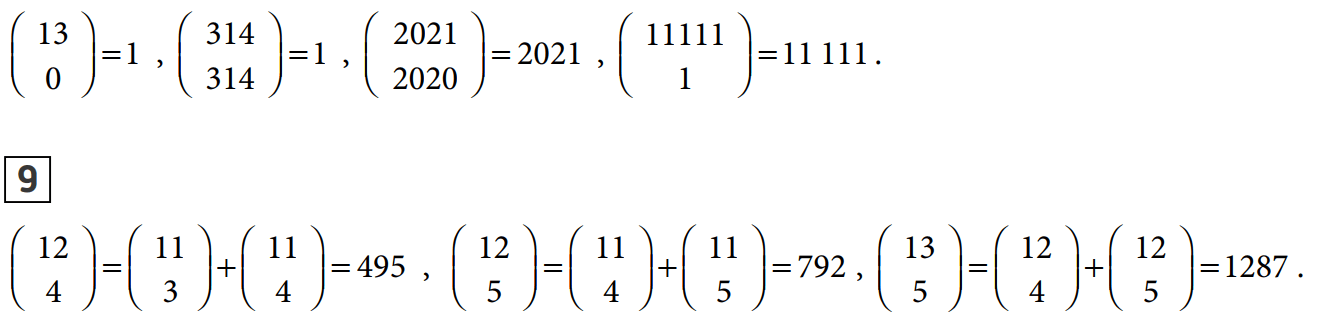
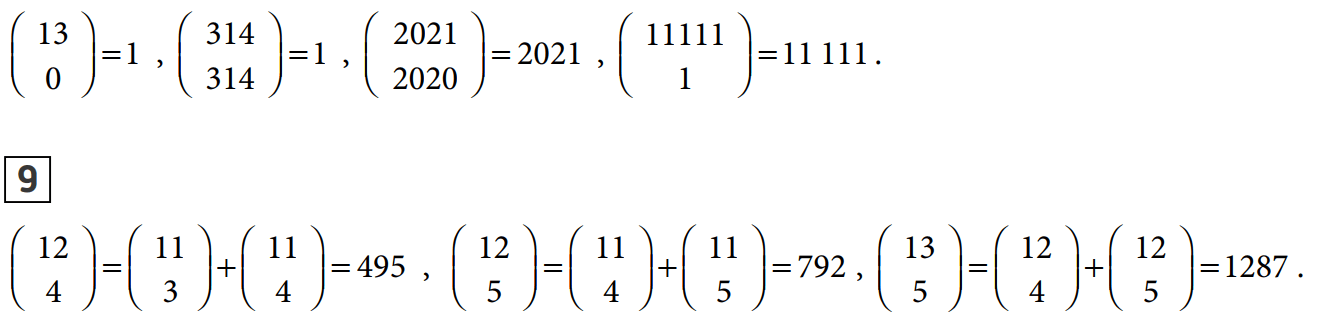
Vérifier avec la calculatrice : Boîte à outils (paste)
|
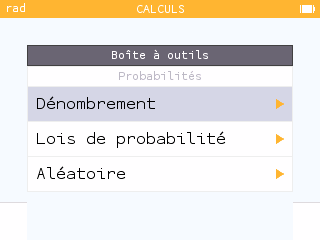
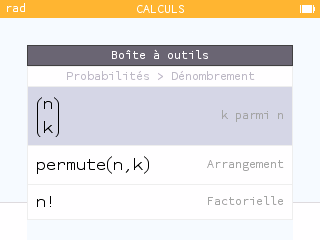
Un schéma de Bernoulli de paramètres n et p est la répétition de n épreuves de Bernoulli de paramètre p identiques et indépendantes. |
Vocabulaire :
Soit X la variable aléatoire correspondant au nombre de succès obtenus dans un schéma de Bernoulli de paramètres n et p.
La loi de probabilité de X est appelée loi binomiale de paramètres n et p. On la note : B(n ; p).
P(X=k)=\begin{pmatrix} n\\ k \end{pmatrix}\times p^k\times (1-p)^{n-k}
Probabilité d'obtenir k succès :
P(X=k)=\begin{pmatrix} n\\ k \end{pmatrix}\times p^k\times (1-p)^{n-k}
P(X=1)=\begin{pmatrix} 3\\ 1 \end{pmatrix}\times 0,3^1\times (1-0,3)^{3-1}
P(X=1)=3\times 0,3\times 0,7^{2}\approx 0,44
P(X=3)=\begin{pmatrix} 3\\ 3 \end{pmatrix}\times 0,3^3\times 0,7^{3-3}
P(X=3)=1\times 0,027\times 1\approx 0,03
Vérifier avec la calculatrice : Menu Probabilités
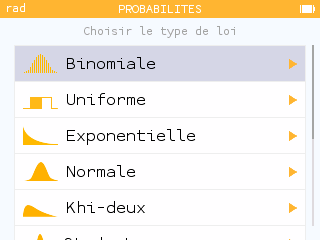
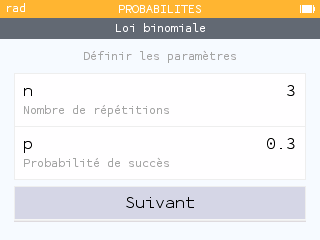
Vérifier avec la calculatrice : Menu Probabilités
P(X<3)=P(X\leqslant 2)
P(X<3)\approx 0,17
P(X=3)\approx 0,21
P(X<3)=P(X=0)+P(X=1)+P(X=2)
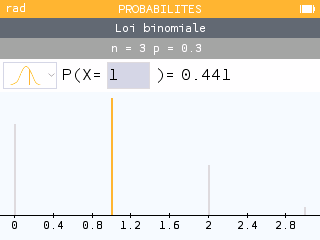
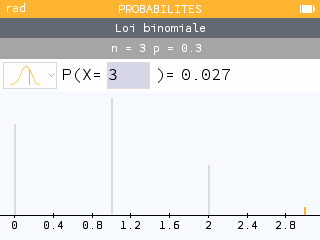
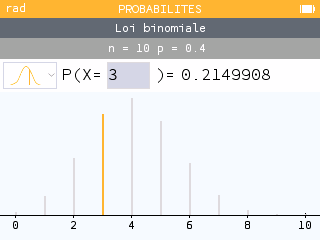
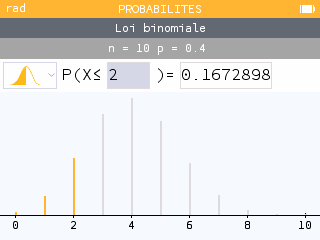
ou
P(X=5)\approx 0,21
P(X\geqslant 6)\approx 0,68
P(X=72)\approx 0,091
P(X\geqslant 72)\approx 0,115
P(X=9)\approx 0,043
P(X\leqslant 7)\approx 0,004
P(X=12)\approx 0,250
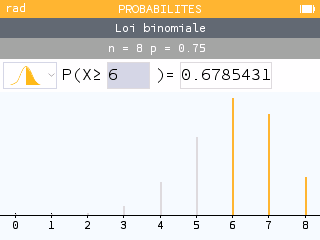
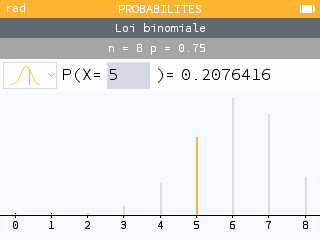
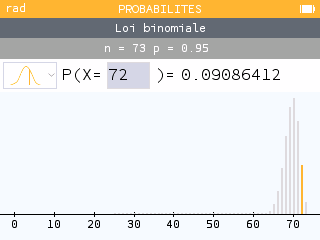
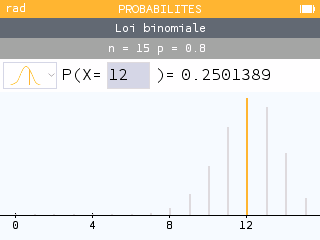
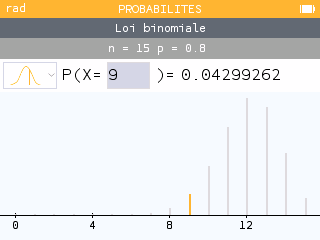
Espérance d'une loi binomiale :
Soit X une variable aléatoire qui la loi binomiale de paramètres n et p :
E(X) = np
E(X) = 35\times 0,2 = 7
E(X) = 30\times 0,75 = 22,5
E(X) = 52\times 0,19 = 9,88
E(X) = 45\times 0,2 = 9
E(Y) = 30\times 0,3 = 9
E(X) = E(Y)
\text{Oui, avec par exemple }n=100 \text{ et p = 0,002}.
(arrondies à 0,01 près)
P(X=k)=\begin{pmatrix} n\\ k \end{pmatrix}\times p^k\times (1-p)^{n-k}
1.\;P(X=2)=\begin{pmatrix} 9\\ 2\end{pmatrix}\times 0,3^2\times 0,7^{9-2}
P(X=2)=36\times 0,09\times 0,7^{7}\approx 0,267
2.\;P(X=4)=\begin{pmatrix} 9\\ 4\end{pmatrix}\times 0,3^4\times 0,7^{9-4}
P(X=4)=126\times 0,0081\times 0,7^{5}\approx 0,172
P(X=1)\approx 0,21
P(X\geqslant13)\approx 0,58
1.\;P(X=0)=0,6^{12}\approx 0,002
P(X=1)=12\times 0,4\times 0,6^{11}\approx 0,017
P(X=2)=\begin{pmatrix} 12\\ 2\end{pmatrix}\times 0,4^2\times 0,6^{10}\approx0,064
2.\;P(X\geqslant3)=1-P(X<3)
=1-(P(X=0)+P(X=1)+P(X=2))
\approx1-(0,002+0,017+0,064)
\approx0,917
3.\;P_{X\leqslant 8}(X\geqslant2)=\dfrac{P(2\leqslant X\leqslant 8)}{P(X\leqslant 8)}\approx \dfrac{0,965}{0,985}\approx 0,980
4.\;P_{X>5}(X\leqslant10)=\dfrac{P(5< X\leqslant 10)}{P(X>5)}=\dfrac{P(6\leqslant X\leqslant 10)}{P(X\geqslant 6)}
\approx \dfrac{0,334}{0,335}
\approx 0,997
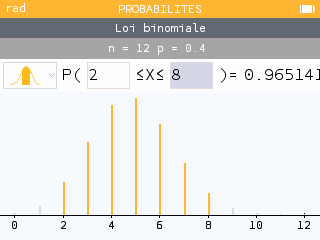
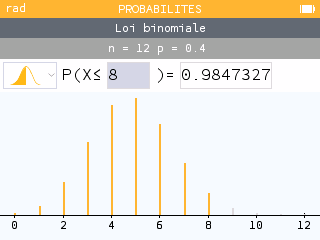
1. X suit une loi binomiale de paramètres n = 6 et p = 0,7.
2.\;P(X=4)\approx 0,324
P(X\geqslant4)\approx 0,744
3.\;P_{X\geqslant 2}(X\leqslant 4)=\dfrac{P(2\leqslant X\leqslant 4)}{P(X\geqslant 2)}\approx \dfrac{0,569}{0,989}\approx 0,575
1.
d.
Variables aléatoires discrètes
By Jean-Marc Kraëber
Variables aléatoires discrètes
Lycée Saint-Exupery - La Rochelle
