Elle est confondue avec d.
Faux : Soit a, l'abscisse du point A et f, la fonction représentée par C.
Le coefficient directeur de T est \(f'(a)\), le nombre dérivé de f en a et non \(f(a)\), l'ordonnée du point A.
Variation instantanée - Nombre dérivé
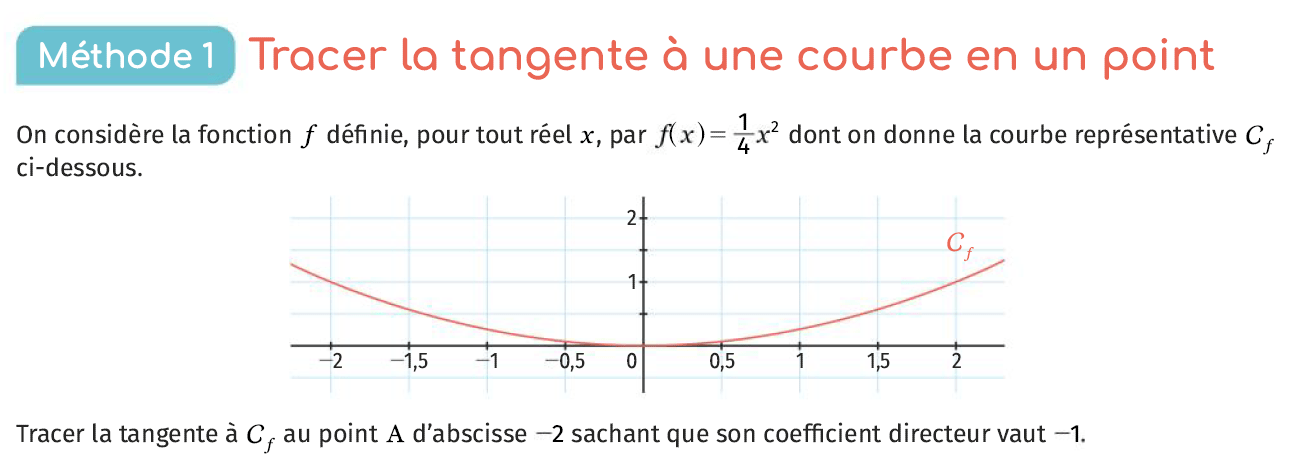
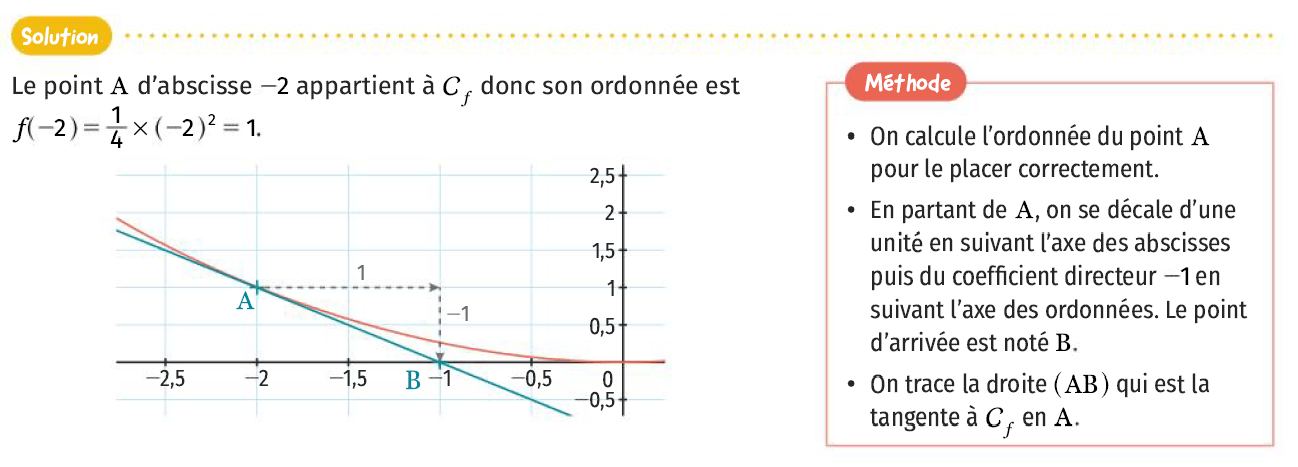
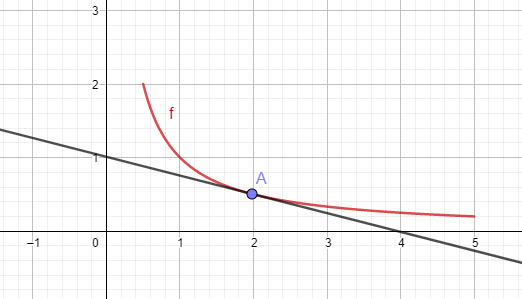
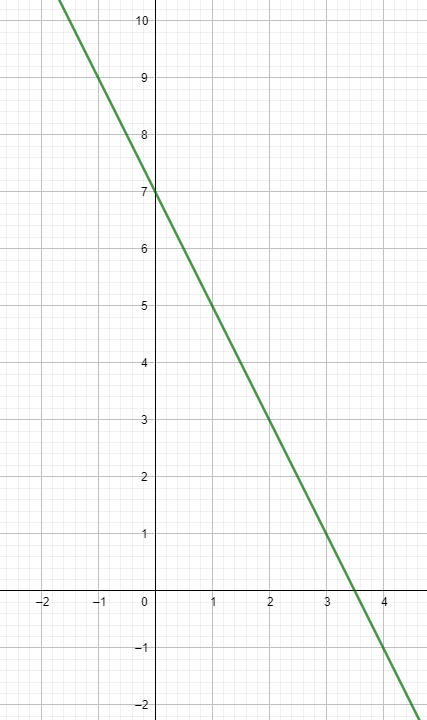
Le coefficient directeur est \(-0,25=-\dfrac{1}{4}\) ce qui signifie que lorsque l’on se déplace d’une unité vers la droite sur la tangente, l’ordonnée diminue de \(0,25\). On obtient ainsi la tangente suivante, passant par les points de coordonnées \((0\,;1)\) et \((4\,;0)\).
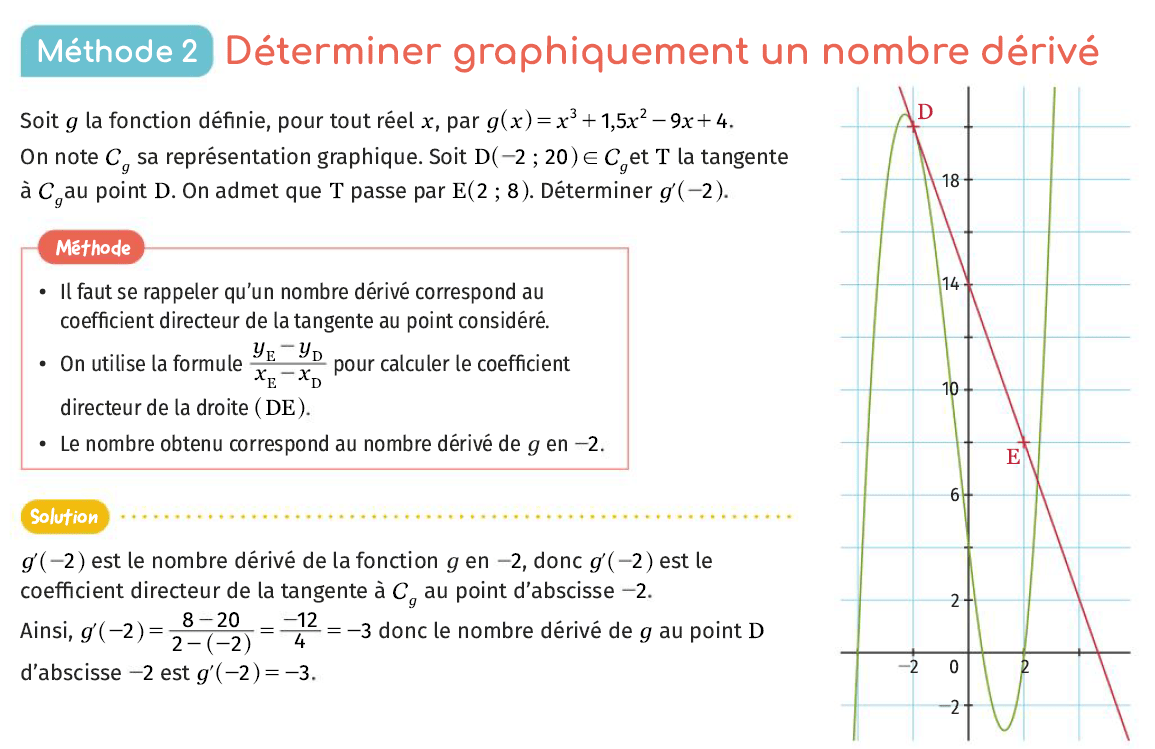
Si la tangente au point d’abscisse \(a\) est horizontale, alors son coefficient directeur vaut \(0\), donc \(f'(a)=0\).
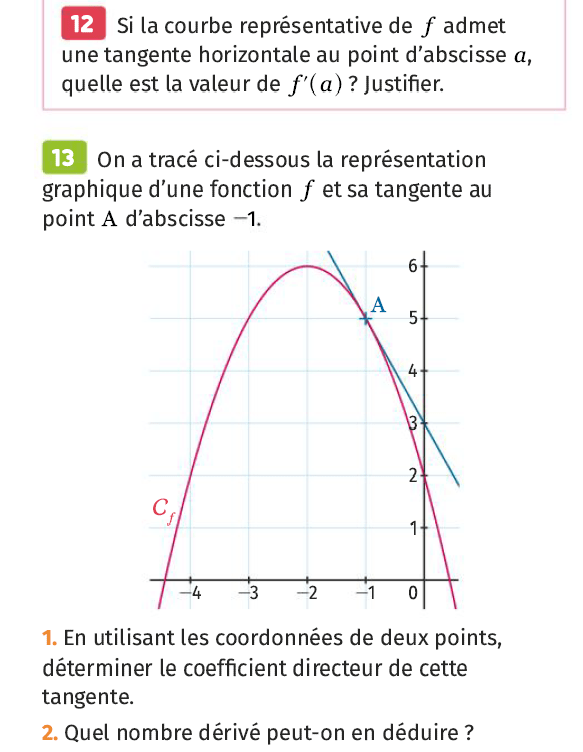
1) La tangente en \(A\) passe par les points \(A(-1\,;5)\) et \(B(0\,;3)\). Ainsi, le coefficient directeur de la tangente est \(\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{3-5}{0 - (-1)}=-2\).
2) On en déduit que \(f'(-1)=-2\).
f'(0)=4
f'(2)=0
f'(3)=-2
f'(2)=0
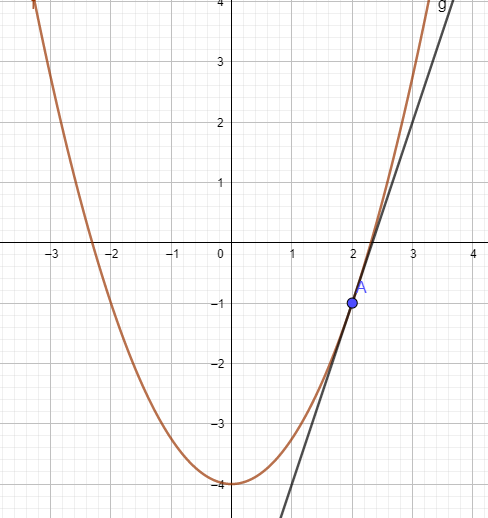
On commence par placer le point \(A(2\,;-1)\) par lequel la courbe doit passer. On trace également la droite passant par A et de coefficient directeur 3 qui devra être la tangente à la courbe au point A. On trace enfin une courbe possible. On obtient par exemple la courbe ci-dessous.
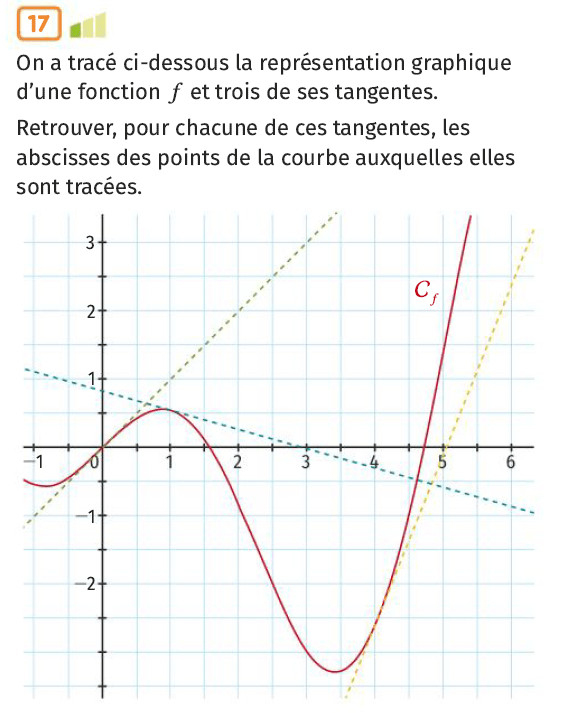
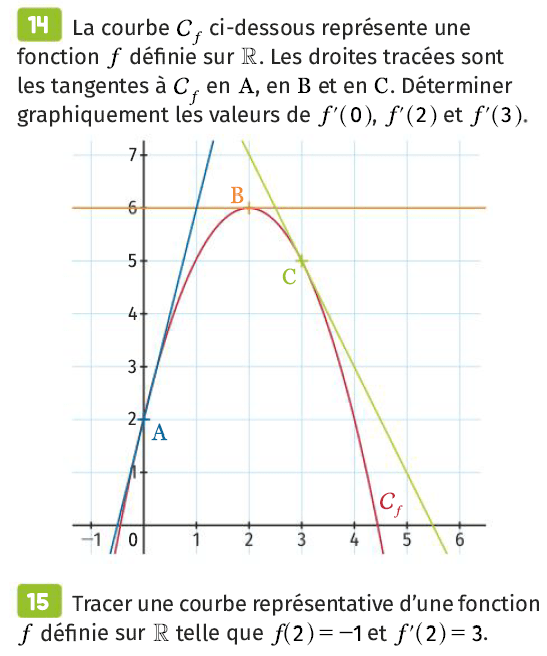
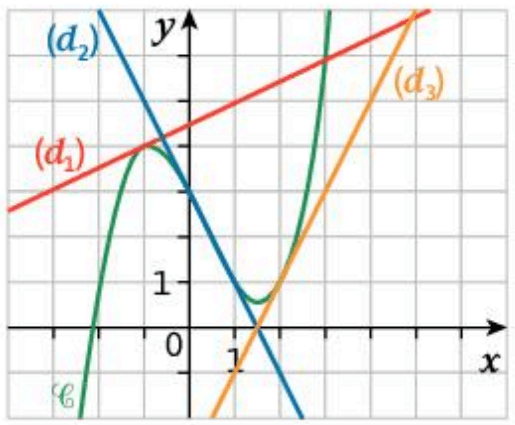
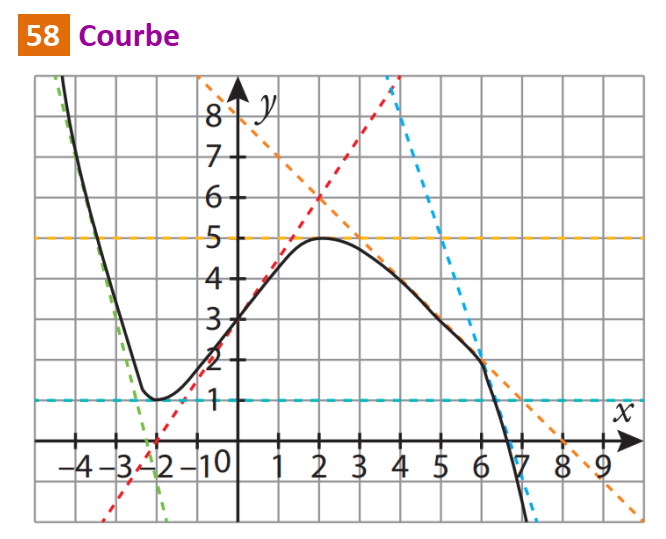
La droite verte est la tangente à la courbe représentative de \(f\) au point d’abscisse 0.
La droite bleue est la tangente à la courbe représentative de \(f\) au point d’abscisse 1.
La droite jaune est la tangente à la courbe représentative de \(f\) au point d’abscisse 4.
1,5
1,5
2
-3
-1,5
\dfrac{-3}{2}=-1,5
1,5
-1,5
0,5
1,5
2
-1,5
-1,5
0,5
-0,75
\dfrac{-1,5}{2}=-0,75
1,5
-1,5
0,5
-0,75
0,6
1,5
0
-1,5
0,5
-0,75
0,6
0
1,5
-1,5
0,5
-0,75
0,6
0
0,75
1,5
2
0,75
-1,5
0,5
-0,75
\dfrac{0,75}{2}=0,375
0,6
0
0,75
0,375
1,5
-1,5
0,5
-0,75
0,6
0
0,75
0,375
1,3
1,5
1,5
1,3
-1,5
0,5
-0,75
\dfrac{1,3}{1,5}\approx0,87
0,6
0
0,75
0,375
1,3
0,87
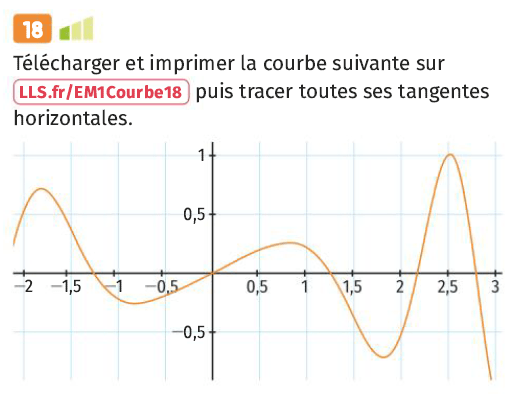
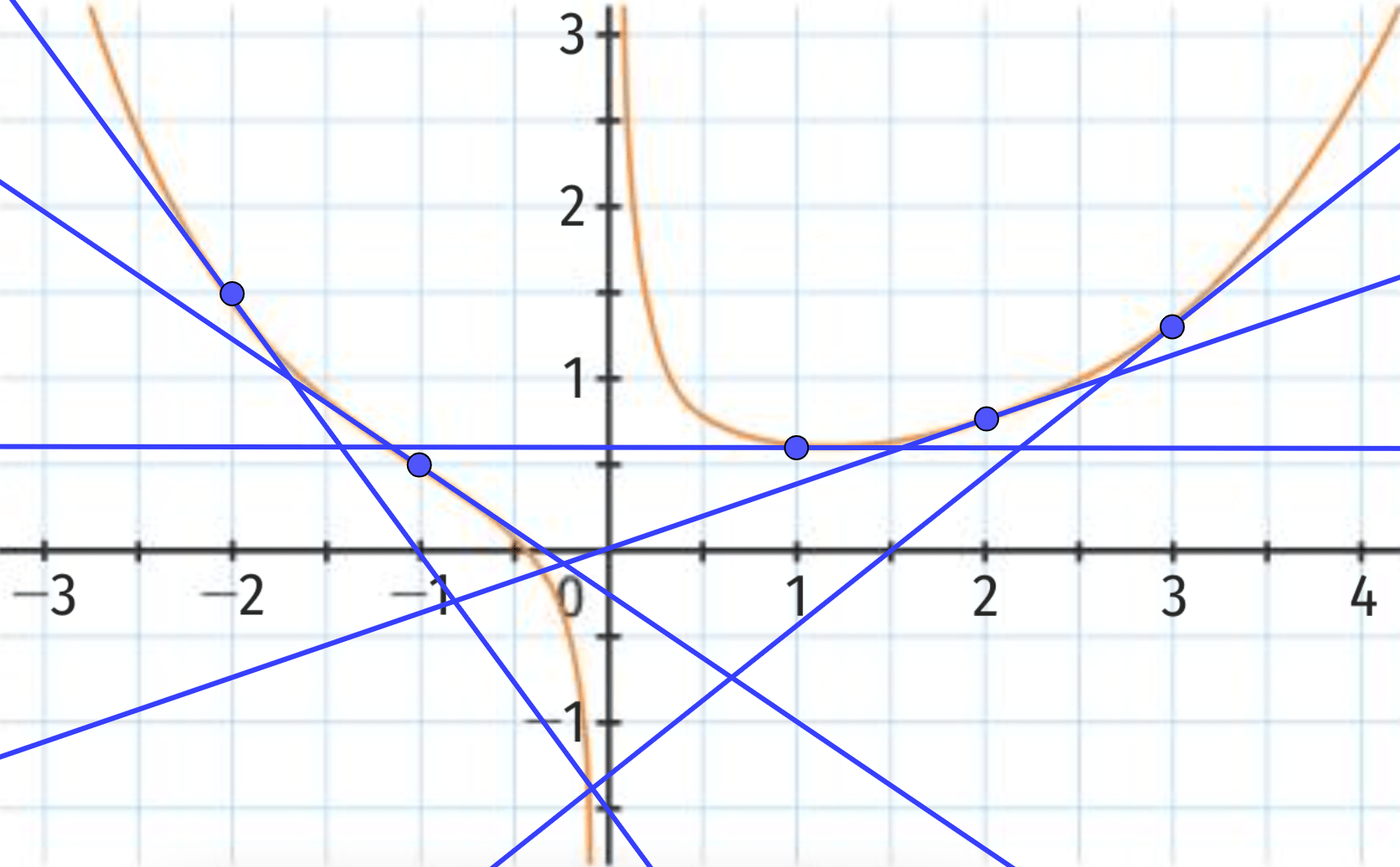
b. La tangente à la courbe de \( f \) au point d’abscisse \(3\) est en fait confondue avec la courbe représentative de \(f\) elle-même.
c. La valeur de \( f'(3) \) est le coefficient directeur de la tangente au point d'abscisse 3 donc, d’après la question précédente, le coefficient directeur de la droite représentant f, qui vaut \(-2\).
d. Au point d’abscisse \(-4\), la tangente est à nouveau confondue avec la courbe de \(f\), et \(f'(-4) \) vaut donc encore \(-2\).
Soit f une fonction de la forme \(f(x) = mx+p\). La courbe représentative de f est une droite car f est une fonction affine. Par conséquent, la tangente au point d’abscisse a est confondue avec la courbe représentative de f , qui est donc une droite, et \(f'(a)\) correspond à son coefficient directeur. Ce coefficient directeur vaut m et ainsi \(f'(a) = m\).
\(f'(−1) = f'(2)\) signifie que les tangentes à la courbe représentative de f aux points d’abscisses respectives \(-1\) et 2 ont le même coefficient directeur. Par conséquent, elles sont parallèles.
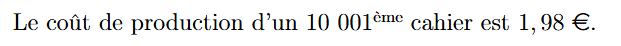
Exercice 1 (Questions de cours).
1. Quel est le lien entre nombre dérivé et tangente ?
Le nombre dérivé est le coefficient directeur de la tangente.
2. Comment se note le nombre dérivé d’une fonction f en un nombre réel a ?
\(f'(a)\)
3. Lorsqu’une fonction f modélise la position en fonction du temps d’un mobile animé d’un mouvement rectiligne, que représente \(f'(a)\) ?
La vitesse instantanée du mobile à l'instant a.
4. Donner l’équation de la tangente à la courbe d’une fonction f en un point d’abscisse a.
\(y=f'(a)(x-a)+f(a)\)
a
f(a)
f'(a)
\text{Vrai : }f'(0)=-2\text{ et }f'(2)=2
\text{Faux : }(d_1)\text{ est la tangente au point d'abscisse}-1.
\text{Vrai : }\text{ il n'y a que deux tangentes horizontales.}
\text{Faux : }f'(0)=-2
\text{Faux : }f'(4)=3
\text{Faux : le coefficient directeur de la tangente est égal à }2.
\text{Faux : l'équation correcte est }y = -2x + f(0).
\text{Nombre dérivé de }f \text{ en 2 : }f'(2)=1
\text{Equation de la tangente au point d'abscisse 2 : } y=x-1
f'(2) = \dfrac{y_B - y_A}{x_B - x_A} = \dfrac{-2 - 0}{6 - (-4)} = \dfrac{-2}{10} = -0,2.
\begin{align*}
0&= -0,2\times (-4) + p \\
p&=-0,8
\end{align*}
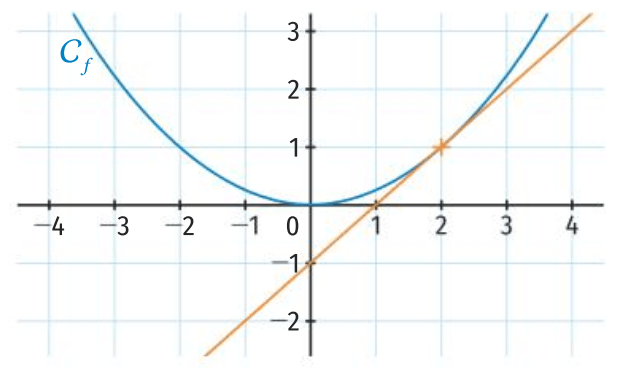
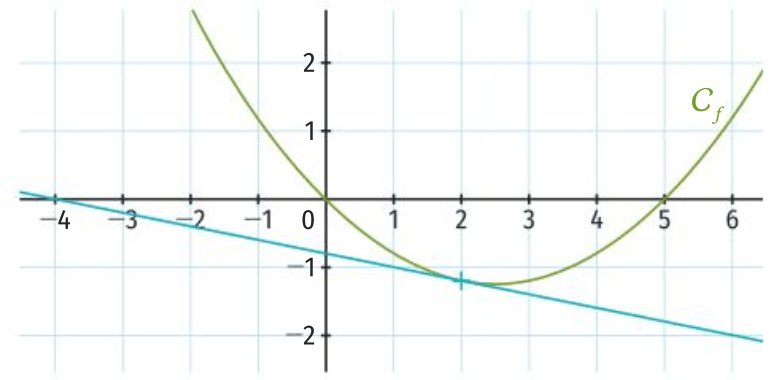
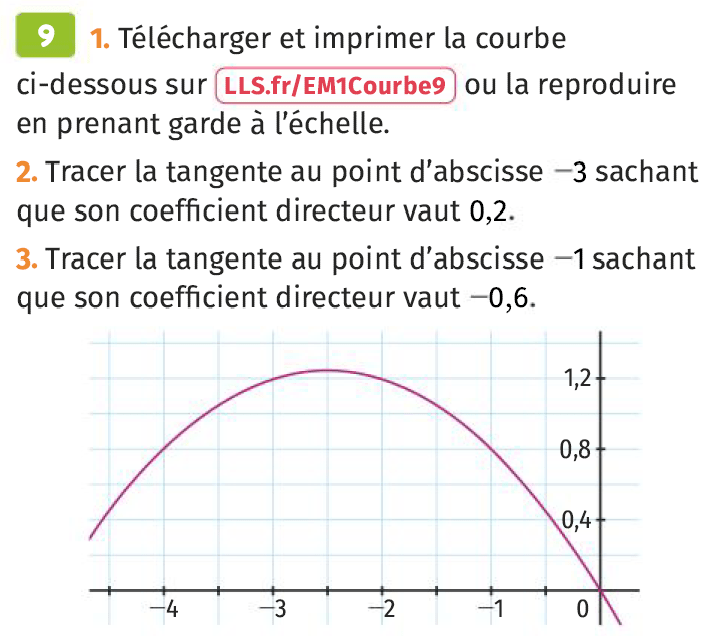
\(f'(x)=-0,2\) donc l'équation de la tangente à la courbe \(C_f\) au point d'abscisse 2 est de la forme \(y=-0,2x+p\).
La tangente passe par le point \(A(-4\,;0)\) donc
On en déduit que \(y=-0,2x-0,8\) est l'équation de la tangente à la courbe \(\mathcal{C}_f\) au point d'abscisse 2.
y = -x
y = f'(0)(x -0) + f(0)
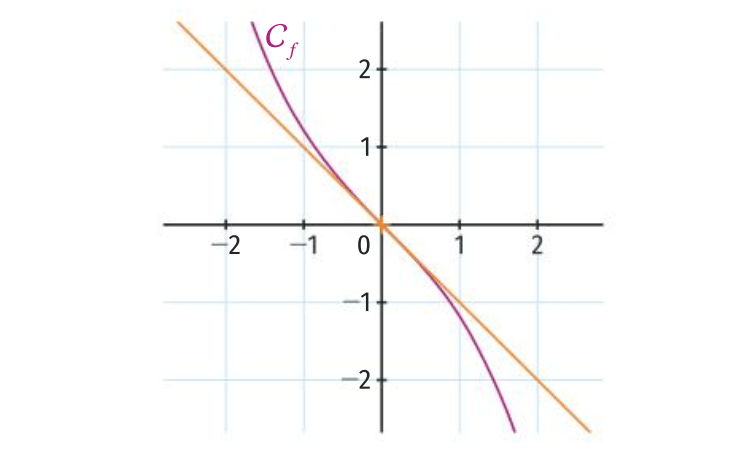
Avec \(f'(0) = -1\) et \(f(0) = 0\), on retrouve :
y = -x.
\dfrac{10}{5}=2
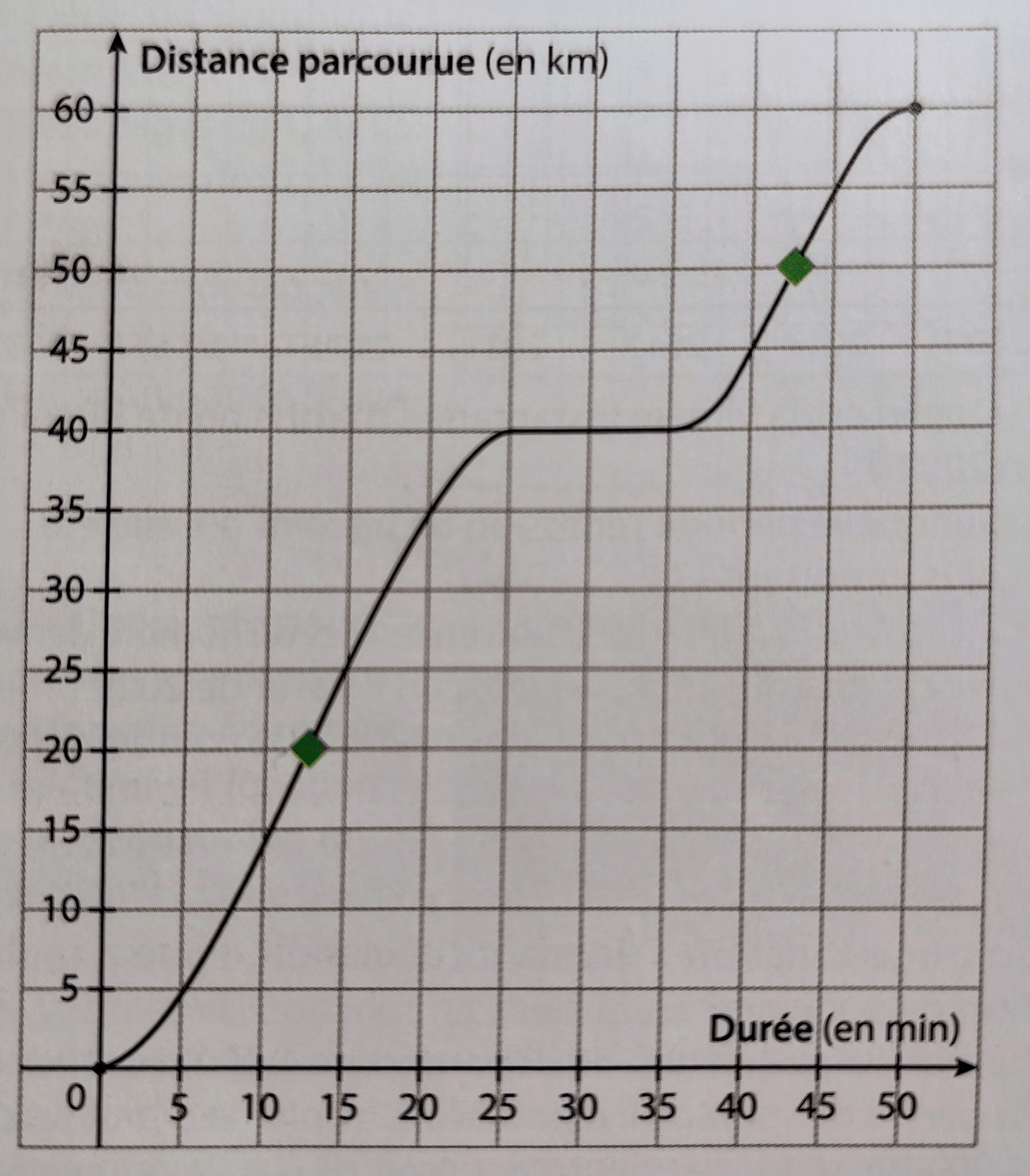
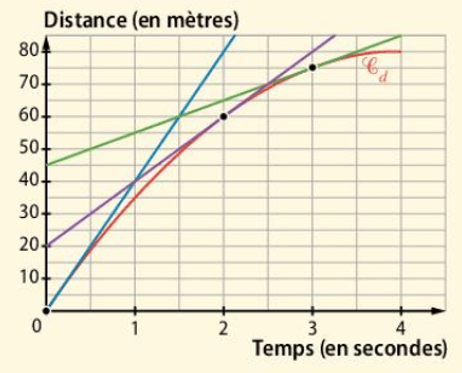
D'après la question précédente, la vitesse instantanée de la voiture est environ 2 km/min soit 120 km/h.
Oui.
Approximativement à 12,5 min et à 42,5 min.
\dfrac{50-20}{42,5-12,5}=1\text{ km/min}\text{ soit une vitesse moyenne de }60\text{ km/h.}
Non.
1. Dans le repère ci-dessous, placer les points correspondants de la courbe.
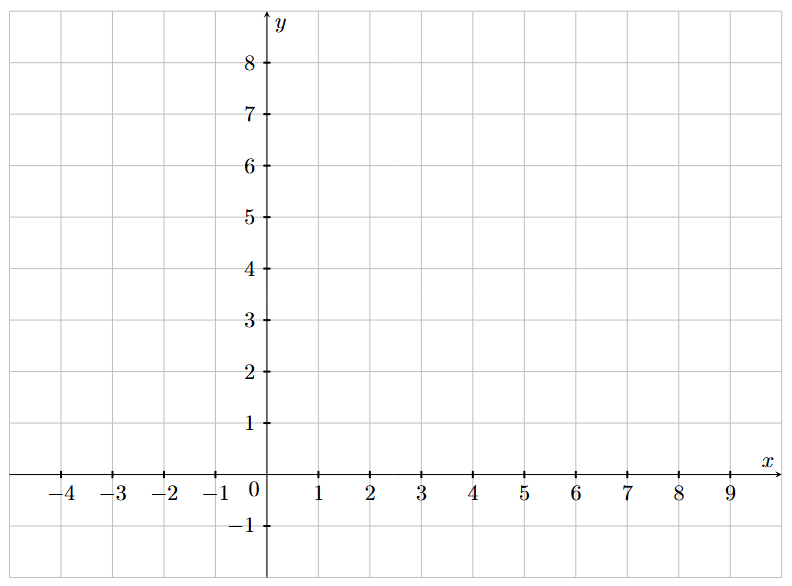
1. Dans le repère ci-dessous, placer les points correspondants de la courbe.
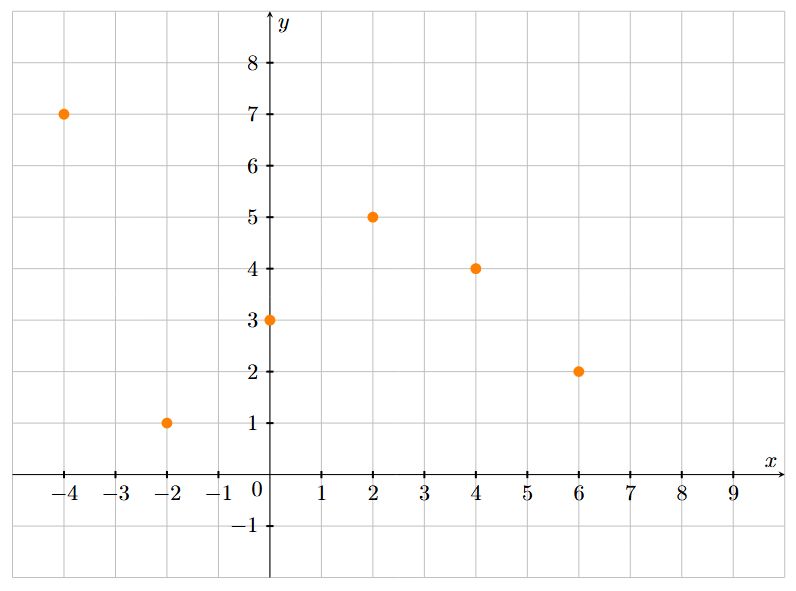
2. En chacun de ceux-ci, tracer la tangente à la courbe représentant la fonction h
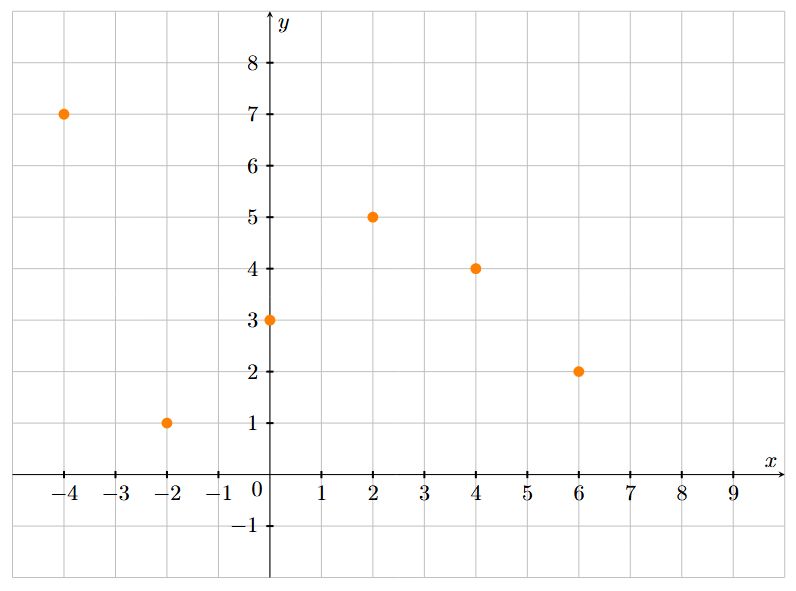
3. Tracer alors une allure possible de la courbe.
Variation instantanée
By Jean-Marc Kraëber
Variation instantanée
Lycée Saint-Exupery
