Reasoning Engines
A bird's eye view
Contents
- Intro
- Logic-based systems
- Arithmetic-based systems
- Local Search
- IDP
- DMN
Goal of "reasoning engine"?
"each doctor has at most one shift per day"
"a doctor is present during each shift"
"doctor A never works on mondays"
- Decide whether solution exists
- Find any solution
- Find optimal solution
Solutions
3 broad categories
- Logic-based
- Arithmetic-based
- Local Search
\varphi
\sum
\nabla
Logic-based
- Decision problems
- Discrete variables
- Disjunctive constraints
- "Artificial Intelligence"
\forall s \in Shift\colon \exists d \in Doctor \colon Assign(s,d)
Assign(s_1,d_1) \vee Assign(s_1,d_2) \vee \ldots \vee Assign(s_1,d_n)
Assign(s_m,d_1) \vee Assign(s_m,d_2) \vee \ldots \vee Assign(s_m,d_n)
\ldots
High level:
Low level:
\varphi
SAT solving
- Back-end technology
- Chip verification, cryptography
- MiniSat, Glucose, Lingeling
x_{11} \vee x_{12} \vee \ldots \vee x_{1n}
\ldots
x_{m1} \vee x_{m2} \vee \ldots \vee x_{mn}
\varphi
Constraint programming
- Language "intuitive for programmers"
- Planning, scheduling
- Chuffed, Gecode, ILOG (IBM), Google Optimization Tools
forall(i in 1..nbshifts)(
sum(j in 1..nbdoctors)(x[i,j]) >= 1
)
\varphi
SMT solving
- Unknown / infinite domains
- Theorem proving, program verification, chip verification
- Z3 (Microsoft), CVC (Intel)
\forall s\colon Assign(s,SomeDoctorFor(s))
\varphi
Answer set programming
- Rule-like, originating from Logic Programming
- Strong recursion support
- SModels, DLV, Clingo
1 \leq \lbrace assign(X,1..n) \rbrace :- ~shift(X)
\varphi
Arithmetic-based
- Optimization
- Numeric variables
- Arithmetic constraints
- "Operations Research"
\forall s \in Shift\colon \exists d \in Doctor \colon Assign(s,d)
\sum_i x_{1i} \geq 1
\ldots
High level:
Low level:
\sum_i x_{mi} \geq 1
\sum
\sum_{k,i} c_{i}x_{ki}
With objective function:
- Floating point variables
- (Linear) relaxation
- Routing, scheduling, production planning
- Cplex (IBM), GuRoBi, Coin-OR, Google Optimization Tools
\sum_i x_{1i} \geq 1
\ldots
Low level:
\sum_i x_{mi} \geq 1
\sum
\sum_{k,i} c_{i}x_{ki}
With objective function:
Mixed integer programming
- Non-linear programming
- Quadratic programming
- Fractional programming
- Geometric programming
- Convex programming
- Semidefinite programming
- ...
\sum
In:
- simple solution
- (extended) objective function
- solution "transformations"
Return: best solution encountered
Local search
\nabla
During: stochastically transform solution into "neighbor" solution
Local search
\nabla
Analogy: hill climbing
- Large problems
- Much hand-work
- designing transformations
- writing custom search algorithm
- No optimality guarantee
- LocalSolver, Tabu search, Simulated annealing
How about IDP?
- Logic-based
- constraint programming + answer set programming
- Rich high-level language
- Implements the knowledge base paradigm
- separate knowledge from task
- solve multiple problems with 1 specification
- E.g., give explanation for empty solution set
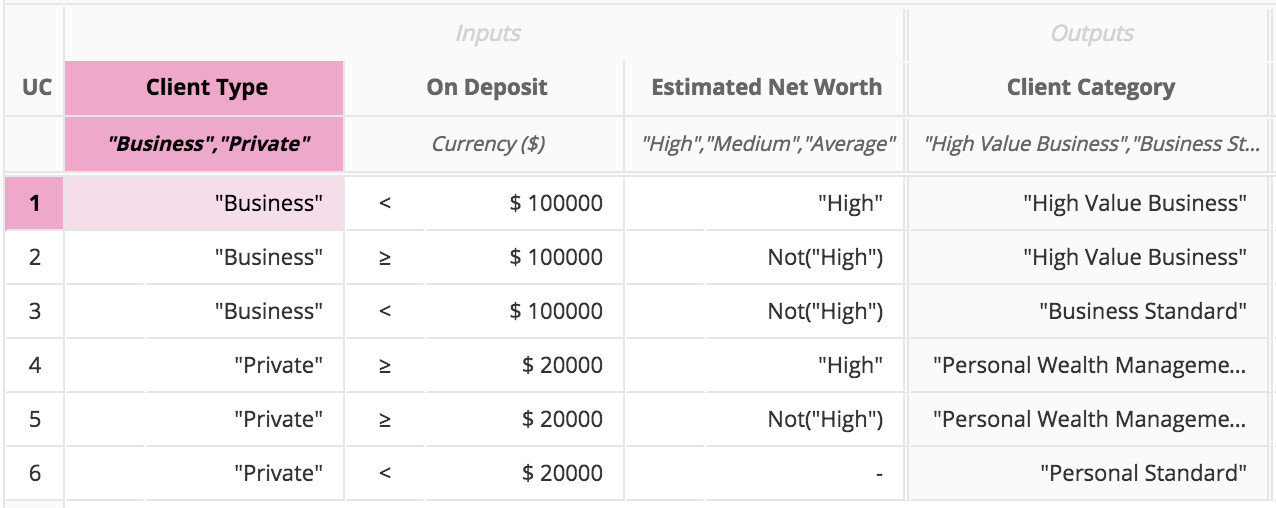
How about DMN?
- Not quite a "reasoning engine"
- inherent workflow: input -> output
- cfr. hamburger problem
- Similar: rule-based systems
- business rule management systems
Thanks for your attention!
Questions?
Solving Technologies
By Jo Devriendt
