The Fractal Flame
Beauty out of Chaos
Johan Karlsson
- Software developer
- I've been coding since the 90's
- JavaScript and Web since 2013
- Patterns, algorithms, animations, fractals
- Dwitter
- Shadertoy
- CodePen
Creative Coding
- Creating freely
- No requirements
- Expression
- Instant feedback
- Generative / algorithmic art
Why?
- Math and algorithms instead
of textboxes over data - Exploring
- The human machine cooperation
- Being surprised
- Relaxing
Mandelbrot Set
{\displaystyle f_{c}(z)=z^{2}+c}
A Fractal
- Math...
- Self-similar
- Benoît Mandelbrot
beautiful, damn hard, increasingly useful. That's fractals.
- Benoît Mandelbrot
Julia Set
Koch Curve
A Fractal Flame
Affine Transformation
f(x, y) = (ax + by + c, dx + ey + f)
(1x + 0y + 0, 0x + 1y + 0) = (x, y)
(1x + 0y + 1, 0x + 1y + 1) = (x + 1, y + 1)
Affine Transform
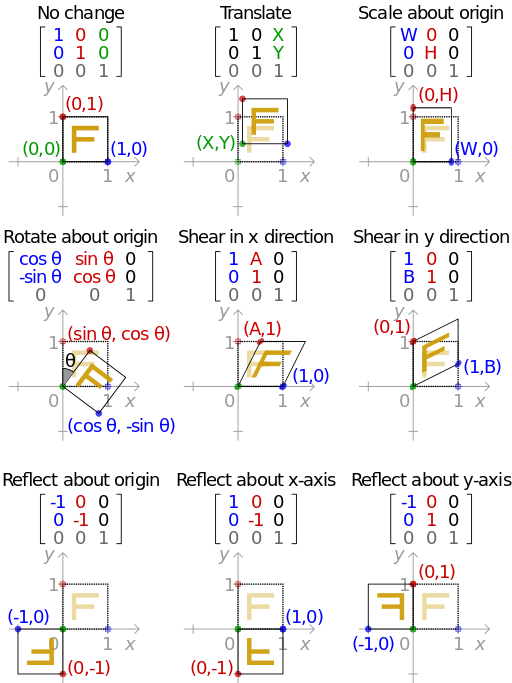
(Wikipedia) "2D affine transformation matrix" by Cmglee - Own work. Licensed under CC BY-SA 3.0 via Commons
IFS - Iterated Function System
- A type of fractal
- Several transformations
- The Chaos Game algorithm
is a common way to compute
(draw) an IFS fractal
The fractal is made up of the union of several copies of itself, each copy being transformed by a function (hence "function system"). - Wikipedia
Sierpinski Triangle - IFS
HSL (HSB)
The Chaos Game
- Create n affine transformations, f1-fn
- Pick a random point (x, y)
-
Loop:
- Apply a random affine transformation to get a new point: (xk+1, yk+1) = fr(xk, yk)
- Plot the new point
Barnsley
Fern
A probability is assigned
to each transformation
Remember
f(x, y) = (ax + by + c, dx + ey + f)
Random IFS
Randomized:
- Number of transformations
- Each coefficient in each transformation
- The color of each transformation
The Fractal Flame
-
Scott Draves
-
Based on the Chaos Game plus:
-
In addition to affine transformations you choose a non-linear function
-
Each affine transformation gets a color associated
-
Using log-density display - a histogram is updated instead of plotting directly
-
Non-linear functions
Swirl
V_3(x, y) = x\sin(r^2) - y\cos(r^2), x\cos(r^2) + y\sin(r^2)
r = \sqrt {x^2 + y^2}
V_{42}(x, y) = (\frac{\sin x}{\cos y},\tan y)
Tangent
V_{27}(x, y) = \frac{2}{(r + 1)}(x, y)
Eyefish
The Fractal Flame Algorithm
-
User picks a non-linear function
-
Create n affine transformations, f1-fn
-
Create empty histogram h[width][height]
- Pick a random point (x, y)
The Fractal Flame Algorithm (cont.)
-
Loop (millions of iterations)
- Apply a random affine transformation OR non-linear function to get a new point: (xk+1, yk+1) = fr(xk, yk)
-
Update histogram color and frequency h[x][y]
h[x][y][color] = (h[x][y][color] + colorr) / 2
h[x][y][frequency]++
-
Draw histogram
-
h[x][y][color]
alpha = log(h[x][y][frequency]) / log(frequencymax)
-
Demo
More info
- The Coding Train by Dan Shiffman
- Coding Math by Keith Peters (bit101)
- Bullet Three
References
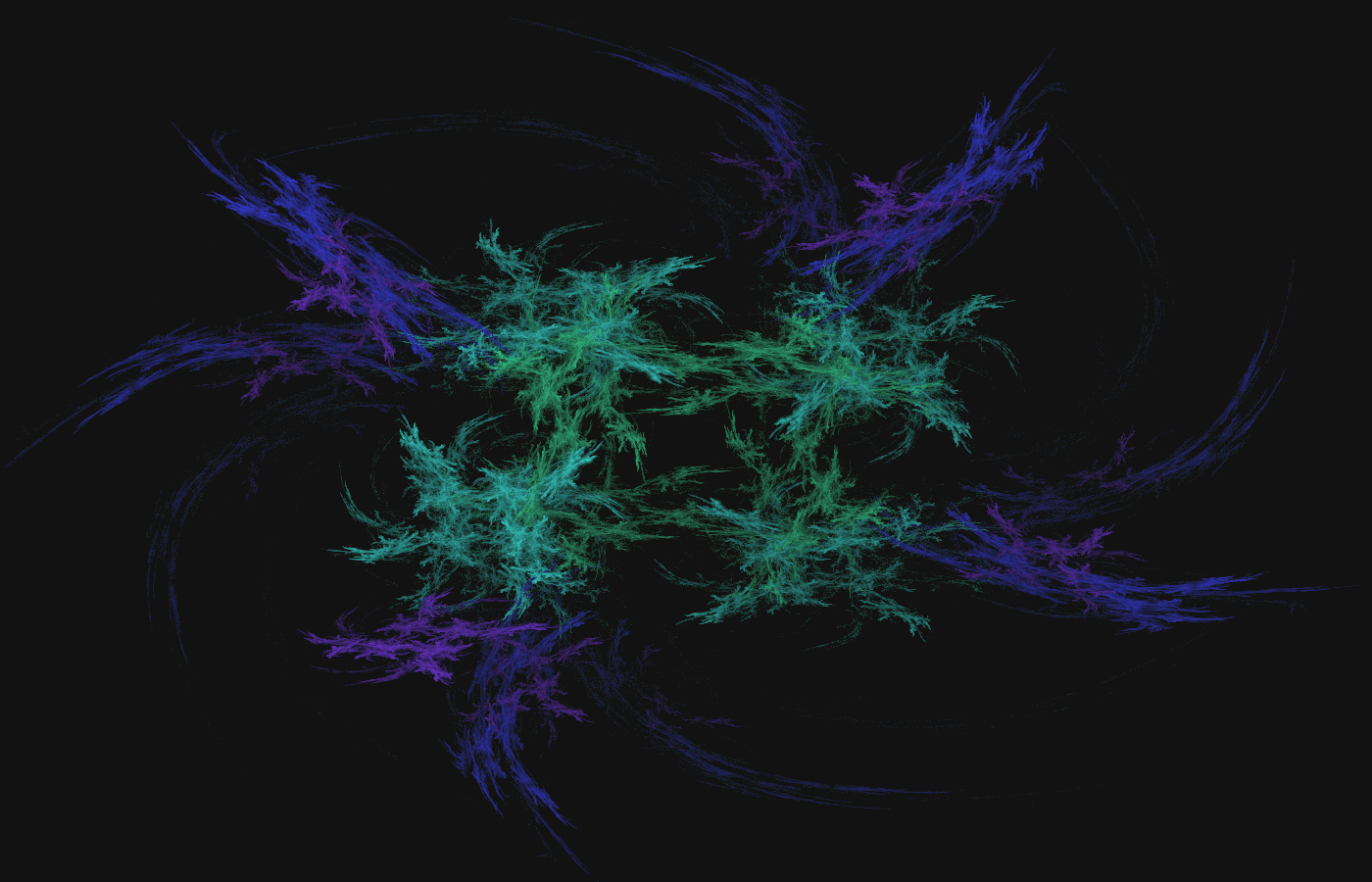
The Fractal Flame
By Johan Karlsson
