ETH Zürich, Combinatorics meeting
Joost Jorritsma,
joint with Tim Hulshof and Júlia Komjáthy
University of Technology Eindhoven
Normally, I'd talk about...
Random Graphs (Probability Theory) with
-
Temporal Structure
Preferential Attachment Graphs -
Spatial Structures
Geometric Inhomogeneous Random Graph -
Stochastic Processes on random graphs
e.g. Random Walk/Epidemic Models - Theoretical focus, not directly applicable
Júlia Komjáthy, Tim Hulshof
https://arxiv.org/abs/2005.06880
...is about...
- Theoretical modeling of epidemics similar to COVID-19
- Qualitative comparisons
- Effect of:
- network topology
- space/geometry
- interventions
- temporary immunity
...is not about...
- Predictions/data oriented modeling for COVID-19
- Quantitative analysis
This talk...
Compartmental model
Two phases:
- Subcritical: \(R_0=\beta/\gamma\le1\):
epidemic vanishes -
Supercritical: \(R_0>1\):
exponential incline, long survival - Stationary solution
Susceptible
Infected
Temporary Immune
\(\beta I(t)/N\)
\(\gamma\)
\(\eta\)
Mean-field model:
- \(S(t), I(t), T(t)\in\mathbb{R}\)
- well-mixed population
Susceptible
Infected
Infect neighbor w.p. \(\beta\)
w.p. \(\gamma\)
w.p. \(\eta\)
Network approach
Temporary Immune
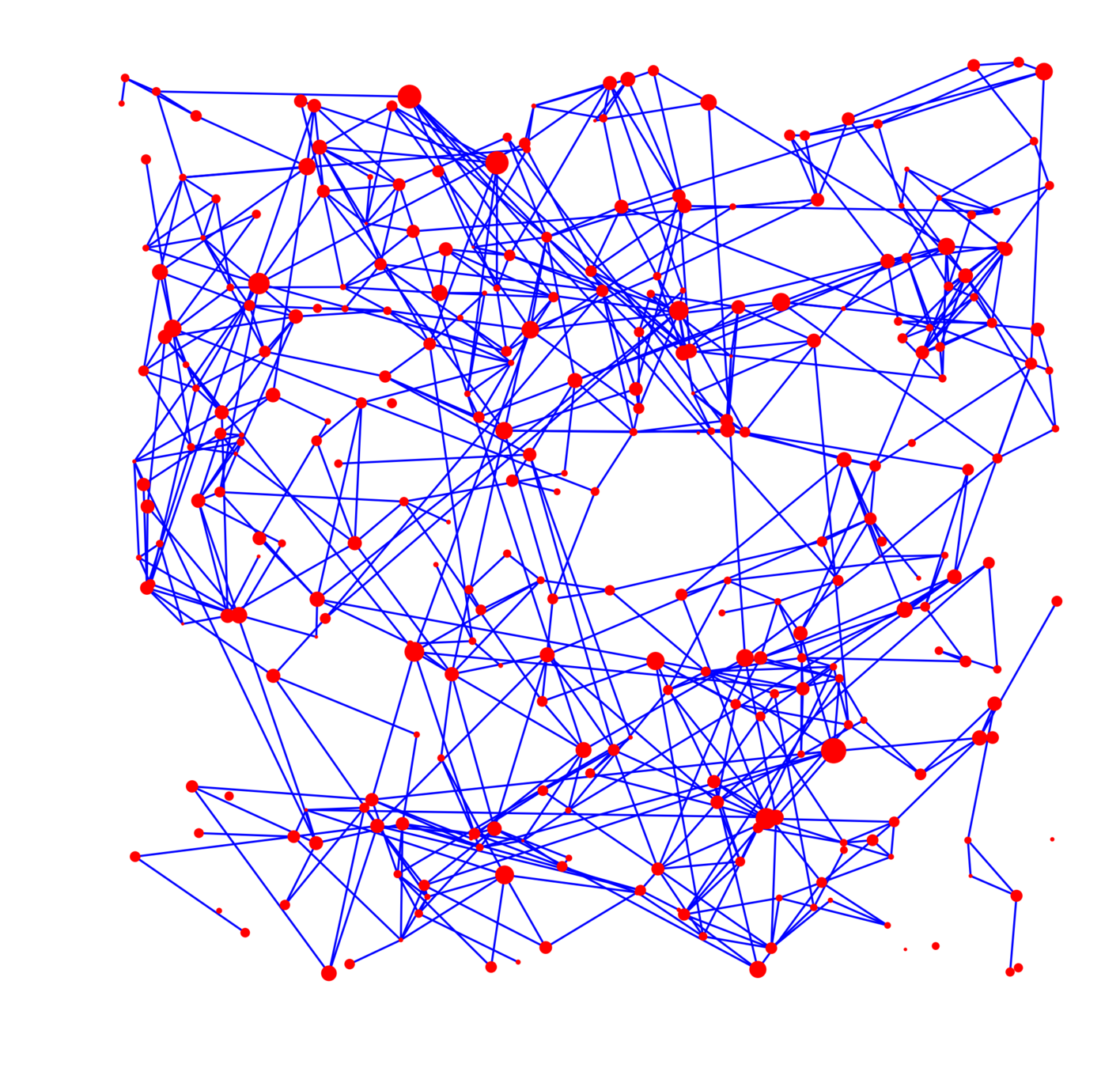
Choice of network
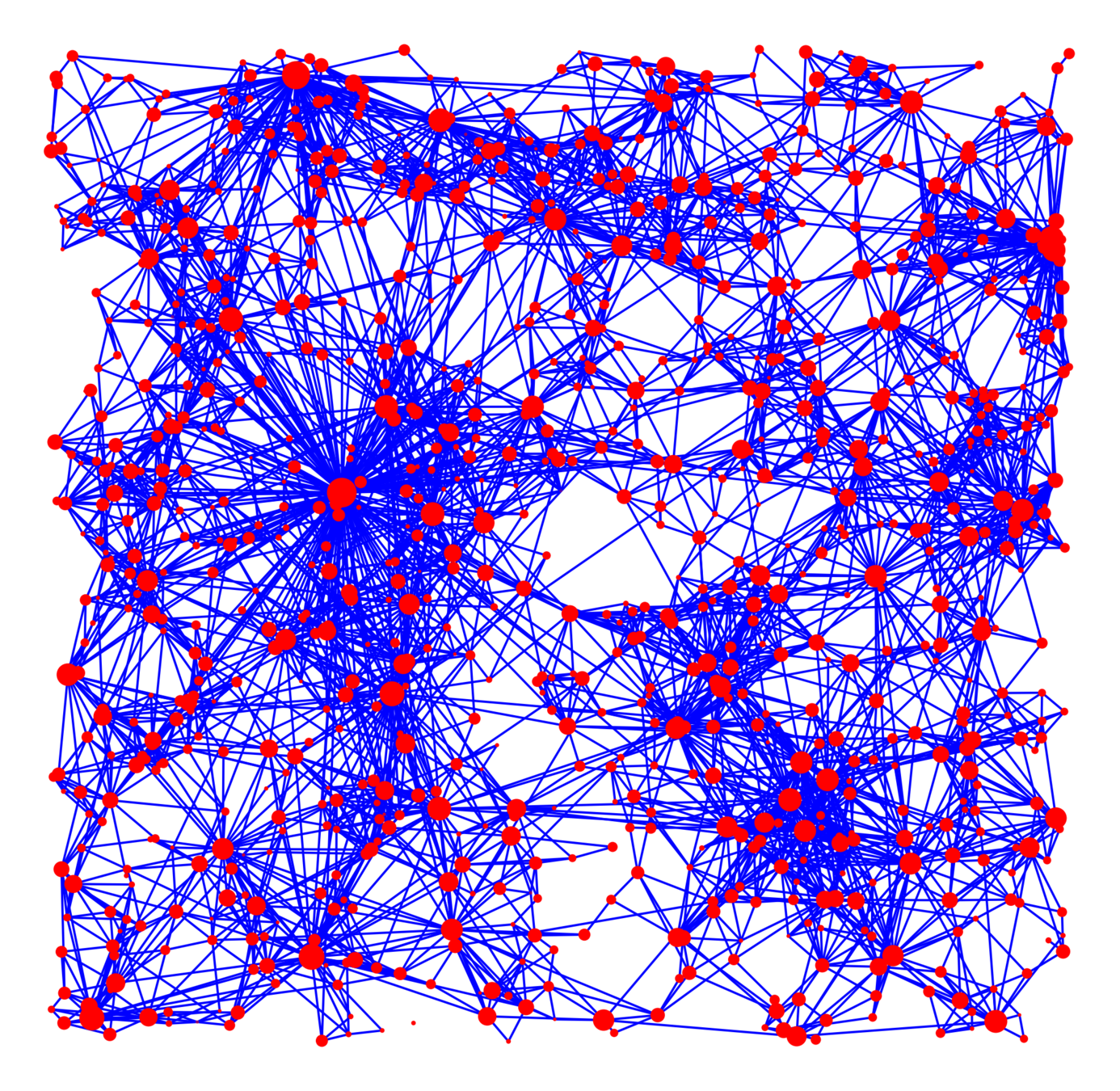
Geometric Inhomogeneous Random Graph
- Spatially induced clustering,
heavy-tailed degree distribution.
- \(n\) nodes uniformly in \([0,\sqrt{n}]^{2}\).
- Power-law weight/fitness for vertices:
- Condition on weights & locations (\(\alpha>1\)):
\mathbb{P}(x\leftrightarrow y \mid W_x, W_y) \asymp \min\Big\{1, c \left(\frac{W_xW_y}{\|x-y\|^2}\right)^\alpha\Big\}.
\mathbb{P}(W\ge w) \asymp w^{-(\tau-1)}, \qquad \tau>2.
- Smaller \(\tau\): more variability in weights/degrees.
- Smaller \(\alpha\): more long-range connections.
Temporary immunity:
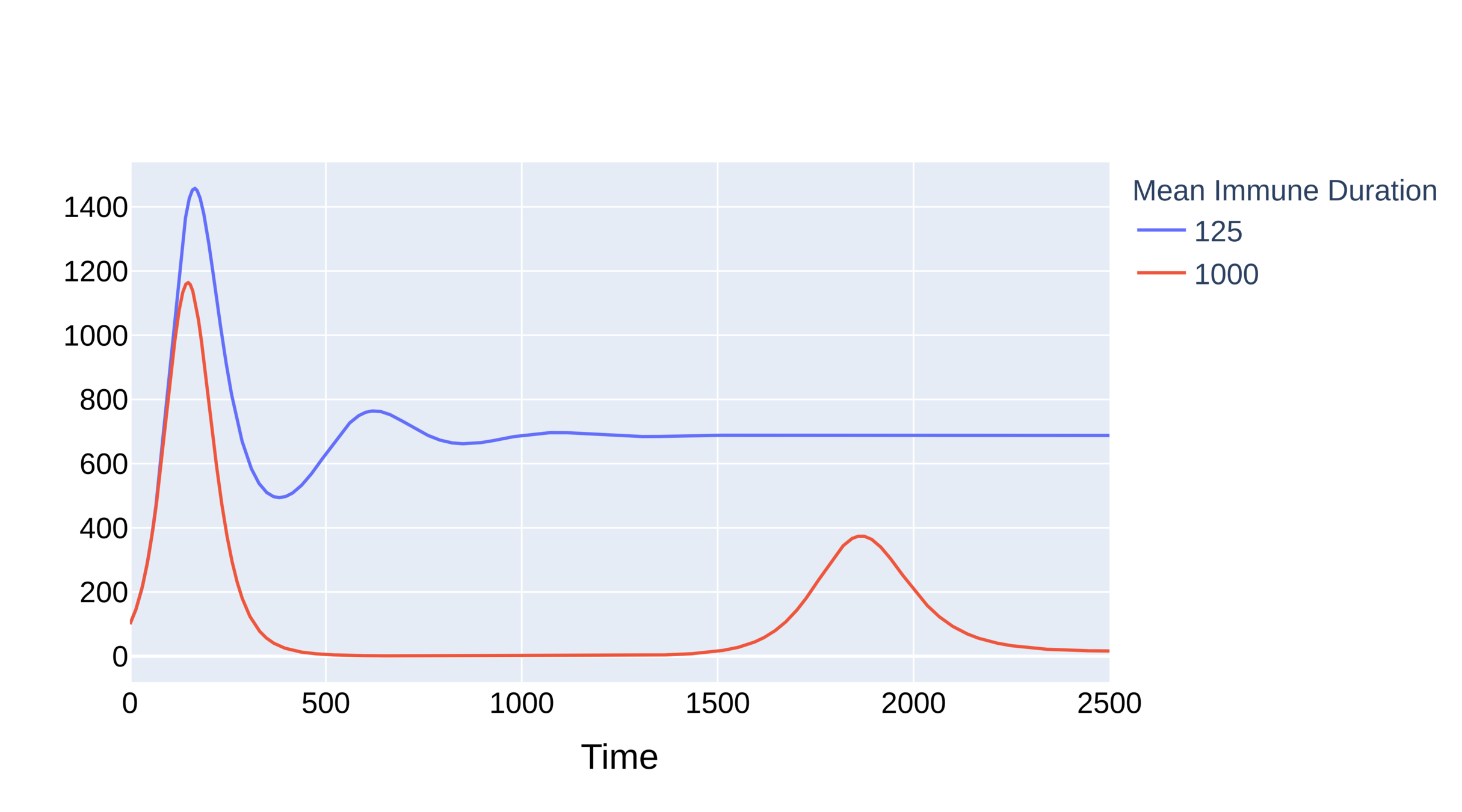
Two types of supercriticality
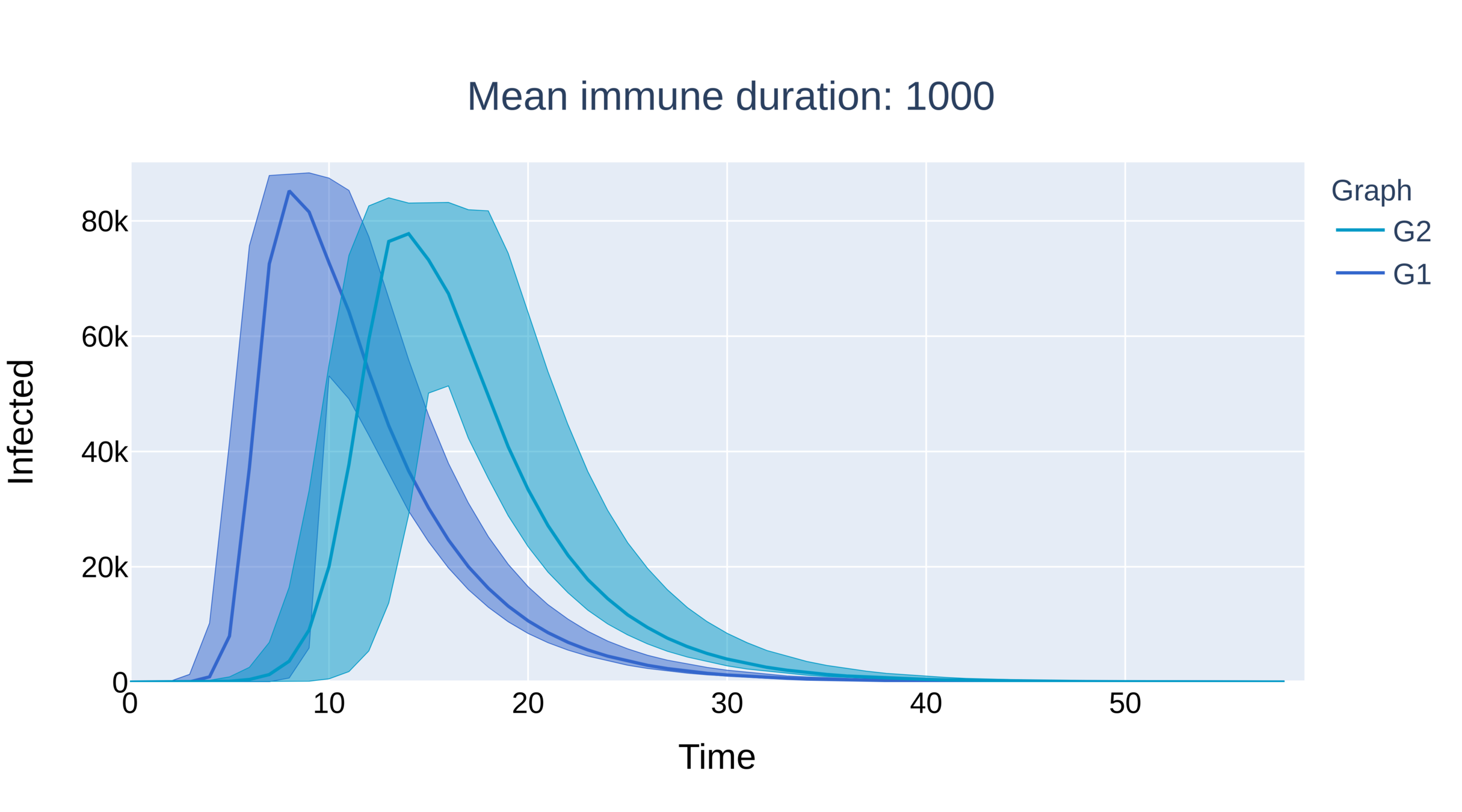
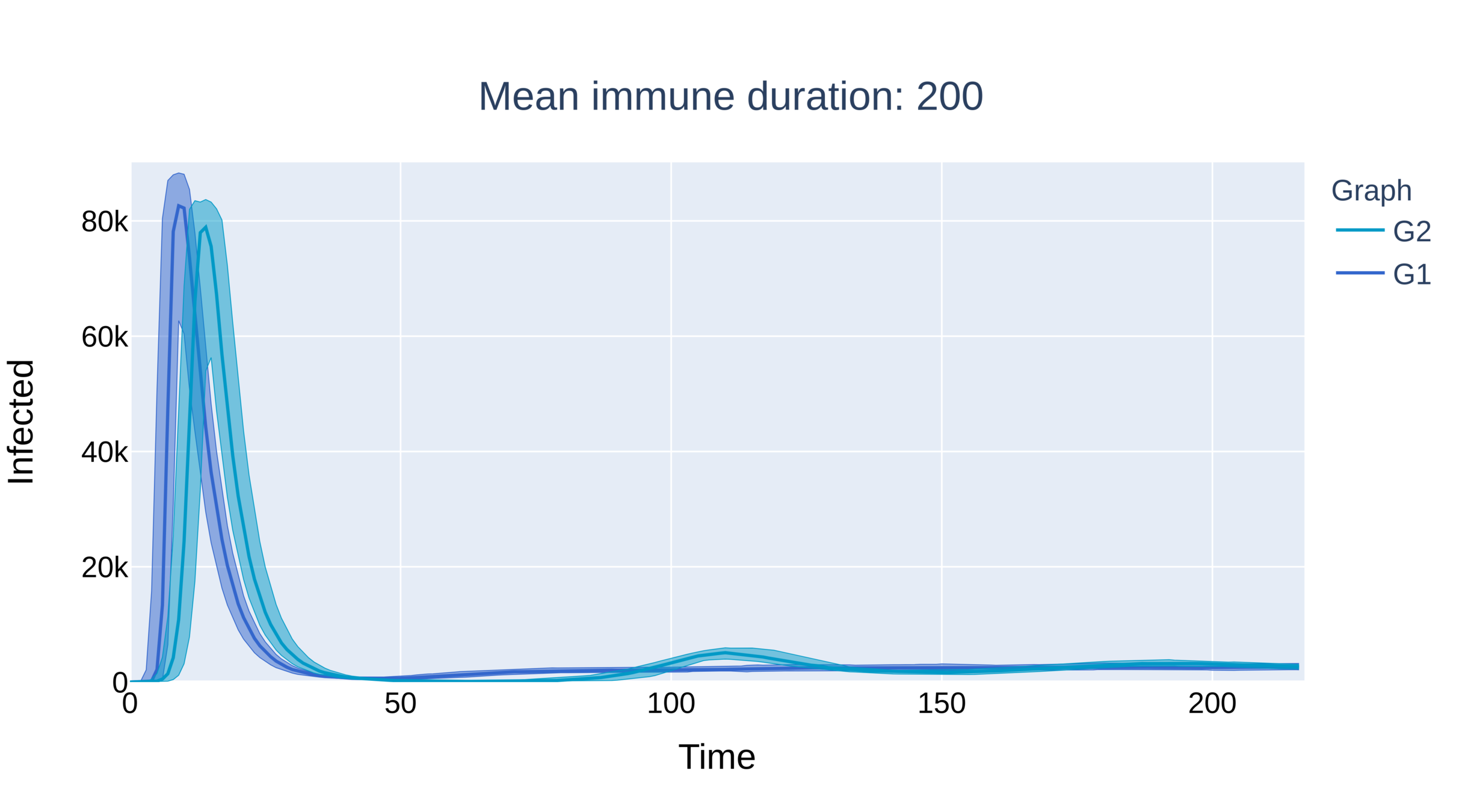
Parameters:
\(\beta=.225\),
\(\gamma=.2\)
mean deg. \(\approx 9\)
\(\tau>3\)
\(\tau\in(2,3)\)
\(\eta=0.001\)
\(\eta=0.005\)
\(=\eta\)
Modeling interventions: remove edges
- Remove edges before start epidemic
- Resulting epidemic still supercritical
- "Rule" per intervention strategy:
- Social dist.: Random
- No travel: Long edges
- No hubs: Removing edges from large-degree nodes
- Match intervention parameters s.t. average degree after intervention is comparable (approx. 60% edges remain)
No interv.
Social dist.
No travel
No hubs
No travel works best for the first peak
Graph with power-law exponent \(\tau>3\)
- Travel restrictions bring down first peak, but elongate the outbreak
- Absence of long-range edges: Average graph distance increases from logarithmic to polynomial in network size
- First peak insensitive for immunity
- Similar figure for graph G1 (\(\tau\in(2,3)\))
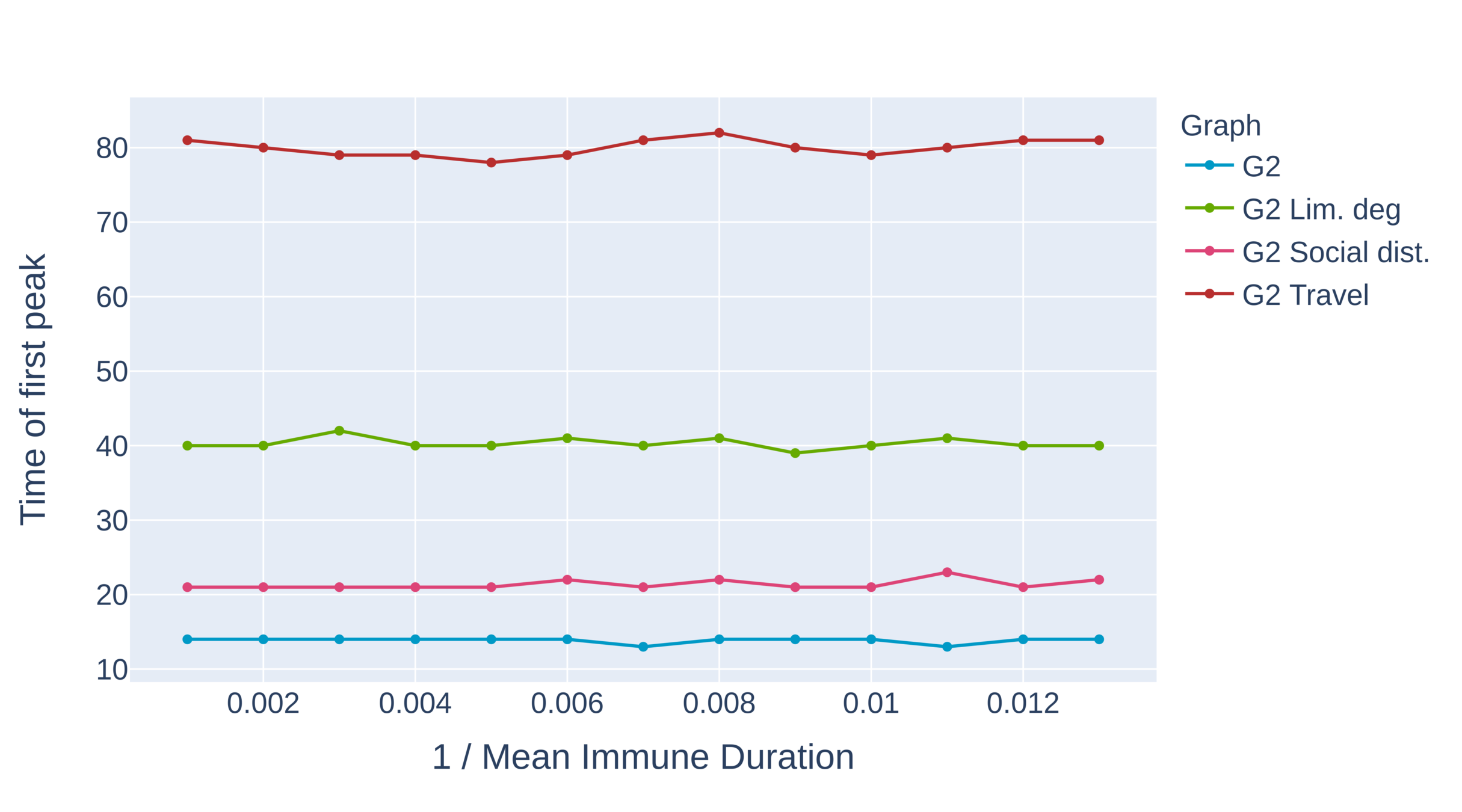
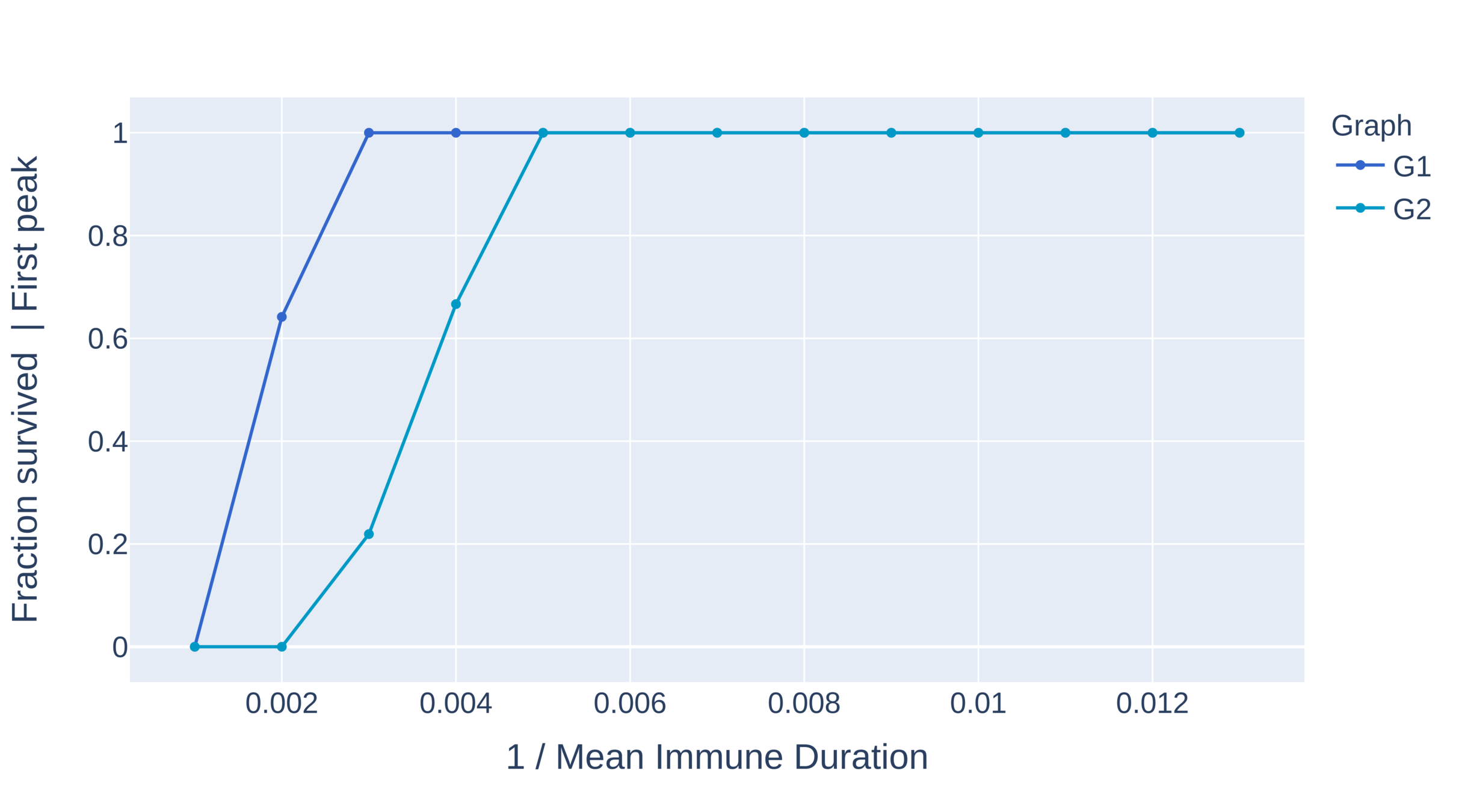
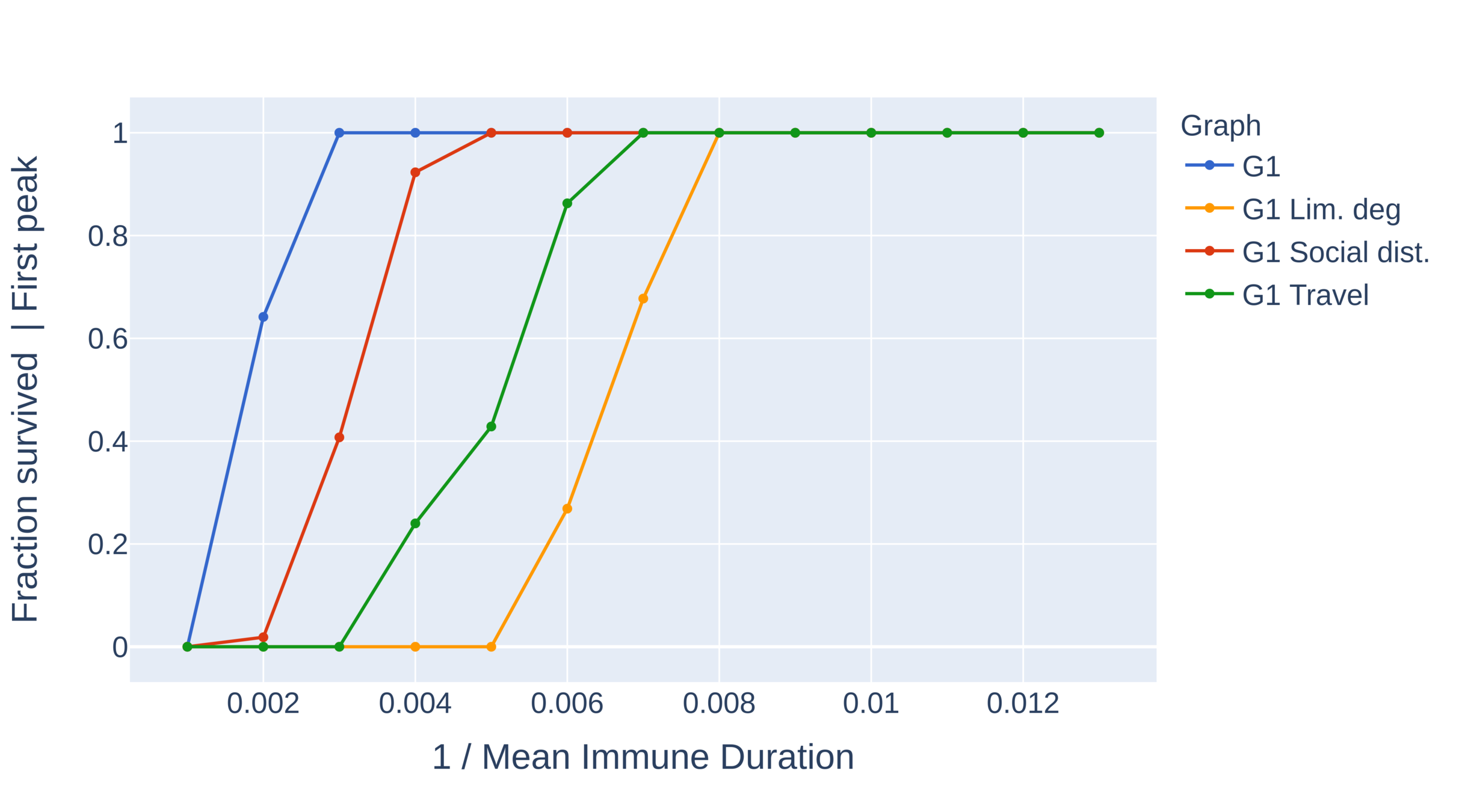
Critical immune duration decreases under interventions (I)
Graph with power-law exponent \(\tau>3\)
- Critical immunity length is shortest under limitation of degree and travel restrictions.
- Absence of hubs: larger oscillations
- First peak for travel restrictions is as high as second peak under degree limitation
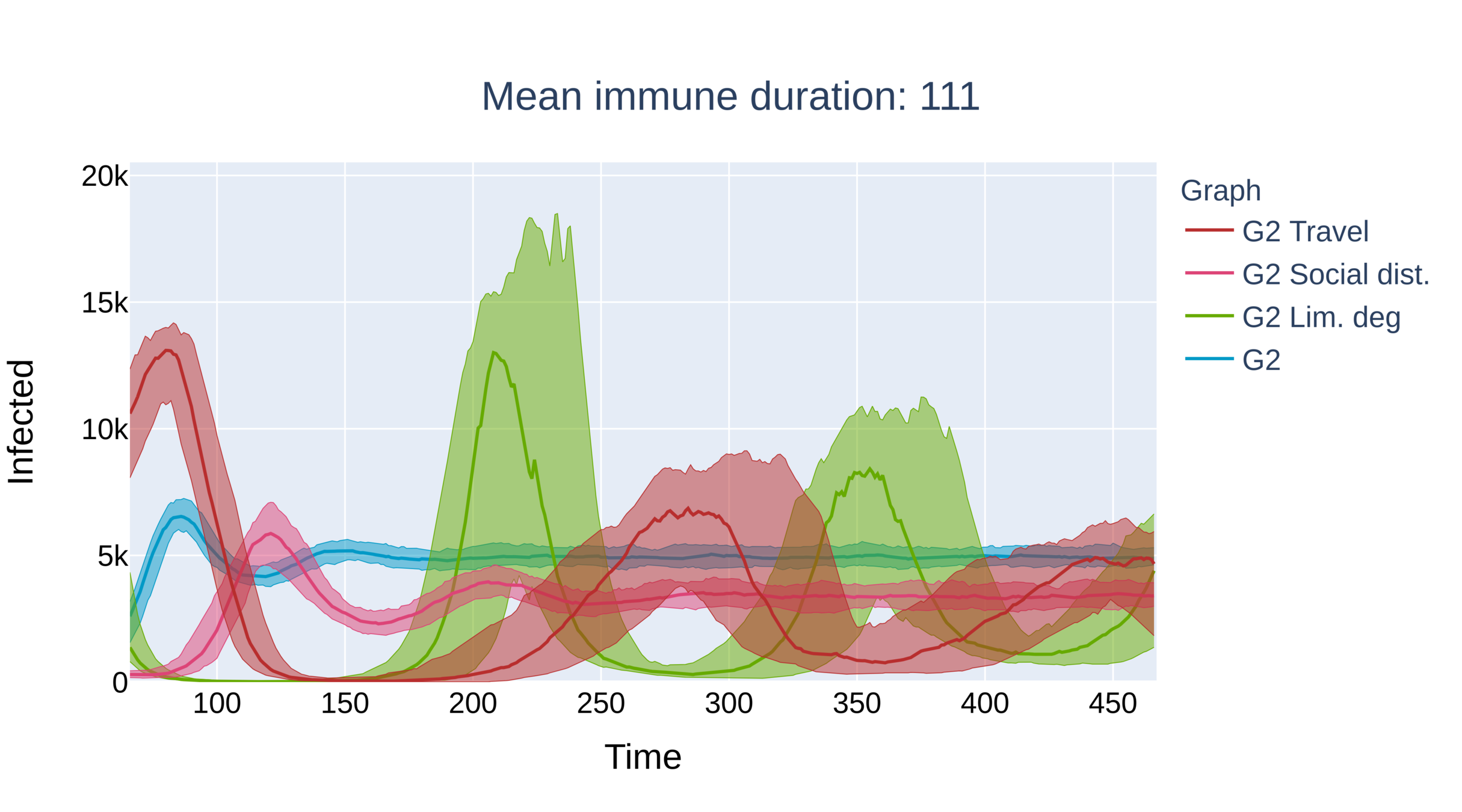
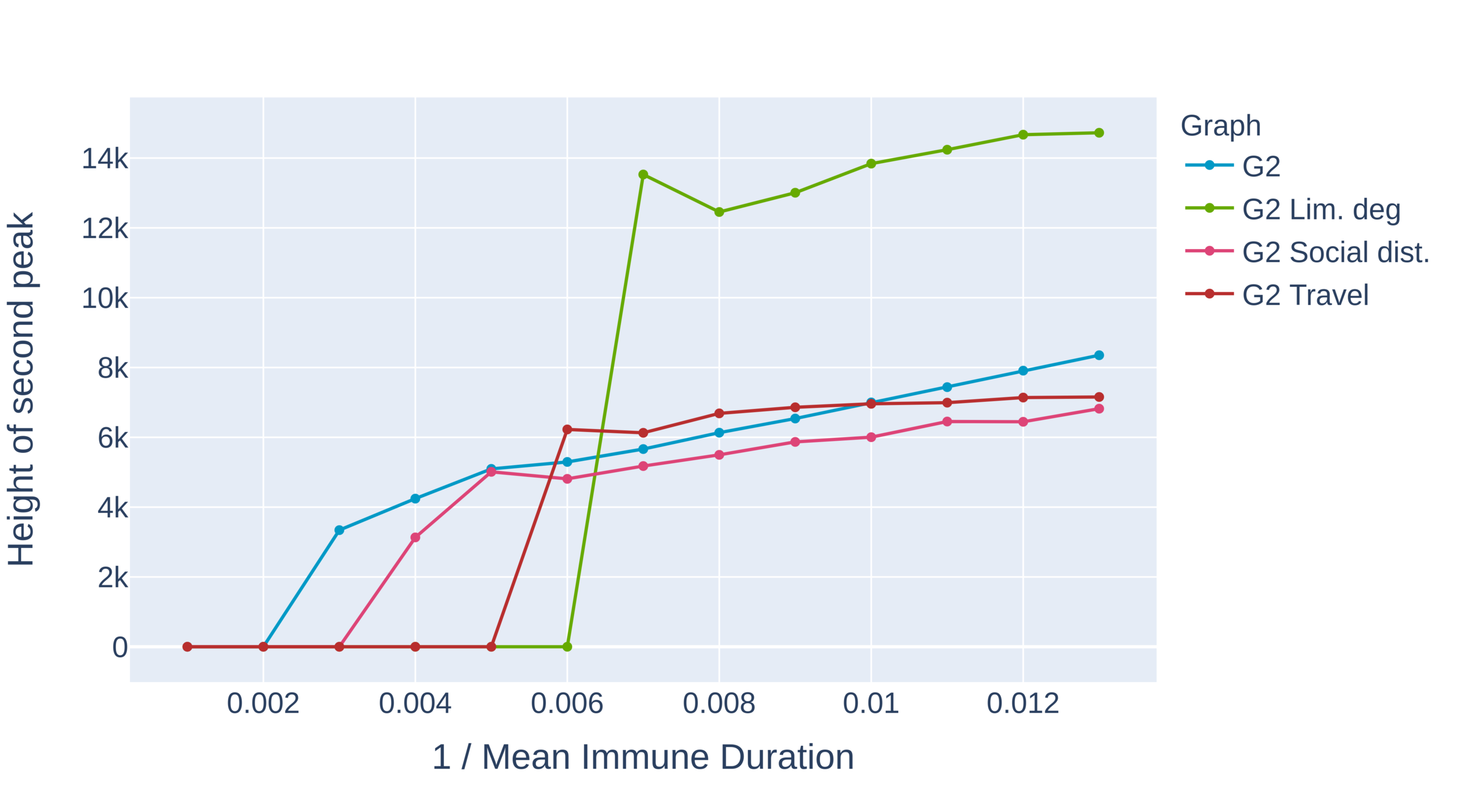
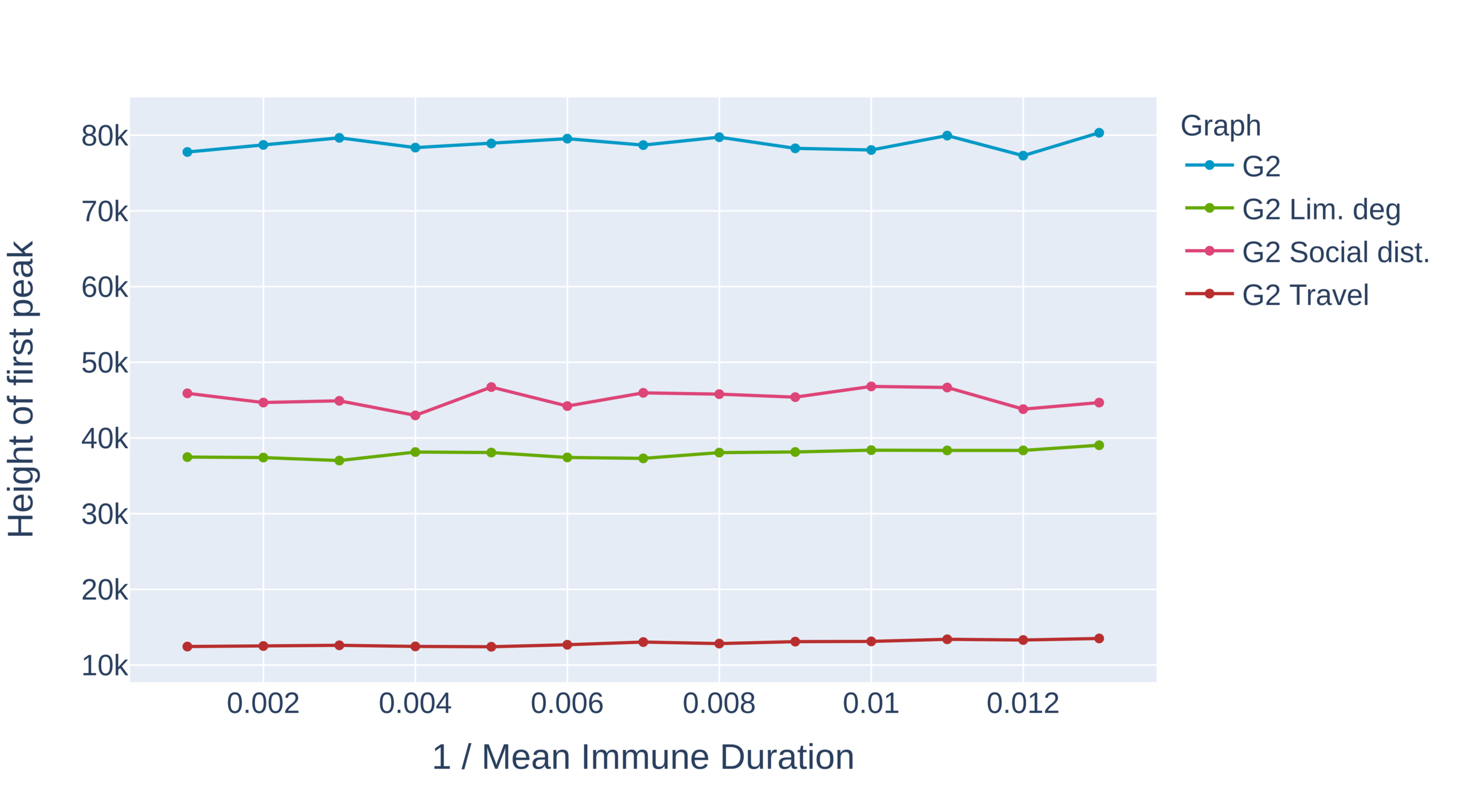
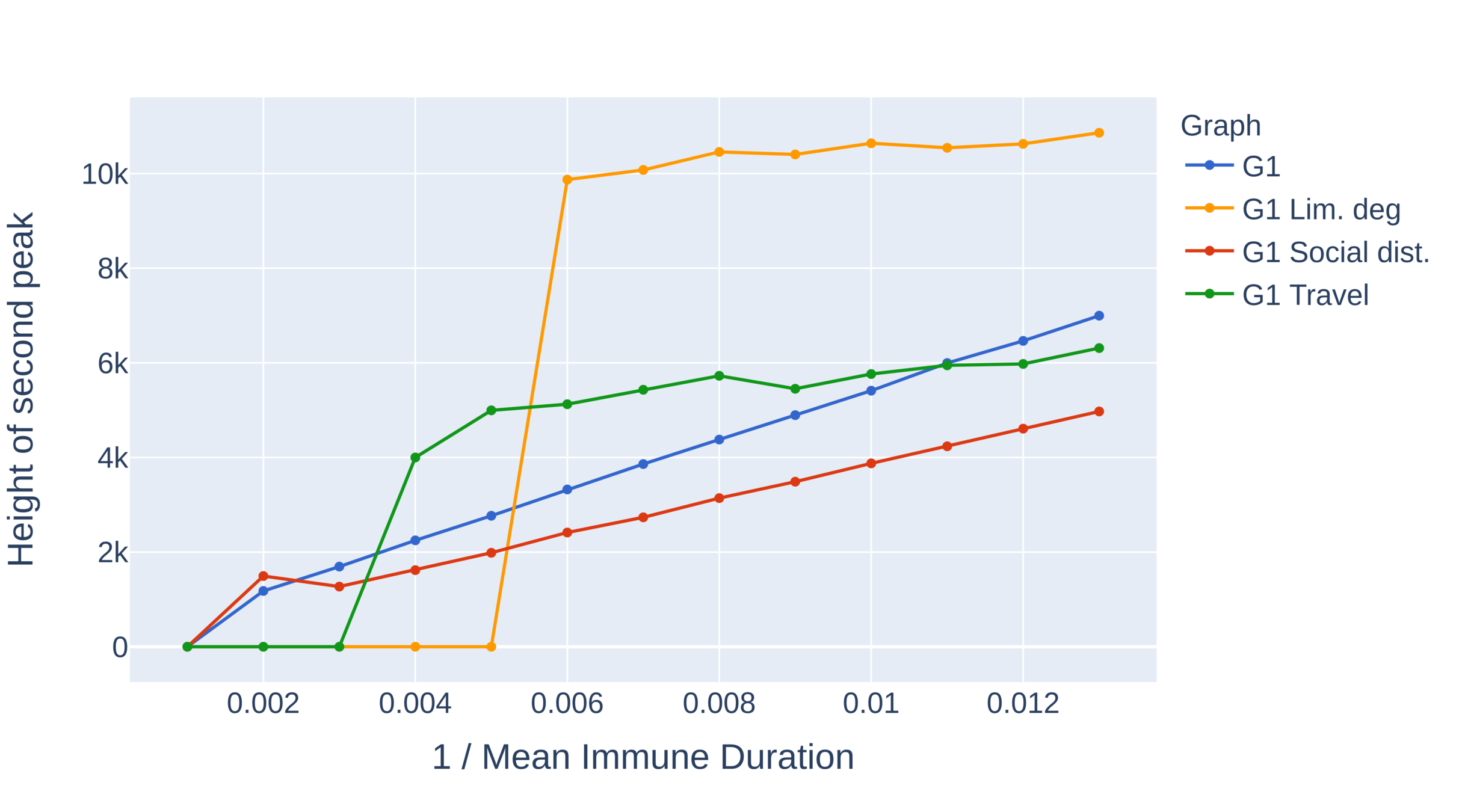
Critical immune duration decreases under interventions (II)
Graph with power-law exponent \(\tau\in(2,3)\)
- Without intervention the system immediately equilibriates.
- Critical immunity length is smallest under limitation of degree, travel restrictions outperform social distancing.
- No oscillations for social distancing. Presence of larger hubs brings the system to equilibrium quicker.
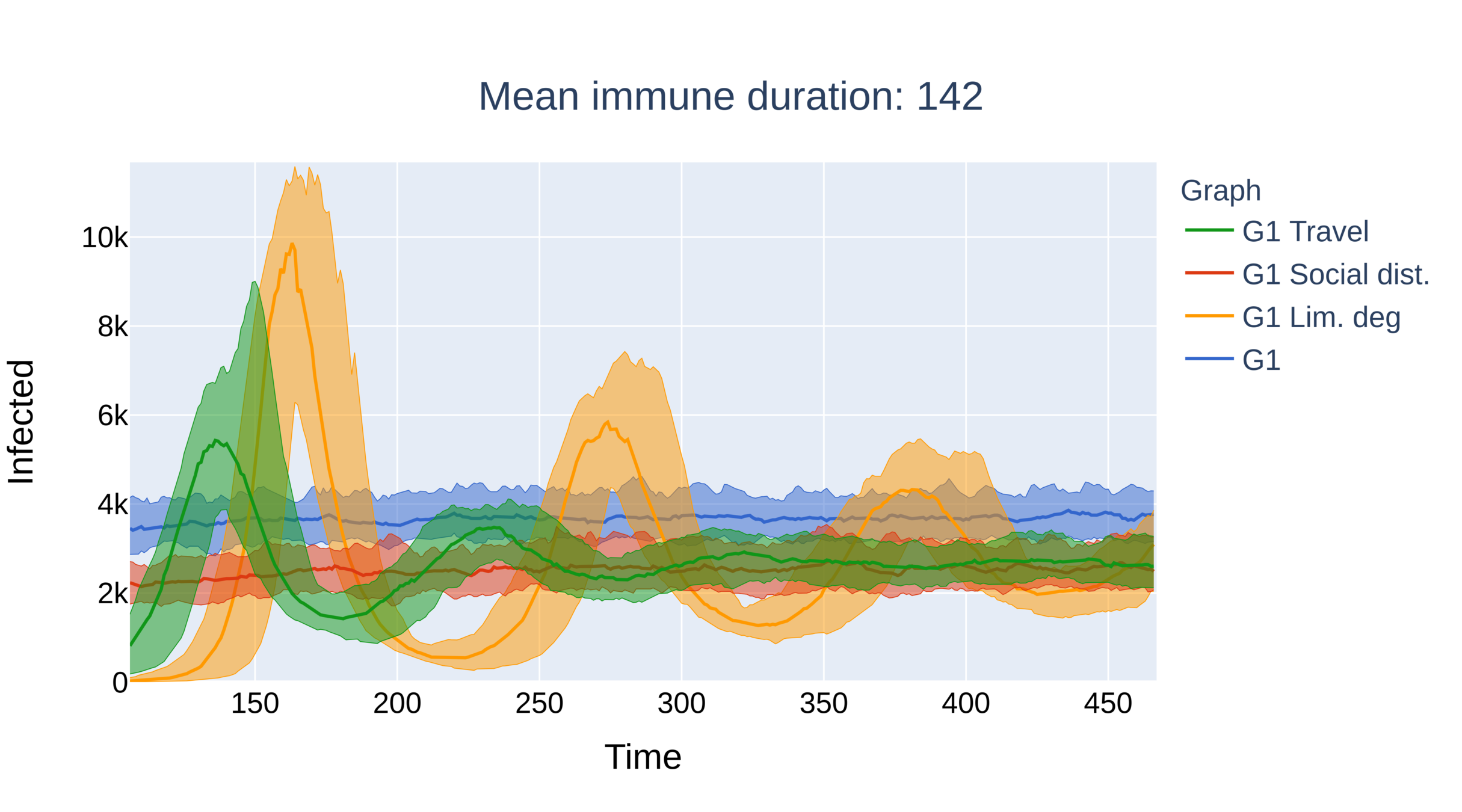
Main conclusions
- Epidemics on networks with underlying geometry show richer behaviour than compartmental models.
- Network topology plays a profound role.
- Networks allow for intuitive modeling of interventions.
- Travel restriction works best but they elongate epidemic.
- Limiting node degree might result in high second peak
Thank you for your attention!
https://arxiv.org/abs/2005.06880
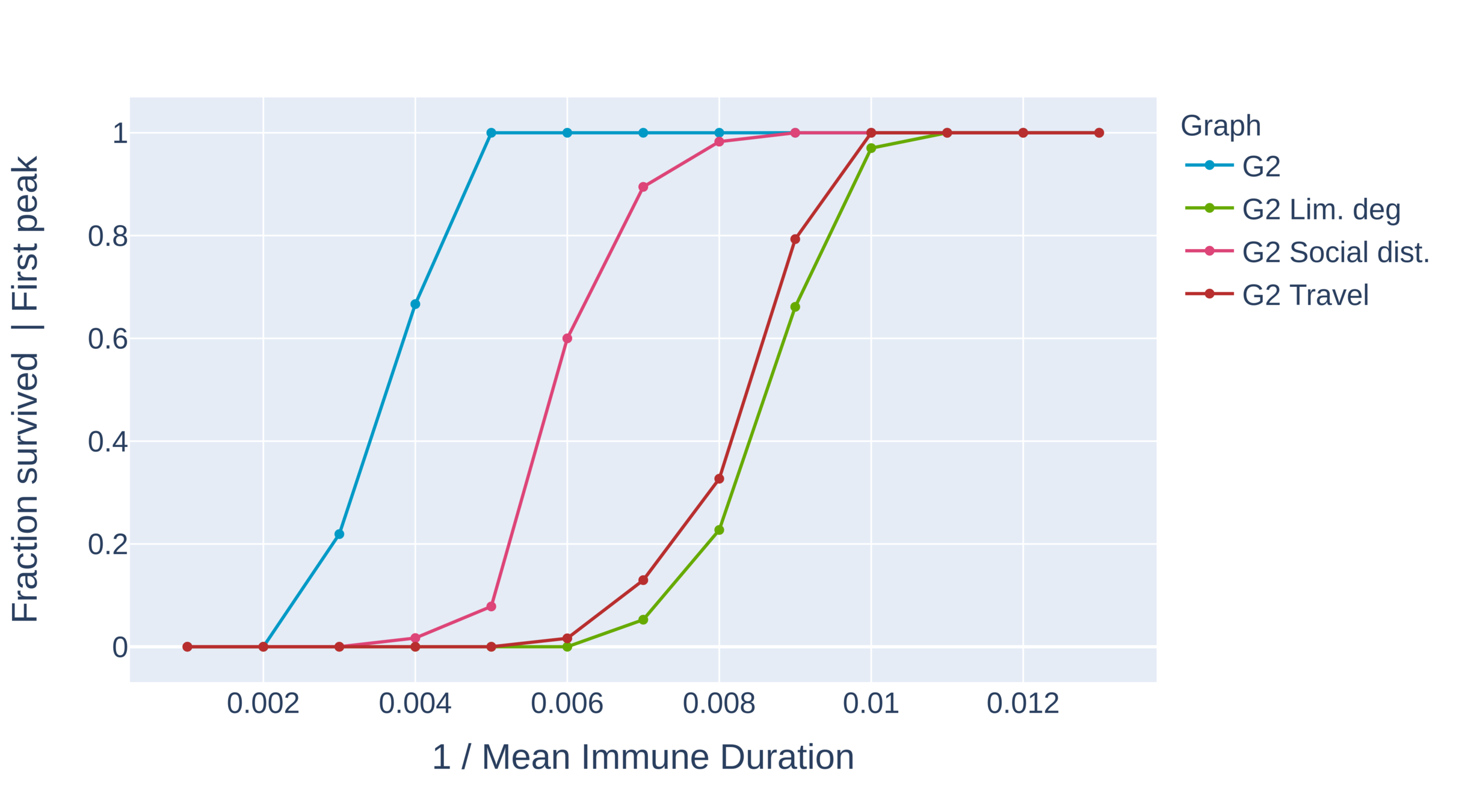
Long survival probability under interventions
Higher degree-spread diminishes amplitude
No travel works well for later peaks
Higher degree-spread diminishes amplitude
No travel works well for later peaks
Higher degree-spread diminishes amplitude
Compartmental model
- Additional states could be added
- "Mean-field" model: everything is averaged out:
individuals are equal, everybody is weakly connected, individuals are "real-valued"
- Only way of modeling interventions:
Set \(\beta:=\beta(t), \gamma:=\gamma(t), N:=N(t)\). - Unclear how and why interventions work
- What is the most effective intervention?
Susceptible
Infected
Recovered
\beta \frac{I(t)S(t)}{N}
\gamma
Network-based approach
Susceptible
Infected
Recovered
Infect neighbor w.p. \(\beta\)
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
Network-based approach
Susceptible
Infected
Recovered
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
- At random (social dist.)
Infect neighbor w.p. \(\beta\)
Network-based approach
Susceptible
Infected
Recovered
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
- At random (social dist.)
- Euclidean length (no travel)
Infect neighbor w.p. \(\beta\)
Network-based approach
Susceptible
Infected
Recovered
Heal w.p. \(\gamma\)
- Contact network as a graph
- Infectious nodes infect neighbors
- Models "coincide" for complete graph and scaling \(\beta\)
- Interventions: remove edges
- At random (social dist.)
- Euclidean length (no travel)
- Degree (limit # contacts)
Infect neighbor w.p. \(\beta\)
ODE approach
Susceptible
Infected
Recovered
Infect neighbor w.p. \(\beta\)
Heal w.p. \(\gamma\)
Susceptible w.p. \(\eta\)
- Immunity unclear for COVID-19
- Natural model for "second" peaks
Network approach
Network topology
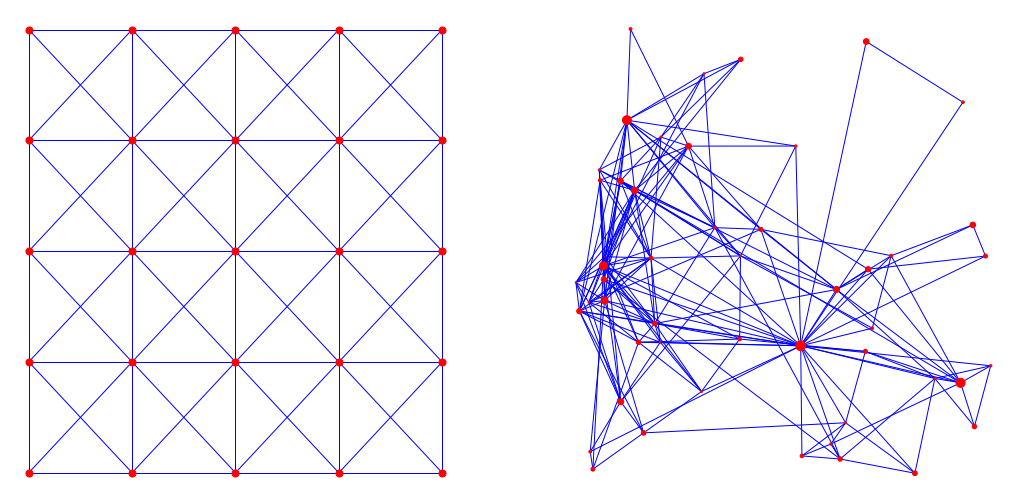
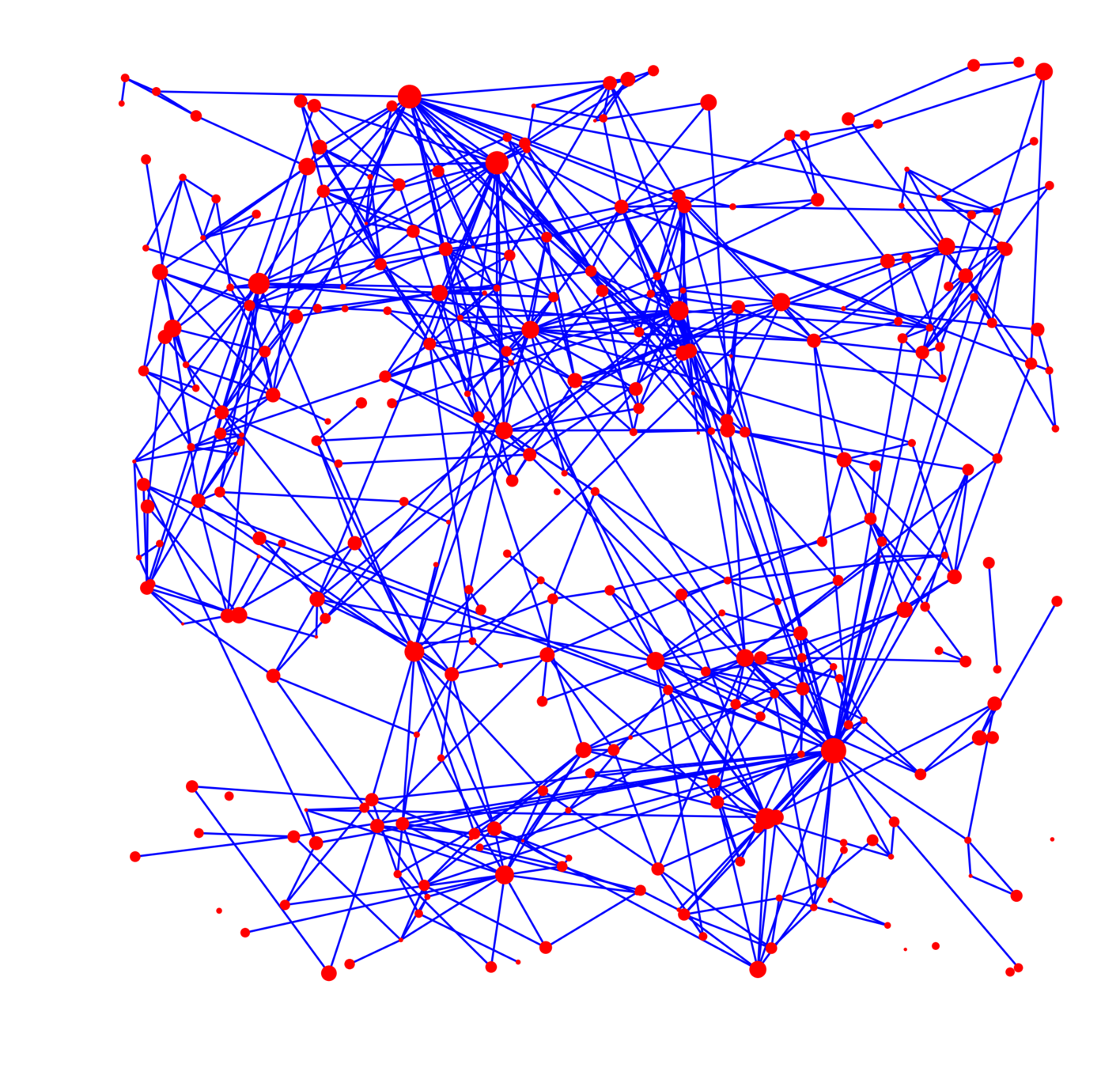
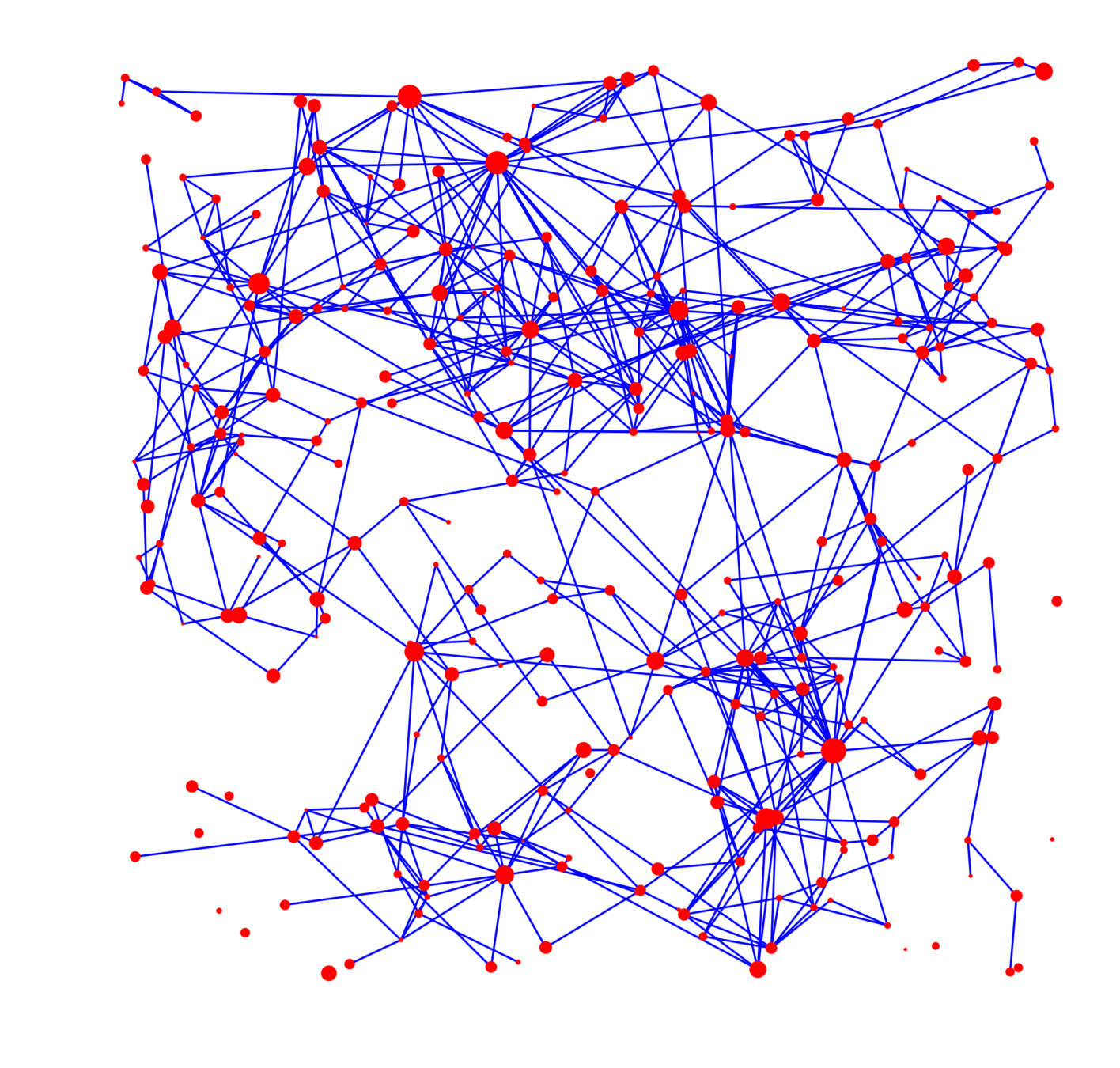
Two graphs with mean degree 8
Network approach
Network topology
Mean degree 8, 160000 nodes
Network approach
Network topology
Two graphs with mean degree 8
Polynomial growth
"Faster" growth
Network approach
Network topology
Desired features
- "close" nodes are
likely to be connected - High variability in degrees
- "Important" nodes are
likely to be connected
Random graph model (\(\alpha>1\)):
p_{ij} \approx c\Big(\frac{W_iW_j}{\|x_i-x_j\|^2}\Big)^\alpha
Results
- Network vs. Compartmental
- New phases
- Oscillations
-
Effect of social dist., no travel, no hubs
- How to compare?
- First peak
- Later peaks
- Probability of survival
Supercritical epidemic dies out in network for \(\eta\) small
Single peak, extinction
large graphs, 100 runs
Survival
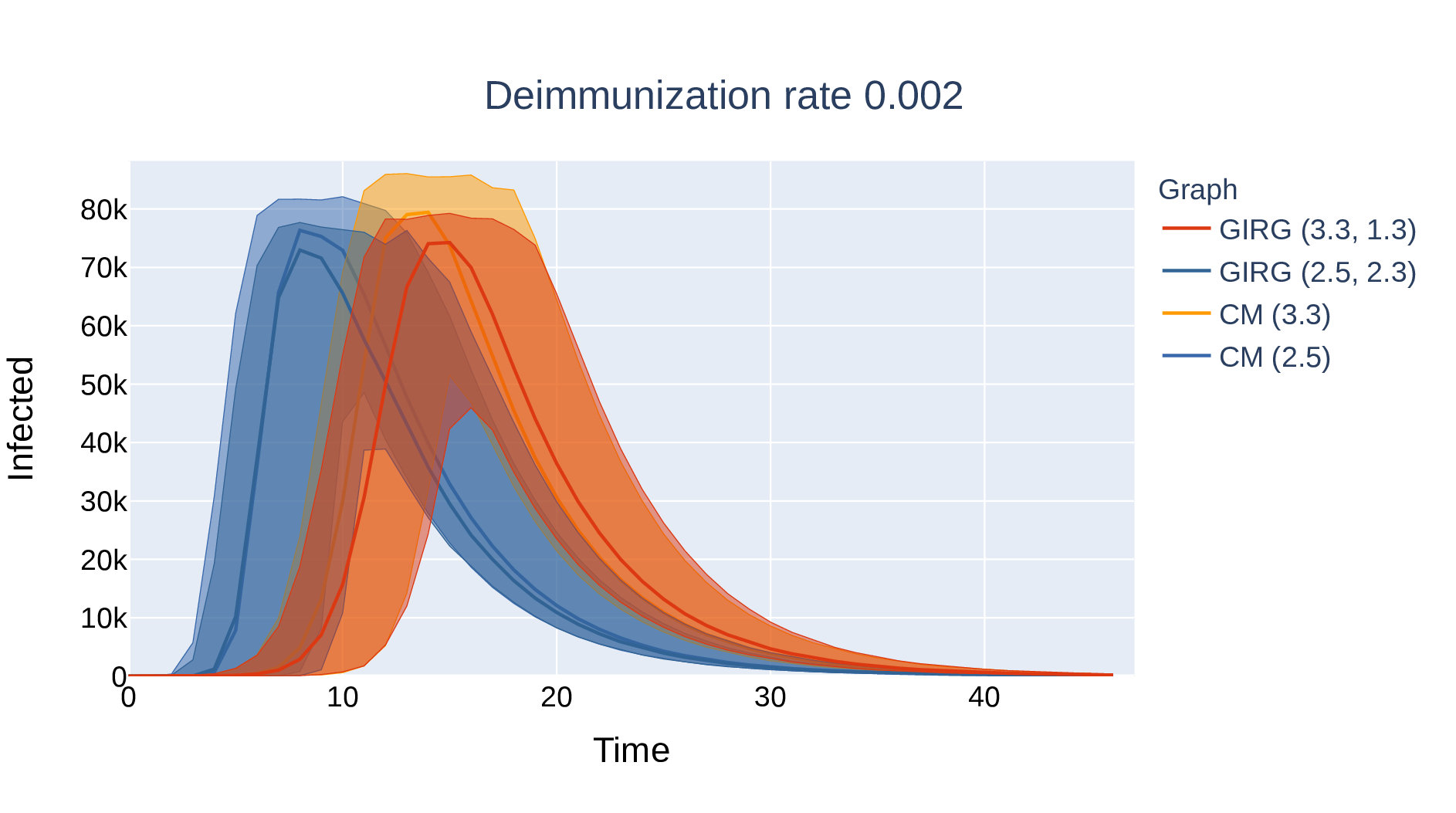
Four networks
Compartmental,
\(\eta\) small and large
Geometry introduces "immunity boundaries", herd immunity
Supercritical epidemic can survive in network for \(\eta\) large
Four networks
Compartmental,
\(\eta\) small and large
Single peak, survival
large graphs, 100 runs
Survival
Supercritical epidemic can survive in network for \(\eta\) large
Oscillations in three networks
Absence of long edges: larger amplitude
Results
-
Network vs. Compartmental
- New phases
- Oscillations
-
Effect of social dist., no travel, no hubs
- How to compare?
- First peak
- Later peaks
- Probability of survival
Combinatorics meeting: Corona Interventions on GIRGs
By joostjor
