SC9 Probability on Graphs & Lattices

Joost Jorritsma

joost.jorritsma@stats.ox.ac.uk

Math,

Music,

Biking

Understanding network models 

Probability, Combinatorics

& Physics, Epidemiology, ...

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

FINAL SIZE
Randomized optimization algorithms
Optimization under chance constraints
Sampling algorithms for explainable AI

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

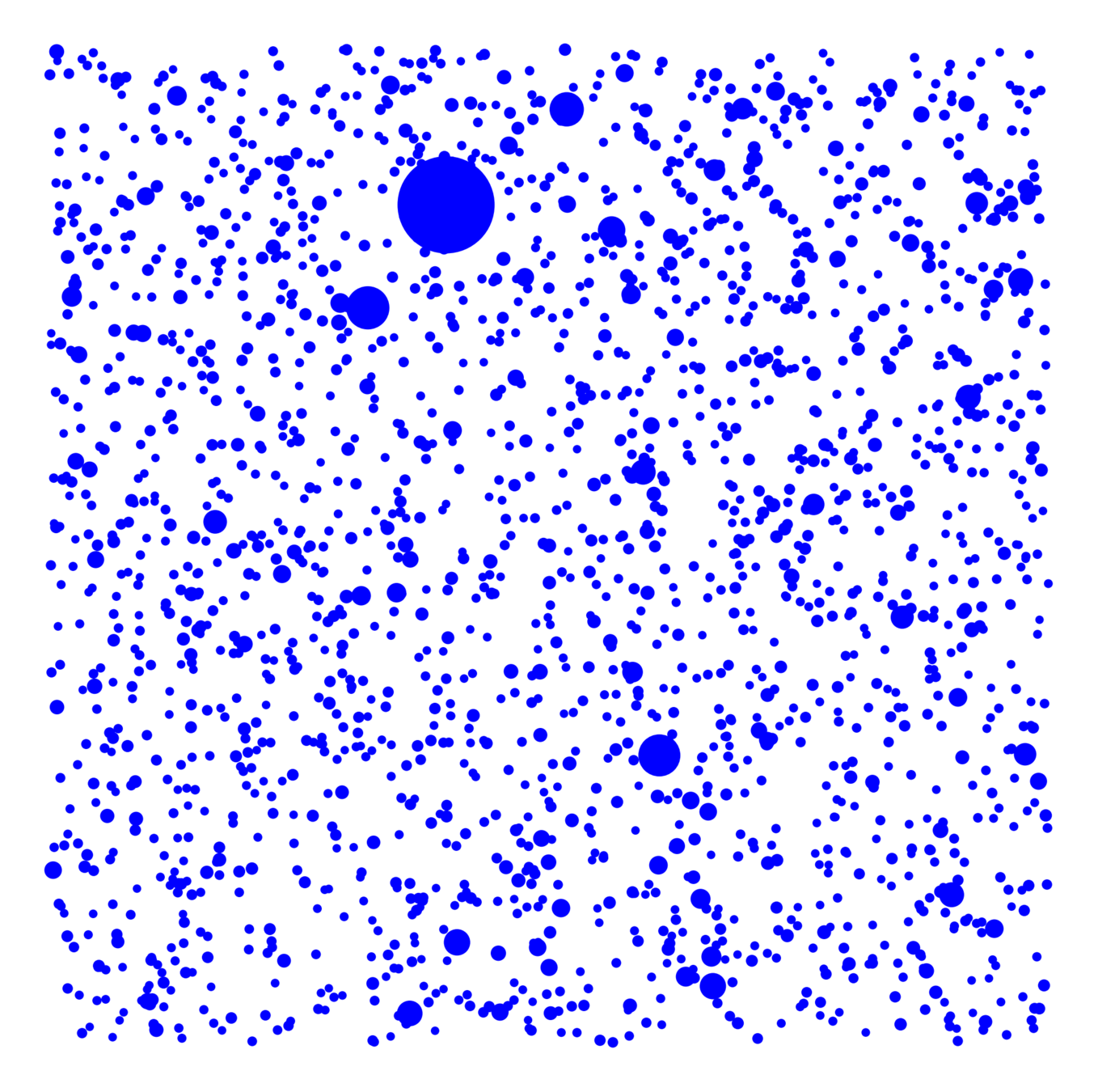
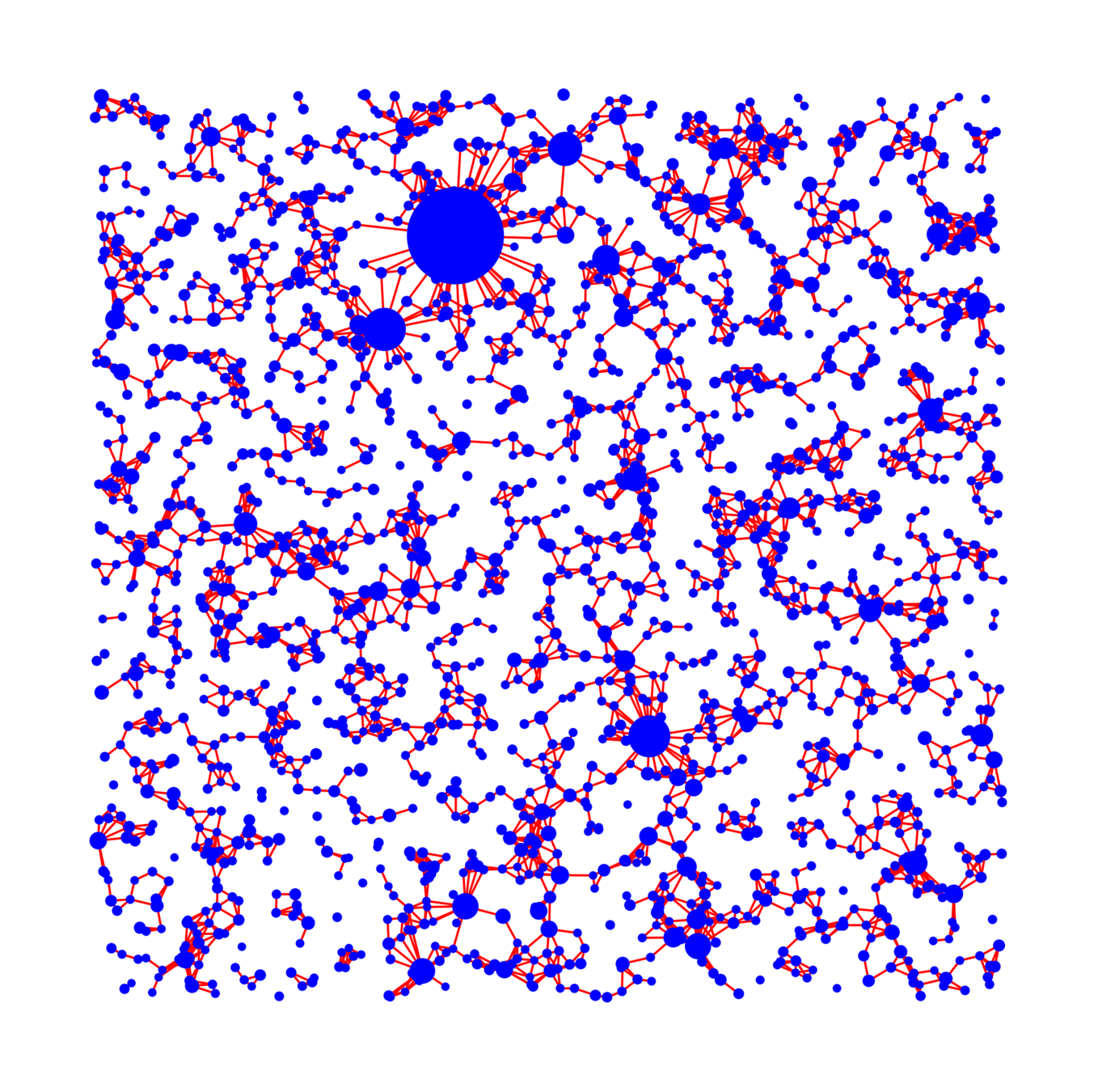
Vertex set

  • Spatial locations
  • Vertex weights

Edge more likely if

  • Spatially nearby,
  • High weight

Spatial random graphs

Percolation: Reed-Frost epidemic

Four parameters: new and classical models

New phenomena

  • Delocalized connected components
  • Double-exponential neighbourhood growth
  • Large outbreaks more likely than small outbreaks

Challenges

  • Geometry:
    • Short/Long edges
  • Presence of hubs

New direction: Scaling limits of trees and random graphs

  • Only vertex weights, no location
  • Edge lengths scale with graph size

Figure by Igor Kortchemski

Setup

  • Include asymmetry in edge probabilities
  • Uncountable and unbounded weights

Goal

References

  1. The Continuum Random Tree; David Aldous; Annals of Probability (1991).
  2. Limits of multiplicative inhomogeneous random graphs and Lévy trees: limit theorems;
    Nicolas Broutin, Thomas Duquesne, Minmin Wang; Probability Theory & Related Fields (2021).
  3. Cluster-size decay in supercritical long-range percolation;
    With Júlia Komjáthy, Dieter Mitsche; Electronic Journal of Probability (2024).
  4. Cluster-size decay in supercritical kernel-based spatial random graphs;
    With Júlia Komjáthy, Dieter Mitsche; Min. revision in Annals of Probability, arXiv: 2303.00712.
  5. Large deviations of the giant in supercritical kernel-based spatial random graphs;
    With Júlia Komjáthy, Dieter Mitsche; Preprint     arXiv: 2404.02984.
  6. Surface order large deviations for Ising, Potts and percolation models;
    Agoston Pisztora; Probability Theory and Related Fields (2024).
     

Department Away Day `24

Joost Jorritsma

Random graph models for real-world networks

Department Away Day `24

Joost Jorritsma

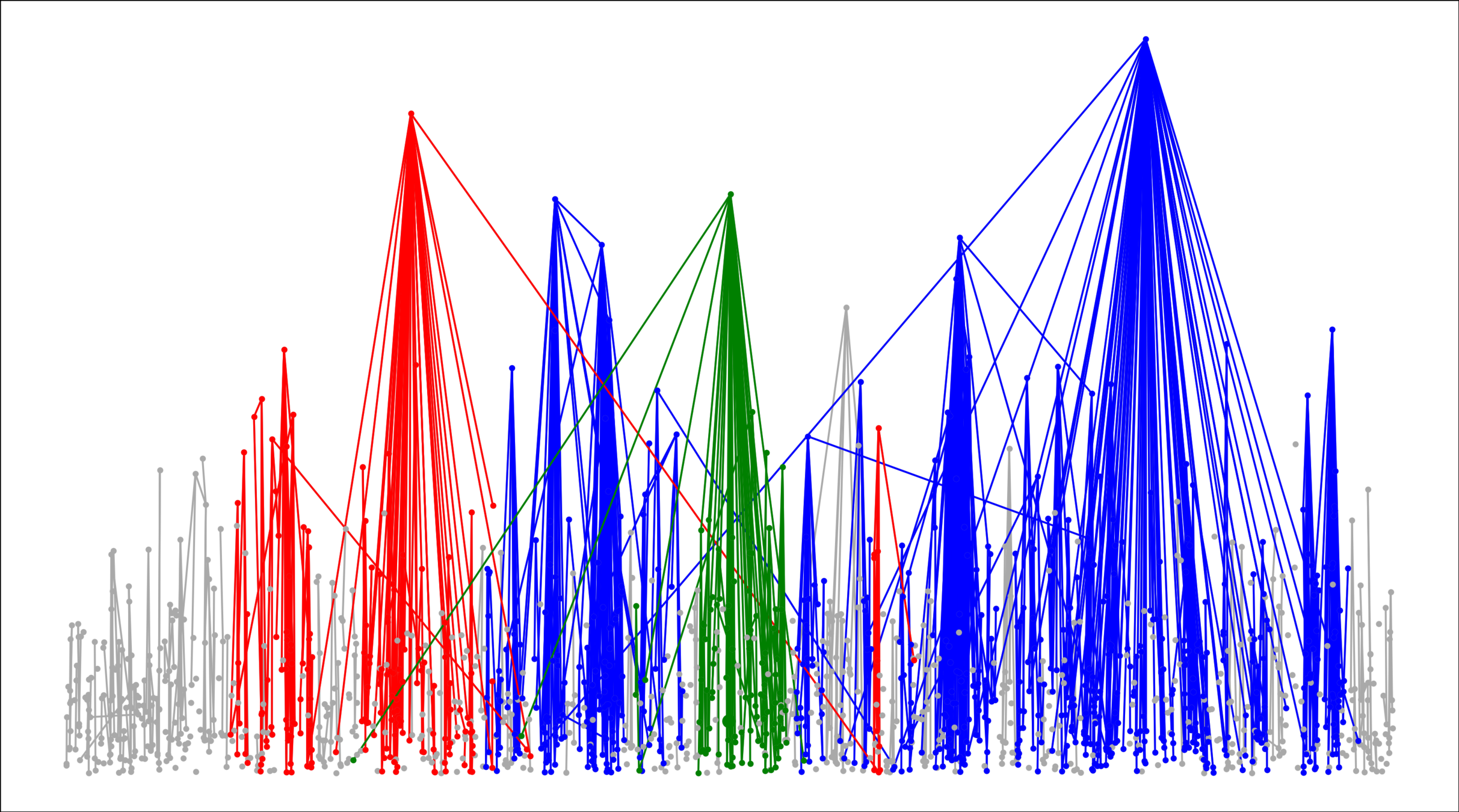
Internet: a growing network of routers and servers

~1969: 2 connected sites

Time

~1989: 0.5 million users

~2023: billions of devices

  • [Faloutsos, Faloutsos & Faloutsos, '99]:
    • Short average distance:
      Quick spread of information

~1999: 248 million users

Distance evolution in a growing network

1999

\(\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4\)

2005

\(\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3\)

2024

\(\mathrm{dist}_{{\color{red}'24}}(u_{'99}, v_{'99}) = 2\)

21 possible networks

Attachment rule:

Prefer connecting to high-degree vertices, \(\tau\): tail of power-law degree distribution

2005

\(\phantom{\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3}\)

Distance evolution

Distance evolution: hydrodynamic limit

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}\longrightarrow 0.$$

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(\phantom{t'=T_t(a):=t\exp\big(\log^a(t)\big)}\) for \(\phantom{a\in[0,1]}\), then

$$ \phantom{\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.}$$

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} \phantom{- (1-a)\frac{4}{|\log(\tau-2)|}}\right|\phantom{\overset{\mathbb{P}}\longrightarrow 0.}$$

  • Dynamics in PAMs.
  • Generalization with edge weights: 
random transmission times
Novelties

  • Fast spreading among influentials;

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\phantom{\overset{\mathbb{P}}\longrightarrow 0.}$$

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume \(\tau<3\).
Let \(t'=T_t(a):=t\exp\big(\log^a(t)\big)\) for \(a\in[0,1]\), then

$$ \phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\phantom{\overset{\mathbb{P}}\longrightarrow 0.}$$

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

FINAL SIZE

Real networks contain many triangles!

Do real networks look like this?

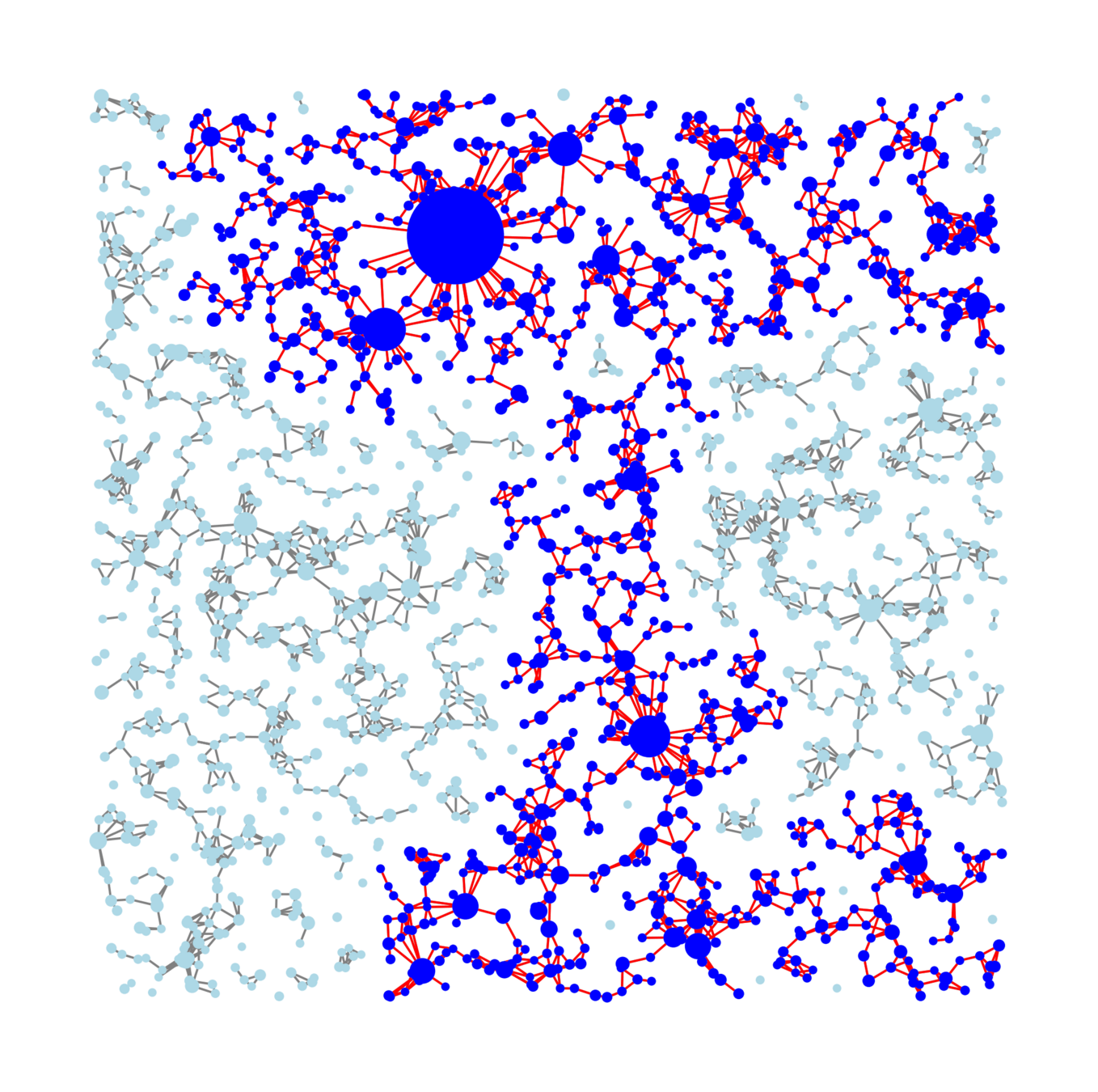
Large deviations (rare events) of cluster sizes

Kernel-based spatial random graphs

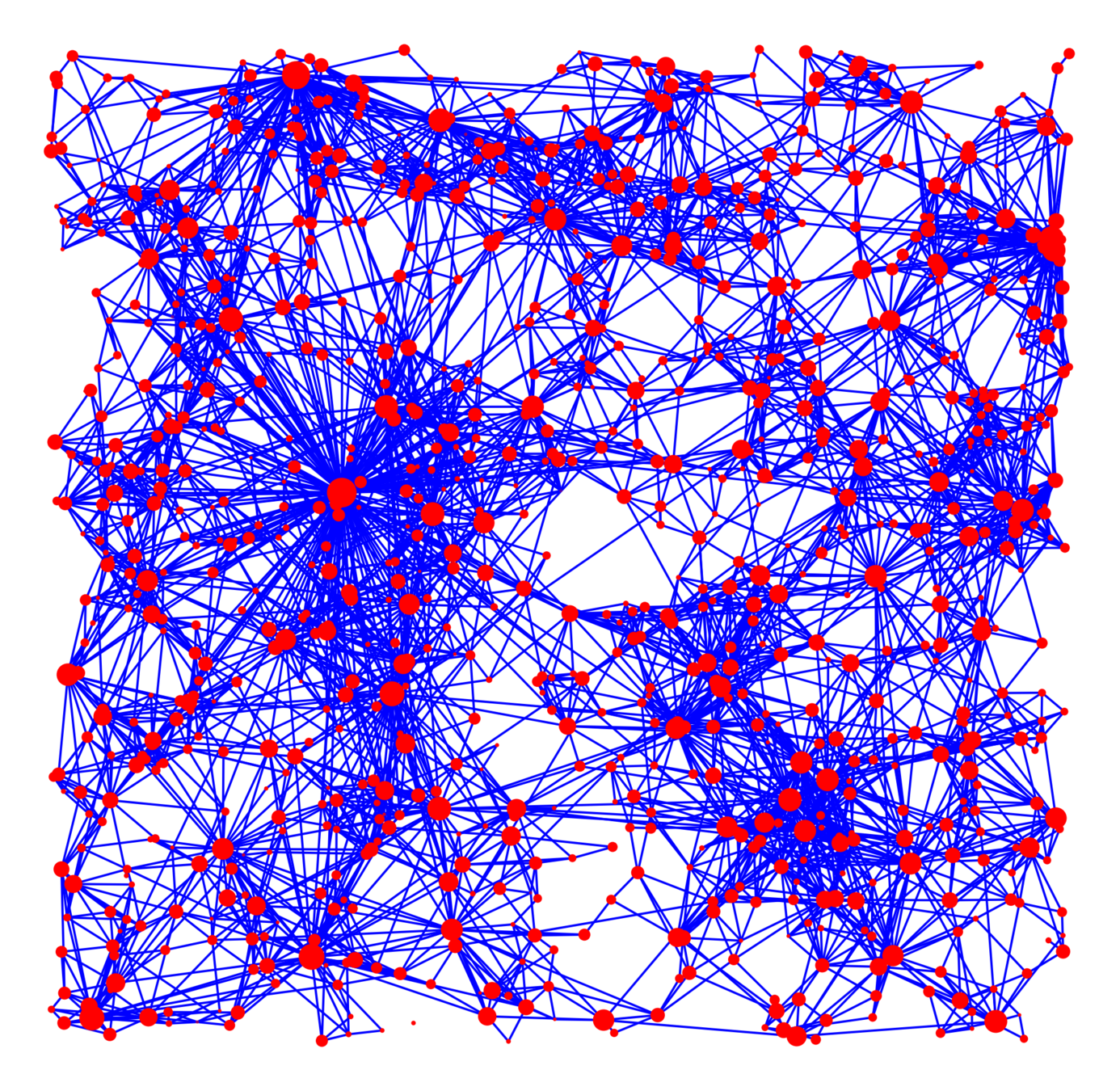
Only four parameters

Vertex set

  • Spatial locations
  • Vertex weights

Edge more likely if

  • Spatially nearby,
  • High weight

Hyperbolic random graph

Scale-free percolation

Long-range percolation

Bond percolation on \(\mathbb{Z}^d\)

\exp\big(-\Theta(\sqrt{n})\big).

Theorem (\(\mathbb{Z}^d\)-like graphs)

[Lebowitz & Schonmann '88; Gandolfi '89; Grimmett, Marstrand '90;

Kesten, Zhang '90; Alexander, Chayes, Chayes, Newman '90; Pisztora '96;
Cerf '97; Contreras, Martineau, Tassion '2024; ...] 
 

Lower tail:
Surface tension drives too small cluster

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \theta-\varepsilon\big)=
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta +\varepsilon\big)= \phantom{\Theta\big(n^{-I(\varepsilon)}\big)}

Upper tail:
Large clusters are very unlikely

\exp(-\Theta(n)\big).

Figure by Tobias Muller

Hyperbolic random graph

Scale-free percolation

Long-range percolation

Bond percolation on \(\mathbb{Z}^d\)

\exp\big(-\Theta(\sqrt{n})\big).

Theorem (\(\mathbb{Z}^d\)-like graphs)

[Lebowitz & Schonmann '88; Gandolfi '89; Grimmett, Marstrand '90;

Kesten, Zhang '90; Alexander, Chayes, Chayes, Newman '90; Pisztora '96;
Cerf '97; Contreras, Martineau, Tassion '2024; ...] 
 

Lower tail:
Surface tension drives too small cluster

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \theta-\varepsilon\big)=
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta +\varepsilon\big)= \phantom{\Theta\big(n^{-I(\varepsilon)}\big)}

Upper tail:
Large clusters are very unlikely

\exp(-\Theta(n)\big).

Question:

Long edges and high-degree vertices,

do they matter?

\exp\big(-\Theta(n^\zeta)\big).

Theorem [J., Komjáthy, Mitsche, '24+] 
We find explicit \(\zeta\in[1/2,1)\), \(\theta\in(0,1)\) s.t.

  • Lower tail: small final size
    If enough long edges or no hubs
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \theta-\varepsilon\big)=
Novelties

  • Reversed discrepancy: large outbreak likelier than small.
  • Long edges can beat surface tension: any         ;
\zeta\!\in\![1/2, 1)
  •   governs second-largest cluster, and cluster of 0
\zeta
  • Techniques: probability, combinatorics, optimization.

What is the influence of long edges and high-degree vertices?

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta +\varepsilon\big)= \phantom{\Theta\big(n^{-I(\varepsilon)}\big)}
  • Upper tail: large final size
    If hubs are present, we find rate funtion \(I(\varepsilon)\): 

What is the influence of long edges and high-degree vertices?

\Theta\big(n^{-I(\varepsilon)}\big).

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

FINAL SIZE

Research plan: Large deviations in percolation and random graphs

Ongoing

Near future

Opportunities Leiden

  • Large deviations  of the giant in inhomogeneous random graphs
    Bert Zwart (CWI)
  • Tall or small trees
    Serte Donderwinkel (Groningen)
  • Applying for CIRM Fellowship
    Luisa Andreis (Milan), 
  • MSc Students (Oxford)
  • Dalia Terhesu

Research plan: Random walks on random graphs

Ongoing

Opportunities Leiden

  • Random friend of a friend tree
    Sofiya Burova (PhD student Barcelona),
    Dieter Mitsche (Santiago de Chile)
  • Cover time of long-range percolation Carlos (MSc student Lima), D. Mitsche
  • (Evolution of) the mixing time of preferential attachment models (PAM)
  • Generating PAMs via random walks
    Rajat Hazra & PhD student

Building a network: Attend and organize workshops, seminars

Near future (invitations)

  • One-world probability seminar
  • Probability meets Combinatorics (IST, Vienna)
  • Long-range phenomena in Percolation (Köln)
  • Mathematical Foundations of Network Models and their Applications (Chennai)

Opportunities Leiden: Lorentz Center

Organisational experience:
RandNET Workshop (with Serte Donderwinkel)

  • 10 days, 80 participants
  • Mini-courses, Open problem sessions (4+ papers)
  • Budget: €55k
  • Attending prof:
    "You set the gold standard for running such an event"

Introduction

By joostjor

Made with Slides.com

Introduction

  • 43

More from joostjor

  • Copy of Largest component in spatial random graphs
    joostjor
    12
  • Largest component in spatial random graphs
    joostjor
    78
  • Largest component in spatial random graphs
    joostjor
    85