Large deviations of the giant in spatial random graphs

 Joost Jorritsma

joint with Júlia Komjáthy, Dieter Mitsche

Probability Seminar University of Oxford, November '24

Supercritical Erdős–Rényi random graph \(G(n, \lambda/n)\)

\mathbb{P}\big(|{\color{green}\mathcal{C}(0)}|>k, {\color{green}\mathcal{C}(0)}\neq {\color{blue}\mathcal{C}_n^{(1)}}\big)\sim
\exp\big(-\Theta(k^{\mathbf{\zeta}})\big)

[Erdős, Rényi '59; O'Connell '98; Andreis, König, Langhammer, Patterson'23]

|{\color{red}\mathcal{C}_n^{(2)}}|\sim_\mathbb{P}(\log n)^{1/\zeta}

Exponential growth of neighbourhood

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)\sim
\exp\big(-\Theta(n^{\mathbf{\zeta}})\big)
\theta(\lambda):=\mathbb{P}(\text{Bienaymé(Poi}_\lambda)\text{ survives})>0
\zeta=1

The largest component

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)\sim
\exp\big(-\Theta(n)\big)

Supercritical bond percolation on \(\mathbb{Z}^d\)

\mathbb{P}\big(k< |{\color{green}\mathcal{C}(0)}|<\infty\big)\sim
\exp\big(-\Theta(k^{\mathbf{\zeta}})\big)

[Alexander, Chayes, Chayes '90; Cerf '00; Gandolfi '88; Grimmett & Marstrand '90, Kesten & Zhang '90, Pisztora '96]

|{\color{red}\mathcal{C}_n^{(2)}}|\sim_\mathbb{P}(\log n)^{1/\zeta}

Surface-tension driven behavior

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)\sim
\exp\big(-\Theta(n^{\mathbf{\zeta}})\big)
\theta(p):=\mathbb{P}(0\leftrightarrow \infty)>0
\zeta=\frac{d-1}d

The largest component

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)\sim
\exp\big(-\Theta(n)\big)

Soft Poisson Boolean model

Edge set \(\mathcal{E}_\infty\)

  • \(\{u\leftrightarrow v \}\Longleftrightarrow \{w_u^{1/d}+w_v^{1/d}\ge \|x_u-x_v\|\}\)
  • Long-range parameter \(\alpha>1\),
  • Percolation \(p\in(0,1]\)

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p\bigg(}\frac{ w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\phantom{\bigg)^{\alpha d}}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{ w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

Vertex set \(\mathcal{V}_\infty\)

  • Locations: Poisson point process intensity \(\beta>0\)
  • Power-law i.i.d. weights \(\tau>2\):
    \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),     \(w\ge 1\)

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

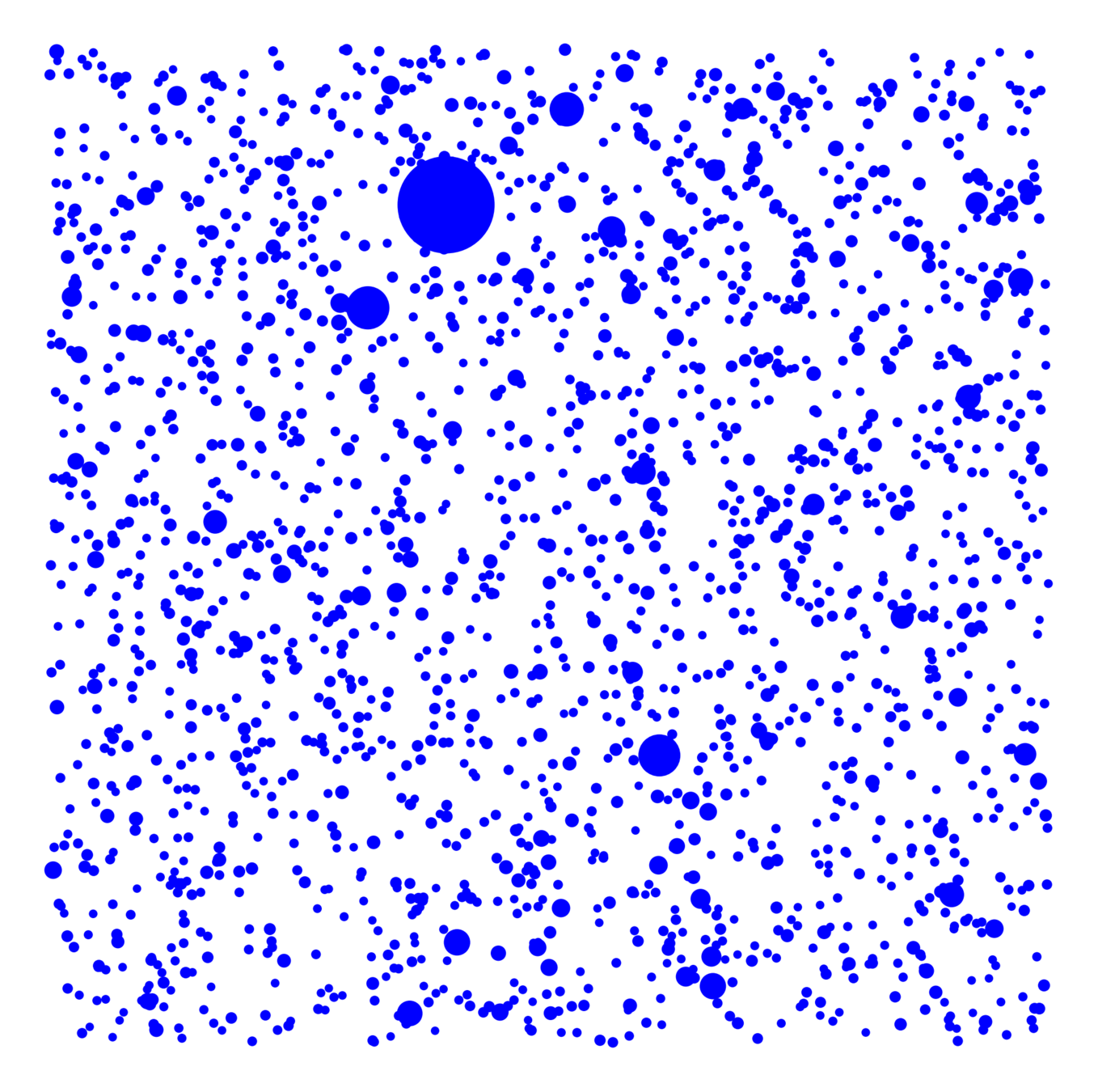
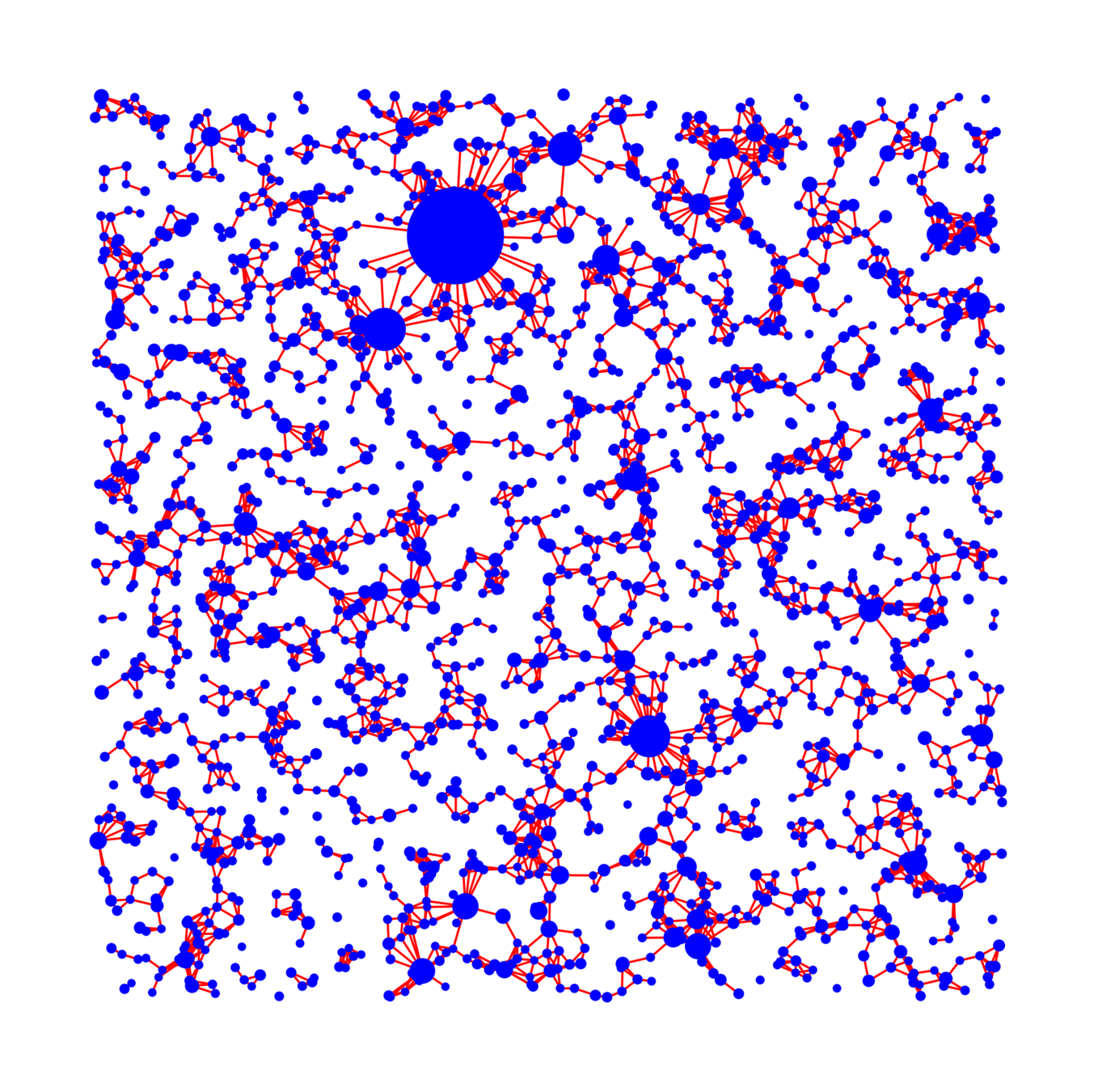
$$(\mathrm{deg}(v) \mid w_v=w) \, = \, \mathrm{Poi}(c_{\alpha, d, \tau}p\beta \cdot w)$$

Soft Poisson Boolean model

Supercriticality assumption 

  • \(\theta=\theta_{d, \tau, \alpha, p}(\beta):=\mathbb{P}_{d, \tau, \alpha, p, \beta}^0(0\leftrightarrow \infty)\)
  • \(\beta>\beta_c(\alpha, \tau, d, p):=\inf\{\beta: \theta(\beta)>0\}\)

Edge set \(\mathcal{E}_\infty\)

  • \(\{u\leftrightarrow v \}\Longleftrightarrow \{w_u^{1/d}+w_v^{1/d}\ge \|x_u-x_v\|\}\)
  • Long-range parameter \(\alpha>1\),
  • Percolation \(p\in(0,1]\)

Vertex set \(\mathcal{V}_\infty\)

  • Locations: Poisson point process intensity \(\beta>0\)
  • Power-law i.i.d. weights \(\tau>2\):
    \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),     \(w\ge 1\)

Soft Poisson Boolean model

Questions:

Fixed parameters: 

  • Point process on \(\mathbb{R}^d\) intensity \(\beta>0\)
  • Power-law exponent \(\tau>2\)
  • Long-range parameter \(\alpha>1\)
  • Percolation \(p\in(0,1]\)

[Gracar, Lüchtrath, Mönch '21]

  • When is \(\beta_c<\infty\)?
    • \(d\ge 2\),
  • Size of the largest connected component \(|\mathcal{C}_n^{(1)}|\)
    • Law of large numbers (\(|\mathcal{C}_n^{(1)}|/n\to \theta\))?
    • surface-tension behav. in \(\mathbb{P}(|\mathcal{C}_n^{(1)}|/n<\theta-\varepsilon)\)?
    • exponential decay of \(\mathbb{P}(|\mathcal{C}_n^{(1)}|/n>\theta+\varepsilon)\)?

or \(d=1\), and \(\alpha\in(1, 2\vee\alpha_\tau)\) 

Power-law weights

Constant weights

Lower tail*:

If \(\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)}\big)
\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee((\tau-1)/\alpha-(\tau-2))}\big)
\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Main result: large deviations for the giant component

*log-corrections at phase transition

Upper tail:

If non-critical

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)
\sim^\ast n^{-I(\theta+\varepsilon)}
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)

*at continuity points of \(I(\theta+\varepsilon)\)

\ggg
\lll
\sim \exp(-n)

Biskup ['04]

\mathbb{P}(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \varepsilon)
\lesssim\exp\big(-n^{2-\alpha-o(1)}\big)

Lower tail: a too small largest component

|{\color{blue}\text{largest}}|/n \overset{\mathbb{P}}\longrightarrow \theta:=\mathbb{P}^0\big(0\leftrightarrow\infty\big)
\mathbb{P}\big(|{\color{blue}\text{largest}}|/n<\vartheta- \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

Goal 1: Law of large numbers

+ local convergence (Giant is almost local)

[vdHofstad, vdHoorn, Maitra '21, vdHofstad '21]

Goal 2: Prove the theorem

\[\lim_{k\to\infty}\lim_{n\to\infty}\mathbb{P}^0(|\mathcal{C}_n(0)|>k, 0\notin\mathcal{C}_n^{(1)}) =0\]

\(|\mathcal{C}_n^{(2)}|=\Theta(\mathrm{polylog}(n))\) 

Edge set \(\mathcal{E}_\infty\)

  • Long-range parameter \(\alpha>1\),
  • Percolation \(p\in(0,1]\)

Connection probability

Vertex set \(\mathcal{V}_\infty\)

  • Locations: Poisson point process intensity \(\beta>0\)
  • Power-law i.i.d. weights \(\tau>2\):
    \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),     \(w\ge 1\)

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n<\vartheta- \varepsilon \big)\lesssim \exp\big(-n^\zeta\big)

Goal 2 Prove

|{\color{blue}\text{largest}}|/n \overset{\mathbb{P}}\longrightarrow \theta
\Longrightarrow

Power-law weights

Constant weights

Lower tail*:

If \(\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\approx\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)}\big)
\approx\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\approx\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee((\tau-1)/\alpha-(\tau-2))}\big)
\approx\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Main result: large deviations for the giant component

*log-corrections at phase transition

Upper tail:

If non-critical

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)
\approx^\ast n^{-I(\theta+\varepsilon)}
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)

*at continuity points of \(I(\theta+\varepsilon)\)

\ggg
\lll
\approx \exp(-n)

Upper tail: polynomial decay when \(\tau<\infty\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)=

Related work:

  • Sum of iid Par(\(\tau)\): principle of single jump.
  • Large deviations # edges \(E_n\) (vdHvdHKMM '24)
    \(\mathbb{P}(E_n>\mathbb{E}[E_n] +n\nu)=^\ast (1+o(1))c_\nu n^{-(\tau-2)\lceil\nu\rceil}\).
  • Inhomogeneous random graphs (J., Zwart '24+)
    \(\mathbb{P}\big(|\mathcal{C}_n^{(1)}|/n>\rho\big)=^\ast (1+o(1))C_\rho n^{-(\tau-2)\lceil \widetilde h(\rho)\rceil}.\) 
\Theta(n^{-(\tau-2)\lceil h(\rho)\rceil})

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+w_v^{1/d}}{\|x_u-x_v\|^d}\wedge 1\bigg)^{d\alpha}$$

Challenge:  Capture dependency on percolation \(p\) 

Power-law weights

Long-range percolation

Lower tail*:

If \(\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)}\big)
\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee( (\tau-1)/\alpha-(\tau-2)}\big)
\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Main result: large deviations for the giant component

*log-corrections at phase transition

Upper tail:

If non-critical, \(\rho\in(\theta, 1)\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)
\sim^\ast n^{-I(\rho)}
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)

*at continuity points of \(I(\rho)\)

\ggg
\lll
\sim \exp(-n)

Supercritical bond percolation on \(\mathbb{Z}^d\)

\mathbb{P}\big(k< |{\color{green}\mathcal{C}(0)}|<\infty\big)\sim
\exp\big(-\Theta(k^{\mathbf{\zeta}})\big)

[Alexander, Chayes, Chayes '90; Cerf '00; Gandolfi '88; Grimmett & Marstrand '90, Kesten & Zhang '90, Pisztora '96]

|{\color{red}\mathcal{C}_n^{(2)}}|\sim_\mathbb{P}(\log n)^{1/\zeta}

Surface-tension driven behavior

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)\sim
\exp\big(-\Theta(n^{\mathbf{\zeta}})\big)
\theta(p):=\mathbb{P}(0\leftrightarrow \infty)>0
\zeta=\frac{d-1}d

The largest component

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)\sim
\exp\big(-\Theta(n)\big)

Lower tail large deviations of the giant*:

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\sim\exp\big(-n^{\zeta}\big)

One decay exponent governing cluster sizes

*log(log)-corrections at phase transition

|{\color{red}\mathcal{C}_n^{(2)}}|
\sim (\log n)^{1/\zeta}

Small components*:

\mathbb{P}\big(k<|{\color{green}\mathcal{C}(0)}|<\infty\big)
\sim \exp\big(-n^{\zeta}\big)
\zeta:=\lim_{n\to\infty}\frac{\log\mathbb{E}[|\text{``downward''-vertex-boundary}(n)|]}{\log n}

If \(\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty\)

If \(\zeta>(d-1)/d\)

Thank you!

  1. Cluster-size decay in supercritical long-range percolation;
    With Júlia Komjáthy, Dieter Mitsche;
    Electronic Journal of Probability (2024).     
  2. Cluster-size decay in supercritical KSRGs;
    With Júlia Komjáthy, Dieter Mitsche; 
    arXiv: 2303.00712, Annals of Probability (to appear).
  3. Large deviations of the giant in supercritical KSRGs;
    With Júlia Komjáthy, Dieter Mitsche;
    Preprint arXiv: 2404.02984.

Kernel-based spatial random graphs

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations \(x_v\in\mathbb{R}^d\): PPP(1),
  • i.i.d. weights \(w_v\ge 1\): Pareto(\(\tau\)),

Edge set \(\mathcal{E}_\infty\)

  • Symmetric kernel \(\kappa(w_1, w_2)\),
  • Edge-density \(\beta>0\),
  • Long-range parameter \(\alpha>1\),

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations \(x_v\in\mathbb{R}^d\): PPP(1), or \(\mathbb{Z}^d\),
  • i.i.d. weights \(w_v\ge 1\): \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),

Edge set \(\mathcal{E}_\infty\)

  • Symmetric kernel \(\kappa(w_1, w_2)\),
  • Edge-density \(\beta>0\),
  • Long-range parameter \(\alpha>1\),
\kappa_\mathrm{prod}=w_uw_v
\alpha\in(1,\infty], d\ge 1

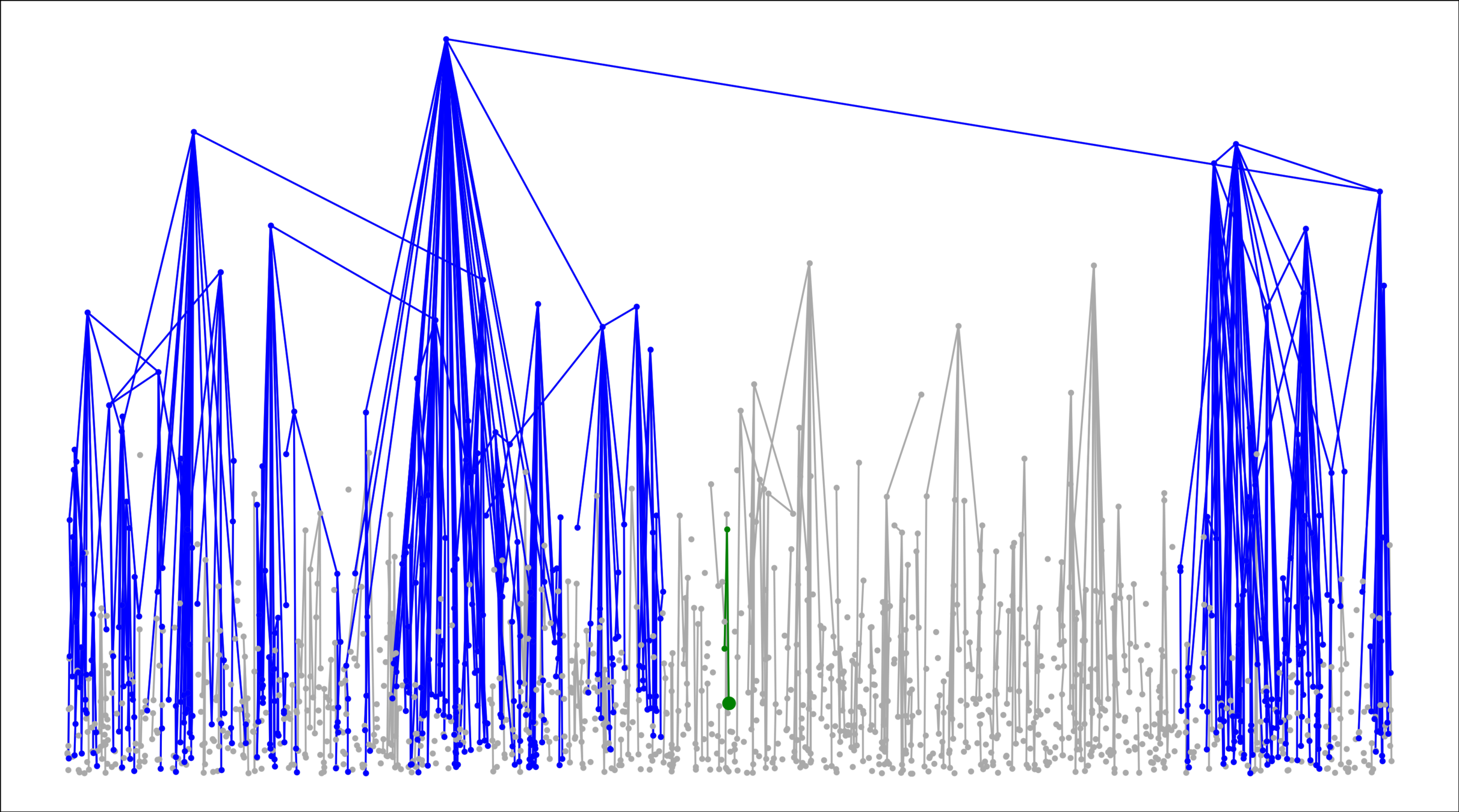
Geom. Inhom. RG

\kappa_\mathrm{prod}=w_uw_v
\alpha=\infty, d= 1

Hyperbolic RG

Geom. RG

\kappa_\mathrm{triv}\equiv 1
\alpha=\infty, d \ge 2

Long-range perc.

\kappa_\mathrm{triv}\equiv 1
\alpha\in(1,\infty), d\ge 1
\kappa_{\max}=w_u\vee w_v

Scale-free Gilbert RG

\kappa_{\mathrm{pa}}=(w_u\vee w_v)
\cdot(w_u\wedge w_v)^{\tau-2}

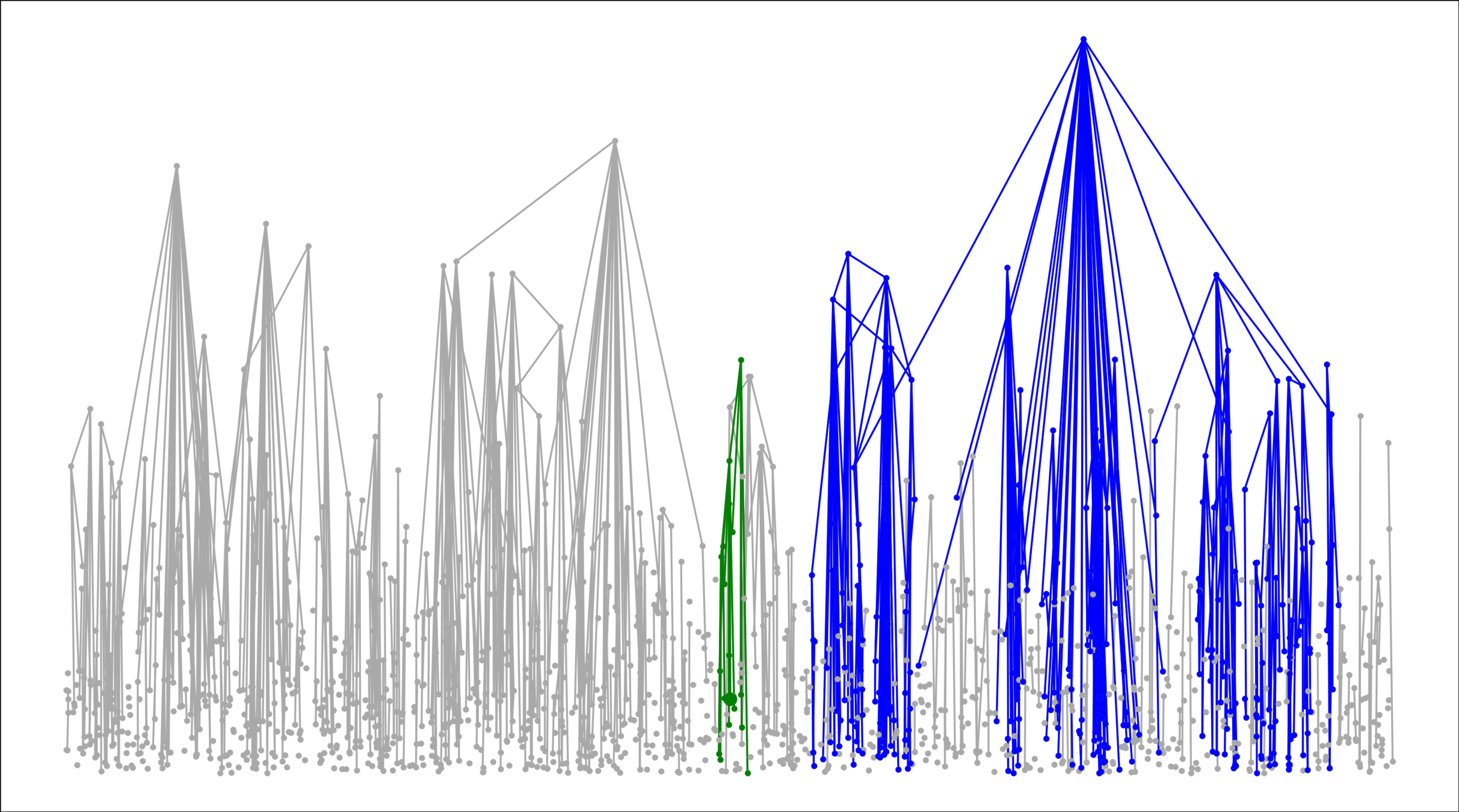
Age-dependent RCM

Theorem. When \(\tau<2\) or \(\alpha<1\):

 

 

  • Infinite degrees
  • Bounded diameter

[Deijfen, v.d. Hofstad, Hooghiemstra '13], [Gracar, Grauer, Lüchtrath, Mörters '18]

[Heydenreich, Hulshof, J. '17], [Hirsch '17], [v.d. Hofstad, v.d. Hoorn, Maitra '22],

[J., Komjáthy, Mitsche, '23], [Lüchtrath '22]

Theorem. When \(\tau>2\) and \(\alpha>1\):  


$$\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau-1)}.$$

\(\tau\) small: many hubs

\(\alpha\) small: many long edges

The interpolating kernel

Connection probability

$${\color{grey}\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta}\frac{\kappa(w_u, w_v)}{\color{grey}\|x_u-x_v\|^d}{\color{grey}\bigg)^\alpha\wedge 1}$$

A parameterized kernel: \(\sigma\ge 0\)

$$\kappa_{\sigma}(w_u, w_v):=\max\{w_u, w_v\}\min\{w_u, w_v\}^\sigma$$

  • \(\tau: \mathbb{P}(w_v\ge w)=w^{-(\tau-1)}.\)
  • \(\sigma\): assortativity
  • \(\sigma\): interpolation
\frac{\sigma}{\tau-1}
\frac1{\tau-1}
1
1
\sigma=\tau-1
\tau=2
\sigma=1
\sigma=1
\sigma=\tau-2
\sigma=\tau-2
\sigma=0
\sigma=0

SFP/GIRG

Hyperbolic RG

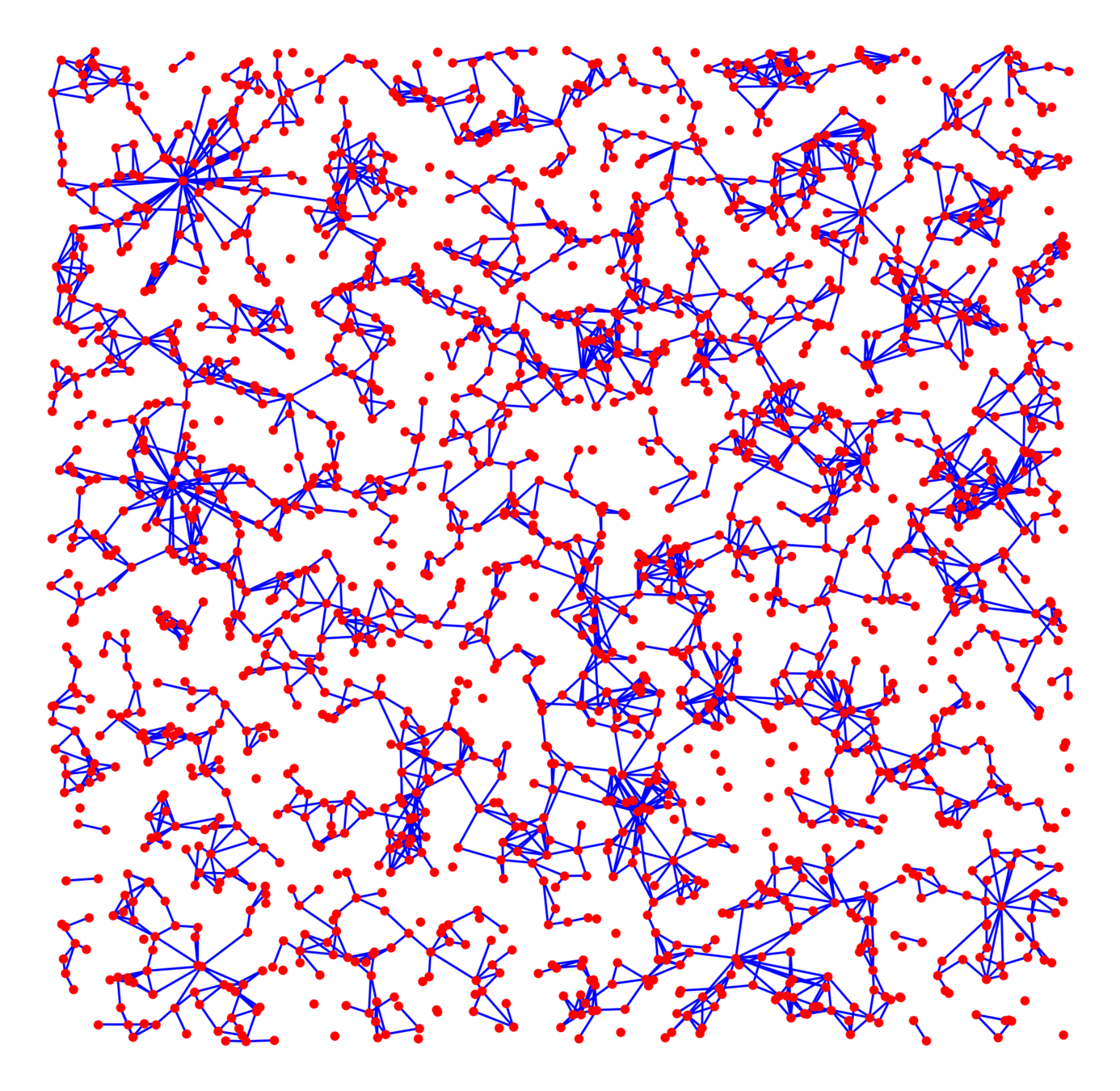
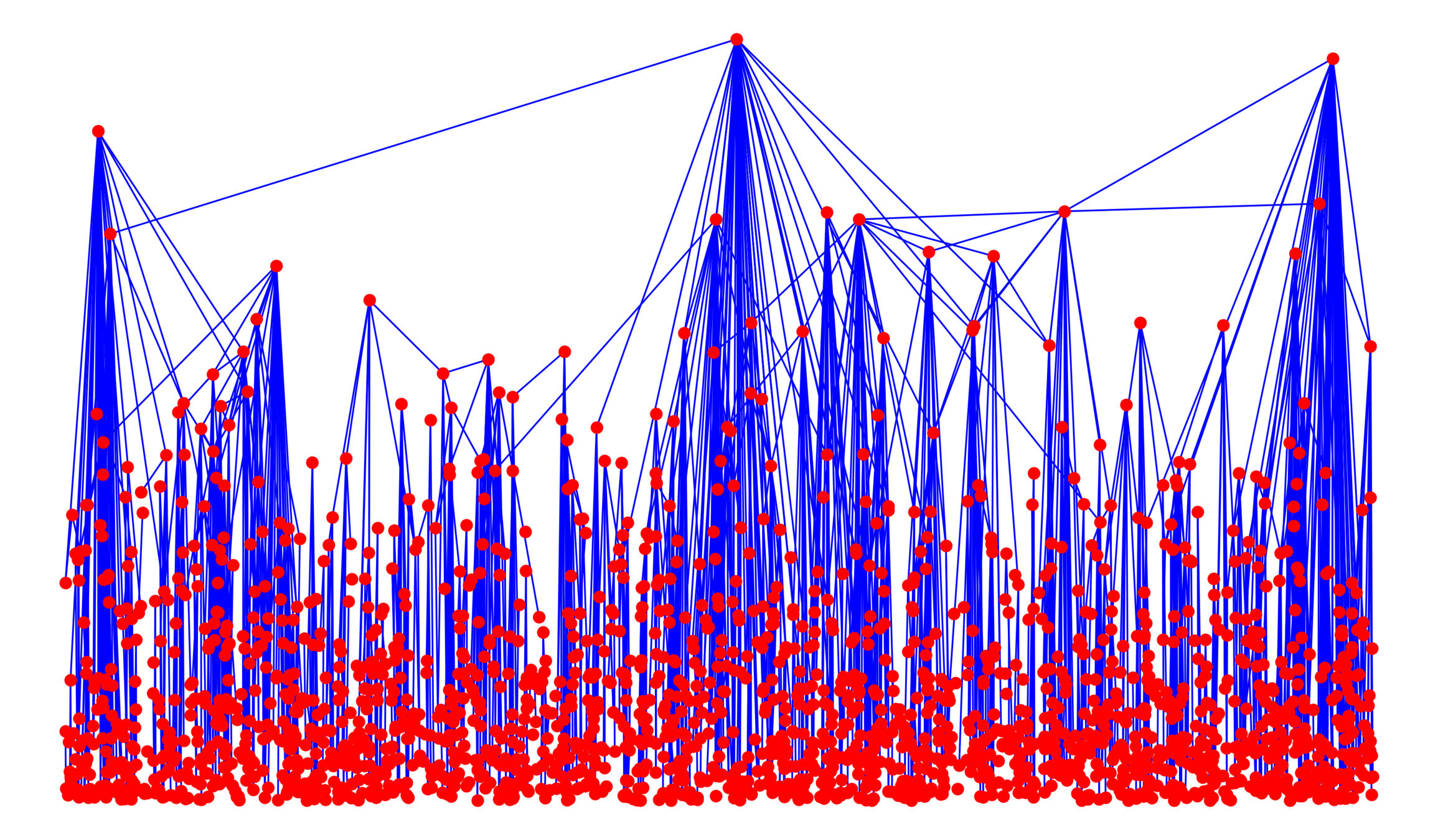
Age-dep. RCM

Scale-free Gilbert

Long-range percolation

Random geom. graph

Nearest-neighbor percolation

Remarks. 

  • \(\zeta_\ast<0\): subcritical*
  • \(d\ge 2\):
    • \((d-1)/d\)
    • partial results: upper bounds
  • Product kernel: 2nd term 

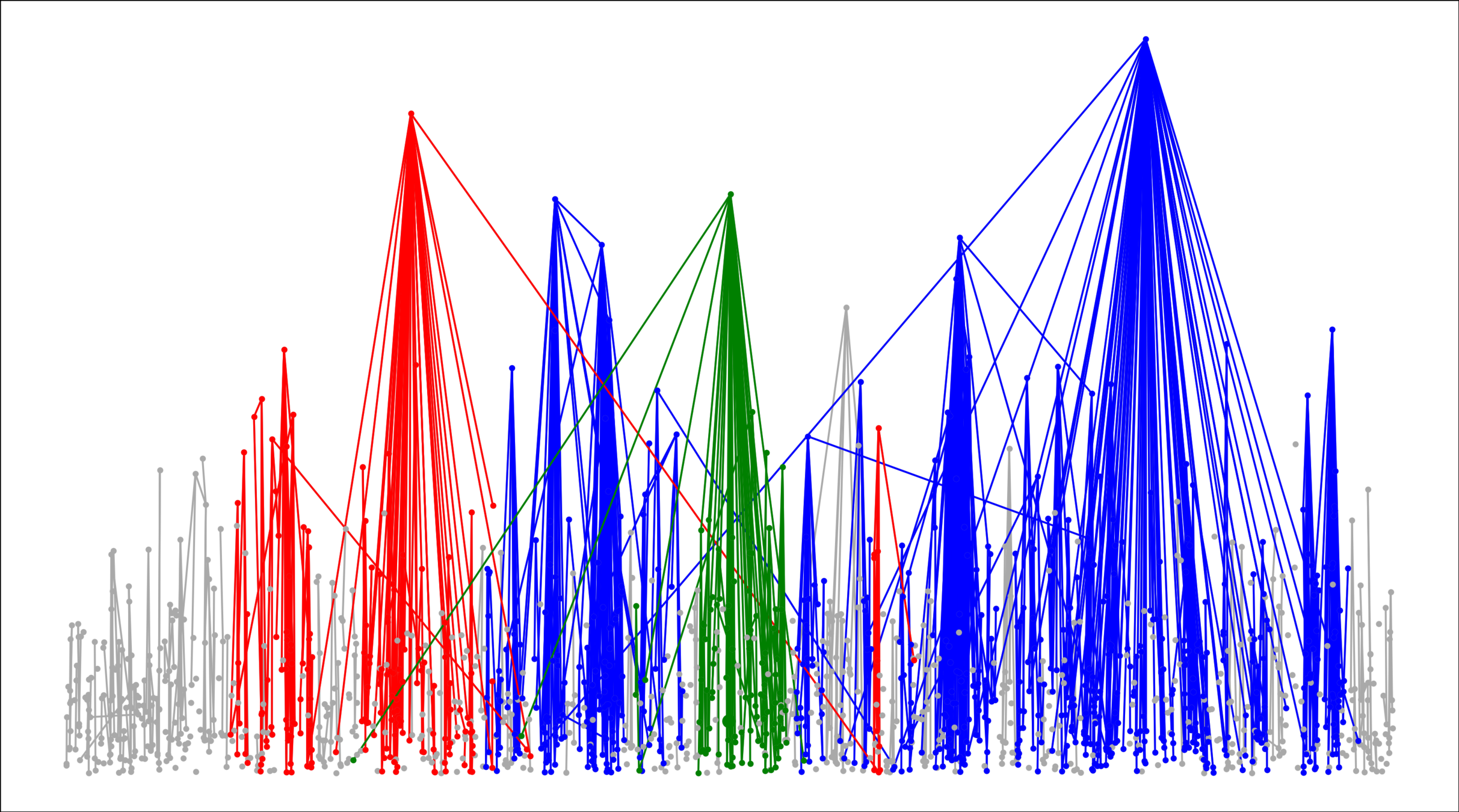
No known results

  • \(|{\color{blue}\text{largest}}|/n\)
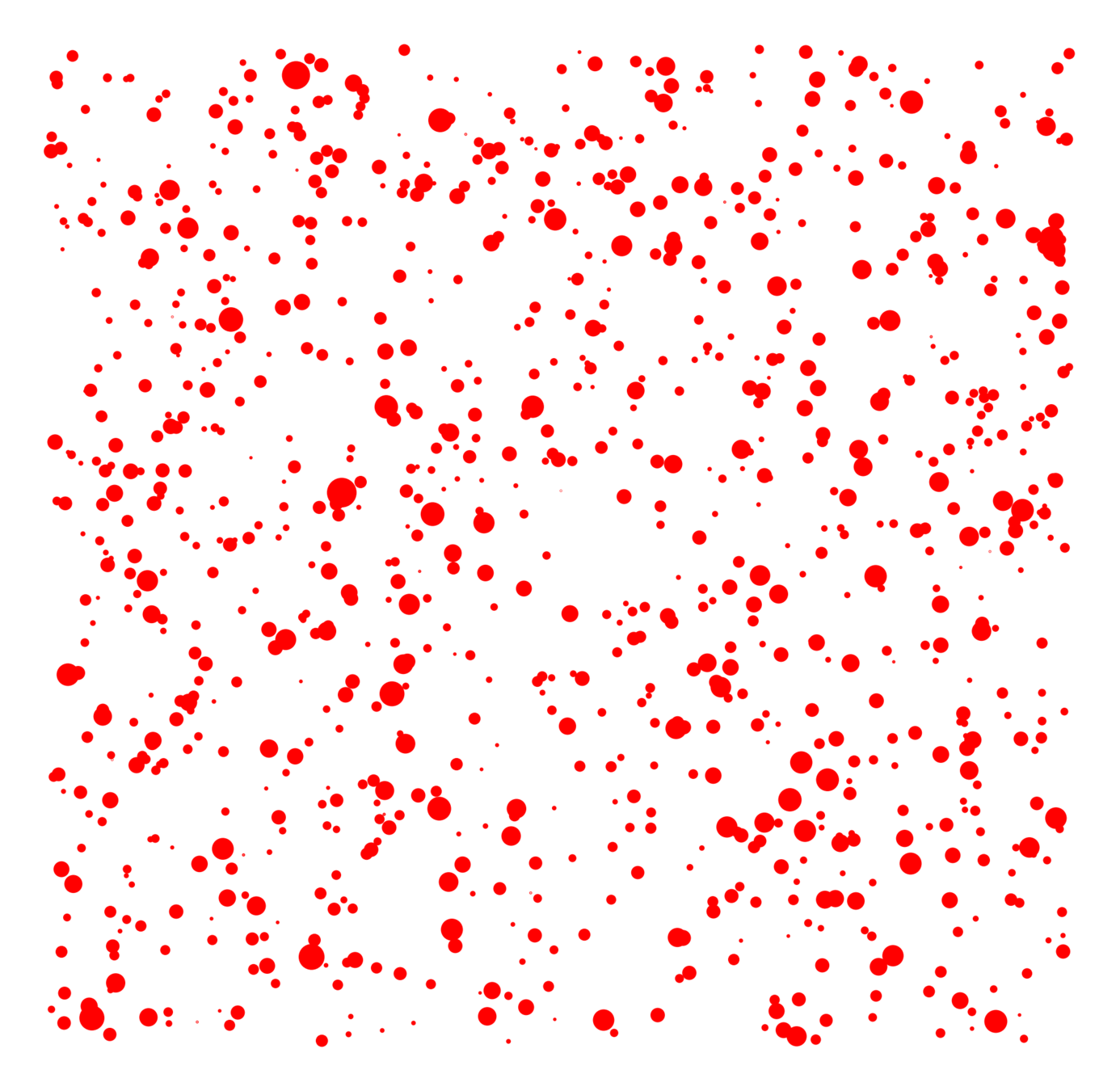
  • \({\color{red}2^{\mathrm{nd}}\text{-largest}}\)

Example 1:

Scale-free Gilbert RG in \(d=1\)

Power-law degrees: \(\tau>2\)

\(d\ge 2\)

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(3\!-\tau)/(2\!-\!(\tau\!-\!1)/\alpha) \}. \end{aligned}

* [Gracar, Lüchtrath, Mönch '22]

 

Theorem. (J., Komjáthy, Mitsche '23+)  

Set

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(\tau\!-\!2)\!-\!(\tau\!-\!1)/\alpha \}. \end{aligned}

If \(\zeta_\ast>0\), then LLN for \(|{\color{blue}\text{largest}}|\), and

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\text{largest}}|\big]}\big)
\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)
\sim \exp\big(\!-\!n^{\color{darkred}\zeta_\ast}\big)
\sim \exp\big(\!-\!n^{\color{darkred}\zeta_\ast}\big)
|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta_\ast}

Long-range parameter: \(\alpha>1\)

\(\kappa_\mathrm{max}=w_u\vee w_v\)

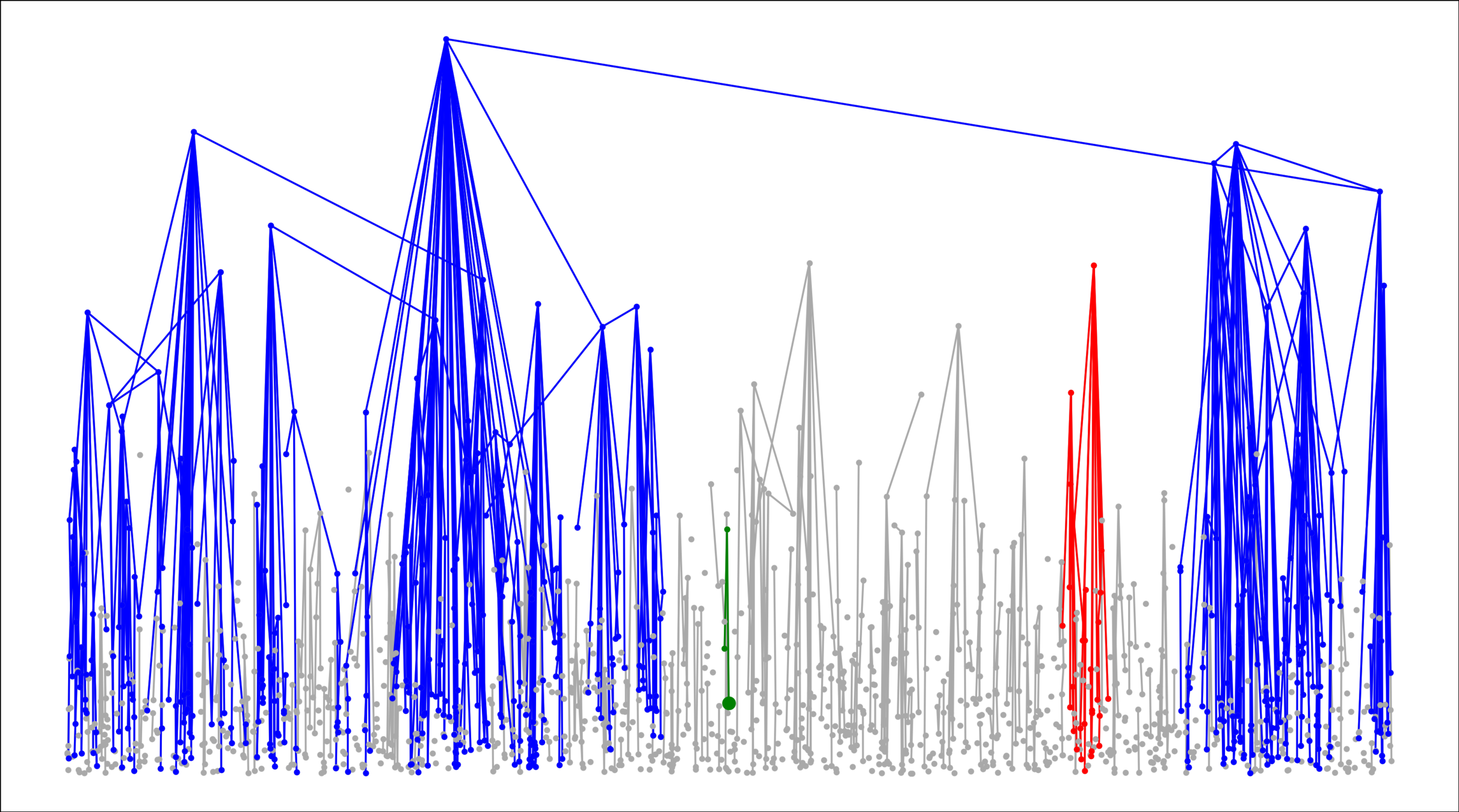
\(\kappa_\mathrm{prod}=w_uw_v\)

Example 2:

Geom. Inhomog. RG  in \(d=1\)

Lower bounds: cluster-size decay

Aim: Find minimal \(\zeta\) s.t.

\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\gtrsim\exp\big(-k^\zeta\big);
\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)
\sim\mathbb{P}\big(\mathcal{Q}_k\text{ isolated}\big)
\sim \exp\big(-k^\zeta\big)
|\mathcal{C}(0)|\ge k
\Bigg\}
\Theta(k)
\mathbb{E}[|\phantom{\square\square}|]\sim\mathbb{E}[|\phantom{\square\square}\leftrightarrow \phantom{\square\square}|]

Aim: Find \(\gamma\) s.t.

\sim k^\zeta

Lower bounds: cluster-size decay

Aim: Find minimal \(\zeta\) s.t.

\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\gtrsim\exp\big(-k^\zeta\big);
|\mathcal{C}(0)|\ge k
\Bigg\}
\Theta(k)
k^\zeta\sim\mathbb{E}\big[|\{v\in\Lambda_k: v\searrow \Lambda_k^c\}|\big]
\mathbb{E}[|\phantom{\square\square}|]\sim\mathbb{E}[|\phantom{\square\square}\leftrightarrow \phantom{\square\square}|]

Aim: Find \(\gamma\) s.t.

\sim k^\zeta

Lower bounds: large deviations

0
n
\Bigg\}
\rho n/2
\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le \rho n\big)
\ge\,\mathbb{P}\big(\text{all }\frac{2}{\rho}\mathcal{Q}_{\tfrac{\rho n}2}\text{-boxes isolated, $\le\!\rho n$ vertices}\big)
\ge\,\Big(\mathbb{P}\big(\mathcal{Q}_{\tfrac{\rho n}2}\text{-box isolated, $\le\!\rho n$ vertices}\big)\Big)^{2/\rho}
\gtrsim\,\exp\big(-\tfrac{2}\rho(\tfrac{\rho n}2)^\zeta\big)

(FKG)

\Bigg\}
n^{1-\varepsilon}
\Bigg\}
(\delta' \log n)^{1/\zeta}
0
n
\mathbb{E}\big[\# \text{small isolated boxes}\big]
\gtrsim\, n^\varepsilon \exp\Big(-\big(\delta \log n)^{1/\zeta}\big)^\zeta\Big)
=\, n^{\varepsilon-\delta}

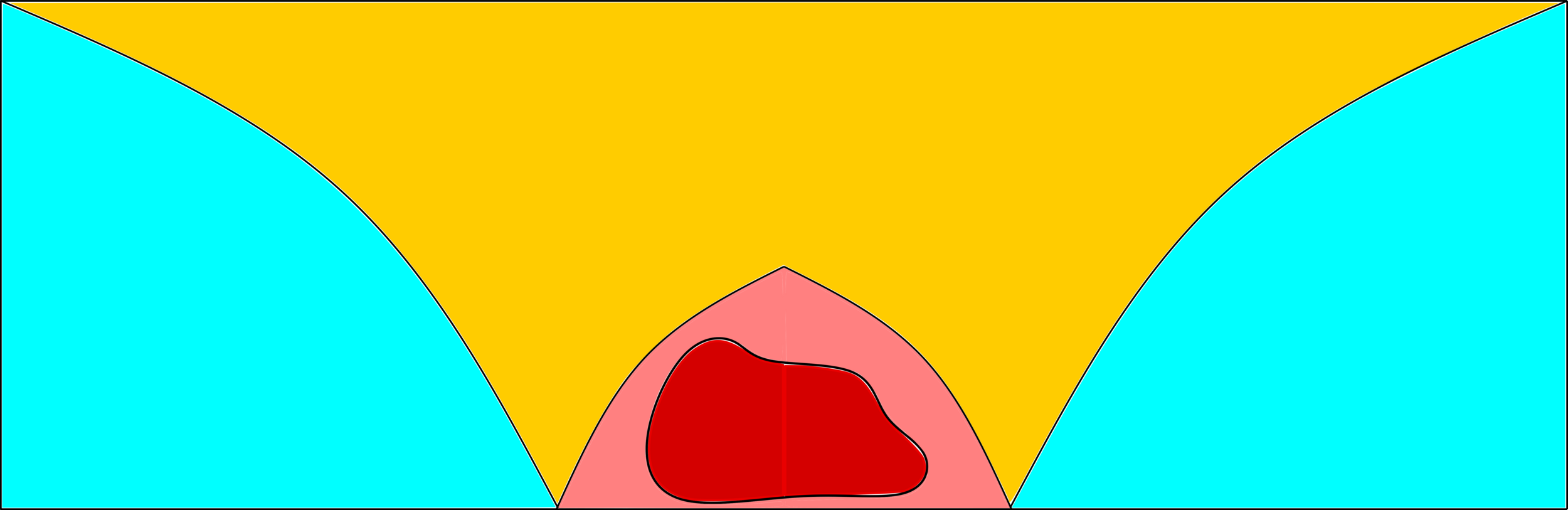
Lower bounds: \(|\mathcal{C}_n^{(2)}|\)

\mathbb{P}\big(|\mathcal{C}_n^{(2)}|\ge (\delta \log n)^{1/\zeta}\big)
\ge \, \mathbb{P}\big(\exists \text{isolated small box, no long edges}\big)
\longrightarrow\,\,\,\, \infty

\(\delta\) small

Kernel-based spatial random graphs

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations, either
    • Lattice \(\mathbb{Z}^d\)
    • Poisson point process (unit intensity)
  • Power-law i.i.d. weights \(w_v\ge 1\):
    \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),

Upper bound: \(|\mathcal{C}_n^{(2)}|\)

\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^{2-\alpha}\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \exp\big(-n^{2-\alpha}\big)
\mathbb{P}\big(\exists\text{ box without giant}\big)
\mathbb{P}\big(\exists\text{ neighboring giants not conn.}\big)
\lesssim (n/k)\exp\big(-k^{2-\alpha}\big)
\lesssim (n/k)\exp\big(-k^{2-\alpha}\big)
\mathbb{P}\big(\nexists\text{ backbone}\big)
\lesssim (n/k)\exp\big(-k^{2-\alpha}\big)
\Bigg\}
k
\lesssim (n/k)(1-(2k)^{-\alpha})^{(\varepsilon k)^2}
\mathbb{P}\big(\text{size-}k\text{ component }\not\leftrightarrow\text{backbone}\big)
\lesssim\phantom{(n/k)}\exp\big(-k^{2-\alpha}\big)
\mathbb{P}\big(\exists \text{size-}k\text{ component }\not\leftrightarrow\text{backbone}\big)
\lesssim(n/k)\exp\big(-k^{2-\alpha}\big)

Soft Poisson Boolean model

Long-range percolation

Bond percolation on \(\mathbb{Z}^d\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta+\varepsilon\big)
\ggg

Lower tail:

- surface tension

- vertex boundary

Long-range percolation

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations, either
    • Lattice \(\mathbb{Z}^d\)
    • Poisson point process (unit intensity)

Edge set \(\mathcal{E}_\infty\)

  • Long-range parameter \(\alpha>1\),
  • Edge-density \(\beta>0\),
  • Percolation \(p\in(0,1]\)

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{\beta}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{\beta}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{\beta}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{\beta}{\|x_u-x_v\|^d}\phantom{\wedge 1}\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p\bigg(}\frac{1}{\|x_u-x_v\|^d}\phantom{\bigg)^\alpha\wedge 1}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p}\bigg(\frac{1}{\|x_u-x_v\|^d}\phantom{\wedge 1}\bigg)^\alpha$$

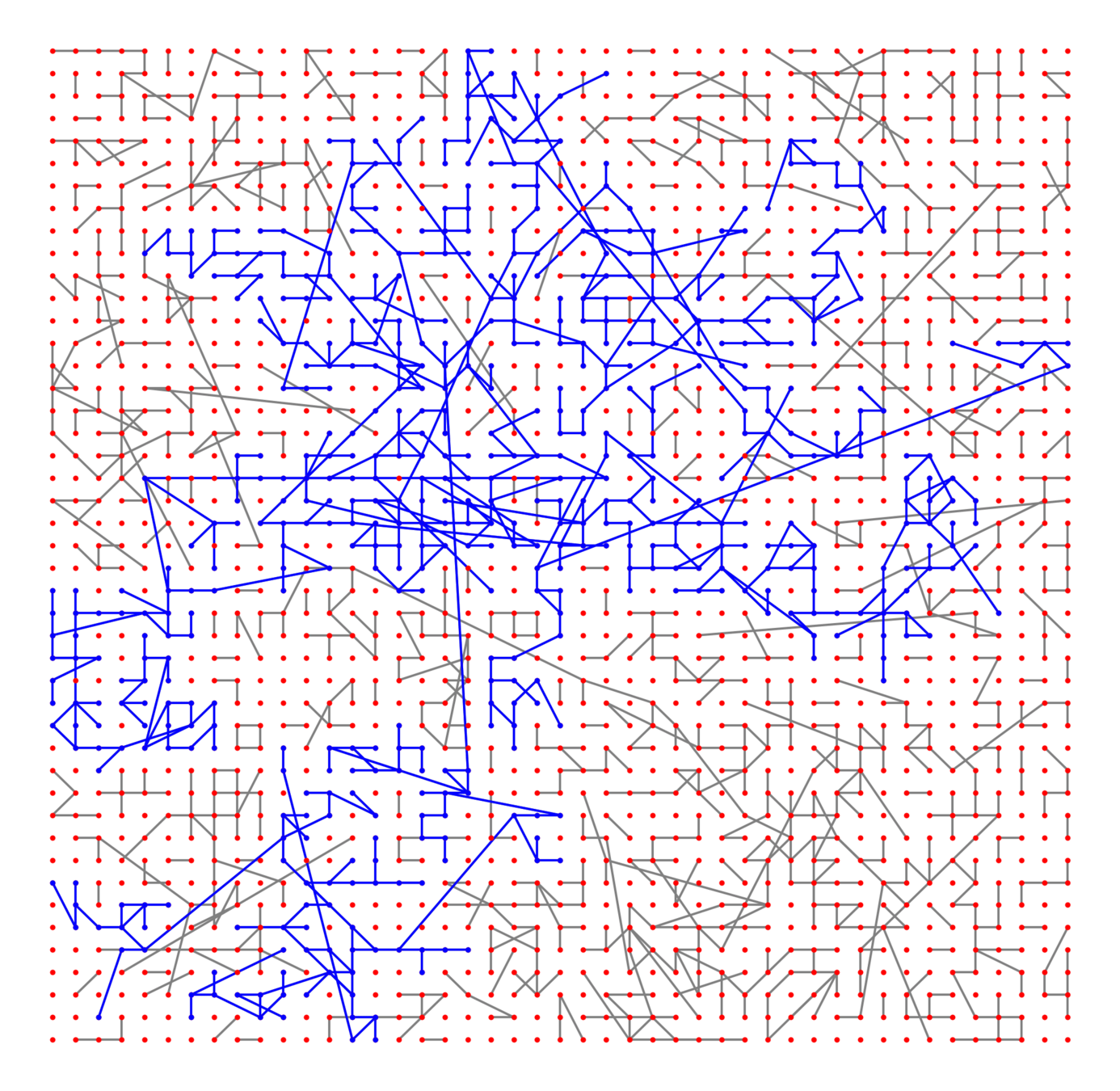
Soft Poisson Boolean model

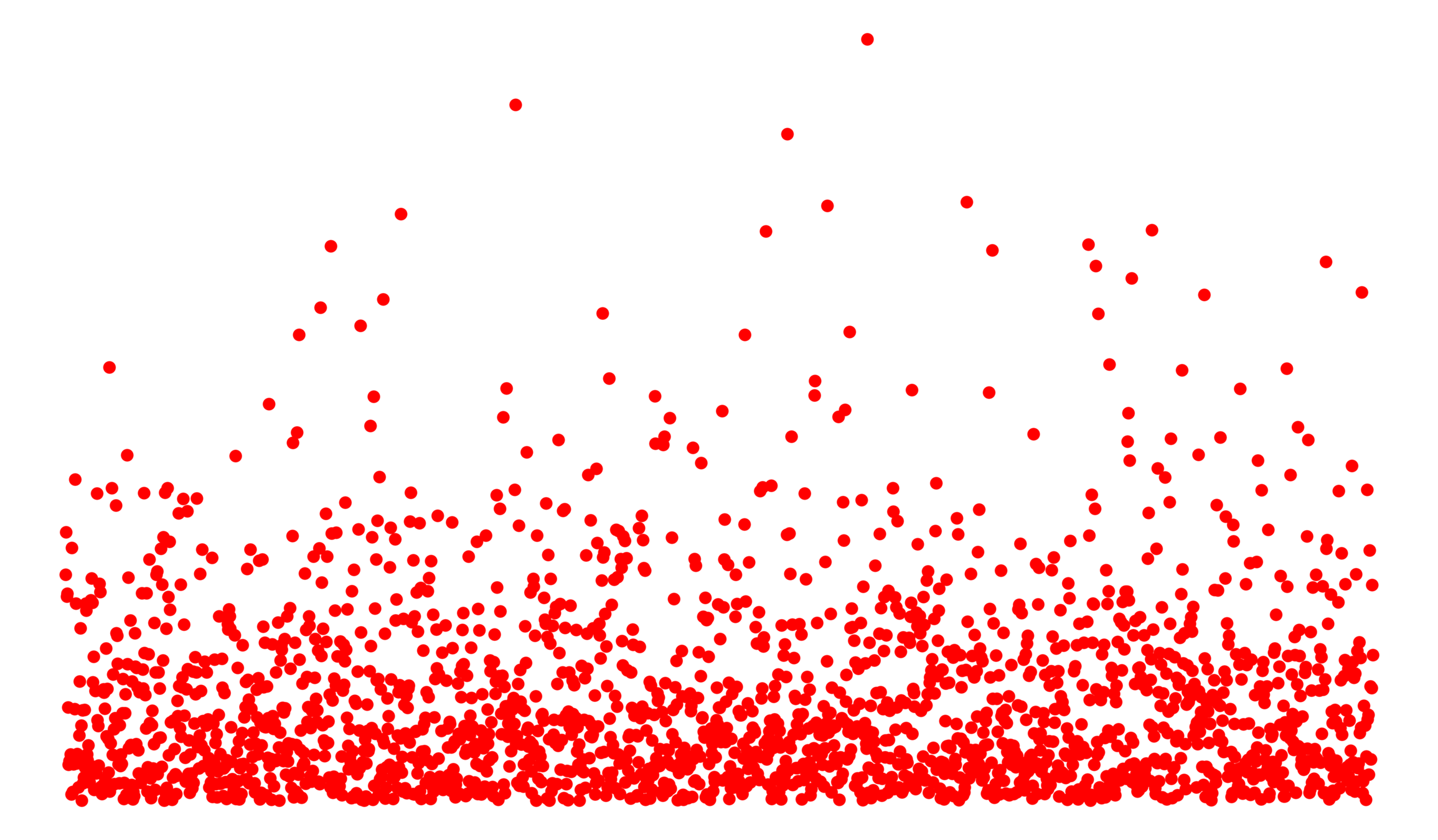
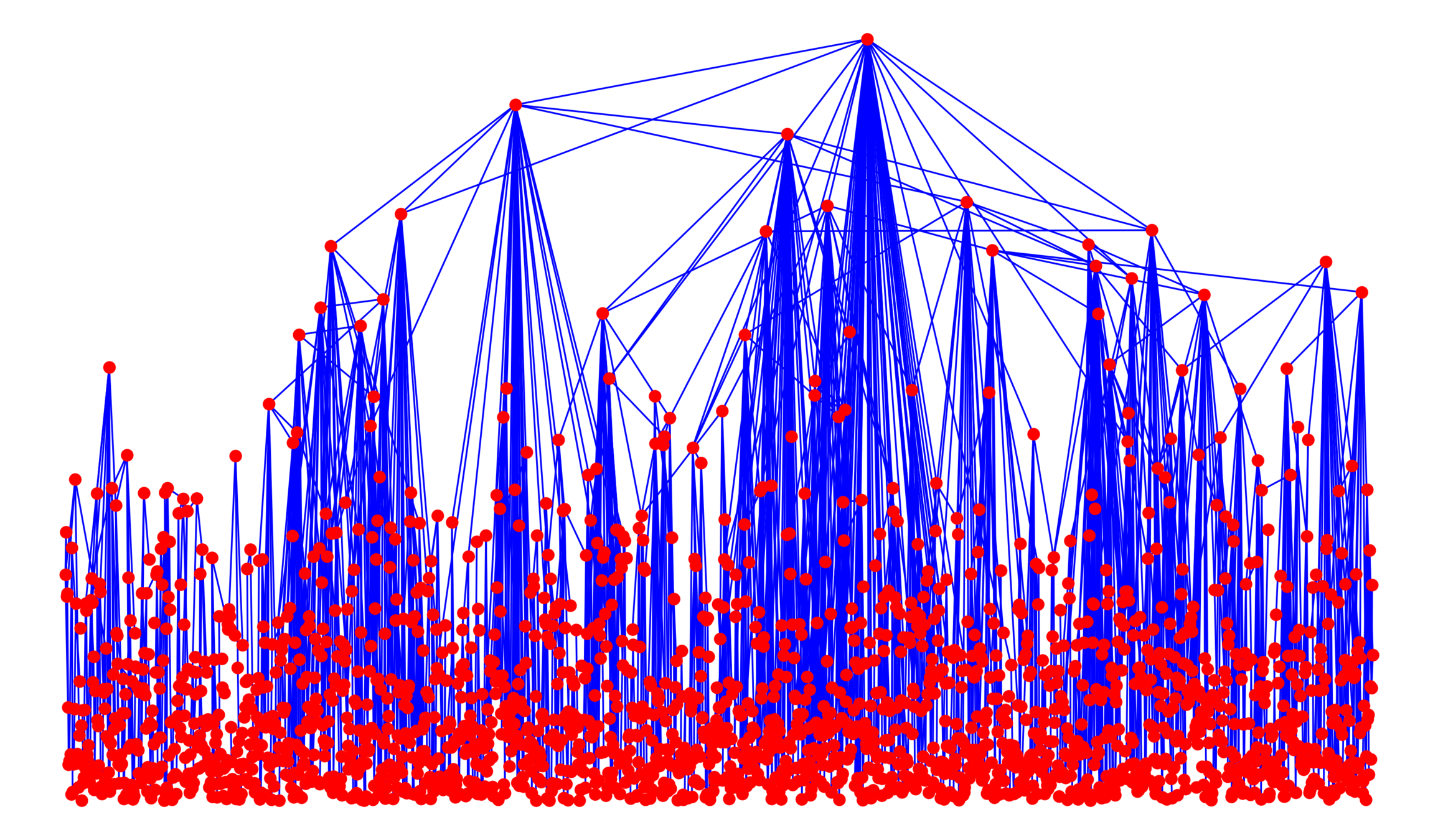
Edge set \(\mathcal{E}_\infty\)

  • Long-range parameter \(\alpha>1\),
  • Percolation \(p\in(0,1]\)

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{ \phantom{w_u^{1/d}+ w_v^{1/d}}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations: Poisson point process intensity \(\beta>0\)
  • Power-law i.i.d. weights \(w_v\ge 1\):
    \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{w_u^{1/d}+ w_v^{1/d}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{ {\color{darkred}w_u^{1/d}+w_v^{1/d}}}{\|x_u-x_v\|}\wedge 1\bigg)^{\alpha d}$$

Kernel-based spatial random graphs

Edge set \(\mathcal{E}_\infty\)

  • Long-range parameter \(\alpha>1\),
  • Edge-density \(\beta>0\),
  • Percolation \(p\in(0,1]\)

Connection probability

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations, either
    • Lattice \(\mathbb{Z}^d\)
    • Poisson point process (unit intensity)
  • Power-law i.i.d. weights \(w_v\ge 1\):
    \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{\beta\cdot (w_u\cdot w_v)}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

Geom. inhom. RG

Long-range percolation

Lower tail*:

If \(\mathbb{E}[\# \text{edges of length } n^{1/d}]\to\infty\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\lesssim\exp\big(-n^{{\color{darkgray}\frac{d-1}d\vee}(2-\alpha)}\big)
\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<\theta-\varepsilon\big)
\sim\exp\big(-n^{\frac{d-1}d\vee(2-\alpha)\vee\frac{3-\tau}{2-(\tau-1)/\alpha}}\big)
\sim\exp\big(-\mathbb{E}[|\mathrm{VB}(n)|]\big)

Remainder: Lower tail LRP - Upper tail GIRG

*log-corrections at phase transition

Upper tail:

If non-critical, \(\rho\in(\theta, 1)\)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)
\sim^\ast n^{-I(\rho)}
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\rho\big)

*at continuity points of \(I(\rho)\)

\ggg
\lll
\sim \exp(-n)
{\color{green}\text{Cluster-size decay}}

Upper bounds

\mathbb{P}\big(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)
\mathbb{P}\big(|{\color{blue}\text{largest}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)
\text{Law of large numbers}
{\text{\color{blue}Lower tail large deviations}}

Challenge: Delocalized components

\binom{n}k \sim n^k \gg n\exp\big(k^\zeta\big)

# possibilities for \(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\)

Components in supercritical graphs

  • Largest component \({\color{blue}\mathcal{C}_n^{(1)}}\):
    • Linear in box size
    • Law of large numbers
    • Lower tail large deviations
    • Upper tail large deviations

Questions


    Component of the origin \({\color{green}\mathcal{C}(0)}\): $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

    Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

Components in supercritical graphs

  • Largest component \({\color{blue}\mathcal{C}_n^{(1)}}\):
    • Linear in box size
    • Law of large numbers
    • Lower tail large deviations
    • Upper tail large deviations

Questions


    Component of the origin \({\color{green}\mathcal{C}(0)}\): $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

    Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

Previous results

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\lesssim(\log n)^{??}
|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}d/(d-1)}
\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)
\sim \exp\!\big(\!\!-\!k^{\color{darkred}(d-1)/d}\big)
\sim \exp\big(\!-\!n^{\color{darkred} (d-1)/d}\big)
\lesssim \exp\big(\!-\!n^{\max(2-\alpha-o(1), (d-1)/d)}\big)
\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! \varepsilon n\big)
\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon)\mathbb{E}[|{\color{blue}\mathrm{largest}}|]\big)

[Alexander & Chayes & Chayes '90],  [Grimmett & Marstrand, '90], [Kesten & Zhang '90], ..., [Deuschel, Pisztora, '96], [Biskup '04], [Penrose '05], [Sly & Crawford'12], [Kiwi & Mitsche '17], [Lichev, Lodewijks, Mitsche, Schapira '22], [Bläsius, Friedrich, Ruff, Zeiff, '23]

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}2/(3-\tau)}
\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! \varepsilon n\big)
\lesssim \exp\big(\!-\!n^{\color{darkred}(3-\tau)/2}\big)

Conjecture: \(\exists \zeta\in \big[\tfrac{d-1}{d},1\big)\):

\sim \exp\big(\!-\!n^{\color{darkred}\zeta}\big)
\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\mathrm{largest}}|\big]}\big)
\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)
\sim \exp\big(\!-\!n^{\color{darkred}\zeta}\big)
|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta}
{\color{green}\text{Cluster-size decay}}
|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}
|{\color{red}2^{\mathrm{nd}}\text{-largest}}| \lesssim (\log n)^{1/\zeta}
{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}
|{\color{blue}\text{largest}}| \text{ linear}
{\color{blue}\text{Lower tail large deviations}}
{\color{blue}\text{Lower tail of large deviations}}
{\color{green}\text{Cluster-size decay}}

Upper bounds

\mathbb{P}\big(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)
\mathbb{P}\big(|{\color{blue}\text{largest}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)
\text{Law of large numbers}
{\text{\color{blue}Lower tail large deviations}}

What about other value \(\zeta_\ast\)?

\zeta_\ast := \max\{2\!-\!\alpha, (3\!-\!\tau)\big/(2\!-\!(\tau\!-\!1)/\alpha) \}

Description of weight distribution in large components

Prevent "small-to-large" merging 

Components in supercritical graphs

  • Largest component \({\color{blue}\mathcal{C}_n^{(1)}}\):
    • Linear in box size
    • Law of large numbers
    • Lower tail large deviations
    • Upper tail large deviations

Answered questions (\(d=1\))


    Component of the origin \({\color{green}\mathcal{C}(0)}\): $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

    Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

(Second-)largest component in supercritical spatial random graphs

  • Cluster-size decay
  • Second-largest component

Open problems:

  • Largest component:
    • Linear in box size
    • Law of large numbers
    • Large deviations

Answered questions (\(d=1\))

  • Phase transition boundaries.
  • Partial results \(d\ge 2\)
  • Extension from PPP to grid
  • Central limit theorem
  • \(\zeta\in\big[(d-1)/d, 1\big)\)
{\color{green}\text{Cluster-size decay}}
|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}
|{\color{red}\mathcal{C}_n^{(2)}}| \lesssim (\log n)^{1/\zeta}
{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}
|{\color{blue}\mathcal{C}_n^{(1)}}| \text{ linear}
{\color{blue}\text{Lower tail large deviations}}
{\color{blue}\text{Lower tail of large deviations}}
\alpha
\tau

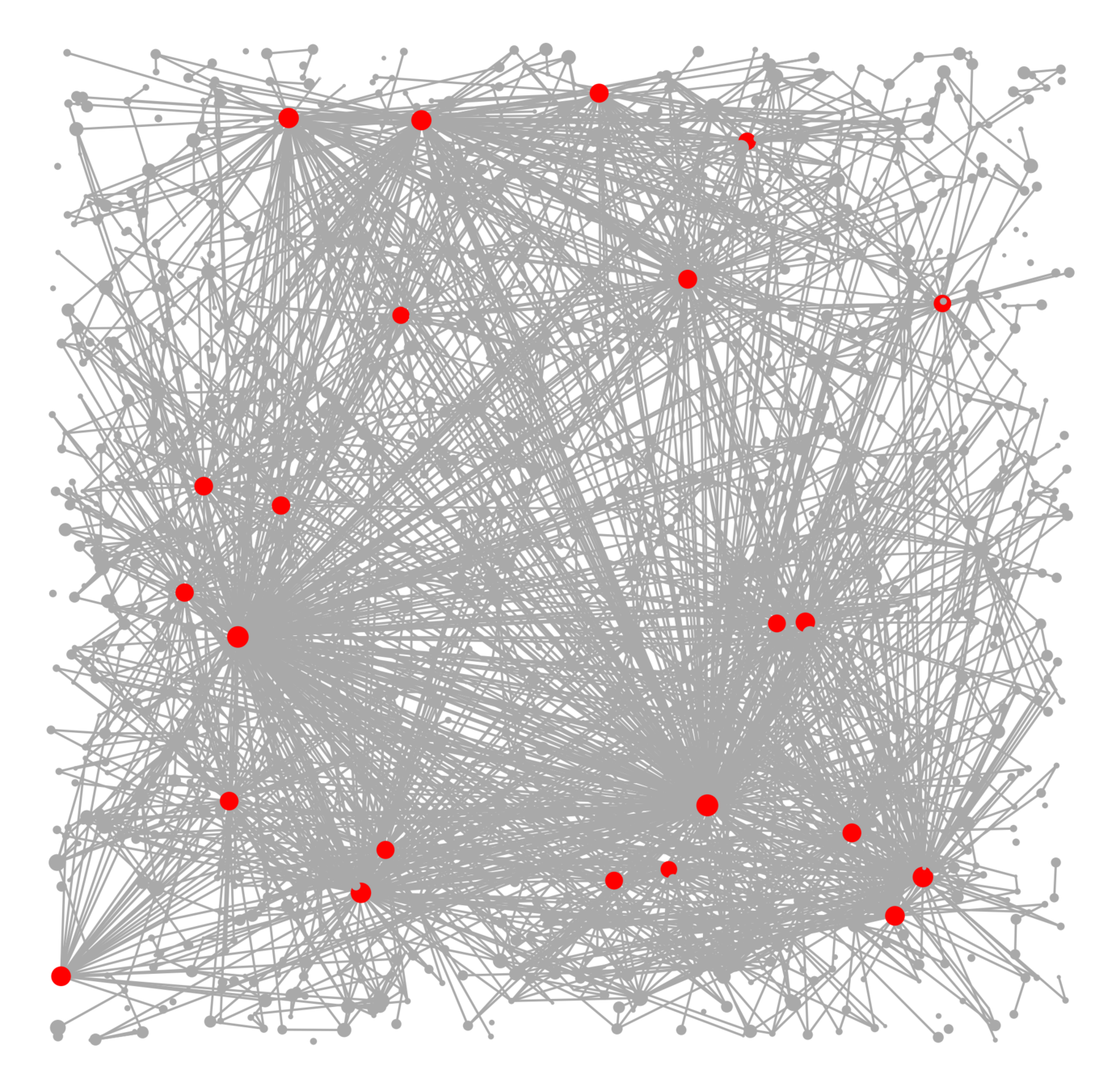
Small

Large

{\color{green}\text{Cluster-size decay}}
|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}
|{\color{red}2^{\mathrm{nd}}\text{-largest}}| \lesssim (\log n)^{1/\zeta}
{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}
|{\color{blue}\text{largest}}| \text{ linear}
{\color{blue}\text{Lower tail large deviations}}
{\color{blue}\text{Lower tail of large deviations}}
\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \lesssim \phantom{n}\exp\big(-k^\zeta\big)
|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \gtrsim \exp\big(-k^\zeta\big)
\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)
|{\color{blue}\mathcal{C}_n^{(1)}}|\! / n \overset{\mathbb{P}, L^1}\longrightarrow \mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta}-\varepsilon\big)\lesssim \exp\big(-n^\zeta\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta} + \varepsilon\big]\big)\gtrsim \exp\big(-n^\zeta\big)
\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \lesssim \phantom{n}\exp\big(-k^\zeta\big)
|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \gtrsim \exp\big(-k^\zeta\big)
\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)
|{\color{blue}\mathcal{C}_n^{(1)}}|\! / n \overset{\mathbb{P}, L^1}\longrightarrow \mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta}-\varepsilon\big)\lesssim \exp\big(-n^\zeta\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta} - \varepsilon\big)\gtrsim \exp\big(-n^\zeta\big)
\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le 2\varepsilon \big)\longrightarrow 0

Remarks. 

  • \(\zeta_\ast<0\): subcritical*
  • \(d\ge 2\):
    • \((d-1)/d\)
    • partial results: upper bounds
  • Product kernel: 2nd term 

Power-law degrees: \(\tau>2\)

\(d\ge 2\)

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(3\!-\tau)/(2\!-\!(\tau\!-\!1)/\alpha) \}. \end{aligned}

* [Gracar, Lüchtrath, Mönch '22]

 

Theorem. (J., Komjáthy, Mitsche '23+)  

Set

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(\tau\!-\!2)\!-\!(\tau\!-\!1)/\alpha \}. \end{aligned}

If \(\zeta_\ast>0\), then LLN for \(|{\color{blue}\text{largest}}|\), and

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\text{largest}}|\big]}\big)
\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)
\sim \exp\big(\!-\!n^{\color{darkred}\zeta_\ast}\big)
\sim \exp\big(\!-\!n^{\color{darkred}\zeta_\ast}\big)
|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta_\ast}

Long-range parameter: \(\alpha>1\)

Example 2:

Geom. Inhomog. RG  in \(d=1\)

Hyperbolic random graph

Scale-free percolation

Long-range percolation

Scale-free Gilbert RG

Random geom. graph

Nearest-neighbor percolation

Largest component in spatial random graphs

By joostjor

Made with Slides.com

Largest component in spatial random graphs

  • 77

More from joostjor