データ同化における推定誤差解析の現状と課題
○竹田 航太 (名古屋大学)
This was supported by RIKEN Junior Research Associate Program and JST SPRING JPMJSP2110.
(T.2025) K. T., Error analysis of the projected PO method with additive inflation for the partially observed Lorenz 96 model, arXiv preprint, https://doi.org/10.48550/arXiv.2507.23199.
限られた情報
「現実」
観測値
y_n = H u_n + \eta_n
(u_n)_n
観測
モデル
カオス
生成
u_n = \Psi(u_{n-1})
推定値
(v_n)_n
データ同化
データ同化とは
→ 本講演は時系列推定に焦点を当てる
離散時間時系列推定
Observing System Simulation Experiment (OSSE)
まず，データ同化の有効性を検証する標準的な枠組み
を紹介．
仮想的な真の状態を作って状態推定精度を評価．
双子実験とも呼ばれる．
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
u_1
u_2
u_3
(1) モデルから真の時系列を 生成
u_n
\mathbb{R}^{N_u}
離散時間時系列推定
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
u_1
u_2
u_3
(2) 観測値 を生成
y_n
y_1
y_2
y_3
\mathbb{R}^{N_u}
離散時間時系列推定
(1) モデルから真の時系列を 生成
u_n
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
v_n
(3) 観測値 を同化し解析値（推定値） を計算
y_n
v_1
v_2
v_3
y_1
y_2
y_3
データ同化アルゴリズム
\mathbb{R}^{N_u}
離散時間時系列推定
(2) 観測値 を生成
y_n
(1) モデルから真の時系列を 生成
u_n
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
\mathbb{R}^{N_u}
v_1
v_2
v_3
(4) 真値 と解析値 の差 を計算
u_n
v_n
e_1
e_2
e_3
u_1
u_2
u_3
v_n
(3) 観測値 を同化し解析値（推定値） を計算
y_n
e_n
離散時間時系列推定
(2) 観測値 を生成
y_n
(1) モデルから真の時系列を 生成
u_n
データ同化と定式化
EnKF
同期
フィルタ
3DVar
連続時間
離散時間
ノイズあり
ノイズなし
時間依存重み
固定重み
重み 1
時系列データ同化 → 時系列観測を予測値に重みつきで混ぜる．
ある観点からは．．．
同期
フィルタ
観測頻度
観測ノイズ
定式化とアルゴリズム
逆問題における正則化パラメータに対応
ノイズ強度に応じて重みを調整
重要
・・・4つをこれから説明
①
②
③
④
基本はこれを
解析したい
「現実」
観測値
y_n = H u_n + \eta_n
(u_n)_n
観測
モデル
カオス
生成
u_n = \Psi(u_{n-1})
EnKFに対し，Filter accuracyを示した．(T.+2024)
\le C \cdot
推定誤差
推定値
(v_n)_n
データ同化
EnKF
Filter accuracy
観測誤差
昨年度のRIMS
離散時間ノイズあり
限られた情報
「現実」
観測値
y_n = H u_n + \eta_n
(u_n)_n
観測
モデル
カオス
生成
u_n = \Psi(u_{n-1})
EnKFに対し，Filter accuracyを示した．(T.+2024)
推定値
(v_n)_n
データ同化
EnKF
Filter accuracy
仮定：離散化誤差なし
定式化やアルゴリズムが様々
この目標で精度が保証されるか？
H=I
仮定：
\le C \cdot
推定誤差
観測誤差
課題は多い
限られた情報
観測値
y_n = H u_n + \eta_n
モデル
u_n = \Psi(u_{n-1})
EnKFに対し，Filter accuracyを示した．(T.+2024)
仮定：離散化誤差なし
H=I
仮定：
Filter accuracy
誤差解析
\le C \cdot
推定誤差
観測誤差
この目標で精度が保証されるか？
→ C < 1を示せるか？位相が改善するか？
データ同化
EnKFアルゴリズム
定式化やアルゴリズムが様々
確率微分方程式，偏微分方程式，離散時間力学系．．．
それぞれで似たアルゴリズムが解析されている
課題は多い
観測値
y_n = H u_n + \eta_n
モデル
u_n = \Psi(u_{n-1})
EnKFに対し，Filter accuracyを示した．(T.+2024)
仮定：離散化誤差なし
H=I
仮定：
Filter accuracy
誤差解析
\le C \cdot
推定誤差
観測誤差
この目標で精度が保証されるか？
→ C < 1を示せるか？位相が改善するか？
データ同化
EnKFアルゴリズム
定式化やアルゴリズムが様々
確率微分方程式，偏微分方程式，離散時間力学系．．．
それぞれで似たアルゴリズムが解析されている
課題は多い
1. 観測条件の緩和
2. アルゴリズム間の関係
3. 離散化誤差の考慮
本講演
1. 観測条件の緩和（部分観測）
1. 「偏微分方程式的」ノイズなし定式化 (Azouani+2014)
2. 2D Navier-Stokes + EnKF (Biswas+2024arXiv)
3. Lorenz 96 + EnKF (T.2025arXiv)
H=I
問い
H=O
追跡可能
追跡不可能
この間は
どうなっているか？
結果 部分観測下での追跡可能性（filter accuracy)
ノイズありかつ複雑なアルゴリズムでも「追跡可能」を証明．
これはどの定式化にも共通する問い
①
④
④'
アルゴリズム①
y_t = H u_t, \quad t > 0
（連続時間）同期フィルタ
P = H^* H, Q = I - P
p_t = y_t, \quad \frac{d q_t}{dt} = Q \mathcal{F(v_t)}
真の時系列
観測
データ同化アルゴリズム
v_t = p_t + q_t \in \operatorname{ran}(P) \oplus \operatorname{ran}(Q).
→ 推定値
射影
\mathcal{Y} \subset \mathcal{X},
観測空間
H \in \mathcal{L}(\mathcal{X}, \mathcal{Y}),
部分等長
\tau > 0
観測間隔
連続時間ノイズなし
\mathcal{X}
Hilbert空間 上の発展方程式
\frac{du_t}{dt}=\mathcal{F}(u_t), \quad t > 0
観測空間で常に同期
u_0 \in \mathcal{X}
(Law+2016)
有界線形
観測空間
\oplus
未観測空間
例：Lorenz 96モデル
\frac{du^i}{dt} = (u^{i+1} - u^{i-2}) u^{i-1} - u^i + F,
Lorenz 96 (L96)
N_u \ge 4, \bm{u} = (u^i)_{i=1}^{N_u} \in \mathbb{R}^{N_u}, F \in \R,
非線形・エネルギー保存
線形・散逸
外力
地球の等緯度常に分布する物理量のカオスな変動を模した現象論的モデル．
(Lorenz1996)(Lorenz+1998)
u
(i = 1, \dots, N_u)
u^{0} = u^{N_u}, u^{-1} = u^{N_u - 1}, u^{N_u+1} = u^1.
- 気象データ同化でよく用いられるトイモデル．
- エネルギー散逸性が重要:
\frac{d}{dt}|u|^2 \le -|u|^2 + 2N_u F^2
※ 実数の絶対値とベクトルのユークリッドノルムの両方に
|\cdot|
を用いる．
例：L96の特別な部分観測
L96モデルに対して，以下の部分観測を考える．
N_u = 3N
(\phi_i)_{i=1}^{N_u} \subset \mathbb{R}^{N_u}
イラスト
○
○
×
○
○
×
○
○
×
○
○
×
○: 観測
×: 観測しない
u^1
u^2
u^3
u \in \mathbb{R}^{3N}
N_u = 3N, N_y = 2N
N \in \mathbb{N}
H = [\phi_1, \phi_2, \phi_4, \phi_5, \phi_7, \dots]^\top \in \mathbb{R}^{N_y \times N_u}.
に対し
とする．
ただし，
は標準基底である．
H = [\phi_1, \phi_2, \phi_4, \phi_5, \phi_7, \dots]^\top
(\spadesuit)
(\mathcal{X} = \mathbb{R}^{N_u})
例：L96モデルと観測
時空間プロット
N_u = 60, F = 8.0, dt = 0.01
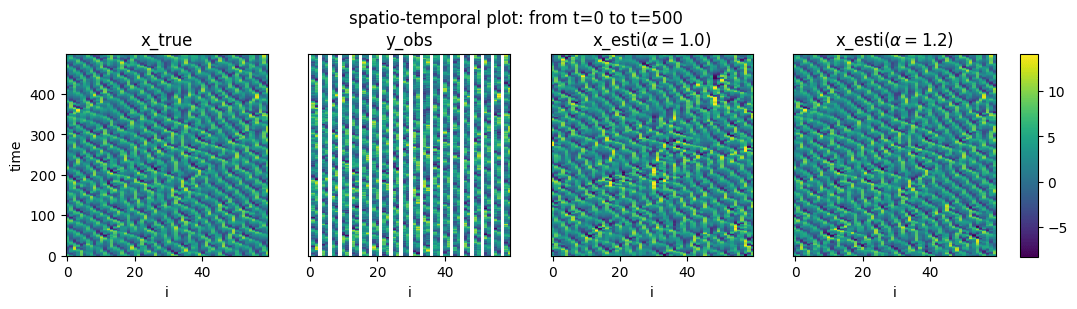
既存結果：連続時間同期フィルタ
定理
(Theorem4.5 in Law+2016の改変)
注意
方程式と観測の組み合わせが重要．
e^{-2t}.
収束レート：
観測行列は外力に依存しない．
\textstyle{\lim_{t \rightarrow \infty}}|v_t - u_t|^2 = 0.
: Lorenz 96モデルの真の軌道
u_t
v_t
: 観測行列 と連続時間同期フィルタによる推定値
このとき，任意の初期推定値 について
v_0
※ 実数の絶対値とベクトルのユークリッドノルムの両方に
|\cdot|
を用いる．
(\spadesuit)
+いくつかの仮定
任意の で2/3観測 で十分．
F
(\spadesuit)
アルゴリズム④
EnKF (Ensemble Kalman filter)
真の時系列
データ同化アルゴリズム
v_n = \overline{v}_n = \textstyle{\frac{1}{m} \sum_{k=1}^m} v_n^{(k)}
→ 推定値
\mathcal{X}
Hilbert空間 上の発展方程式
\frac{du_t}{dt}=\mathcal{F}(u_t), \quad t > 0
u_0 \in \mathcal{X}
y_n = H u_{n\tau} + \xi_n, \quad n \in \mathbb{N}
\mathcal{Y} \subset \mathcal{X},
観測空間
観測
H \in \mathcal{L}(\mathcal{X}, \mathcal{Y}),
部分等長
\tau > 0
観測間隔
離散時間ノイズあり
(Burgers+1998)
\text{更新式}
v_n^{(k)} \ (k=1, \dots, m)
個の推定サンプル
m
①ランダムノイズ
②有界ノイズ
\sim \mathcal{N}(0, r^2 I_{N_y})
|\xi_n| \le \epsilon
アルゴリズム④
EnKF (Ensemble Kalman filter)
データ同化アルゴリズム
v_n = \overline{v}_n = \textstyle{\frac{1}{m} \sum_{k=1}^m} v_n^{(k)}
→ 推定値
y_n
\tau > 0
観測間隔
離散時間ノイズあり
(Burgers+1998)
v_n^{(k)} = \text{重み付き平均}(\Psi_\tau(v^{(k)}_{n-1}), y_n; \widehat{P}_n^{\alpha})
v_n^{(k)} \ (k=1, \dots, m)
個の推定サンプル
m
\widehat{P}_n^{\alpha} = \operatorname{Cov}_m(\{\Psi_\tau(v_{n-1}^{(k)})\}_{k=1}^m) + \alpha^2 I
重みは共分散 に依存．
チューニングパラメータ
\alpha
で正則化
= \text{重み付き平均}(\text{予測}, \text{観測}; \text{予測のばらつき})
時間依存する重み．サンプル共分散から決定．
注意
結果1：EnKF
定理1
(Theorem 3.1 in T.2025arXivの改変)
注意
方程式と観測の組み合わせが重要．
\textstyle{\limsup_{n \rightarrow \infty}} \mathbb{E}[|v_n - u_n|^2] \le C r^2.
+いくつかの仮定
: Lorenz 96モデルの真の軌道（離散時間）
u_n (= u_{n\tau})
パラメータ で重みを制御 → 推定を観測に近づける．
(Filter accuracy)
v_n
: EnKFによる推定値
y_n \sim \mathcal{N}(Hu_n, r^2 I_{N_y})
: ノイズあり部分観測
このとき， について，
\tau \ll 1, \alpha \gg 0
\exists C = C(N_y, m, \tau, \alpha) \text{ s.t.}
\alpha \gg 0
(T.2025arXiv)
(\spadesuit)
似た結果は(SanzAlonso+2025)(Biswas+2024arXiv)．
は観測ノイズについての期待値
\mathbb{E}
2. アルゴリズム間の関係
観測条件の緩和（定理1）では，ノイズなし下での評価を応用．
問い：一般にできるか？
どう定式化されるか？
EnKFの や を制御して，連続時間同期フィルタに近い状況を再現．
\tau > 0
\alpha > 0
\alpha > 0
\tau > 0
\widehat{P}_n^{\alpha}
EnKF
同期
フィルタ
3DVar
連続時間
離散時間
ノイズあり
ノイズなし
時間依存重み
固定重み
重み 1
同期
フィルタ
観測頻度
観測ノイズ
✓
✓
①
②
③
④
基本はこれを
解析したい
アルゴリズム②
\frac{du_t}{dt}=\mathcal{F}(u_t), \quad t > 0
y_n = H u_{n\tau}, \quad n \in \mathbb{N}
\mathcal{Y} \subset \mathcal{X},
観測空間
（離散時間）同期フィルタ
P = H^* H, Q = I - P
p_n = y_n, \quad v_n^{-} = \Psi_{\tau}(v_{n-1})
真の時系列
観測
データ同化アルゴリズム
H \in \mathcal{L}(\mathcal{X}, \mathcal{Y}),
部分等長
v_n= p_n + q_n = p_n + Qv_{n}^{-} \in \operatorname{ran}(P) \oplus \operatorname{ran}(Q).
→ 推定値
射影
\tau > 0
観測間隔
離散時間ノイズなし
\mathcal{X}
Hilbert空間 上の発展方程式
離散時間で同期（不連続）
u_0 \in \mathcal{X}
\Psi_t
解作用素
( 時間発展)
t
※ノイズあり観測にも適用可能
観測空間
\oplus
未観測空間
アルゴリズム②
y_n
（離散時間）同期フィルタ
P = H^* H, Q = I - P
p_n = y_n, \quad v_n^{-} = \Psi_{\tau}(v_{n-1})
データ同化アルゴリズム
v_n= p_n + q_n = p_n + Qv_{n}^{-} \in \operatorname{ran}(P) \oplus \operatorname{ran}(Q).
→ 推定値
= y_n + Q\Psi_\tau(v_{n-1}) \in \operatorname{ran}(P) \oplus \operatorname{ran}(Q).
射影
\tau > 0
観測間隔
離散時間ノイズなし
離散時間で同期（不連続）
※ノイズあり観測にも適用可能
観測空間
\oplus
未観測空間
このように書ける．
アルゴリズム③
3次元変分法(3DVar)
データ同化アルゴリズム
推定値
y_n = H u_{n\tau} + \xi_n, \quad n \in \mathbb{N}
\mathcal{Y} \subset \mathcal{X},
観測空間
観測
H \in \mathcal{L}(\mathcal{X}, \mathcal{Y}),
部分等長
\tau > 0
観測間隔
離散時間ノイズあり
\frac{du_t}{dt}=\mathcal{F}(u_t), \quad t > 0
真の時系列
\mathcal{X}
Hilbert空間 上の発展方程式
u_0 \in \mathcal{X}
\Psi_t
解作用素
( 時間発展)
t
v_n = \text{重み付き平均}(\Psi_\tau(v_{n-1}), y_n; \widehat{P}^{\alpha})
\widehat{P}^{\alpha} = \alpha^2 I
重みは共分散 に依存．
チューニングパラメータ
\alpha
①ランダムノイズ
②有界ノイズ
\sim \mathcal{N}(0, r^2 I_{N_y})
|\xi_n| \le \epsilon
アルゴリズム③
3次元変分法(3DVar)
データ同化アルゴリズム
推定値
y_n
\tau > 0
観測間隔
離散時間ノイズあり
v_n = \text{重み付き平均}(\Psi_\tau(v_{n-1}), y_n; \widehat{P}^{\alpha})
チューニングパラメータ
\alpha
= \left(\frac{1}{1+\eta}P + Q\right)\Psi_\tau(v_{n-1}) + \frac{\eta}{1+\eta} y_n, \ \eta = \frac{\alpha^2}{r^2}
重みは共分散 に依存．
※一般には正定値行列
\widehat{P}^{\alpha} = \alpha^2 I
\widehat{P} = B.
時間依存しない重み．同期フィルタを「正則化」したような形．
注意
\rightarrow Q \Psi_\tau(v_{n-1}) + y_n \quad (\alpha \rightarrow \infty)
同期フィルタ！
離散時間フィルタ
定義
f: \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{X}
\exists L \in (0, 1) \text{ s.t.}
が離散時間フィルタであるとは
を満たすことをいう．
|f(x,y) - f(x',y)| \le L|x-x'|, \quad \forall x, x' \in \mathcal{X}, y \in \mathcal{Y}.
連続関数
注意
推定値 と観測 から次の推定値 を与える．
v_{n-1}
y_n
f(v_{n-1}, y_n)
同じ観測で更新すると異なる推定値が近づく．
（離散時間フィルタの更新写像）
|{}\cdot{}|
は のノルム．
X
結果2：更新写像と時系列の収束
定理2
(T.)
このとき，
\lim_{p \rightarrow \infty} \limsup_{n \rightarrow \infty} |v_n - v_n^p| = 0.
仮定：あるコンパクト集合 について
K \subset X \times Y
\textstyle{\sup_{(x,y) \in K}} |f(x,y) - f_p(x,y)| \le \delta_p \rightarrow 0 \ (p \rightarrow \infty),
(v_n^p, y_n) \in K, \ \forall n \in \mathbb{N}, p > 0.
近似
(2)
(1)
v_n^p
: 別の離散時間フィルタによる推定値
v_n = f(v_{n-1}, y_n)
v_n^p = f_p(v_{n-1}^p, y_n)
v_n
: ある離散時間フィルタによる推定値
y_n
：観測列
\subset Y
|{}\cdot{}|
は のノルム．
X
注意
証明はフィルタの縮小性と仮定(1)による．
結果2：推定値の近似
系1
(T.)
注意
3DVar → 同期フィルタ
v_n = f(v_{n-1}, y_n)
v_n^{\alpha} = f_\alpha(v_{n-1}^\alpha, y_n)
\lim_{\alpha \rightarrow \infty} \limsup_{n \rightarrow \infty} |v_n - v_n^\alpha| = 0.
(\spadesuit)
y_n
：Lorenz 96モデルに対する有界ノイズありの観測
v_n
: 同期フィルタによる推定値
Lorenz96モデルに同期フィルタと3DVarを適用．
v_n^{\alpha}
: 3DVarによる推定値
EnKF → 3DVarの近似もできそう．
より単純なアルゴリズムでの解析に帰着できる．
このアプローチの課題
誤差
観測ノイズ
のレベル
\alpha
紹介した理論は
この状況を解析
応用上は
この辺りが重要
パラメータ とEnKFの誤差の関係について（現状の理解）
\alpha
より単純なアルゴリズムに近づけるため，
応用上重要な状況の解析にはなっていない可能性がある．
3. 離散化誤差の考慮
これまでの議論では，モデルの時間発展 が厳密に解けることを前提にしていた．
\Psi_t
→ 基本的にモデルはわからない．数値計算上は離散化誤差などが含まれる．
c. 観測誤差に含めるという考えもある．
a. SDEでモデルノイズとして考慮（よくある．）
dX_t = f(X_t)dt + \sigma(X_t) dW_t
b. Surrogate modelとして考慮（SanzAlonso+2025)
|\Psi_t(x) - \Psi_t^s(x)| \le \epsilon_s
対応
これに注目
→これと同じ方針
アルゴリズム②'
\frac{du_t}{dt}=\mathcal{F}(u_t), \quad t > 0
y_n = H u_{n\tau}, \quad n \in \mathbb{N}
\mathcal{Y} \subset \mathcal{X},
観測空間
（離散時間）同期フィルタ
P = H^* H, Q = I - P
p_n = y_n, \quad v_n^{-} = \Psi_{\tau, \Delta t}(v_{n-1})
真の時系列
観測
データ同化アルゴリズム
H \in \mathcal{L}(\mathcal{X}, \mathcal{Y}),
有界線形
v_t = p_n + q_n = p_n + Qv_{n}^{-} \in \operatorname{ran}(P) \oplus \operatorname{ran}(Q).
→ 推定値
射影
\tau > 0
観測間隔
離散時間ノイズなし
\mathcal{X}
Hilbert空間 上の発展方程式
離散時間で同期（不連続）
u_0 \in \mathcal{X}
\Psi_t
解作用素
( 時間発展)
t
Δtで時間離散化
Δtで時間離散化
結果3：離散化誤差あり同期フィルタ
定理
(T.)
注意
|Q(\Psi_\tau(u) - \Psi_\tau(u'))| \le \theta_\tau |u - u'|, \ \forall u, u' \in \mathcal{X}.
|Q(\Psi_\tau(u) - \Psi_{\tau, \Delta t}(u))| \le C_\tau (\Delta t)^k, \ \forall u \in \mathcal{X}.
仮定
離散化誤差
時間離散化に限定
このとき，
\limsup_{n\rightarrow \infty}|v_n - u_n| \le \frac{C_\tau}{1 - \theta_\tau} (\Delta t)^k.
\exists \theta_\tau \in (0, 1) \text{ s.t.}
\exists C_\tau > 0, k \in \mathbb{N} \text{ s.t.}
未観測空間での縮小性
Lorenz 96モデルは仮定1を満たす．
適当な数値積分スキーム仮定2が成り立つ
(1)
(2)
まとめ：データ同化と定式化
時系列データ同化 → 時系列観測を予測値に重みつきで混ぜる．
ある観点からは．．．
定理1（部分観測でFilter accuracy）
定理2 & 系1
定理3（離散化誤差評価）
\approx
同期
フィルタ
3DVar
連続時間
離散時間
ノイズなし
固定重み
重み 1
同期
フィルタ
観測頻度
観測ノイズ
EnKF
時間依存重み
ノイズあり
\approx
①
②
③
④
基本はこれを
解析したい
これから
結果1（部分観測とFilter accuracy）
結果2（アルゴリズム間の関係）
定理2により，定理1の別証明ができるかも．
系1
\approx
3DVar
同期フィルタ
EnKF
\approx
TODO
結果3（モデル誤差の考慮）
定理3について数値実験で検証する．
(SanzAlonso+2025)は一般のSurrogateモデルについて評価．
→ 機械学習モデルの事後誤差評価があれば数値検証できる．
定理1において，位相の改善等について議論．
②
③
④
参考文献
- (T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
- (T. 2025) Kota Takeda, Error Analysis of the Ensemble Square Root Filter for Dissipative Dynamical Systems, PhD Thesis, Kyoto University, 2025.
- (Kelly+2014) D. T. B. Kelly, K. J. H. Law, and A. M. Stuart (2014), Well-posedness and accuracy of the ensemble Kalman filter in discrete and continuous time, Nonlinearity, 27, pp. 2579–260.
- (Al-Ghattas+2024) O. Al-Ghattas and D. Sanz-Alonso (2024), Non-asymptotic analysis of ensemble Kalman updates: Effective dimension and localization, Information and Inference: A Journal of the IMA, 13.
- (Tong+2016a) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability and ergodicity of ensemble based Kalman filters, Nonlinearity, 29, pp. 657–691.
- (Tong+2016b) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability of the ensemble Kalman filter with adaptive covariance inflation, Comm. Math. Sci., 14, pp. 1283–1313.
- (Kwiatkowski+2015) E. Kwiatkowski and J. Mandel (2015), Convergence of the square root ensemble Kalman filter in the large ensemble limit, Siam-Asa J. Uncertain. Quantif., 3, pp. 1–17.
- (Mandel+2011) J. Mandel, L. Cobb, and J. D. Beezley (2011), On the convergence of the ensemble Kalman filter, Appl.739 Math., 56, pp. 533–541.
参考文献
-
(de Wiljes+2018) J. de Wiljes, S. Reich, and W. Stannat (2018), Long-Time Stability and Accuracy of the Ensemble Kalman-Bucy Filter for Fully Observed Processes and Small Measurement Noise, Siam J. Appl. Dyn. Syst., 17, pp. 1152–1181.
-
(Burgers+1998) G. Burgers, P. J. van Leeuwen, and G. Evensen (1998), Analysis Scheme in the Ensemble Kalman Filter, Mon. Weather Rev., 126, 1719–1724.
-
(Bishop+2001) C. H. Bishop, B. J. Etherton, and S. J. Majumdar (2001), Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects, Mon. Weather Rev., 129, 420–436.
-
(Anderson 2001) J. L. Anderson (2001), An Ensemble Adjustment Kalman Filter for Data Assimilation, Mon. Weather Rev., 129, 2884–2903.
-
(Dieci+1999) L. Dieci and T. Eirola (1999), On smooth decompositions of matrices, Siam J. Matrix Anal. Appl., 20, pp. 800–819.
-
(Reich+2015) S. Reich and C. Cotter (2015), Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge University Press, Cambridge.
-
(Law+2015) K. J. H. Law, A. M. Stuart, and K. C. Zygalakis (2015), Data Assimilation: A Mathematical Introduction, Springer.
参考文献
-
(Law+2016) K. J. H. Law et al., Filter accuracy for the Lorenz 96 model: Fixed versus adaptive observation operators, Phys. Nonlinear Phenom., 325, 1–13.
-
(Azouani+2014) A. Azouani, E. Olson, and E. S. Titi, Continuous Data Assimilation Using General Interpolant Observables, J. Nonlinear Sci., 24, 277–304.
-
(Hayden+2011) K. Hayden, E. Olson, and E. S. Titi, Discrete data assimilation in the Lorenz and 2D Navier-Stokes equations, Phys. -Nonlinear Phenom., 240, pp. 1416– 1425.
-
(Sanz-Alonso+2025), Sanz-Alonso, D., Waniorek, N., 2025. Long-Time Accuracy of Ensemble Kalman Filters for Chaotic Dynamical Systems and Machine-Learned Dynamical Systems. SIAM J. Appl. Dyn. Syst. 2246–2286. https://doi.org/10.1137/24M1719232.
-
(Biswas+2024), https://arxiv.org/abs/2402.14078.
-
(T.2025) K. T., Error analysis of the projected PO method with additive inflation for the partially observed Lorenz 96 model, arXiv preprint, https://doi.org/10.48550/arXiv.2507.23199.
データ同化における推定誤差解析の現状と課題
By kotatakeda
データ同化における推定誤差解析の現状と課題
RIMS共同研究 (公開型) 数値解析が切り開く新たな情報社会 〜データ駆動型から「富岳NEXT」〜，京都大学, 2025/10/8-10.
