Politics through the Lens of Economics
Lecture 14: War
Masayuki Kudamatsu
17 January, 2018
Discussion Time
For your term paper...
Does the legislative bargaining model explain
Why won't the Japanese government discourage
Simultaneous recruiting
of new graduates (新卒一括採用)
in the 21st century?
Background for discussion
Until 2010, Japan and South Korea
were the only countries with the practice of 新卒一括採用
According to Wikipedia (so it has to be double-checked...)
In 2010, South Korea
banned any form of age discrimination in hiring
which discouraged(?) 新卒一括採用
Background for discussion
In 2007, Council on Economic and Fiscal Policy (経済財政諮問会議)
proposed to abolish 新卒一括採用(「労働ビッグバン」)
But both managers and labor unions opposed it
Discussion Time
For your term paper...
Does the legislative bargaining model explain
Why won't the Japanese government discourage
Simultaneous recruiting
of new graduates (新卒一括採用)
in the 21st century?
Motivation: Why do we fight a war?
Since 1945, interstate wars
have become less frequent
But civil wars
have been widespread
# of years of conflict
If we plot...
During 1960-2006
% of countries
with 1000+ deaths
per year
due to conflicts
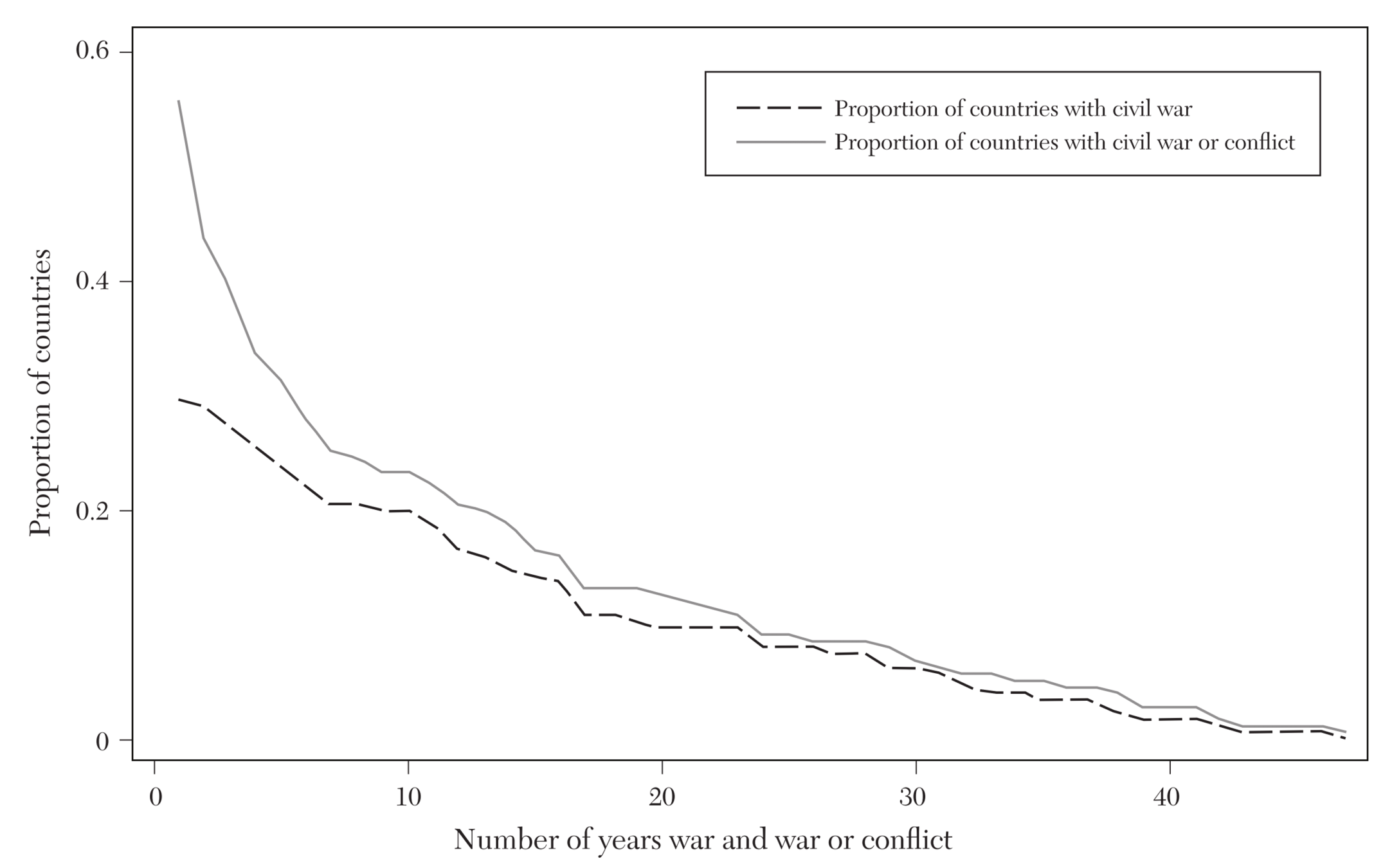
Countries with 1000+ deaths per year
Countries with 25+ deaths per year
Image source: Figure 1 of Blattman and Miguel (2010)
Data source: Armed Conflict Database
In 2017
the following countries
had more than 3000 deaths per year due to civil wars
Afghanistan
Iraq
Libya
Mexico
Nigeria
Somalia
South Sudan
Syria
Yemen
Source: Armed Conflict Database
Today's Road Map

Contest Model
Commitment Model
Evidence from Colombia
Does poverty intensify wars?
Today's Road Map

Contest Model
Commitment Model
Evidence from Colombia
Why can't peaceful solutions be feasible?
Today's Road Map

Contest Model
Commitment Model
Evidence from Colombia
Players
Two groups of people in conflict
Each simultaneously allocates their time
between production & fighting
Benefits from production
Benefits from fighting
Wages
Prize from winning the war
Agricultural yields
Profits (for firm managers)
e.g.
Political power
Mineral export revenue
e.g.
National army & Rebels
Players' action
That's the model.
To understand the optimal level of fighting for each group
we need to figure out, as usual, two things:
Extra benefit & cost
from additional fighting time
Extra benefit
Winning probability
doesn't go up much
if you have spent a lot
Fighting hours
Extra benefit from fighting time
Extra benefit
Extra benefit goes up if
Extra benefit from fighting time (cont.)
Fighting hours
The winning prize
is higher
The opponent
fights longer
or
Extra cost from fighting time
Extra cost
Wage per hour
Fighting hours
Extra cost from fighting time (cont.)
Extra cost
Wage per hour
Fighting hours
Recession reduces extra cost of fighting
Optimal fighting hours
Extra
Benefit / Cost
Wage per hour
Fighting hours
Optimal level
If the winning prize becomes more valuable...
Extra
Benefit / Cost
Wage per hour
Fighting hours
Fight
more
If hourly wage goes down...
Extra
Benefit / Cost
Wage per hour
Fighting hours
Fight
more
Poverty intensifies fighting
So far we considered each group's optimal behavior
But one group's behavior affects the other group's
e.g.
If you get attacked, you fight back
We need to find the equilibrium
If the enemy fights more...
Extra
Benefit / Cost
Wage per hour
Fighting hours
Fight
more
Your
fighting hours
Enemy's fighting hours
If the enemy fights more, you fight more
Your
fighting hours
Enemy's fighting hours
If you fight more, your enemy fights more
Your
fighting hours
Enemy's fighting hours
Fighting escalates...
Your
fighting hours
Enemy's fighting hours
Fighting escalates...
Your
fighting hours
Enemy's fighting hours
Fighting escalates...
Your
fighting hours
Enemy's fighting hours
Fighting escalates...
Your
fighting hours
Enemy's fighting hours
Fighting escalates until it reaches an equilibrium
Now consider how the equilibrium behavior changes
when one of the groups is impoverished
If hourly wage goes down...
Extra
Benefit / Cost
Wage per hour
Fighting hours
Fight
more
Remember:
Your
fighting hours
Enemy's fighting hours
If the enemy's wage goes down, they fight more
Your
fighting hours
Enemy's fighting hours
In equilibrium, both sides fight more
Poverty for one side
escalates fighting on both sides
Summary
Poverty
You don't earn much by working
Fighting is relatively more attractive
More
intensified
conflicts
The opponent is fighting back
Evidence from Colombia
Civil wars in Colombia (since 1960s)
Communist guerrillas
Paramilitary groups
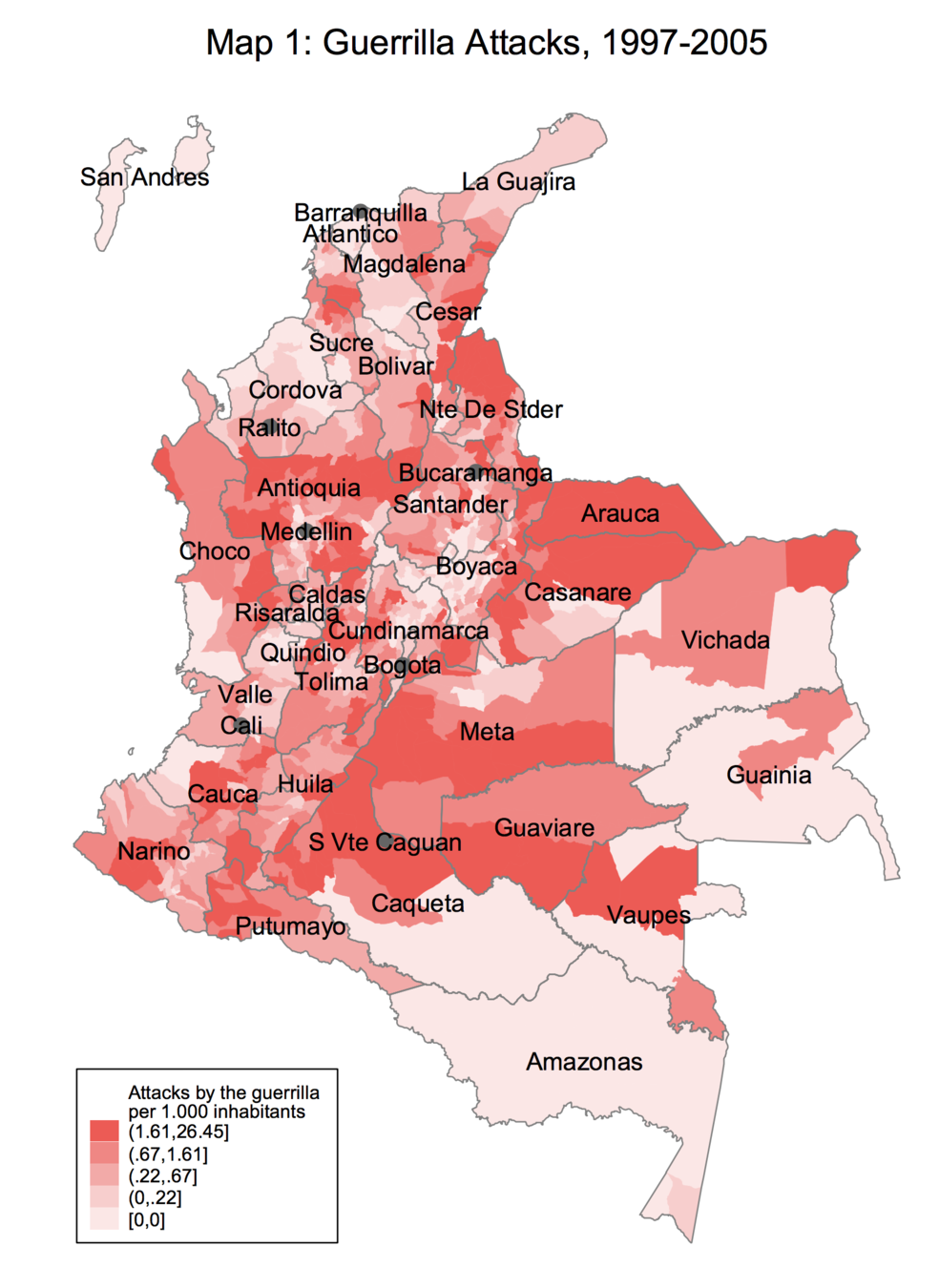
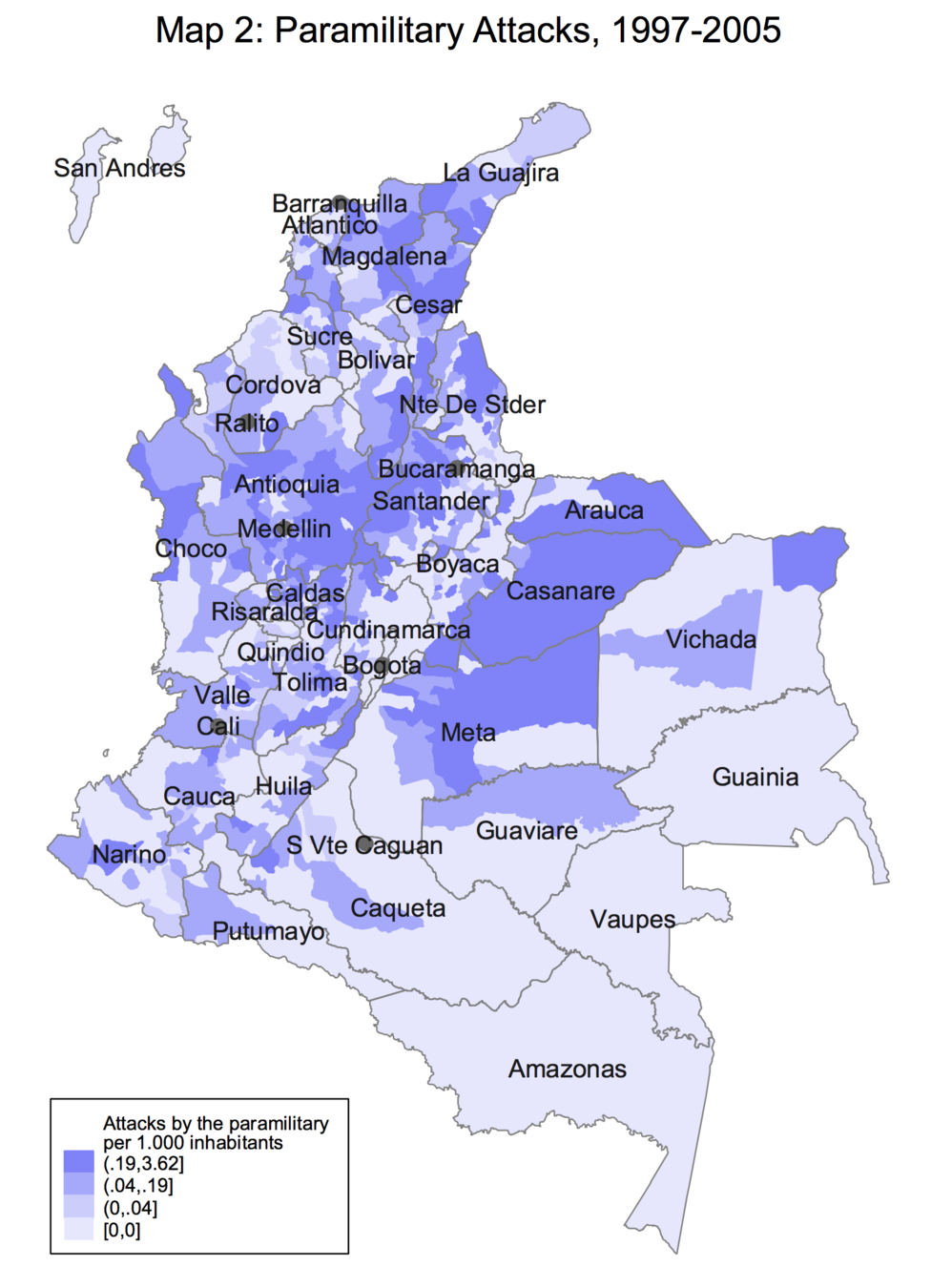
Source: Acemoglu et al. (2009)
Testing whether lower wage intensifies conflict
Colombia: among top 3 coffee exporters
In coffee-producing areas in Colombia, then
Lower world coffee prices = Lower wages for coffee farmers
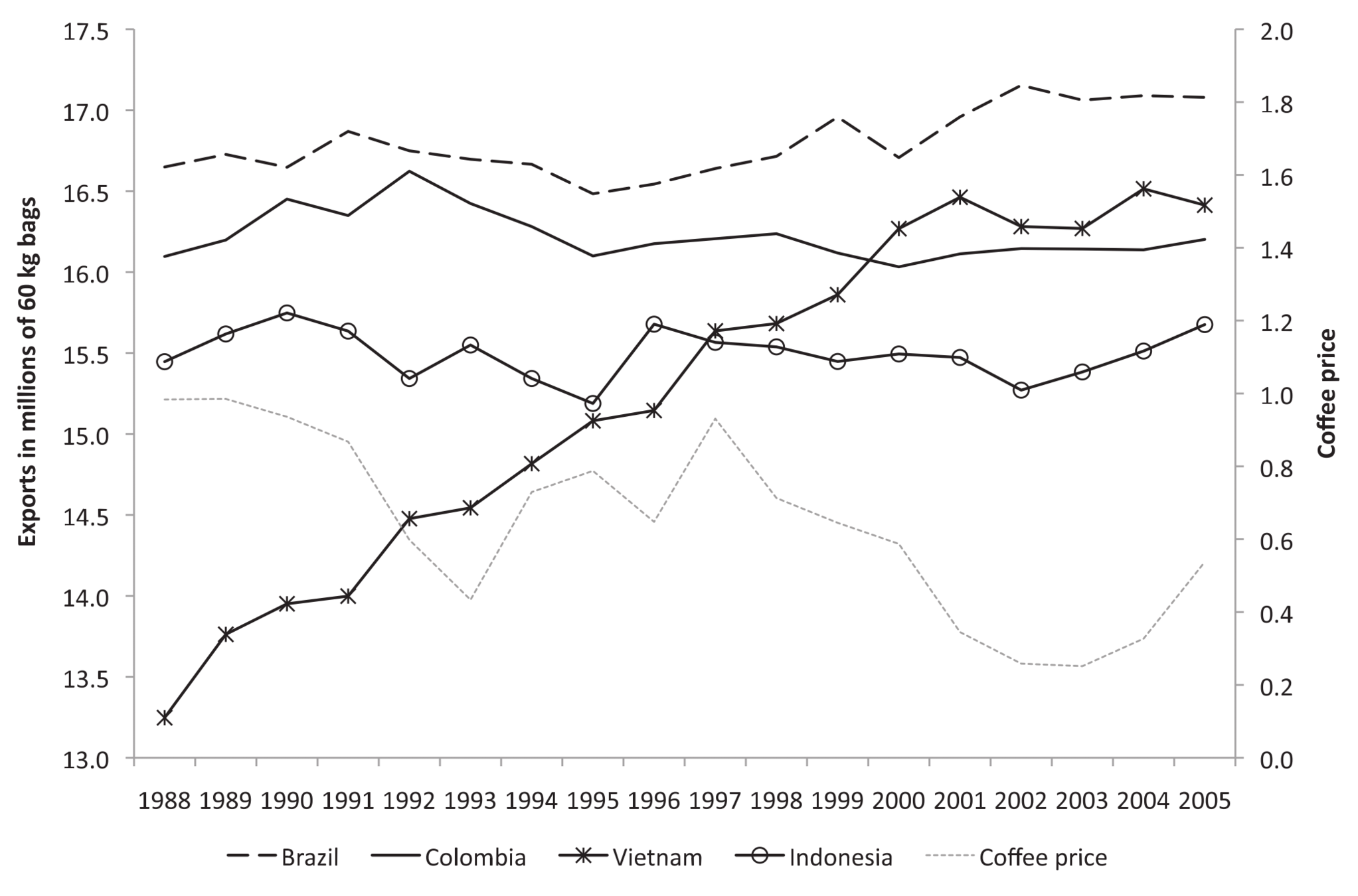
Source: Figure 2 of Dube and Vargas (2013)
Data
For each of 978 municipalities:
# of guerrilla attacks
# of paramilitary attacks
# of clashes between the two sides
# of casualities
in each year between 1988 and 2005
Amount of land for coffee cultivation in 1997
For each year between 1988 and 2005
World prices of coffee
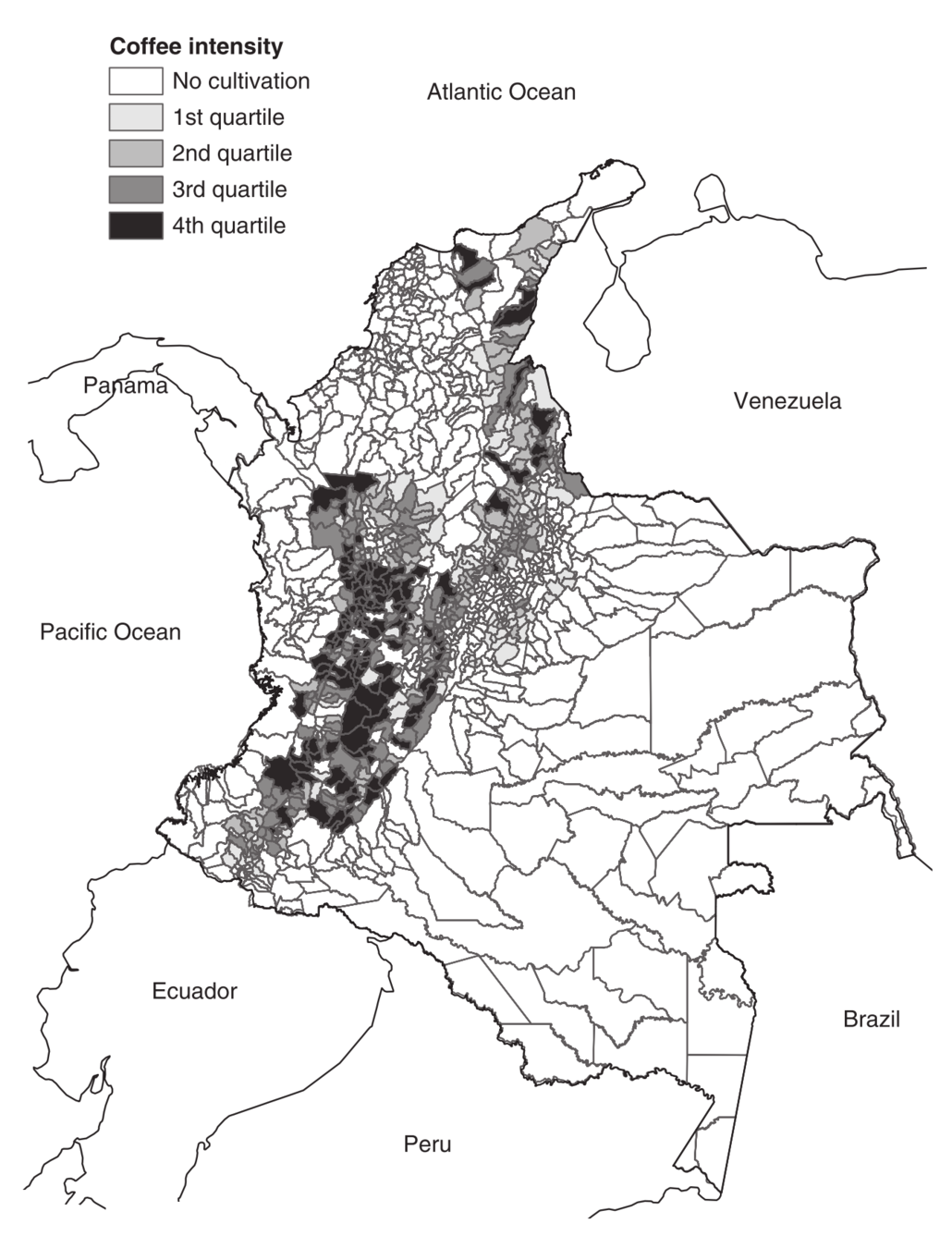
Coffee-growing
municipalities
of Colombia
Source: Figure 1A of Dube and Vargas (2013)
Estimation strategy: Difference-in-differences
| Years of low coffee prices | Years of high coffee prices | |
| Coffee producing municipalities |
A |
B |
|
Others |
C |
D |
Impact of low wage on conflict
= (A - B) - (C - D)
Conflict intensifies more in coffee areas
when world coffee price drops
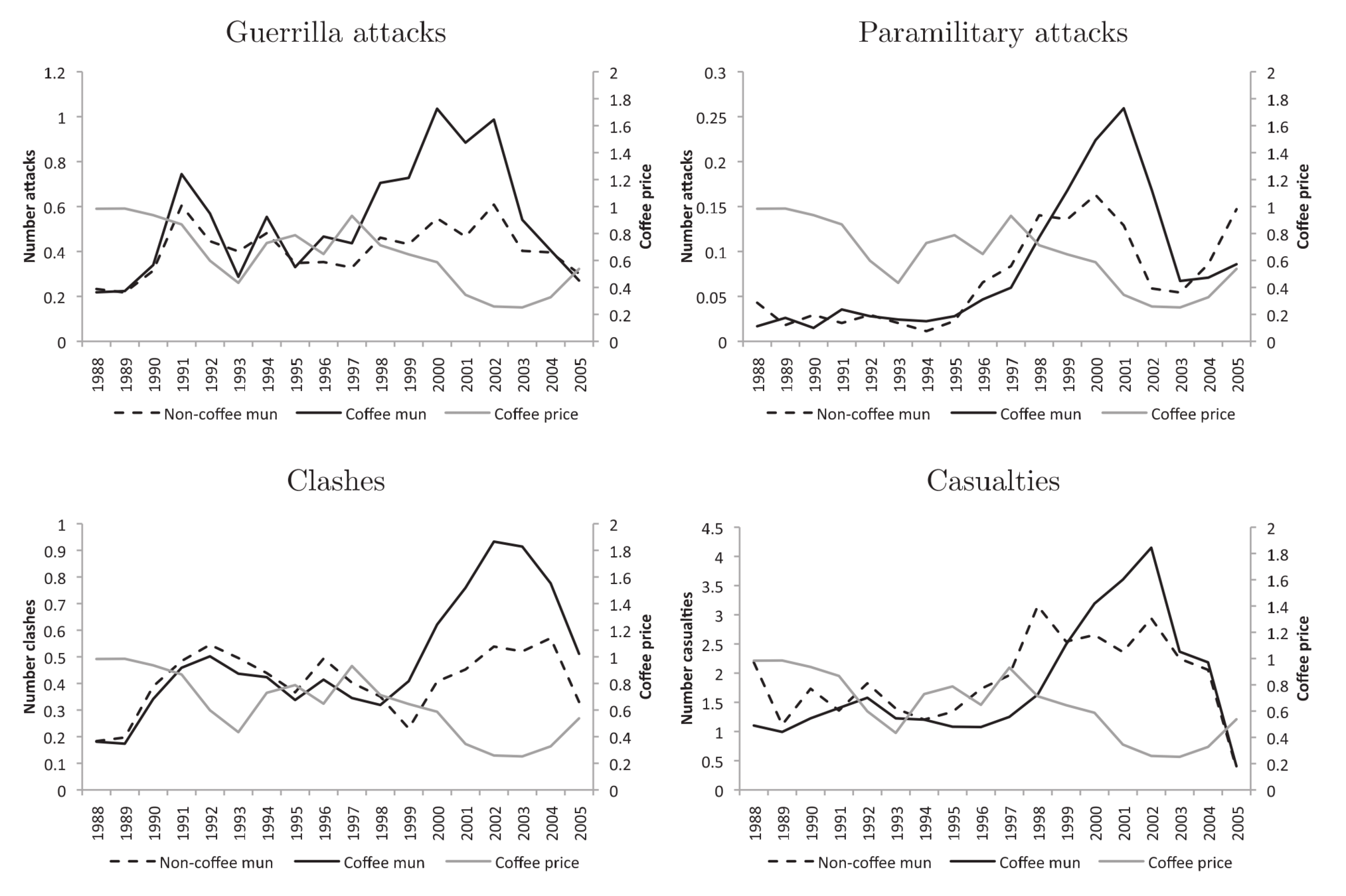
Source: Figure 4 of Dube and Vargas (2013)
By how much?
Coffee price dropped by 68% from 1997 to 2003
The rise in conflict is larger for coffee areas than for the rest
by 18% - 31% of the average level
Source: p. 1403 of Dube and Vargas (2013)
Today's Road Map

Contest Model
Commitment Model
Evidence from Colombia
The contest model explains what intensifies a war
If the two parties agree to split the winning prize
both are better off
Because then both parties work full-time to earn wage
The commitment model explains when a war cannot be avoided
but doesn't explain why a war cannot be avoided
Imagine...
Two parties, A & B, cannot agree on something
e.g.
North Korea
Wants to continue their nuclear weapon development
U.S.
Wants to stop it
We now model the process of negotiation
Timing of Events
1
Party A decides whether to compromise
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
Timing of Events
1
Party A decides whether to compromise
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
2
Party B decides whether to stage a war
Suppose it's optimal for B to stage a war
if and only if A doesn't compromise
How peace can be achieved in this model
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
How peace can be achieved in this model (cont.)
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
Then it's optimal for A
to compromise when the war is more costly
However, there is always tomorrow.
A
Compromise
Doesn't
War
B
B
War
Peace
Extend the model
to a two-period one
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
Extend the model
to a two-period one
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
Does B still choose peace in period 1 ?
A
Compromise
Doesn't
War
B
B
War
Peace
Suppose in next period it's optimal for B
not to stage a war even if A doesn't compromise
e.g.
Skillful military leaders die
More difficult to recruit solidiers due to the economic boom
How peace cannot be achieved
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
How peace cannot be achieved (cont.)
Peace
Then it's optimal for A
not to compromise when the war is more costly
e.g.
North Korea kept their nuclear weapon development
as they didn't believe that U.S. will otherwise attack them
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
If B anticipates that A won't compromise in the next period
what should B do today?
Compromise
Doesn't
War
Peace
B
B
War
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
It can be optimal
for B to go to war
even if
A compromises.
A
Compromise
Doesn't
War
Peace
B
B
War
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
A
B may be militarily weaker
in next period
Compromise
Doesn't
War
Peace
B
B
War
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
A
Then, A cannot commit
to compromise
in next period
Compromise
Doesn't
War
Peace
B
B
War
Peace
A
Compromise
Doesn't
War
B
B
War
Peace
A
Anticipating this
B prefers a war while
they are militarily strong
A's lack of commitment to future compromise
makes a costly war unavoidable
Evidence?
Not available (yet)
Difficult to measure
the anticipated changes
in military strength
Next week...
Term paper workshop !
Pick one model that is likely to explain the policy of your choice
Provide facts and evidence in favor of (or against) your argument
Also see Term Paper Guideline
Each of you have 8 minutes including discussions
Next week...
Term paper workshop !
Pick one model that is likely to explain the policy of your choice
Provide facts and evidence in favor of (or against) your argument
Also see Term Paper Guideline
Each of you have 8 minutes including discussions
Aim: Come up with a wrong answer

For Term Paper Workshop
This lecture is based on the following academic articles:
Commitment Model
Garfinkel, Michelle R., and Stergios Skaperdas. 2006. "Economics of Conflict: An Overview." in Sandler, T., and K. Hartley (Eds.), Handbook of Defense Economics. Elsevier, pp. 649–709.
Contest Model
Evidence from Colombia
Dube, O., and J.F. Vargas. 2013. "Commodity Price Shocks and Civil Conflict: Evidence from Colombia." The Review of Economic Studies, 80(4): 1384–1421.
Powell, Robert. 2006. "War as a Commitment Problem." International Organization, 60 169–203.
Politics through the Lens of Economics: Lecture 14 War
By Masayuki Kudamatsu
Politics through the Lens of Economics: Lecture 14 War
- 1,718



