{資料結構}

Data Structure

資料結構是電腦組織資料的結構

不同組織資料的方式，有不同的效果

如果能在適當的時機使用適當的資料結構

就能有效提升算法的效率

例如 :

dijkstra 演算法使用 min heap

kruskal 演算法使用 DSU

BFS 演算法使用 queue

例如 :

dijkstra 演算法使用 min heap

kruskal 演算法使用 DSU

BFS 演算法使用 queue

其實你已經超會用了 !

ex : 平常使用的 set、map 甚至陣列

{前綴和}

給定一個長度為n的序列A

假設你要做出一個機器，可以執行以下操作:

詢問第 l ~ r 項的和

總共有 q 個操作要處理

如果直接硬做?

每次詢問，就用迴圈將 l~r 掃過並加總

如果直接硬做?

每次詢問，就用迴圈將 l~r 掃過並加總

時間複雜度 : 

O(nq)

可能可以事先對陣列做一些事情

讓接下來的處理變快?

我們發現如果要求 l ~ r 的區間和

其實可以這樣算 :

\sum_{i=1}^{r}a_i - \sum_{i=1}^{l-1}a_i

我們發現如果要求 l ~ r 的區間和

其實可以這樣算 :

\sum_{i=1}^{r}a_i - \sum_{i=1}^{l-1}a_i

因此我們定義一個新的陣列 pre

pre_i = \sum_{j=1}^{i}a_j

一但我們算出 pre 陣列後

之後的查詢就變得超簡單!

sum(l,r) = pre_r-pre_{l-1}

一但我們算出 pre 陣列後

之後的查詢就變得超簡單!

sum(l,r) = pre_r-pre_{l-1}

單次詢問時間複雜度直接變成 const

要算出 pre 陣列其實也很簡單!

可以發現 :

pre_i = pre_{i-1}+a_i

因此預處理的時間複雜度為

O(n)

總時間複雜度

O(n+q)
#include<bits/stdc++.h>
using namespace std;
#define maxn 200005

int n,q,arr[maxn],pre[maxn];

main(){
    cin>>n>>q;
    for(int i=1;i<=n;++i) cin>>arr[i];
    for(int i=1;i<=n;++i) pre[i] = pre[i-1]+arr[i];

    for(int i=1;i<=q;++i){
        int l,r; cin>>l>>r;
        cout<<pre[r]-pre[l-1]<<endl;
    }
}
# PRESENTING CODE

範例 code 、模板練習題

如果變成二維的呢?

有一個 n*n 的網格，每格有一個數字

我們表示第 i 橫列，第 j 直行為

a_{i,j}

每次詢問 

(x_1,y_1)、(x_2,y_2)

圍出的矩形的元素總和

(x_1,y_1)
(x_2,y_2)

要求的就是橘色框框中的所有數字和

我們依樣利用前綴和的蓋念，但這次定義有點不同

我們定義                 為包含這格，以及其左上所有元素的和

pre_{i,j}

我們如何利用 pre 還求出一個矩形的和呢?

我們要求出

橘色矩形中的和

我們如何利用 pre 還求出一個矩形的和呢?

我們要求出

橘色矩形中的和

A

A

我們如何利用 pre 還求出一個矩形的和呢?

我們要求出

橘色矩形中的和

B

A-B

我們如何利用 pre 還求出一個矩形的和呢?

我們要求出

橘色矩形中的和

C

A-B-C

我們如何利用 pre 還求出一個矩形的和呢?

我們要求出

橘色矩形中的和

D

A-B-C+D

我們如何利用 pre 還求出一個矩形的和呢?

我們要求出

橘色矩形中的和

A-B-C+D

將這四個區域做一些運算

就可以得到答案了!

我們如何利用 pre 還求出一個矩形的和呢?

我們要求出

橘色矩形中的和

A-B-C+D

將這四個區域做一些運算

就可以得到答案了!

並且ABCD都是

pre中有的!

寫的更嚴謹就是:

(x_1,y_1)
(x_2,y_2)
sum(x_1,y_1,x_2,y_2) =
pre_{x_2,y_2}-pre_{x_1-1,y_2}-pre_{x_2,y_1-1}+ pre_{x_1-1,y_1-1}
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define maxn 505

int arr[maxn][maxn],n,m,q,pre[maxn][maxn];

int query(int a,int b,int x,int y){
    return pre[x][y] + pre[a-1][b-1] - pre[x][b-1] - pre[a-1][y];
}
main(){
    cin>>n>>m>>q;
    for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) cin>>arr[i][j];
    for(int i=1;i<=n;++i) for(int j=1;j<=m;++j)
        pre[i][j] = pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+arr[i][j];
    while(q--){
        int a,b,x,y; cin>>a>>b>>x>>y;
        a++,b++,x++,y++;
        cout<<query(a,b,x,y)<<endl;
    }
}
# PRESENTING CODE

範例 code 、模板練習題

{差分}

給定一個長度為n的序列 A

假設你要做出一個機器，可以執行以下操作:

將 l ~ r 項全部個別加上 x

等待 q 筆操作完成後，輸出每一項的數值

如果直接硬做?

每次操作，就用迴圈將 l~r 掃過並每項加值

最後輸出陣列即為答案

如果直接硬做?

每次操作，就用迴圈將 l~r 掃過並每項加值

最後輸出陣列即為答案

時間複雜度為

O(nq)

我們可以構造一個新的定義

讓他可以快速支援區間修改操作

我們可以構造一個新的定義

讓他可以快速支援區間修改操作

定義:

D_i = a_i - a_{i-1}

也就是紀錄相鄰兩項的差

當我們把陣列 A 變成 D 後

可以發現區間加值變超容易 !

當我們要將區間 ( l , r ) 加值 x 

等同於 :

D_l + x
D_{r+1} - x

當我們把陣列 A 變成 D 後

可以發現區間加值變超容易 !

當我們要將區間 ( l , r ) 加值 x 

等同於 :

D_l + x
D_{r+1} - x

可以發現修改這兩個地方

就可以維護好 D 的性質(依照定義)

接下來我要如何用 D 還原出答案呢?

我們可以發現，原陣列第 i 項其實就是 :

a_i = \sum_{j=1}^{i}D_j

接下來我要如何用 D 還原出答案呢?

我們可以發現，原陣列第 i 項其實就是 :

a_i = \sum_{j=1}^{i}D_j

可以理解成將從頭開始的變化量

全部加總，就會是這一項的值

a_i = \sum_{j=1}^{i}D_j

計算方式跟前綴和一樣

(D的前綴和陣列就是原陣列了 ! )

a_i = \sum_{j=1}^{i}D_j

計算方式跟前綴和一樣

(D的前綴和陣列就是原陣列了 ! )

總時間複雜度 :

O(q+n)
#include<bits/stdc++.h>
using namespace std;
#define maxn 200005

int n,q,arr[maxn],D[maxn],pre[maxn];

main(){
    cin>>n>>q;
    for(int i=1;i<=n;++i) cin>>arr[i];
    for(int i=1;i<=n;++i) D[i] = arr[i]-arr[i-1];
    for(int i=1;i<=q;++i){
        int l,r,x; cin>>l>>r>>x;
        D[l] += x;
        D[r+1] -= x;
    }
    for(int i=1;i<=n;++i) pre[i] = pre[i-1]+D[i];
    for(int i=1;i<=n;++i) cout<<pre[i]<<' ';
    cout<<endl;
}

# PRESENTING CODE

範例code

#include<bits/stdc++.h>
using namespace std;
int n,as,t;
vector<pair<int,int>> pv;
int main(){
    cin>>n;
    for(int i=0;i<n;++i){
        int a,b; cin>>a>>b;
        pv.push_back({a,1});
        pv.push_back({b+1,-1});
    }
    sort(pv.begin(),pv.end());
    for(auto it:pv){
        t += it.second;
        as = max(as,t);
    }
    cout<<as;
    return 0;
}

# PRESENTING CODE

練習題 

差分也可以二維 !

{樹狀樹組}

支援

單點修改，區間查詢

                 區間修改，單點查詢(套差分)

每次操作複雜度皆為

O(logn)

單點修改，查詢前綴合

首先我們介紹一個東西 : lowbit

lowbit(x) 代表 x 的二進位表示法中

最小為 1 的位數所代表的二的冪次

ex :

lowbit(12) = 4   <-  12 的二進位為 1100

lowbit(16) = 16   <-  16 的二進位為 10000

如何快速計算 lobit ?

非常簡單，lowbit(x) = x & (-x)

如何快速計算 lobit ?

非常簡單，lowbit(x) = x & (-x)

為什麼 ?

 x = 00010100

 -x =  11101011 + 00000001

= 11101100

x&(-x) = 00000100 

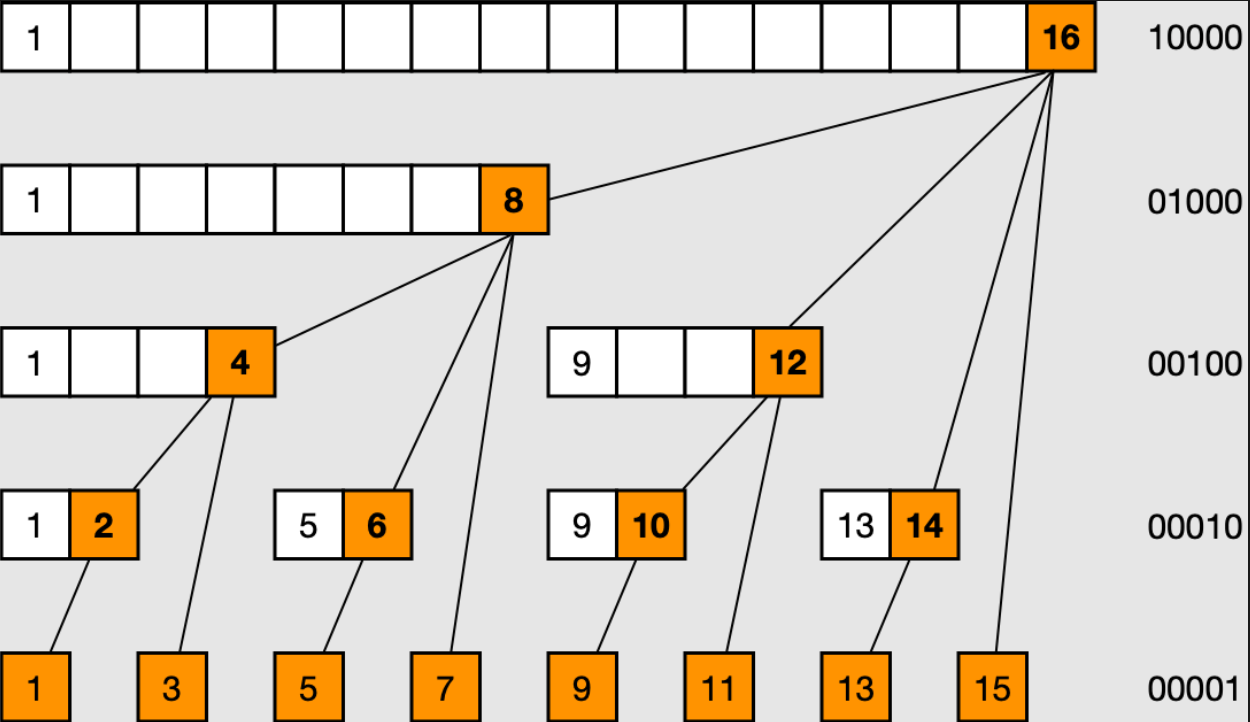
我們定義 :

BIT_i = \sum_{j=i-lowbit(i)+1}^{i} a_j

如何區間查詢前綴合?

lowbit : 

15  -> 1111 -> lowbit = 1

14 -> 1110 -> lowbit = 2

12 -> 1100 -> lowbit = 4

8 -> 1000 -> lowbit = 8

lowbit : 

15  -> 1111 -> lowbit = 1

14 -> 1110 -> lowbit = 2

12 -> 1100 -> lowbit = 4

8 -> 1000 -> lowbit = 8

前15項和 =

 

bit_{15} + bit_{14} + bit_{12} +bit_{8}

11 -> 1011 -> lowbit = 1

10 -> 1010 -> lowbit = 2

8 -> 1000 -> lowbit = 8

lowbit : 

11 -> 1011 -> lowbit = 1

10 -> 1010 -> lowbit = 2

8 -> 1000 -> lowbit = 8

lowbit : 

前11項和 =

 

bit_{11} + bit_{10} +bit_{8}

如何單點修改?

如果要單點修改，必須要改到所有包含他的地方

9  ->  01001 -> lowbit = 1

10 -> 01010 -> lowbit = 2

12 -> 01100 -> lowbit = 4

16 -> 10000 -> lowbit = 16

9  ->  01001 -> lowbit = 1

10 -> 01010 -> lowbit = 2

12 -> 01100 -> lowbit = 4

16 -> 10000 -> lowbit = 16

若要加值 9 

則我們要將 bit 的 9、10、12、16

全部都加值

可以發現我們單點修改、查尋前綴和

會用到的 bit 位置數量級只有

O(logn)

可以發現我們單點修改、查尋前綴和

會用到的 bit 位置數量級只有

O(logn)

因此兩個操作的時間複雜度都是 

O(logn)

可以發現我們單點修改、查尋前綴和

會用到的 bit 位置數量級只有

O(logn)

因此兩個操作的時間複雜度都是 

O(logn)

重點是，超好寫!

如果要支援

區間改值、單點查詢也很簡單

只需要用 bit 的原本功能 (單點改、查前綴和)

再套上差分就可以做到

#include<bits/stdc++.h>
using namespace std;
#define maxn 200005

int n,q,bit[maxn];

int lb(int x){
    return x&(-x);
}
void modify(int x,int v){
    for(int i=x;i<maxn;i+=lb(i)) bit[i] += v;
}
int query(int x){
    int sum = 0;
    for(int i=x;i;i-=lb(i)) sum += bit[i];
    return sum;
}
# PRESENTING CODE

範例 code

# PRESENTING CODE

範例 code

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define maxn 200005
LL bit[maxn];
LL n,q;
LL lb(LL x){
    return x&(-x);
}
void modify(LL x,LL v){
    for(int i=x;i<=n;i+=lb(i)){
        bit[i] += v;
    }
}
LL query(LL x){
    LL sm=0;
    for(int i=x;i>0;i-=lb(i)){
        sm+=bit[i];
    }
    return sm;
}
int main(){
    cin>>n>>q;
    for(int i=1;i<=n;++i){
        LL a;cin>>a;
        modify(i,a);
    }
    while(q--){
        LL a,b,c;cin>>a>>b>>c;
        if(a==1) modify(b,c-(query(b)-query(b-1)));
        else cout<<query(max(b,c))-query(min(b,c)-1)<<endl;
    }
    return 0;
}

{基礎線段樹}

線段樹是一個非強強大

處理區間問題的工具

這裡會介紹其最基本的型態

線段樹可以支援一些對區間的修改、查詢操作

核心概念就是將資料分段存起來，要用的時候再將不同片段合併得到答案

怎們切資料呢 ?

以下我們先以區間最大值為例

怎們切資料呢 ?

以下我們先以區間最大值為例

線段樹長這樣 :

怎們切資料呢 ?

以下我們先以區間最大值為例

線段樹長這樣 :

其中每一個節點對應到原陣列的一個區間

依據我們想要的功能，可以以不同方式定義節點

以區間最大這個功能為例 :

依據我們想要的功能，可以以不同方式定義節點

以區間最大這個功能為例 :

每個點要存的就是對應區間的最大值

依據我們想要的功能，可以以不同方式定義節點

以區間最大這個功能為例 :

每個點要存的就是對應區間的最大值

假設我們已經維護好每個點的數值了

那我們要如何利用些資訊來獲得任意區間的答案呢 ?

那我們要如何利用些資訊來獲得任意區間的答案呢 ?

就是通過合併 !

如果我要求 0~4 項的最大值...

如果我要求 0~4 項的最大值...

如果我要求 1~6 項的最大值...

如果我要求 1~6 項的最大值...

可以證明查詢任何區間，需要用到的點數量是

O(\log_2n)

可以證明查詢任何區間，需要用到的點數量是

O(\log_2n)

因此每次查詢的時間複雜度就是

O(\log_2n)

接下來定義

tree_i 是線段樹上i號點的數值
arr_i 是要處理的原陣列

接下來是如何初始化每個點的數值

接下來是如何初始化每個點的數值

如果對於一個節點 x ，左右子節點分別為 ls、rs

那麼 

tree_x = \max(tree_{ls},tree_{rs})
tree_x = arr_i

如果 x 沒有子節點呢 ?

因此我們可以遞迴地從結節點往上更新

因此我們可以遞迴地從結節點往上更新

時間複雜度就是節點數量為

O(n)

如果我想要更新陣列中其中一個點的數值呢 ?

如果我想要更新陣列中其中一個點的數值呢 ?

以第 4 項為例

那麼只需要更新所區間包含到 4 的節點就好

如果我想要更新陣列中其中一個點的數值呢 ?

以第 4 項為例

那麼只需要更新所區間包含到 4 的節點就好

如果我想要更新陣列中其中一個點的數值呢 ?

以第 4 項為例

只需要更改                    個節點即可

O(\log_2n)

綜合上面所說的，我們可以 :

初始化線段樹 : O(n)
區間查詢 : O(\log_2n)
單點修改 : O(\log_2n)

接下來是實作 

  • 我們通常會將和併兩個子節點稱為 pull
  • 將點 x 的左子節點定義為 x*2 、 右子節點為 x*2 + 1

一些實作細節

segment tree build code

inline void pull(int &x,int ls,int rs){
    x = max(ls,rs);
}
void build(int l,int r,int x){
    if(l==r){
        tree[x] = arr[l];
        return;
    }
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    build(l,mid,ls);
    build(mid+1,r,rs);
    pull(tree[x],tree[ls],tree[rs]);
}

segment tree query code

int query(int a,int b,int l,int r,int x){
    if(l>=a && r<=b) return tree[x];
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    int res = -inf;
    if(mid >= a) res = max(res,query(a,b,l,mid,ls));
    if(mid < b) res = max(res,query(a,b,mid+1,r,rs));
    return res;
}

segment tree modify code

inline void pull(int &x,int ls,int rs){
    x = max(ls,rs);
}
void modify(int a,int l,int r,int x,int v){
    if(l==r){
        tree[x] = v;
        return;
    }
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    if(mid >= a) modify(a,l,mid,ls,v);
    else modify(a,mid+1,r,rs,v);
    pull(tree[x],tree[ls],tree[rs]);
}

max segment tree  code

inline void pull(int &x,int ls,int rs){
    x = max(ls,rs);
}
void build(int l,int r,int x){
    if(l==r){
        tree[x] = arr[l];
        return;
    }
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    build(l,mid,ls);
    build(mid+1,r,rs);
    pull(tree[x],tree[ls],tree[rs]);
}
void modify(int a,int l,int r,int x,int v){
    if(l==r){
        tree[x] = v;
        return;
    }
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    if(mid >= a) modify(a,l,mid,ls,v);
    else modify(a,mid+1,r,rs,v);
    pull(tree[x],tree[ls],tree[rs]);
}
int query(int a,int b,int l,int r,int x){
    if(l>=a && r<=b) return tree[x];
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    int res = -inf;
    if(mid >= a) res = max(res,query(a,b,l,mid,ls));
    if(mid < b) res = max(res,query(a,b,mid+1,r,rs));
    return res;
}

寫寫模板題吧!

Dynamic Range Minimum Queries

{懶標線段樹}

原本的線段樹只能單點修改區間查詢

原本的線段樹只能單點修改區間查詢

但只要加上懶人標記，就可以升級成

區間修改區間查詢 !

原本的線段樹只能單點修改區間查詢

但只要加上懶人標記，就可以升級成

區間修改區間查詢 !

本章使用區間加值，區間求和為例

懶人標記就是我們先不實際更改東西

但記錄一個標記

一旦之後真的需要再依據標記更新線段樹

懶標可以依照自己喜歡的方式定義

以下是我習慣的定義方式 :

如果一個點有懶標 x 

則代表，此節點已經修改

但節點以下的全部節點都還要加值 x

實際是如何運作呢 ?

首先我們定義線段樹上的節點

儲存對應區間的加和

實際是如何運作呢 ?

假設我們要將 3 ~ 7 加值

實際是如何運作呢 ?

假設我們要將 3 ~ 7 加值 x

則我們將兩橘色節點加值 (加上對應區間長度乘以 x)

並各自打上懶標 x

但懶標總不可能一直停在同一個位置吧，什麼時候要移動呢 ?

但懶標總不可能一直停在同一個位置吧，什麼時候要移動呢 ?

答案是當 query、modify 到達有懶標的區間時，

就應該先將懶標傳遞給其子節點

但懶標總不可能一直停在同一個位置吧，什麼時候要移動呢 ?

答案是當 query、modify 到達有懶標的區間時，

就應該先將懶標傳遞給其子節點

要注意的是在傳遞懶標同時要修改節點數值

這個將懶標向下傳遞的動作我們稱為 push

但如果我們將懶標下傳時那個位置原本就有懶標呢 ?

這個將懶標向下傳遞的動作我們稱為 push

但如果我們將懶標下傳時那個位置原本就有懶標呢 ?

這時我們就要將兩個懶標合併 !

例如這個區間加值的懶標就是

直接將舊懶標加上新懶標即可

lazy tag segment tree push、pull code

inline void pull(int &x,int ls,int rs){
    x = ls+rs;
}
void mark(int l,int r,int x,int v){
    tree[x] += (r-l+1)*v;
    tag[x] += v;
}
void push(int l,int r,int x){
    if(tag[x]){
        int ls = x*2, rs = ls+1, mid = (l+r)/2;
        mark(l,mid,ls,tag[x]);
        mark(mid+1,r,rs,tag[x]);
        tag[x] = 0;
    }
}

lazy tag segment tree build code

void build(int l,int r,int x){
    if(l==r){
        tree[x] = arr[l];
        return;
    }
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    build(l,mid,ls);
    build(mid+1,r,rs);
    pull(tree[x],tree[ls],tree[rs]);
}

lazy tag segment tree query code

int query(int a,int b,int l,int r,int x){
    if(l>=a && r<=b) return tree[x];
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    push(l,r,x);
    int res = 0;
    if(mid >= a) res += query(a,b,l,mid,ls);
    if(mid < b) res += query(a,b,mid+1,r,rs);
    return res;
}

lazy tag segment tree modify code

void modify(int a,int b,int l,int r,int x,int v){
    if(l>=a && r<=b){
        mark(l,r,x,v);
        return;
    }
    push(l,r,x);
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    if(mid >= a) modify(a,b,l,mid,ls,v);
    if(mid < b) modify(a,b,mid+1,r,rs,v);
    pull(tree[x],tree[ls],tree[rs]);
}

lazy tag segment tree code

inline void pull(int &x,int ls,int rs){
    x = ls+rs;
}
void build(int l,int r,int x){
    if(l==r){
        tree[x] = arr[l];
        return;
    }
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    build(l,mid,ls);
    build(mid+1,r,rs);
    pull(tree[x],tree[ls],tree[rs]);
}
void mark(int l,int r,int x,int v){
    tree[x] += (r-l+1)*v;
    tag[x] += v;
}
void push(int l,int r,int x){
    if(tag[x]){
        int ls = x*2, rs = ls+1, mid = (l+r)/2;
        mark(l,mid,ls,tag[x]);
        mark(mid+1,r,rs,tag[x]);
        tag[x] = 0;
    }
}
void modify(int a,int b,int l,int r,int x,int v){
    if(l>=a && r<=b){
        mark(l,r,x,v);
        return;
    }
    push(l,r,x);
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    if(mid >= a) modify(a,b,l,mid,ls,v);
    if(mid < b) modify(a,b,mid+1,r,rs,v);
    pull(tree[x],tree[ls],tree[rs]);
}
int query(int a,int b,int l,int r,int x){
    if(l>=a && r<=b) return tree[x];
    int ls = x*2, rs = ls+1, mid = (l+r)/2;
    push(l,r,x);
    int res = 0;
    if(mid >= a) res += query(a,b,l,mid,ls);
    if(mid < b) res += query(a,b,mid+1,r,rs);
    return res;
}

練習題 (包含基本線段樹):

Range Xor Queries

Range Updates and Sums

Dynamic Range Sum Queries

Range Updates and Sums AC code

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 1000006
 
struct node{
    int tag1=0,tag2=0,sum=0;
};
int n,q;
node tree[maxn*4];
void mark1(int l,int r,int x,int v){  // 加值
    tree[x].tag1 += v;
    tree[x].sum += v*(r-l+1);
}
void mark2(int l,int r,int x,int v){  // 改值
    tree[x].tag2 = v;
    tree[x].sum = v*(r-l+1);
    tree[x].tag1 = 0;
}
void pushdown(int l,int r,int x){
    int ls = x*2, rs = ls+1, m =(l+r)/2;
    if(tree[x].tag2){
        mark2(l,m,ls,tree[x].tag2);
        mark2(m+1,r,rs,tree[x].tag2);
        tree[x].tag2 = 0;
    }
    if(tree[x].tag1){
        mark1(l,m,ls,tree[x].tag1);
        mark1(m+1,r,rs,tree[x].tag1);
        tree[x].tag1 = 0;
    }
}
void modify(int a,int b,int l,int r,int x,int v,int op){
    if(l>=a && r<=b){
        if(!op) mark1(l,r,x,v);
        else mark2(l,r,x,v);
        return;
    }
    int ls = x*2, rs = ls+1, m = (l+r)/2;
    pushdown(l,r,x);
    if(m >= a) modify(a,b,l,m,ls,v,op);
    if(m < b) modify(a,b,m+1,r,rs,v,op);
    tree[x].sum = tree[ls].sum + tree[rs].sum;
}
int query(int a,int b,int l,int r,int x){
    if(l>=a && r<=b) return tree[x].sum;
    int ls = x*2, rs = ls+1,m = (l+r)/2;
    pushdown(l,r,x);
    int res = 0;
    if(m >= a) res += query(a,b,l,m,ls);
    if(m < b) res += query(a,b,m+1,r,rs);
    return res;
}
set<int> st;
 
int ask(int y){
    if(st.count(y)){
        auto it = st.lower_bound(y);
        int L = (it == st.begin())?1:((*(--it))+1);
        if(L <= y-1){
            int tmp = query(L,y-1,1,n,1);
            modify(L,y-1,1,n,1,0,1);
            modify(y,y,1,n,1,tmp,0);
        }
        return query(y,y,1,n,1);
    }else{
        return 0;
    }
}
 
main(){
    cin>>n>>q;
    for(int i=1;i<=n;++i){
        int a; cin>>a;
        modify(i,i,1,n,1,a,0);
    }
    while(q--){
        int op; cin>>op;
        if(op==1){
            int l,r,x; cin>>l>>r>>x;
            modify(l,r,1,n,1,x,0);
        }else if(op==2){
            int l,r,x; cin>>l>>r>>x;
            modify(l,r,1,n,1,x,1);
        }else{
            int l,r; cin>>l>>r;
            cout<<query(l,r,1,n,1)<<endl;
        }
    }
}

Code

By maxbrucelen

Made with Slides.com

Code

  • 138

More from maxbrucelen