{進階樹論}

by maxbrucelen

{樹鍊剖分}

Heavy-Light Decomposition

樹鍊剖分是一個將樹切分的方法

我們可以依照切分的區塊套上資料結構

達成一些在樹路徑上的操作

我們從一個例題開始 :

這題的重點就是

如何在樹上的一條路徑求最大點權

這題的重點就是

如何在樹上的一條路徑求最大點權

我們已經會了幾個可以求區間極值的資結了

有線段樹、ST表等

我們已經會了幾個可以求區間極值的資結了

有線段樹、ST表等

樹鍊剖分要做的就是將樹切分，方便我們套上資結

我們已經會了幾個可以求區間極值的資結了

有線段樹、ST表等

樹鍊剖分要做的就是將樹切分，方便我們套上資結

EX :

切分完後，我們將每個區塊對應到一個陣列的連續區間

切分完後，我們將每個區塊對應到一個陣列的連續區間

切分完後，我們將每個區塊對應到一個陣列的連續區間

切分完後，我們將每個區塊對應到一個陣列的連續區間

切分完後，我們將每個區塊對應到一個陣列的連續區間

切分完後，我們將每個區塊對應到一個陣列的連續區間

切分完後，我們將每個區塊對應到一個陣列的連續區間

接著我們對這個陣列開一個資料結構

例如線段樹

接著，每當我要查詢一條路徑的資訊，我只需要對這棵線段樹的某些區間查詢，再把結果合併即可

假設我要查詢 A、B 兩點路徑的最小值...

假設我要查詢 A、B 兩點路徑的最小值...

我只需要查詢這幾個區間(綠色框框)即可

因此目前的時間複雜度為

O(要查詢的區間數量 \cdot 資結每次查詢的時間複雜度)

因此目前的時間複雜度為

O(要查詢的區間數量 \cdot 資結每次查詢的時間複雜度)

如果是線段樹 :

O(要查詢的區間數量 \cdot \log_2(n))

所以我們現在就需要一個好的分割方法

能保證要詢問的區間數量不多 !

O(要查詢的區間數量 \cdot \log_2(n))

所以我們現在就需要一個好的分割方法

能保證要詢問的區間數量不多 !

O(要查詢的區間數量 \cdot \log_2(n))

這就是樹鍊剖分要做的事情 !

在介紹如何分割之前，先定義一些名詞 :

  • 重兒子 : 一個點的子節點中，子樹大小最大的那個子節點
  • 輕兒子 : 除了重兒子以外的所有子節點
  • 重邊 : 點連接其重兒子的邊
  • 輕邊 : 點連接其輕兒子的邊

對於一棵樹，我們先算出每一個節點的重兒子

對於一棵樹，我們先算出每一個節點的重兒子

接著連上每一條重邊，

只看重邊的每一個連通塊就是重鍊

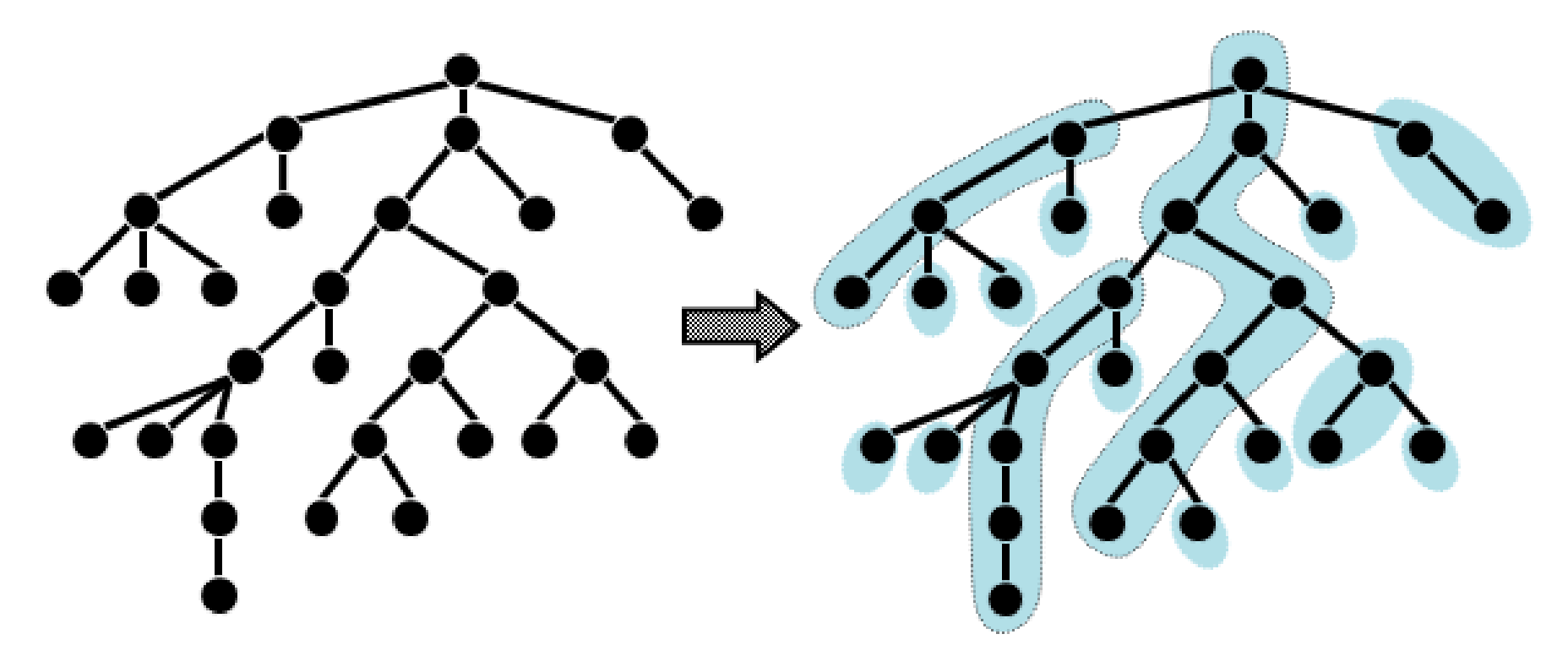
這樣就分割好了 !

接下來就只要將每條重鍊對應到

線段樹中的一個區間即可

接下來要來看看這樣切分

最多只有多少個區間需要查詢

對於每一個查詢，兩點有一個LCA

對於每一個查詢，兩點有一個LCA

我們可以將查詢看成做兩次查詢

分別是 A~LCA、B~LCA

可以發現，這樣一個查詢所需要查詢的區間數量

就是從 A 走到 LCA 的換鍊次樹 !

(從一條重鍊換到另一條的次數)

那需要換幾次鍊呢 ?

每換一次鍊，就代表動點此時在輕小孩

也就代表動點所包含的子樹大小變成原本的

兩倍以上 !

假設有一個動點在 A，一直走到 LCA

那需要換幾次鍊呢 ?

每換一次鍊，就代表動點此時在輕小孩

也就代表動點所包含的子樹大小變成原本的

兩倍以上 !

假設有一個動點在 A，一直走到 LCA

一棵樹也就 n 個點，有幾次可以給它換鍊呢 ?

就是 

\log_2n

總結上面所說的 :

每次查詢需要對資結查詢的次數就是

從其中一點走到 LCA 的換鍊次數(數量級相同) 為

\log_2n

總結上面所說的 :

每次查詢需要對資結查詢的次數就是

從其中一點走到 LCA 的換鍊次數(數量級相同) 為

\log_2n
O(要查詢的區間數量 \cdot 資結每次查詢的時間複雜度)

因此時間複雜度為

總結上面所說的 :

每次查詢需要對資結查詢的次數就是

從其中一點走到 LCA 的換鍊次數(數量級相同) 為

\log_2n
O(要查詢的區間數量 \cdot 資結每次查詢的時間複雜度)

因此時間複雜度為

= O(\log_2n \cdot 資結每次查詢的時間複雜度)
= O((\log_2n)^2 )

(如果是線段樹)

因此我們就會解這題了 !

複雜度為

O(n \log_2 n+q \cdot \log_2n \cdot \log_2n )

如何實作 ?

通常會分成兩步 :

  1. DFS 記錄子樹大小、重小孩、結點深度、結點的父結點

首先是 build 

通常會分成兩步 :

  1. DFS 記錄子樹大小、重小孩、結點深度、結點的父結點
  2. 依照重小孩，連接重邊形成重鍊、紀錄此點所在的鍊編號               (鍊頂的結點編號)，並以 DFS 序將結點對應到資料結構

首先是 build 

1. 假設詢問 AB 兩點，維持 A 所在的鍊頂深度 > B 所在的鍊頂深度

接著是查詢 : 

(不符合就 swap 兩點)

1. 假設詢問 AB 兩點，維持 A 所在的鍊頂深度 > B 所在的鍊頂深度

接著是查詢 : 

(不符合就 swap 兩點)

2. 每次對線段樹查詢 A 點到其鍊頂的區間

1. 假設詢問 AB 兩點，維持 A 所在的鍊頂深度 > B 所在的鍊頂深度

接著是查詢 : 

(不符合就 swap 兩點)

2. 每次對線段樹查詢 A 點到其鍊頂的區間

3. 將A點跳至鍊頂的父結點 (換鍊)

1. 假設詢問 AB 兩點，維持 A 所在的鍊頂深度 > B 所在的鍊頂深度

接著是查詢 : 

(不符合就 swap 兩點)

2. 每次對線段樹查詢 A 點到其鍊頂的區間

3. 將A點跳至鍊頂的父結點 (換鍊)

4. 重複至AB兩點位於同一條重鍊

1. 假設詢問 AB 兩點，維持 A 所在的鍊頂深度 > B 所在的鍊頂深度

接著是查詢 : 

(不符合就 swap 兩點)

2. 每次對線段樹查詢 A 點到其鍊頂的區間

3. 將A點跳至鍊頂的父結點 (換鍊)

4. 重複至AB兩點位於同一條重鍊

5. 最終查詢 AB 所對應的區間

 CODE 以這題為例

變數 :

int n,hs[],f[],sz[],d[],val[],tp[],dfn[],timer,arr[],tree[];

分別為:

結點數、重小孩、父結點、子數大小、

結點深度、點權、鍊頂、DFS序、DFS序計數器、

線段數對應的陣列、線段樹

Section 1 : DFS

inline void dfs(int x,int p){
    sz[x] = 1;
    hs[x] = -1;
    for(int i:E[x]){
        if(i==p) continue;
        f[i] = x;
        d[i] = d[x]+1;
        dfs(i,x);
        sz[x] += sz[i];
        if(hs[x]==-1||sz[hs[x]] < sz[i]) hs[x] = i;
    }
}

Section 2 : LINK

inline void link(int x,int top){
    tp[x] = top;
    dfn[x] = ++timer;
    arr[timer] = val[x];
    if(hs[x]!=-1) link(hs[x],top);
    for(int i:E[x]){
        if(i==f[x] || i==hs[x]) continue;
        link(i,i);
    }
}

Section 3 : query-jump

inline int jump(int a,int b){
    int mx = 0;
    while(tp[a]!=tp[b]){
        if(d[tp[b]]>d[tp[a]]) swap(a,b);
        mx = max(mx,query(dfn[tp[a]],dfn[a],1,n,1));
        a = f[tp[a]];
    }
    if(dfn[a]>dfn[b]) swap(a,b);
    mx = max(mx,query(dfn[a],dfn[b],1,n,1));
    return mx;
}

完整AC code

#include<bits/stdc++.h>
using namespace std;
#define maxn 200005
vector<int> E[maxn];
int n,hs[maxn],f[maxn],sz[maxn],d[maxn],val[maxn],tp[maxn],dfn[maxn],timer,arr[maxn],tree[maxn*4],q;
inline void dfs(int x,int p){
    sz[x] = 1;
    hs[x] = -1;
    for(int i:E[x]){
        if(i==p) continue;
        f[i] = x;
        d[i] = d[x]+1;
        dfs(i,x);
        sz[x] += sz[i];
        if(hs[x]==-1||sz[hs[x]] < sz[i]) hs[x] = i;
    }
}
inline void link(int x,int top){
    tp[x] = top;
    dfn[x] = ++timer;
    arr[timer] = val[x];
    if(hs[x]!=-1) link(hs[x],top);
    for(int i:E[x]){
        if(i==f[x] || i==hs[x]) continue;
        link(i,i);
    }
}
inline void build(int l,int r,int x){
    if(l==r){tree[x] = arr[l]; return;}
    int ls = x*2, rs = ls+1, m = (l+r)/2;
    build(l,m,ls);
    build(m+1,r,rs);
    tree[x] = max(tree[ls],tree[rs]);
}
inline void modify(int a,int l,int r,int x,int v){
    if(l==r){tree[x] = v;return;}
    int ls = x*2, rs = ls+1, m = (l+r)/2;
    if(m>=a) modify(a,l,m,ls,v);
    else  modify(a,m+1,r,rs,v);
    tree[x] = max(tree[ls],tree[rs]);
}
inline int query(int a,int b,int l,int r,int x){
    if(l>=a&&r<=b) return tree[x];
    int ls = x*2, rs = ls+1, m = (l+r)/2;
    int mx = 0;
    if(m>=a) mx = max(mx,query(a,b,l,m,ls));
    if(m<b) mx = max(mx,query(a,b,m+1,r,rs));
    return mx;
}
inline int jump(int a,int b){
    int mx = 0;
    while(tp[a]!=tp[b]){
        if(d[tp[b]]>d[tp[a]]) swap(a,b);
        mx = max(mx,query(dfn[tp[a]],dfn[a],1,n,1));
        a = f[tp[a]];
    }
    if(dfn[a]>dfn[b]) swap(a,b);
    mx = max(mx,query(dfn[a],dfn[b],1,n,1));
    return mx;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin>>n>>q;
    for(int i=1;i<=n;++i) cin>>val[i];
    for(int i=1;i<n;++i){
        int a,b; cin>>a>>b;
        E[a].push_back(b);
        E[b].push_back(a);
    }
    dfs(1,0);
    link(1,1);
    build(1,n,1);
    while(q--){
        int a,b,c; cin>>a>>b>>c;
        if(a==1) modify(dfn[b],1,n,1,c);
        else cout<<jump(b,c)<<' ';
    }
    return 0;
}

練習題 :

ABC 294G

染色

樹重心分治、樹重心剖分

Centroid Decomposition

首先定義樹重心 :

 

一個點v為樹重心(centroid)則移除v後
最大連通塊大小不超過 \left\lfloor N/2\right\rfloor

樹重心這個性質很像我們在分治的時候

每次將序列切成平均的兩半

因此我們可以利用這個性質在樹上分治

樹重心這個性質很像我們在分治的時候

每次將序列切成平均的兩半

因此我們可以利用這個性質在樹上分治

Fixed-Length Paths I

我們可以考慮對每一個點

枚舉所有經過他、且長度為 k 的路徑

 

但是直接這樣做的複雜度為

O(n^2)

我們會發現剛剛的方法做了非常多重複的事情

(同一條路會被多次算到)

我們可以每次求出樹重心 C

以 C 為中點枚舉所有經過 C 

且長度為 k 的路徑

我們可以每次求出樹重心 C

以 C 為中點枚舉所有經過 C 

且長度為 k 的路徑

接下來將 C 從圖中拔走

繼續對每個連通塊遞迴處理

會發現因為 C 已經被拔走

所以之後不會再次算到相同路徑

並且每次拔走重心，可以將每個子樹大小

至少縮減為原本的 1/2
因此遞迴深度不超過               

\log_2n

每次計算一個子圖 (遞迴到一半)

的時間複雜度為 T(n) (n為子圖點數量)

每次計算一個子圖 (遞迴到一半)

的時間複雜度為 T(n) (n為子圖點數量)

如果總點數為 N ，總時間複雜度就是

O(N \log_2 N)

Fixed-Length Paths I    ACcode

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define maxn 200005
#define endl '\n'
 
int n,mxd,as,K,sz[maxn],cnt[maxn];
vector<int> E[maxn];
bitset<maxn> vi;
 
void dfs_sz(int x,int p){
    sz[x] = 1;
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        dfs_sz(i,x);
        sz[x] += sz[i];
    }
}
int find_c(int x,int p,int tot){
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        if(sz[i]*2 > tot) return find_c(i,x,tot);
    }
    return x;
}
void update(int x,int p,int d){
    if(d > K) return;
    cnt[d]++;
    mxd = max(mxd,d);
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        update(i,x,d+1);
    }
}
void dfs_cal(int x,int p,int d){
    if(d > K) return;
    if(K-d<=mxd) as += cnt[K-d];
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        dfs_cal(i,x,d+1);
    }
}
 
void dfs_cd(int x){
    dfs_sz(x,0);
    int c = find_c(x,0,sz[x]);
    vi[c] = 1;
    mxd = 0;
    for(int i:E[c]){
        if(vi[i]) continue;
        dfs_cal(i,0,1);
        update(i,0,1);
    }
    if(K<=mxd) as += cnt[K];
    for(int i=0;i<=mxd+1;++i) cnt[i] = 0;
    for(int i:E[c]){
        if(vi[i]) continue;
        dfs_cd(i);
    }
}
 
main(){
    ios::sync_with_stdio(0); cin.tie(0);
    cin>>n>>K;
    for(int i=1;i<n;++i){
        int a,b; cin>>a>>b;
        E[a].push_back(b);
        E[b].push_back(a);
    }
    dfs_cd(1);
    cout<<as<<endl;
}

接下來要介紹一個東西叫重心樹

我們直接定義如何構造它

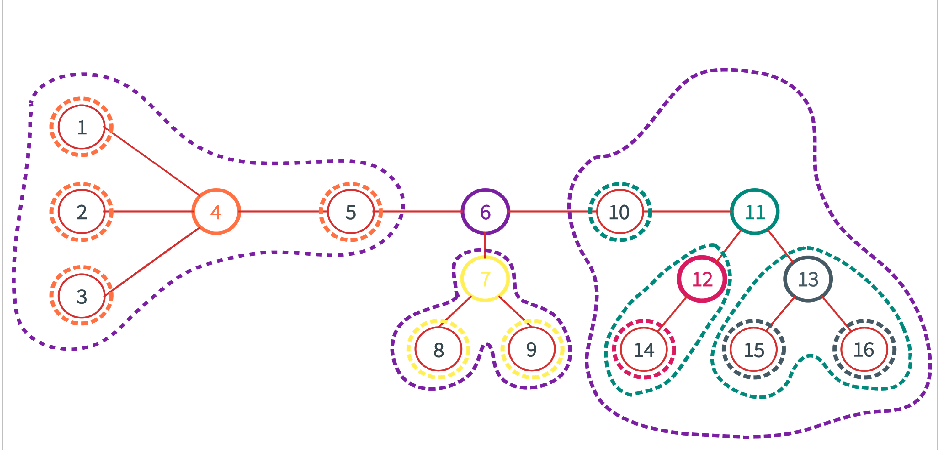
  • 先找出樹中的樹重心 C
  • 將 C 移除並遞迴處理每個連通塊
  • 將 C 設為所有聯通塊重心的父結點

構造重心樹 code

void dfs_sz(int x,int p){
    sz[x] = 1;
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        dfs_sz(i,x);
        sz[x] += sz[i];
    }
}
int find_c(int x,int p,int tot){
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        if(sz[i]*2 > tot) return find_c(i,x,tot);
    }
    return x;
}
void build_cd(int x,int p){
    dfs_sz(x,0);
    int c = find_c(x,0,sz[x]);
    vi[c] = 1;
    pa[c] = p;
    for(int i:E[c]){
        if(i==p || vi[i]) continue;
        build_cd(i,c);
    }
}

構造出這棵樹之後，它有一些性質讓我們使用

構造出這棵樹之後，它有一些性質讓我們使用

  1. 它的深度不超過 logn
  2. 原樹上任兩個的路徑一定經過他們在重心樹上的LCA

 

E. Xenia and Tree

想想看重心樹的兩種性質...

想想看重心樹的兩種性質...

就可以發現如果我要詢問離點 A 最近的紅色(假設為點B)

因為原樹上任兩個的路徑一定經過他們在重心樹上的LCA

 

想想看重心樹的兩種性質...

就可以發現如果我要詢問離點 A 最近的紅色(假設為點B)

因為原樹上任兩個的路徑一定經過他們在重心樹上的LCA

 

所以所有 A 在重心樹上的祖先，一定有至少一個在原樹上在 A~B的路徑上 !

因此我只要維護好每個點的子樹中

與它最近的紅點距離即可

因此我只要維護好每個點的子樹中

與它最近的紅點距離即可

這樣就可以在查詢時查詢每個祖先即可

因此我只要維護好每個點的子樹中

與它最近的紅點距離即可

這樣就可以在查詢時查詢每個祖先即可

唯一要注意的是兩點距離是原樹上的距離!!!!!

(LCA求)

E. Xenia and Tree AC code

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define endl '\n'
#define maxn 200005

int n,m,d[maxn],sz[maxn],anc[maxn][25],pa[maxn],vi[maxn],mn[maxn];
vector<int> E[maxn];

void init(){
    for(int i=1;i<=n;++i) mn[i] = inf;
}

void dfs(int x,int p){
    for(int i:E[x]){
        if(i==p) continue;
        d[i] = d[x]+1;
        anc[i][0] = x;
        dfs(i,x);
    }
}
inline int lca(int a,int b){
    if(d[b] > d[a]) swap(a,b);
    int dh = d[a]-d[b];
    for(int i=0;i<=24;++i) if(dh&(1<<i)) a = anc[a][i];
    if(a==b) return a;
    for(int i=24;i>=0;--i){
        if(anc[a][i] != anc[b][i]){
            a = anc[a][i];
            b = anc[b][i];
        }
    }
    return anc[a][0];
}
inline int cal(int a,int b){
    return d[a]+d[b]-2*d[lca(a,b)];
}

void dfs_sz(int x,int p){
    sz[x] = 1;
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        dfs_sz(i,x);
        sz[x] += sz[i];
    }
}
int find_c(int x,int p,int tot){
    for(int i:E[x]){
        if(i==p || vi[i]) continue;
        if(sz[i]*2 > tot) return find_c(i,x,tot);
    }
    return x;
}
void build_cd(int x,int p){
    dfs_sz(x,0);
    int c = find_c(x,0,sz[x]);
    vi[c] = 1;
    pa[c] = p;
    for(int i:E[c]){
        if(i==p || vi[i]) continue;
        build_cd(i,c);
    }
}

void add(int x){
    int pos = x;
    while(pos != 0){
        mn[pos] = min(mn[pos],cal(x,pos));
        pos = pa[pos];
    }
}
int query(int x){
    int res = inf,pos = x;
    while(pos!=0){
        res = min(res,mn[pos]+cal(x,pos));
        pos = pa[pos];
    }
    return res;
}

main(){
    ios::sync_with_stdio(0); cin.tie(0);
    cin>>n>>m;
    init();
    for(int i=1;i<n;++i){
        int a,b; cin>>a>>b;
        E[a].push_back(b);
        E[b].push_back(a);
    }
    dfs(1,0);
    for(int i=1;i<=24;++i) for(int j=1;j<=n;++j)
        anc[j][i] = anc[anc[j][i-1]][i-1];
    build_cd(1,0);
    add(1);

    while(m--){
        int op,x; cin>>op>>x;
        if(op==1){
            add(x);
        }else{
            cout<<query(x)<<endl;
        }
    }
}

練習題 :

我要成為海賊王

這題我被 TLE 至少30次，所以我想放code哈

#include<bits/stdc++.h>
#pragma GCC optimize("Ofast,unroll-loops,no-stack-protector,fast-math")
#pragma GCC target("lzcnt,popcnt,tune=native")
using namespace std;
using LL = long long;
#define inf 1e18
#define maxn 100005
#define endl '\n'
LL AS[maxn],arr[maxn],dis[maxn];
int n,sz[maxn],pa[maxn],q,num[maxn],to[maxn];
vector<pair<int,int>> E[maxn];
vector<pair<int,LL>> up[maxn];
vector<LL> sub[maxn];
bitset<maxn> vi,bt;
bool f1,f2;

void dfs_sz(int x,int p){
    sz[x] = 1;
    for(const auto&i:E[x]){
        if(i.first==p || vi[i.first]) continue;
        dfs_sz(i.first,x);
        sz[x] += sz[i.first];
    }
}
int find_c(int x,int p,const int &tot){
    for(const auto &i:E[x]){
        if(i.first==p || vi[i.first]) continue;
        if(sz[i.first]*2 > tot) return find_c(i.first,x,tot);
    }
    return x;
}
void dfs(const int &root,int x,int p){
    up[x].emplace_back(root,dis[x]);
    for(const auto &i:E[x]){
        if(i.first == p || vi[i.first]) continue;
        dis[i.first] = dis[x]+i.second;
        dfs(root,i.first,x);
    }
}
inline void build_cd(int x,int p){
    dfs_sz(x,0);
    int c = find_c(x,0,sz[x]);
    pa[c] = p;
    vi[c] = 1;
    to[c] = sub[p].size();
    sub[p].emplace_back(0);
    up[c].emplace_back(c,0);
    for(const auto &i:E[c]){
        if(vi[i.first]) continue;
        dis[i.first] = i.second;
        dfs(c,i.first,0);
        build_cd(i.first,c);
    }
}
main(){
    ios::sync_with_stdio(0); cin.tie(0);
    cin>>n>>q;
    memset(AS,-1,sizeof(AS));
    for(int i=1;i<n;++i){
        int a,b,c; cin>>a>>b>>c;
        a++,b++;
        E[a].emplace_back(b,c);
        E[b].emplace_back(a,c);
    }
    build_cd(1,0);
    for(int i=1;i<=n;++i) reverse(up[i].begin(),up[i].end());
    for(int i=1;i<=q;++i){
        int op,x; cin>>op>>x;
        x++;
        if(op==1){
            f1 = f2;
            if(bt[x]) continue;
            bt[x] = 1;
            int it = 0;
            for(const auto &pos:up[x]){
                arr[pos.first] += pos.second;
                if(pa[pos.first]) sub[pa[pos.first]][to[pos.first]] += up[x][it+1].second;
                num[pos.first]++;
                it++;
            }
        }else{
            f2 = 1;
            if(!f1 && AS[x]!=-1){
                cout<<AS[x]<<endl;
                continue;
            }
            int last = 0;
            LL as = 0;
            for(const auto &pos:up[x]){
                as += arr[pos.first];
                if(last) as -= sub[pos.first][to[last]];
                as += (num[pos.first]-num[last])*pos.second;
                last = pos.first;
            }
            AS[x] = as;
            cout<<as<<endl;
        }
    }
}

{虛樹}

Virtual Tree

虛樹用來處理一些每次詢問只和樹上的一些結點有關的問題

ABC 359G

給定一棵樹

每次詢問給 k 個點，詢問其中每個點對在樹上的距離和

全部詢問 k 總和不超過 n

如果 k = n 呢?

如果 k = n 呢?

直接換根 dp 就好了 !

但現在每次詢問都是不同的點集合

如果 k = n 呢?

直接換根 dp 就好了 !

但現在每次詢問都是不同的點集合

這時候就是虛樹派上用場的時候了 !

我們可以花費 O(klogn) 的時間

蓋出一棵虛樹

上面包含了至多 2k 個點 

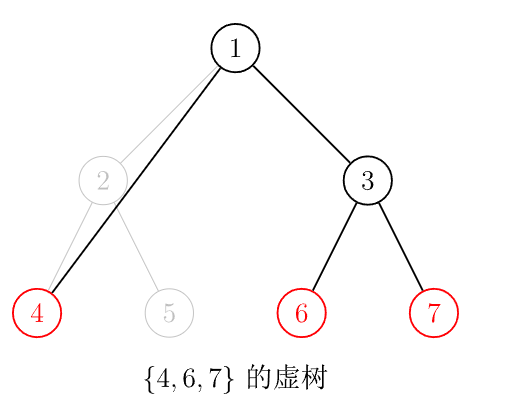
我們可以花費 O(klogn) 的時間

蓋出一棵虛樹

上面包含了至多 2k 個點 

並且虛樹上面的祖孫關係會保持不變

因此求距離也不會壞

簡單講構造虛樹就是

在原來的 K 的點外

選擇一些輔助點、並連接一些虛邊

達到祖孫關係不變的效果

簡單講構造虛樹就是

在原來的 K 的點外

選擇一些輔助點、並連接一些虛邊

達到祖孫關係不變的效果

你用直覺也一定構的出來

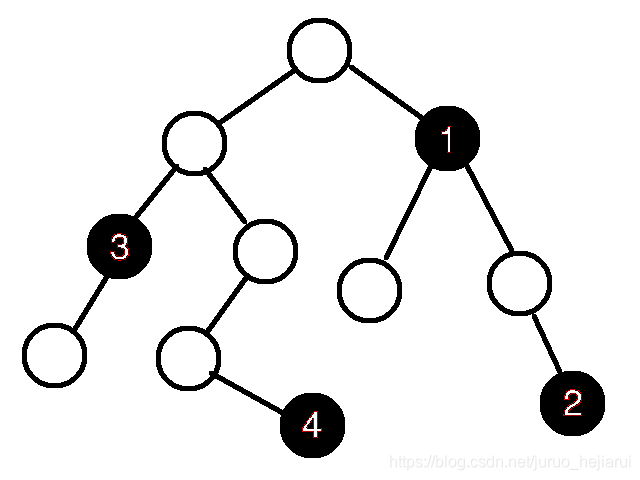
簡單講構造虛樹就是

在原來的 K 的點外

選擇一些輔助點、並連接一些虛邊

達到祖孫關係不變的效果

你用直覺也一定構的出來

有很多種構造方法，這邊介紹一種簡潔的

(我只會這個)

假設有一個陣列 A 裡面有這次詢問的 k 個點

首先我們先將他們依照 DFS 序排序

假設有一個陣列 A 裡面有這次詢問的 k 個點

首先我們先將他們依照 DFS 序排序

這時候會有性質 : 相鄰兩點的 LCA

一定包含所有點對的 LCA

假設有一個陣列 A 裡面有這次詢問的 k 個點

首先我們先將他們依照 DFS 序排序

這時候會有性質 : 相鄰兩點的 LCA

一定包含所有點對的 LCA

因此我們將所有相鄰點 LCA 也加入 A 後

A 中就已經有所有虛樹中的點

但由於可能有些相鄰點的LCA會重複

所以要對 A 去重 ( A中還是維持以DFS序排序 )

但由於可能有些相鄰點的LCA會重複

所以要對 A 去重 ( A中還是維持以DFS序排序 )

接下來要幫虛樹建邊，我們用以下構造方法 :

但由於可能有些相鄰點的LCA會重複

所以要對 A 去重 ( A中還是維持以DFS序排序 )

接下來要幫虛樹建邊，我們用以下構造方法 :

枚舉每序列中每對相鄰的兩點 A、B

並建邊連接  LCA(A,B) 、 B 兩點

(若有需要邊權也可以加)

來看看建構虛樹

不精美的動畫吧

紅色點是詢問需要的點

紅色點是詢問需要的點

橘色是為了建構虛樹多加的點

枚舉每序列中每對相鄰的兩點 A、B

並建邊連接  LCA(A,B) 、 B 兩點

枚舉每序列中每對相鄰的兩點 A、B

並建邊連接  LCA(A,B) 、 B 兩點

枚舉每序列中每對相鄰的兩點 A、B

並建邊連接  LCA(A,B) 、 B 兩點

枚舉每序列中每對相鄰的兩點 A、B

並建邊連接  LCA(A,B) 、 B 兩點

枚舉每序列中每對相鄰的兩點 A、B

並建邊連接  LCA(A,B) 、 B 兩點

枚舉每序列中每對相鄰的兩點 A、B

並建邊連接  LCA(A,B) 、 B 兩點

可以發現與原本祖孫關係不變

這樣子建構的總時間複雜度為

排序、 去重: O(k \log_2 k)
建邊 : O(k \log_2 n)

這樣子建構的總時間複雜度為

排序、 去重: O(k \log_2 k)
建邊 : O(k \log_2 n)
O(k \log_2 k + k \log_2n) = O(k \log_2n)

build virtual tree code section 1 : DFS+build LCA

bool comp(int a,int b){
    return dfn[b] > dfn[a];
}
void dfs(int x,int p){
    dfn[x] = ++timer;
    for(int i:E[x]){
        if(i==p) continue;
        d[i] = d[x]+1;
        anc[i][0] = x;
        dfs(i,x);
    }
}

int lca(int a,int b){
    if(d[b] > d[a]) swap(a,b);
    int dh = d[a]-d[b];
    for(int i=0;i<=25;++i) if(dh&(1<<i)) a = anc[a][i];
    if(a==b) return a;
    for(int i=25;i>=0;--i){
        if(anc[a][i] != anc[b][i]){
            a = anc[a][i];
            b = anc[b][i];
        }
    }
    return anc[a][0];
}

build virtual tree code section 2 : build virtual tree

inline void init(){
    for(int i:rec) E2[i].clear();
    rec.clear();
}
inline void con(int a,int b){
    E2[a].push_back(b);
    E2[b].push_back(a);
    rec.push_back(a);
    rec.push_back(b);
}
inline void build(vector<int> &h){
    sort(h.begin(),h.end(),comp);
    vector<int> tmp;
    int len = h.size();
    for(int i=0;i<len-1;++i){
        tmp.push_back(h[i]);
        tmp.push_back(lca(h[i],h[i+1]));
    }
    tmp.push_back(h.back());
    sort(tmp.begin(),tmp.end(),comp);
    tmp.resize(unique(tmp.begin(),tmp.end())-tmp.begin());
    for(int i=0;i<(int)tmp.size()-1;++i){
        int lc = lca(tmp[i],tmp[i+1]);
        con(tmp[i+1],lc);
    }
}

ABC 359G

給定一棵樹

每次詢問給 k 個點，詢問其中每個點對在樹上的距離和

回到這題看看怎麼解吧 !

每次詢問我們可以花費                        的時間建構一個只有 2k 個點的虛樹

(帶邊權的)

O(k\log_2n)

每次詢問我們可以花費                        的時間建構一個只有 2k 個點的虛樹

(帶邊權的)

O(k\log_2n)

接下來直接對它換跟 DP 就可以求出

所有點對距離了

AC code

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define endl '\n'
#define maxn 200005

int n,arr[maxn],d[maxn],anc[maxn][30],dfn[maxn],timer,dp[maxn],sz[maxn],as;
vector<int> E[maxn],p[maxn],rec;
vector<pair<int,int>> E2[maxn];
set<int> st;
bool comp(int a,int b){
    return dfn[b] > dfn[a];
}
void dfs(int x,int p){
    dfn[x] = ++timer;
    for(int i:E[x]){
        if(i==p) continue;
        d[i] = d[x]+1;
        anc[i][0] = x;
        dfs(i,x);
    }
}
int lca(int a,int b){
    if(d[b]>d[a]) swap(a,b);
    int dh = d[a]-d[b];
    for(int i=0;i<=25;++i) if(dh&(1<<i)) a = anc[a][i];
    if(a==b) return a;
    for(int i=25;i>=0;--i){
        if(anc[a][i] != anc[b][i]){
            a = anc[a][i];
            b = anc[b][i];
        }
    }
    return anc[a][0];
}
void init(){
    for(int i:rec) E2[i].clear(),dp[i] = 0,sz[i] = 0;
    rec.clear();
    st.clear();
}
void conect(int a,int b,int w){
    E2[a].push_back({b,w});
    E2[b].push_back({a,w});
    rec.push_back(a);
    rec.push_back(b);
}
pair<int,int> build(vector<int> &h){
    sort(h.begin(),h.end(),comp);
    vector<int> tmp;
    int len = h.size();
    for(int i=0;i<len-1;++i){
        tmp.push_back(h[i]);
        tmp.push_back(lca(h[i],h[i+1]));
    }
    tmp.push_back(h.back());
    sort(tmp.begin(),tmp.end(),comp);
    tmp.resize(unique(tmp.begin(),tmp.end())-tmp.begin());
    set<int> num;
    for(int i=0;i<(int)tmp.size()-1;++i){
        int lc = lca(tmp[i],tmp[i+1]);
        int lc2 = lca(lc,tmp[i+1]);
        conect(tmp[i+1],lc,d[lc]+d[tmp[i+1]]-2*d[lc2]);
        num.insert(tmp[i+1]);
        num.insert(lc);
    }
    return {tmp.back(),num.size()};
}
void dfs2(int x,int p){
    if(st.count(x)){
        sz[x] = 1;
        dp[x] = 0;
    }else{
        sz[x] = 0;
        dp[x] = 0;   
    }
    for(auto i:E2[x]){
        if(i.first==p) continue;
        dfs2(i.first,x);
        dp[x] += i.second*sz[i.first]+dp[i.first];
        sz[x] += sz[i.first];
    }
}
void dfs3(int x,int p,int N){
    if(st.count(x)) as += dp[x];
    for(auto i:E2[x]){
        if(i.first==p) continue;
        dp[i.first] = dp[x]-sz[i.first]*i.second+(N-sz[i.first])*i.second;
        dfs3(i.first,x,N);
    }
}

main(){
    ios::sync_with_stdio(0); cin.tie(0);
    cin>>n;
    for(int i=1;i<n;++i){
        int a,b; cin>>a>>b;
        E[a].push_back(b);
        E[b].push_back(a);
    }
    for(int i=1;i<=n;++i) cin>>arr[i];
    for(int i=1;i<=n;++i) p[arr[i]].push_back(i);
    dfs(1,0);
    for(int i=1;i<=25;++i){
        for(int j=1;j<=n;++j){
            anc[j][i] = anc[anc[j][i-1]][i-1];
        }
    }

    for(int i=1;i<=n;++i){ //            modify
        if(p[i].empty()) continue;
        init();
        int tmp  = as;
        for(int j:p[i]) st.insert(j);
        pair<int,int> res = build(p[i]);
        int root = res.first;
        int N = res.second;
        dfs2(root,0);
        dfs3(root,0,p[i].size());
    }
    cout<<as/2<<endl;
}

練習題 :

CF 613 D

P2495

Code

By maxbrucelen

Made with Slides.com

Code

  • 99

More from maxbrucelen