計算幾何

Computational geometry

 

  • 座標、向量、基本向量計算、應用
  • 線段相交、線段交點
  • 點到直線的距離
  • 凸包
  • 極角排序
  • 其他

 

目錄

向量基礎介紹

向量?

由一個pair組成

可以看成是從始點到終點

x、y座標分別動了多少

 

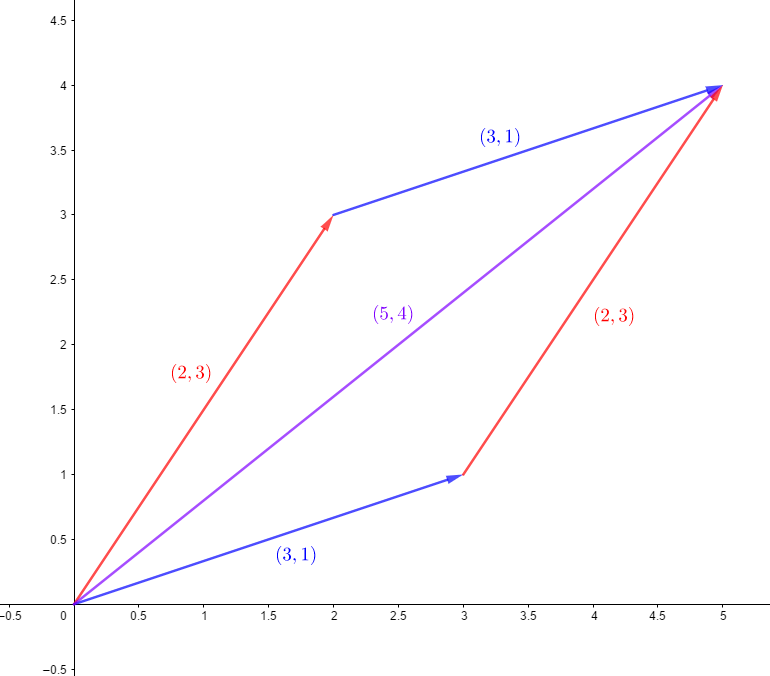
向量加法

直接將兩個分量分別相加

 

 

會指向兩項量組成的平行四邊形另一端

 

 

(a,b) + (c,d) = (a+c,b+d)

向量減法

直接將兩個分量分別相減

 

 

可以看成是加上一條相反的向量

 

 

(a,b) - (c,d) = (a-c,b-d)

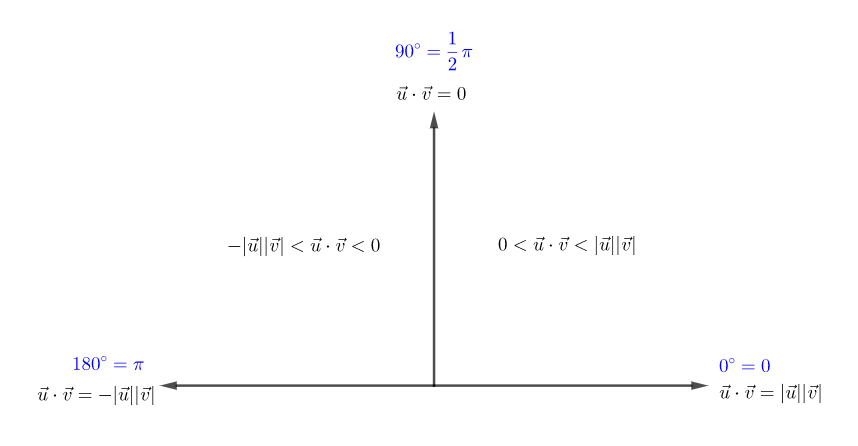
向量內積 (dot)

\vec{u} • \vec{v} = |\vec{u}||\vec{v}|cos(\theta)
\vec{u} = (X_u,Y_u)
\vec{v} = (X_v,Y_v)

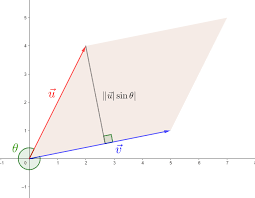
向量外積 (cross)

為兩項量構成行四邊形的有向面積

\vec{u} × \vec{v} = |\vec{u}||\vec{v}|sin(\theta)

在計算幾何中，我們如何描述一條線 ?

在計算幾何中，我們如何描述一條線 ?

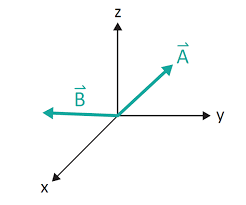
為什麼我們選擇用向量 ?

  • 用方程式可能不好表達一些特殊情況 ex:鉛直線
  • 方程式要用到浮點數
  • 可能很難表達一個線段

為什麼我們選擇用向量 ?

  • 用方程式可能不好表達一些特殊情況 ex:鉛直線
  • 方程式要用到浮點數
  • 可能很難表達一個線段

向量全部都可以 !

用電腦存向量，基本運算

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define maxn 200005
#define endl '\n'
#define X first
#define Y second
typedef pair<int,int> pl;
pl operator+(const pl&a,const pl&b){
    return pl(a.X+b.X,a.Y+b.Y);
}
pl operator-(const pl&a,const pl&b){
    return pl(a.X-b.X,a.Y-b.Y);
}
int operator*(const pl&a,const pl&b){
    return a.X*b.X+a.Y*b.Y;
}
int operator^(const pl&a,const pl&b){
    return a.X*b.Y-a.Y*b.X;
}
int sing(int a){
    return a==0 ? 0 : a>0 ? 1:-1;
}
int ori(pl a,pl b,pl c){
    return sing((b-a)^(c-a));
}

基礎應用 : 計算多邊形有向面積

有一個多邊形，順時針的點依序為

 

 

隨便在找一個點      ，然後算

(a_0,a_1,a_2,a_3 ... ... a_{n-1})
o
\sum_{i=0}^{n-1} \overrightarrow{o a_i}×\overrightarrow{o a_{(i+1)\% n}}

基礎應用 : 計算多邊形有向面積

有一個多邊形，順時針的點依序為

 

 

隨便在找一個點      ，然後算

(a_0,a_1,a_2,a_3 ... ... a_{n-1})
o
\sum_{i=0}^{n-1} \overrightarrow{o a_i}×\overrightarrow{o a_{(i+1)\% n}}

練習看看吧

基礎應用 : 計算多邊形有向面積

這也叫測量師公式、鞋帶公式

\sum_{i=0}^{n-1} \overrightarrow{o a_i}×\overrightarrow{o a_{(i+1)\% n}}

線段相交

a_1
a_2
b_1
b_2

先感性觀察一下當兩個線段相交時有什麼特徵

a_1
a_2
b_1
b_2

先感性觀察一下當兩個線段相交時有什麼特徵

一條線的兩端點在另外一條線的兩端

好像還差了點什麼 ?

a_1
a_2
b_1
b_2

兩線平行

且一點在另一線中

先處理第一部分 : 一條線的兩端點在另外一條線的兩端

a_1
a_2
b_1
b_2
(\overrightarrow{a_1 a_2} × \overrightarrow{a_1 b_1}) \cdot (\overrightarrow{a_1 a_2} × \overrightarrow{a_1 b_2}) < 0 \land
(\overrightarrow{b_1 b_2} × \overrightarrow{b_1 a_1}) \cdot(\overrightarrow{b_1 b_2} × \overrightarrow{b_1 a_2}) < 0

第二部分 : 兩線平行，且一點在另一線中

(\overrightarrow{b_2 a_1} × \overrightarrow{b_2 a_2}) = 0 \land (\overrightarrow{b_2 a_1} • \overrightarrow{b_2 a_2}) <= 0
a_1
a_2
b_1
b_2

寫成程式碼吧 !

pl operator+(const pl&a,const pl&b){
    return pl(a.X+b.X,a.Y+b.Y);
}
pl operator-(const pl&a,const pl&b){
    return pl(a.X-b.X,a.Y-b.Y);
}
int operator*(const pl&a,const pl&b){
    return a.X*b.X+a.Y*b.Y;
}
int operator^(const pl&a,const pl&b){
    return a.X*b.Y-a.Y*b.X;
}
int sing(int a){
    return a==0 ? 0 : a>0 ? 1:-1;
}
int ori(pl a,pl b,pl c){
    return sing((b-a)^(c-a));
}
int btw(pl a,pl b,pl c){
    return ori(a,b,c)==0 && (b-a)*(c-a) <= 0;
}
bool cross(pl a1,pl a2,pl b1,pl b2){
    if(btw(a1,b1,b2) || btw(a2,b1,b2) || btw(b1,a1,a2) || btw(b2,a1,a2)) return true;
    return ori(a1,a2,b1)!=ori(a1,a2,b2) && ori(b1,b2,a1)!=ori(b1,b2,a2);
}

來練習看看吧 

裸題

線段交點

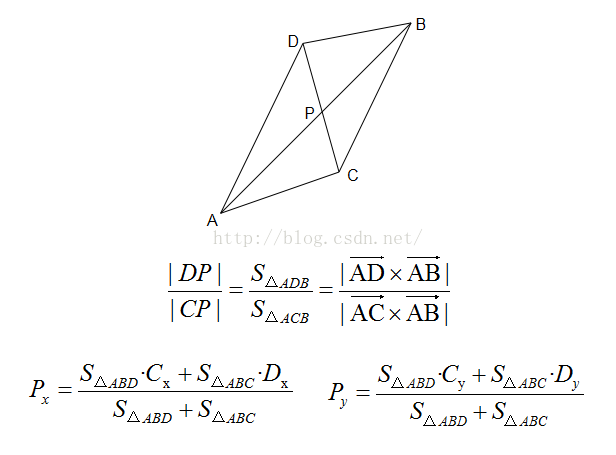
發現如果我可以知道 AP 長度比 PB 長度

就可以用分點公式算出來了

線段交點

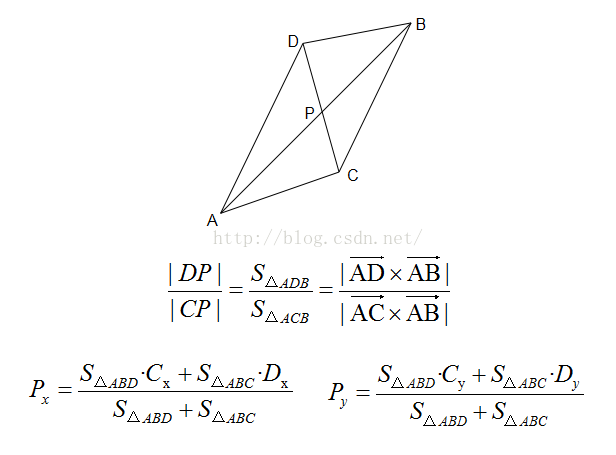
又發現                        、           

\triangle ADC
\triangle DBC

的面積比就是線段的長度比

因此直接算 

\triangle ADC : \triangle DBC

再分點公式即可

點到線段的距離

你可能會想到國中學的點到直線距離公式

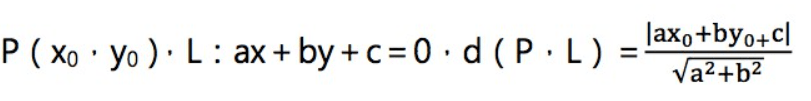
你可能會想到國中學的點到直線距離公式

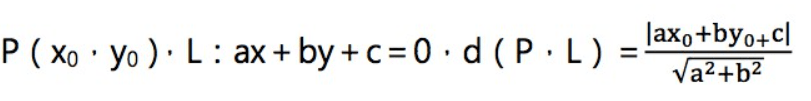
但是有根號，又要除法，一定到用到浮點數，不行 !

你可能會想到國中學的點到直線距離公式

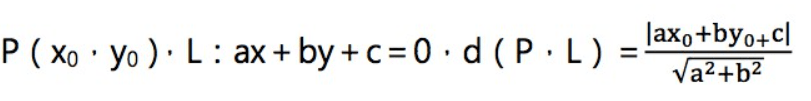
但是有根號，又要除法，一定到用到浮點數，不行 !

我們分成幾種情況討論~

假設我要求點 A 到 BC 線段的距離

case1 : B = C

這樣根本就超簡單，距離就是 

|\overline{AB}|

case2 : A再BC線段投影外

距離是

min(|\overline{AB}|,|\overline{AC}|)

case3 : A再BC線段投影內

B
C
A

發現要求的就是A在BC邊上的高

 

= \frac{|\overrightarrow{AB}×\overrightarrow{AC}|}{|\overrightarrow{BC}|}

但要如何判斷點是否在投影內呢 ?

B
C

觀察看看，其實就是 

\angle{BCA} <= 90° \land \angle{CBA} <= 90°

但要如何判斷點是否在投影內呢 ?

B
C

寫成向量形式 :

\overrightarrow{BA} • \overrightarrow{BC} >= 0 \land \overrightarrow{CA} • \overrightarrow{CB} >= 0
double dis(const pl&a,const pl&b){
    double xx = a.X-b.X, yy = a.Y-b.Y;
    return sqrt(xx*xx+yy*yy);
}
main(){
	int dis;
	if( (p[i]-st)*(p[i]-p[i+1]) < 0 || (p[i+1]-st)*(p[i+1]-p[i]) < 0)
		dis = min(dis(st,p[i]),dis(st,p[i+1]));
	else
		dis = ((double)(abs((st-p[i])^(st-p[i+1]))))/dis(p[i],p[i+1]);
}

寫成程式碼吧

你已經可以在全國賽中寫出一題了 !

練習看看吧

沒那麼裸但還是很裸的題目

極角排序

極角排序是什麼 ?

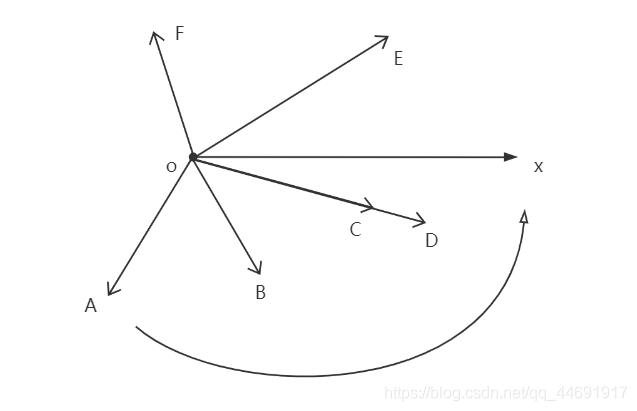
更精確地說就是以一點為中心

將其他點按照較度排序

我們會用與x軸正向，逆時針的角度

方法一 : 直接用內建             排序

tan^{-1}

方法一 : 直接用內建             排序

tan^{-1}

雖然方法最直觀方便，但有許多問題 、缺點

  • 浮點數誤差
  • 排序的順序是從第三象限~第二象限，不直觀
  • 跑的常數大，很慢
bool comp1(const pl &a,const pl&b){
    return atan2(a.Y,a.X) < atan2(b.Y,b.X);
}

atan2(y,x)會回傳弧度      ~

\pi
-\pi

方法二 (推薦使用這個)

因為我們需要知道兩向量的角度關係 .....

方法二 (推薦使用這個)

因為我們需要知道兩向量的角度關係 .....

所以我們可以用外積判，還記得有向面積嗎

方法二 (推薦使用這個)

因為我們需要知道兩向量的角度關係 .....

所以我們可以用外積判，還記得有向面積嗎

\vec{A}
\vec{B}
\vec{A} × \vec{B} < 0
\vec{B} × \vec{A} > 0

為了方便，我們先假設我們選的中心為原點

為了方便，我們先假設我們選的中心為原點

並先把所有點分成在中心點的上/下方

為了方便，我們先假設我們選的中心為原點

並先把所有點分成在中心點的上/下方

為了方便，我們先假設我們選的中心為原點

並先把所有點分成在中心點的上/下方

接下來我們只要考慮上方的就好 (下方作法一模一樣)

我們需要的只有比較函式，也就是

拿到兩個點，回傳是否要交換

接下來我們只要考慮上方的就好 (下方作法一模一樣)

bool comp(const pl &a,const pl&b){
    return //一些判斷式
}

如果回傳true，a、b不會交換

否則會

接下來我們只要考慮上方的就好 (下方作法一模一樣)

\vec{A}
\vec{B}
\vec{A} × \vec{B} < 0
\vec{A} × \vec{B} > 0

換

不換

code

int neg(pt a){
    if(a.Y<o.Y||(a.Y==o.Y&&a.X<o.X)) return 1;
    return 0;
}
bool comp(pt a,pt b){
    int A = neg(a), B = neg(b);
    if(A!=B) return B>A;
    return ((a-o)^(b-o))>0;
}

這裡o為中心點

練習使用一下極角排序

有n個點，請求出所有選三個點圍出三角形面積不為0的方法數

練習用一下極角排序

有n個點，請求出所有選三個點圍出三角形面積不為0的方法數

仔細想想，其實就是全部的方法數扣掉面積是0的嘛

練習用一下極角排序

有n個點，請求出所有選三個點圍出三角形面積不為0的方法數

仔細想想，其實就是全部的方法數扣掉面積是0的嘛

找共線 !

連結

+一些些數學

C
D

code

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define X first
#define Y second
#define maxn 2450
typedef pair<int,int> pt;
pt operator+(const pt&a,const pt&b){
    return pt(a.X+b.X,a.Y+b.Y);
}
pt operator-(const pt&a,const pt&b){
    return pt(a.X-b.X,a.Y-b.Y);
}
int operator*(const pt&a,const pt&b){
    return a.X*b.X+a.Y*b.Y;
}
int operator^(const pt&a,const pt&b){
    return a.X*b.Y-a.Y*b.X;
}
int n,cnt[maxn];
vector<pt> vp;
pt o;
int neg(pt a){
    if(a.Y<o.Y||(a.Y==o.Y&&a.X<o.X)) return 1;
    return 0;
}
bool comp(pt a,pt b){
    int A = neg(a), B = neg(b);
    if(A!=B) return B>A;
    return ((a-o)^(b-o))>0;
}
void cal(int x){
    o = vp[x];
    vector<pt> tmp;
    for(int i=0;i<n;++i){
        if(i==x) continue;
        if(o.Y==vp[i].Y&&o.X<vp[i].X) tmp.push_back(vp[i]);
        else if(vp[i].Y<=o.Y){
            pt d = (o-vp[i]);
            tmp.push_back({o.X+d.X,o.Y+d.Y});
        }
        else tmp.push_back(vp[i]);
    }
    sort(tmp.begin(),tmp.end(),comp);
    int l=0,r=0,len = tmp.size();
    while(r<len-1){
        r = l;
        while(r<=(len-2)&&((tmp[r+1]-o)^(tmp[l]-o))==0) r++;
        cnt[r-l+2]++;
        l = r+1;
    }
}
main(){
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin>>n;
    for(int i=0;i<n;++i){
        int a,b; cin>>a>>b;
        vp.push_back({a,b});
    }
    for(int i=0;i<n;++i) cal(i);
    int as = (n*(n-1)*(n-2))/6;
    for(int i=3;i<=n;++i){
        if(!cnt[i]) continue;
        cnt[i]/=i;
        as -= cnt[i]*(i*(i-1)*(i-2))/6;
    }
    cout<<as<<endl;
    return 0;
}

凸包

凸包是啥 ?

凸包是啥 ?

我也看不懂這是啥

凸包是啥 ?

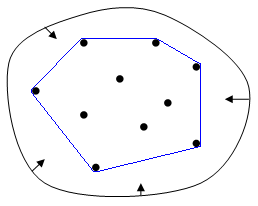
直接感性理解，就是用橡皮筋把點綁起來

也是一個最小的凸多邊形，把所有給的所有點點包住

反正就是給你很多點，求出那些點可以形成把其他點圍起來的最小凸多邊形

有非常多做法，但今天只教最簡單的

 

有非常多做法，但今天只教最簡單的

Monotone Chain

其他的我不會

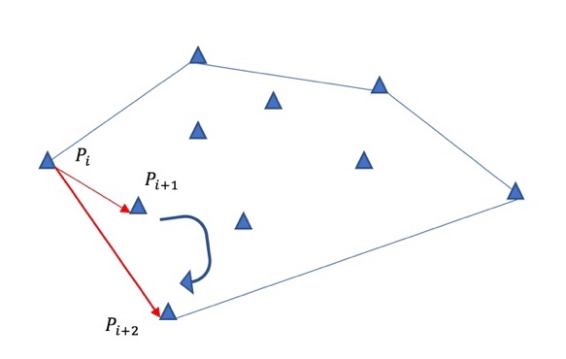
先定義一下 :

最左邊的點屬於下凸包

最右邊的點屬於上凸包

首先，我們先圍出下凸包，也就是:

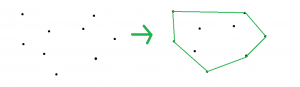
並將所有點的x座標由小到大排序

我們假設我們已經考慮完前 i 個點了

並存於一個陣列中，現在考慮點i+1

我們假設我們已經考慮完前 i 個點了

並存於一個陣列A中，現在考慮點i+1

a_{-1}
a_{-3}
a_{-2}

可以分成紅藍兩種情況

我們假設我們已經考慮完前 i 個點了

並存於一個陣列A中，現在考慮點i+1

a_{-1}
i+1

case1:紅色情況 : 直接將點i+1放進A

a_{-3}
a_{-2}

我們假設我們已經考慮完前 i 個點了

並存於一個陣列A中，現在考慮點i+1

i+1

case2:藍色情況 : 很顯然這樣不像一個凸包

因此將點 a-1 pop掉，然後繼續比較

 

a_{-1}
a_{-3}
a_{-2}

我們假設我們已經考慮完前 i 個點了

並存於一個陣列A中，現在考慮點i+1

那如何判斷哪個case呢?

a_{-1}
a_{-3}
a_{-2}

我們假設我們已經考慮完前 i 個點了

並存於一個陣列A中，現在考慮點i+1

那如何判斷哪個case呢?

看一下

\overrightarrow{a_{-2}a_{-1}}
\overrightarrow{a_{-2}a_{i+1}}

、

的關係即可

a_{-1}
a_{-3}
a_{-2}

我們假設我們已經考慮完前 i 個點了

並存於一個陣列A中，現在考慮點i+1

\overrightarrow{a_{-2}a_{-1}}
\overrightarrow{a_{-2}a_{i+1}}
a_{-1}
a_{-3}
a_{-2}
\times
< 0

為藍色情況

我們圍完下凸包了 !!

接下來就是把點的座標按x從大到小排

並再作一次剛剛的事

我們圍完下凸包了 !!

接下來就是把點的座標按x從大到小排

並再作一次剛剛的事

看個動畫可能比較清楚

看看怎麼實作吧 板子題

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define maxn 200005
#define endl '\n'
#define X first
#define Y second
typedef pair<int,int> pl;
pl operator+(const pl&a,const pl&b){
    return pl(a.X+b.X,a.Y+b.Y);
}
pl operator-(const pl&a,const pl&b){
    return pl(a.X-b.X,a.Y-b.Y);
}
int operator*(const pl&a,const pl&b){
    return a.X*b.X+a.Y*b.Y;
}
int operator^(const pl&a,const pl&b){
    return a.X*b.Y-a.Y*b.X;
}
int sing(int a){
    return a==0 ? 0 : a>0 ? 1:-1;
}
int ori(pl a,pl b,pl c){
    return sing((b-a)^(c-a));
}
int n;
pl p[maxn];
vector<pl> convex_hull(){
    sort(p+1,p+1+n);
    vector<pl> Q;
    for(int t=0;t<2;++t){
        int sz = Q.size();
        for(int i=1;i<=n;++i){
            while((int)Q.size()-sz >= 2 && ori(Q.end()[-2],Q.end()[-1],p[i]) == -1)
                Q.pop_back();
            Q.push_back(p[i]);
        }
        Q.pop_back();
        reverse(p+1,p+1+n);
    }
    return Q;
}
main(){
    ios::sync_with_stdio(0); cin.tie(0);
    cin>>n;
    for(int i=1;i<=n;++i) cin>>p[i].X>>p[i].Y;
    sort(p+1,p+1+n);
    vector<pl> as = convex_hull();
    cout<<as.size()<<endl;
    for(auto i:as) cout<<i.X<<' '<<i.Y<<endl;
}

其他

1、浮點數誤差、eps

電腦的小數是用以2為底的科學記號

1、浮點數誤差、eps

這著叫做 IEEE 754

反正就是規定一些浮點數的規則、運算標準

1、浮點數誤差、eps

每次計算，誤差可能會疊加，因此要特別小心

尤其是減法與除法

1、浮點數誤差、eps

時常算 0.2 + 0.3 == 0.5 會是 false

1、浮點數誤差、eps

時常算 0.2 + 0.3 == 0.5 會是 false

因此如果題目必須用浮點數

我們會設定一個 eps

當兩數差值絕對值 <= eps 就算相等

1、浮點數誤差、eps

時常算 0.2 + 0.3 == 0.5 會是 false

因此如果題目必須用浮點數

我們會設定一個 eps

當兩數差值絕對值 <= eps 就算相等

通常取個

10^{-6}
10^{-9}

~

一些可以體驗浮點數很麻煩的題目 :

我怎麼可能錯這題 !!

???????

所以就是可以不要用

就別用 

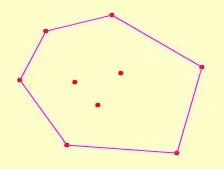
2、判斷一點是否再多邊形內部

題目傳送門

有n個點形成一簡單多邊形，兩兩為多邊形上依序相鄰的點

有m比詢問，每次回答點是否在多邊形內部

2、判斷一點是否再多邊形內部

如果是凸多邊形 ?

2、判斷一點是否再多邊形內部

如果是凸多邊形 ?

就直接檢查，是否每點都位於每條邊的同一邊

2、判斷一點是否再多邊形內部

如果是凹的呢?

2、判斷一點是否再多邊形內部

如果是凹的呢?

壞了QQ

2、判斷一點是否再多邊形內部

如果是凹的呢?

觀察一個性質，就是不管多邊形是凹或凸

一個點往一個方向一直走

2、判斷一點是否再多邊形內部

如果是凹的呢?

觀察一個性質，就是不管多邊形是凹或凸

一個點往一個方向一直走

只要穿過一個邊，就一定會

切換一次在多邊形內還外

(外->內、內->外)

2、判斷一點是否再多邊形內部

因此作法就會是

從點打一個超長的射線往外

再算與多邊形的幾條邊交會到

2、判斷一點是否再多邊形內部

因此作法就會是

從點打一個超長的射線往外

再算與多邊形的幾條邊交會到

奇數次 -> 點在內部

偶數次 -> 點在外部

2、判斷一點是否再多邊形內部

那如果我的射線與其中一個邊重和，或是剛好交在點上怎麼辦...

2、判斷一點是否再多邊形內部

那如果我的射線與其中一個邊重和，或是剛好交在點上怎麼辦...

最簡單的方法就是射線的向量取個

(1,p)

p為一個超大質數，可能是998244353、1000000007 之類的

中場休息

跟計算幾何沒啥關係

Palette

By maxbrucelen

Made with Slides.com

Palette

  • 168

More from maxbrucelen