DP優化
我最近有蒐集了一個分類題單
可能有一兩個分錯對不起
資結優化
單調對列優化
題目概要如下：
-
主街分成
n個區段，編號從 1 到 n，每個相鄰區段距離為 1。 -
總共有
m場煙火，每場煙火會在時間ti、地點ai發射。 -
如果你在時間
ti時位於區段x，那麼這場煙火帶來的快樂值是bi - |ai - x|（離煙火越近快樂值越高，也可能為負）。 -
你可以在單位時間內移動最多
d單位距離（例如從區段 3 到區段 6，如果距離允許是可以做到的）。 -
初始時刻（時間 = 1）可以在任意位置，不能超出主街範圍。
-
你的目標是選擇每個時間點應該站在哪個位置，以最大化總快樂值。
n <= 150000 m <= 300 d <= n
我們可以用DP解決此問題
dp[i][j] 考慮前 i 場煙火，第 i 場煙火開始時正在位置 j
定義 :
我們可以用DP解決此問題
dp[i][j] 考慮前 i 場煙火，第 i 場煙火開始時正在位置 j
dp_{i,j} = max(dp[i-1][k]+b_i-|a_i-j|)
max(1,j-d)<=k<=min(n,j+d)
轉移 :
定義 :
可以發現，如果直接暴力轉移
每次轉移的時間複雜度為
O(n)
因此總時間複雜度就會是
O(nm) \cdot O(n) = O(n^2m)
可以發現，如果直接暴力轉移
每次轉移的時間複雜度為
O(n)
因此總時間複雜度就會是
O(nm) \cdot O(n) = O(n^2m)
TLE
可以發現，其實每次轉移時
轉移來源都是一個左右端都單調向右的區間
dp_{i,j} = max(dp[i-1][k]+b_i-|a_i-j|)
可以發現，其實每次轉移時
轉移來源都是一個左右端都單調向右的區間
dp_{i,j} = max(dp[i-1][k]+b_i-|a_i-j|)
而我們要找的其實就是這個區間的最大值
因此你就可以用任何可以求出區間極值的資結
ex : 線段樹 、 ST表 、 treap 、 單調對列
因此你就可以用任何可以求出區間極值的資結
ex : 線段樹 、 ST表 、 treap 、 單調對列
但在符合區間移動式單調的情況下，用單調對列可以少一個 log
因此你就可以用任何可以求出區間極值的資結
ex : 線段樹 、 ST表 、 treap 、 單調對列
但在符合區間移動式單調的情況下，用單調對列可以少一個 log
總時間複雜度 :
O(nm)
Watching Fireworks is Fun AC code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 150005
#define inf 1e18
struct qus{
int a,b,t;
};
qus Q[305];
int n,m,d,dp[maxn][2];
main(){
ios::sync_with_stdio(0); cin.tie(0);
cin>>n>>m>>d;
for(int i=1;i<=m;++i){
cin>>Q[i].a>>Q[i].b>>Q[i].t;
}
for(int i=1;i<=n;++i){
dp[i][1] = Q[1].b - abs(Q[1].a-i);
}
deque<int> dq;
for(int i=2;i<=m;++i){
int mxd = (Q[i].t-Q[i-1].t)*d;
while(!dq.empty()) dq.pop_back();
for(int j=1;j<=n;++j){
int R = min(n,j+mxd);
int L = max(1ll,j-mxd);
int pos = (dq.empty())?0:dq.back();
while(pos < R){
pos++;
while(!dq.empty() && dp[dq.back()][(i+1)%2] <= dp[pos][(i+1)%2]) dq.pop_back();
dq.push_back(pos);
}
while(!dq.empty() && dq.front() < L) dq.pop_front();
dp[j][i%2] = dp[dq.front()][(i+1)%2]+Q[i].b-abs(Q[i].a-j);
}
}
int mx = -inf;
for(int i=1;i<=n;++i) mx = max(mx,dp[i][m%2]);
cout<<mx<<endl;
}總結來說，就是當你在轉移時
如果發現轉移來源是一個單調移動的區間
那麼可以用單調對列優化
做到每次均攤 O(1) 轉移
總結來說，就是當你在轉移時
如果發現轉移來源是一個單調移動的區間
那麼可以用單調對列優化
做到每次均攤 O(1) 轉移
如果沒有單調移動 ?
總結來說，就是當你在轉移時
如果發現轉移來源是一個單調移動的區間
那麼可以用單調對列優化
做到每次均攤 O(1) 轉移
如果沒有單調移動 ?
多花一個 log 用線段樹
線段樹(有時候BIT也可以)優化
線段樹優化
(其實我也不知道有沒有這個專有名詞)
高橋計畫參加 N 場 AtCoder 比賽。
-
在第
i場比賽中，如果他的評分（rating）在區間[L_i, R_i]之內（包含端點），他的評分會 增加 1 分。 -
否則，這場比賽不會讓他的評分改變。
你會接到 Q 個查詢，每個查詢都給你一個整數 X，代表高橋的初始評分，請你輸出他在參加完所有 N 場比賽後的最終評分。
n <= 2e5 x <= 5e5 Q<=3e5
首先這題很壞，他用詢問的方式，所以能
不會往DP的方面想
其實只要知道是DP後就沒那麼難了
定義 :
dp[i][j] = 經過了前 i 場比賽
如果初始等級為 j ，現在會是幾等
轉移 :
dp[i][j] =
\begin{cases}
dp[i-1][j] + 1 & \text{if } L_i \le dp[i-1][j] \le R_i \\
dp[i-1][j] & \text{otherwise}
\end{cases}
dp[i][j] =
\begin{cases}
dp[i-1][j] + 1 & \text{if } L_i \le dp[i-1][j] \le R_i \\
dp[i-1][j] & \text{otherwise}
\end{cases}
如果暴力轉移，雖然每次轉移為
O(1)
但狀態數量有
O(n \cdot max(x_i))
MLE + TLE
連空間都不夠了，怎麼辦 ??
連空間都不夠了，怎麼辦 ??
不要一次把整個DP表都開出來 !
如果改成滾動DP，就可以解決空間不足的問題了
但是時間複雜度還是一樣
可以觀察到對於每層的轉移
例如從 dp[i-1] -> dp[i]
會變化 (+1) 的地方會是一個連續區間
因此我們可以用支援區快速
區間加值的資料結構優化
可以觀察到對於每層的轉移
例如從 dp[i-1] -> dp[i]
會變化 (+1) 的地方會是一個連續區間
因此我們可以用支援區快速
區間加值的資料結構優化
線段樹 !
初始時，這顆線段樹代表 dp[0]
每次轉移我們就只要找到線段樹中
那些位置的值，是介於 L~R 就好
初始時，這顆線段樹代表 dp[0]
每次轉移我們就只要找到線段樹中
那些位置的值，是介於 L~R 就好
會發現因為整個線段樹的數值是非嚴格遞增
因此這些位置會是連續的
初始時，這顆線段樹代表 dp[0]
每次轉移我們就只要找到線段樹中
那些位置的值，是介於 L~R 就好
會發現因為整個線段樹的數值是非嚴格遞增
因此這些位置會是連續的
因此找到這個區間後就進行區間加值即可
最後的線段樹，就是 dp[n]
位置 i 就代表初始等級 i
經過 n 場比賽後等級為何
由於要進行的是單點查詢
因此也可以用 bit + 差分做到
由於要進行的是單點查詢
因此也可以用 bit + 差分做到
缺點是會多一個 log
(找區間的時候要二分搜)
F - Rated Range AC code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 1e18
#define endl '\n'
#define maxn 1000006
int n,bit[maxn],q;
pair<int,int> p[maxn];
int lb(int x){
return x&(-x);
}
void modify(int x,int v){
for(int i=x;i<maxn;i+=lb(i)) bit[i] += v;
}
int query(int x){
int sum = 0;
for(int i=x;i;i-=lb(i)) sum += bit[i];
return sum;
}
main(){
ios::sync_with_stdio(0); cin.tie(0);
cin>>n;
for(int i=1;i<=n;++i) cin>>p[i].first>>p[i].second;
for(int i=1;i<=500005;++i) modify(i,i),modify(i+1,-i);
for(int i=1;i<=n;++i){
int L,R,l=0,r = 500005,mid;
while(l+1<r){
mid = (l+r)/2;
if(query(mid) >= p[i].first) r = mid;
else l = mid;
}
L = r;
l = 0,r = 500005;
while(l+1<r){
mid = (l+r)/2;
if(query(mid) > p[i].second) r = mid;
else l = mid;
}
R = r;
modify(L,1);
modify(R,-1);
}
cin>>q;
while(q--){
int x; cin>>x;
cout<<query(x)<<endl;
}
}
矩陣快速冪優化
如果要你求費是數列第n項你會嗎?
如果要你求費是數列第n項你會嗎?
直接暴力dp! -> O(n)
如果要你求費是數列第n項你會嗎?
直接暴力dp! -> O(n)
如果我說 呢 ?
n <= 10^{18}
以目前的方法，每次轉移最快就O(1)吧?
如何優化
其實一個遞迴式的轉移可以用矩陣表達!
其實一個遞迴式的轉移可以用矩陣表達!
以費氏數列為例 :
dp_i = dp_{i-1} + dp_{i-2}
表示成矩陣就是 :
其實一個遞迴式的轉移可以用矩陣表達!
以費氏數列為例 :
dp_i = dp_{i-1} + dp_{i-2}
表示成矩陣就是 :
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{i-1} \\
dp_{i-2}
\end{bmatrix}
=
\begin{bmatrix}
dp_{i} \\
dp_{i-1}
\end{bmatrix}
因此如果我想算 :
dp_4
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{1} \\
dp_{0}
\end{bmatrix}
=
\begin{bmatrix}
dp_{2} \\
dp_{1}
\end{bmatrix}
因此如果我想算 :
dp_4
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{1} \\
dp_{0}
\end{bmatrix}
=
\begin{bmatrix}
dp_{2} \\
dp_{1}
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{2} \\
dp_{1}
\end{bmatrix}
=
\begin{bmatrix}
dp_{3} \\
dp_{2}
\end{bmatrix}
因此如果我想算 :
dp_4
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{1} \\
dp_{0}
\end{bmatrix}
=
\begin{bmatrix}
dp_{2} \\
dp_{1}
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{2} \\
dp_{1}
\end{bmatrix}
=
\begin{bmatrix}
dp_{3} \\
dp_{2}
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{3} \\
dp_{2}
\end{bmatrix}
=
\begin{bmatrix}
dp_{4} \\
dp_{3}
\end{bmatrix}
展開就是 :
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{1} \\
dp_{0}
\end{bmatrix}
=
\begin{bmatrix}
dp_{4} \\
dp_{3}
\end{bmatrix}
展開就是 :
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
^3
\cdot
\begin{bmatrix}
dp_{1} \\
dp_{0}
\end{bmatrix}
=
\begin{bmatrix}
dp_{4} \\
dp_{3}
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\cdot
\begin{bmatrix}
dp_{1} \\
dp_{0}
\end{bmatrix}
=
\begin{bmatrix}
dp_{4} \\
dp_{3}
\end{bmatrix}
觀察一下可以發現，如我我要求陣列的第 n 項 :
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
^{n-1}
\cdot
\begin{bmatrix}
dp_{1} \\
dp_{0}
\end{bmatrix}
=
\begin{bmatrix}
dp_{n} \\
dp_{n-1}
\end{bmatrix}
接下來要解決的就是如何快速計算
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
^{n-1}
接下來要解決的就是如何快速計算
\begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
^{n-1}
快速冪 !
為什麼矩陣可以快速冪呢?
為什麼矩陣可以快速冪呢?
因為矩陣乘法具有結合律
A \cdot (B \cdot C) = (A\cdot B)\cdot C
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int p = 1000000007;
struct matrix{
int v[2][2];
matrix(int t){
for(int i=0;i<2;++i)for(int j=0;j<2;++j) v[i][j] = 0;
for(int i=0;i<2;++i) v[i][i] = t;
}
};
matrix mul(matrix a,matrix b){
matrix c{0};
for(int i=0;i<2;++i){
for(int k=0;k<2;++k){
for(int j=0;j<2;++j){
c.v[i][k] += (a.v[i][j]*b.v[j][k]);
c.v[i][k] %= p;
}
}
}
return c;
}
matrix power(matrix x,int y){
matrix res{1};
while(y){
if(y&1) res = mul(res,x);
x = mul(x,x);
y >>= 1;
}
return res;
}
int n;
main(){
matrix org{1};
org.v[0][0] = 1;
org.v[1][0] = 1;
org.v[0][1] = 1;
org.v[1][1] = 0;
cin>>n;
if(n<=1){
cout<<n<<endl;
return 0;
}
matrix res = power(org,n-1);
cout<<res.v[0][0]<<endl;
return 0;
}
總結 :
總結 :
當我們看到題目要求的東西是做
1e9 ~ 1e18
次某種操作等，可以將轉移式表示為矩陣的
就可以用矩陣快速冪優化
練習題 :
比較不一樣的例子 : 數路徑
給定一張n點m邊圖，求有幾條路徑長度為K
(不用是簡單路徑)
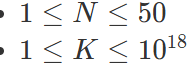
定義:
dp_{i,j,k} =
從 i 走到 j ，長度為k的路徑數量
E_{i,j} = 0 \ or \ 1
表示是i,j間否有邊
定義:
dp_{i,j,k} =
從 i 走到 j ，長度為k的路徑數量
E_{i,j} = 0 \ or \ 1
表示是i,j間否有邊
dp_{i,j,k} =
\begin{cases}
\displaystyle \sum_{t} (dp_{i,t,k/2} \cdot dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \sum_{t} (dp_{i,t,k-1} \cdot E_{t,j}), & \text{otherwise }
\end{cases}
轉移:
dp_{i,j,k} =
\begin{cases}
\displaystyle \sum_{t} (dp_{i,t,k/2} \cdot dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \sum_{t} (dp_{i,t,k-1} \cdot E_{t,j}), & \text{otherwise }
\end{cases}
再走一步
先走k-1步
先走k/2步
再走k/2步
dp_{i,j,k} =
\begin{cases}
\displaystyle \sum_{t} (dp_{i,t,k/2} \cdot dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \sum_{t} (dp_{i,t,k-1} \cdot E_{t,j}), & \text{otherwise }
\end{cases}
再走一步
先走k-1步
先走k/2步
再走k/2步
因為是方法數，所以用乘的 !
dp_{i,j,k} =
從 i 走到 j ，長度為k的路徑數量
答案就是 k = K 時整個dp表格的和
dp_{i,j,k} =
從 i 走到 j ，長度為k的路徑數量
答案就是 k = K 時整個dp表格的和
發現其實 根本就是E
dp_{i,j,1}
因此其實要求的就是
E^K
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 55
#define inf 1e18
#define endl '\n'
const int p = 1000000007;
int n,k;
struct mat{
int v[maxn][maxn];
mat(){
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) v[i][j] = 0;
}
};
mat mul(const mat&a,const mat&b){
mat tmp;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
for(int t=1;t<=n;++t){
tmp.v[i][j] += a.v[i][t]*b.v[t][j];
tmp.v[i][j] %= p;
}
}
}
return tmp;
}
mat power(mat x,int y){
mat res = x;
while(y>0){
if(y&1) res = mul(res,x);
x = mul(x,x);
y >>= 1;
}
return res;
}
main(){
ios::sync_with_stdio(0); cin.tie(0);
cin>>n>>k;
mat dp;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
cin>>dp.v[i][j];
}
}
mat res = power(dp,k-1);
int as = 0;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
as = (as+res.v[i][j])%p;
}
}
cout<<as<<endl;
}
廣義矩陣乘法
C_{i,j} = \sum_k A_{i,k} \cdot B_{k,j}
我們將矩陣運算定義成 :
C_{i,j} = ⊕_k A_{i,k} ⊗ B_{k,j}
剛剛所看到的都是 ⊕ : + ， ⊗ : X
但是其實我們可以任意變換這兩個的定義
但要符合矩陣運算有結合律
就結果來說
⊗要對⊕有分配律
⊕ 要有交換律
⊗ 要有結合律
但是其實我們可以任意變換這兩個的定義
但要符合矩陣運算有結合律
就結果來說
⊗要對⊕有分配律
⊕ 要有交換律
⊗ 要有結合律
但是其實我們可以任意變換這兩個的定義
但要符合矩陣運算有結合律
直接看題目吧!
給定一張n點m邊無向圖，有邊權
我要求出從 i 走到 j 經過邊的數量為 K
的最短路徑
點我不會有題目哈哈哈 因為我找不到
定義:
dp_{i,j,k}=
從 i 走到 j 經過 k 條邊的最短路徑長度
定義:
dp_{i,j,k}=
從 i 走到 j 經過 k 條邊的最短路徑長度
轉移:
dp_{i,j,k} =
\begin{cases}
\displaystyle \min_{t} (dp_{i,t,k/2} + dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \min_{t} (dp_{i,t,k-1} + E_{t,j}), & \text{otherwise }
\end{cases}
dp_{i,j,k} =
\begin{cases}
\displaystyle \min_{t} (dp_{i,t,k/2} + dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \min_{t} (dp_{i,t,k-1} + E_{t,j}), & \text{otherwise }
\end{cases}
⊕ : min ⊗ : +
dp_{i,j,k} =
\begin{cases}
\displaystyle \min_{t} (dp_{i,t,k/2} + dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \min_{t} (dp_{i,t,k-1} + E_{t,j}), & \text{otherwise }
\end{cases}
⊕ : min ⊗ : +
min 對 + 有分配律嗎 ?
dp_{i,j,k} =
\begin{cases}
\displaystyle \min_{t} (dp_{i,t,k/2} + dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \min_{t} (dp_{i,t,k-1} + E_{t,j}), & \text{otherwise }
\end{cases}
⊕ : min ⊗ : +
min 對 + 有分配律嗎 ?
a+min(b,c) = min(a+b,a+c)
有!
dp_{i,j,k} =
\begin{cases}
\displaystyle \min_{t} (dp_{i,t,k/2} + dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \min_{t} (dp_{i,t,k-1} + E_{t,j}), & \text{otherwise }
\end{cases}
⊕ : min ⊗ : +
min 有交換律嗎?
有!
min(a,b) = min(b,a)
dp_{i,j,k} =
\begin{cases}
\displaystyle \min_{t} (dp_{i,t,k/2} + dp_{t,j,k/2}), & \text{if } k \equiv 0 \pmod{2} \\
\displaystyle \min_{t} (dp_{i,t,k-1} + E_{t,j}), & \text{otherwise }
\end{cases}
⊕ : min ⊗ : +
+ 有結合律嗎?
有!
a+(b+c) = (a+b)+c
開始快樂矩陣快速冪吧 !!
斜率優化
簡單說就是把轉移點想像成一條直線
然後進行優化
直接看例題
你正在玩一個有 nnn 個關卡的遊戲，每一關都有一隻怪物。在第 1 到第 n−1n-1n−1 關，你可以選擇擊殺或逃跑。
但在第 nnn 關，你必須擊殺最終魔王才能贏得遊戲。
擊殺一隻怪物所需的時間為 s×fs \times fs×f，其中 sss 是怪物的強度，fff 是你的技能因子（技能因子越小表示技術越好，擊殺時間越短）。
每當你成功擊殺一隻怪物，就會獲得一個新的技能因子。
請問，在最終關擊敗魔王並通關的前提下，最少需要多少時間？
定義 :
dp[i] = 考慮前 i 隻怪物
殺死第 i 隻怪物的最短時間
定義 :
dp[i] = 考慮前 i 隻怪物
殺死第 i 隻怪物的最短時間
轉移 :
dp_i = min(dp_j + f_j \cdot s_i)
j < i
dp_i = min(dp_j + f_j \cdot s_i)
j < i
這個式子，是不是有點像 ...
dp_i = min(dp_j + f_j \cdot s_i)
j < i
這個式子，是不是有點像 ...
ax+b
dp_i = min(dp_j + f_j \cdot s_i)
j < i
我們可以把一個轉移點看成一條直線 !
dp_i = min(dp_j + f_j \cdot s_i)
j < i
我們可以把一個轉移點看成一條直線 !
這次的轉移等價要在所有直線中，找到與直線 的最低交點
(所有直線是指對於所有小於 i 的 j 所對應的直線
x = s_i
y = dp_j + f_jx
x = s_i
x = s_i
轉換完了，然後呢 ?
發現這邊的側資限制有點奇怪
s 非嚴格遞增
f 非嚴格遞減
根據這兩件事情，我們發現
可以用單調對列 !
根據這兩件事情，我們發現
可以用單調對列 !
原因是 :
設直線 L1、L2
如果 L2 斜率比 L1 小
並且 L2 與 x = s (詢問直線) 的交點比 L1 的交點好 (較低)
那麼 L1 就廢了 (之後 L2 一定比 L1 好)
根據這兩件事情，我們發現
可以用單調對列 !
原因是 :
設直線 L1、L2
如果 L2 斜率比 L1 小
並且 L2 與 x = s (詢問直線) 的交點比 L1 的交點好 (較低)
那麼 L1 就廢了 (之後 L2 一定比 L1 好)
而且 f 非嚴格遞減
因此新的線斜率 <= 舊的線
對於每個詢問點的最佳轉移點
會形成一個上凸包
我們在單調對列中保留
還留在上凸包中的直線，
並且以後還有用的直線
因為斜率單調下降
因此組成這個上凸包的
線段所屬直線從左到右，編號也一定是上升
因為斜率單調下降
因此組成這個上凸包的
線段所屬直線從左到右，編號也一定是上升
紅色線段所屬直線編號 > 藍色
放大一點..
一但詢問超過此交點
紅色的轉移點永遠都會比藍色好
因此可以把藍色丟掉!
一但詢問超過此交點
紅色的轉移點永遠都會比藍色好
因此可以把藍色丟掉!
轉移時，我們從單調對列的前面開始看，
對於此次詢問，如果第二條線(轉移點)較第一條線好
則我們可以知道永遠都會如此
轉移時，我們從單調對列的前面開始看，
對於此次詢問，如果第二條線(轉移點)較第一條線好
則我們可以知道永遠都會如此
因此把第一條線 pop 掉
轉移時，我們從單調對列的 front 開始看，
對於此次詢問，如果第二條線(轉移點)較第一條線好
則我們可以知道永遠都會如此
因此把第一條線 pop 掉
一直做，最後的front就會是最佳的線了
講完了詢問，接下來是更新
因為單調對列裡面是要存屬於上凸包的線
因此我們假設目前單調對列是好的
現在正要放入一條新線
黃色是目前單調對列的最後一條
藍色倒數第二條
以下定義 :
黃線 : L-1
藍線 : L-2
當我們加入一條新線 Li
我們可以分兩種情況考慮
此時發現三條線都在禿包上!
若發現三條線都在禿包上!
直接將 Li 放入單調對列
若發現 Li, L-2 合力將 L-1給幹掉
L-1 不再屬於上禿包
若發現 Li, L-2 合力將 L-1給幹掉
L-1 不再屬於上禿包
將 L-1 pop 掉
可以這樣維護也是因為斜率遞減的限制喔!
Monster Game I
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define maxn 200005
#define endl '\n'
#define inf 1e18
struct lines{
int a,b;
lines(){
a = 0,b = 0;
}
};
int n,x,dp[maxn],s[maxn],f[maxn];
lines p[maxn];
bool chack(int L1,int L2,int Ln){
return (p[L2].b-p[L1].b)*(p[L1].a-p[Ln].a) >= (p[Ln].b-p[L1].b)*(p[L1].a-p[L2].a);
}
inline int cal(int id,int x){
return p[id].a*x+p[id].b;
}
main(){
ios::sync_with_stdio(0); cin.tie(0);
cin>>n>>x;
for(int i=1;i<=n;++i) dp[i] = inf;
for(int i=1;i<=n;++i) cin>>s[i];
for(int i=1;i<=n;++i) cin>>f[i];
p[0].a = x;
deque<int> Q;
Q.push_back(0);
for(int i=1;i<=n;++i){
while((int)Q.size()>=2 && cal(Q[0],s[i]) > cal(Q[1],s[i])) Q.pop_front();
dp[i] = cal(Q.front(),s[i]);
p[i].a = f[i];
p[i].b = dp[i];
while((int)Q.size()>=2 && chack(Q.end()[-2],Q.end()[-1],i)) Q.pop_back();
Q.push_back(i);
}
cout<<dp[n]<<endl;
}練習題 :
如果斜率、詢問不是單調的呢?
你正在玩一個有 nnn 個關卡的遊戲，每一關都有一隻怪物。在第 1 到第 n−1n-1n−1 關，你可以選擇擊殺或逃跑。
但在第 nnn 關，你必須擊殺最終魔王才能贏得遊戲。
擊殺一隻怪物所需的時間為 s×fs \times fs×f，其中 sss 是怪物的強度，fff 是你的技能因子（技能因子越小表示技術越好，擊殺時間越短）。
每當你成功擊殺一隻怪物，就會獲得一個新的技能因子。
請問，在最終關擊敗魔王並通關的前提下，最少需要多少時間？
斜率優化就是要找到轉移點所代表的直線的凸包
所以我們只要有一個方法可以有以下操作 :
1 : 加入一條直線
2 : 詢問 x = q 與所有直線的最低交點高度
可以用動態凸包or李超線段樹
可以用動態凸包or李超線段樹
但是因為動態凸包難寫常數又大，所以這邊就不提了
可以用動態凸包or李超線段樹
但是因為動態凸包難寫常數又大，所以這邊就不提了
真正原因是我不會
接下來講解的李超線段樹為
取所有直線的最低交點 (最高也可)
首先我們對值域開一棵線段樹
每個點存的資訊為 :
把所有直線代入 mid，最小的那條線
Ex :
L
R
mid
A
B
L
R
mid
此節點會存下B線
A
B
L
R
mid
A
B
那麼A線去哪裡呢，難道A線沒用了嗎?
L
R
mid
A
B
那麼A線去哪裡呢，難道A線沒用了嗎?
由於A線斜率 < B線，因此A線在右邊可能還有用 !
L
R
mid
A
B
在往右的某個節點中，A線就會比B線好
(某個點的mid)
因此我們新增一條直線時
就是帶著新增的那條線從根節點往下更新
因此我們新增一條直線時
就是帶著新增的那條線從根節點往下更新
然後依照剛剛的方式，如果新的線比原本點上的線好，就更新上去，接著拿點上原本的線繼續往下更新
因此我們新增一條直線時
就是帶著新增的那條線從根節點往下更新
然後依照剛剛的方式，如果新的線比原本點上的線好，就更新上去，接著拿點上原本的線繼續往下更新
否則新線繼續往下更新
只要維護好每個節點的資訊即可!
維護了這些資訊，要如何使用呢 ?
L
R
mid
A
B
如果A線被B線取代 (節點存的線)
並且 A 往右繼續更新，就代表A線在左邊一定沒用
因此查詢的方法非常簡單，我們只需要從根開始
一路走到目標的葉節點，把經過的節點上所存的線
全部都算一次，再從中取最小者即可
李超線段樹模板
struct line{
int a,b;
line():a(0),b(inf){}
line(int c,int d){
a = c;
b = d;
}
int operator()(const int x){
return a*x+b;
}
};
line tree[1000006*4];
void insert(int l,int r,int x,line L){
int ls = x*2, rs = ls+1, mid = (l+r)/2;
if(L(mid) < tree[x](mid)) swap(L,tree[x]);
if(L.a == tree[x].a || l==r) return;
if(L.a > tree[x].a) insert(l,mid,ls,L);
else insert(mid+1,r,rs,L);
}
int query(int a,int l,int r,int x){
int ls = x*2, rs = ls+1, mid = (l+r)/2;
int res = tree[x](a);
if(l==r) return res;
if(mid >= a) res = min(res,query(a,l,mid,ls));
else res = min(res,query(a,mid+1,r,rs));
return res;
}如果要查詢的範圍超大呢，
李超的空間複雜度是 O(詢問值域) ㄟ
如果要查詢的範圍超大呢，
李超的空間複雜度是 O(詢問值域) ㄟ
動態開點!
動態開點李超線段樹模板
struct line{
int a,b;
line(int c,int d){
a = c;
b = d;
}
line():a(0),b(inf){}
int operator()(int x){
return x*a+b;
}
};
struct node{
node *ls,*rs;
line le;
node(){
ls = rs = nullptr;
}
};
void insert(int l,int r,line L,node *now){
int m = (l+r)/2;
if(L(m) < now->le(m)) swap(L,now->le);
if(l==r) return;
if(L.a > now->le.a){
if(now->ls == nullptr) now->ls = new node;
insert(l,m,L,now->ls);
}else{
if(now->rs == nullptr) now->rs = new node;
insert(m+1,r,L,now->rs);
}
}
int query(int l,int r,node *now,int k){
if(now==nullptr) return inf;
if(l==r) return now->le(k);
int m = (l+r)/2;
if(m>=k) return min(now->le(k),query(l,m,now->ls,k));
else return min(now->le(k),query(m+1,r,now->rs,k));
}
關於至轉移點性質的優化
未完待續
DP優化
By maxbrucelen
