\( \text{Agenda of this Lecture:}\)

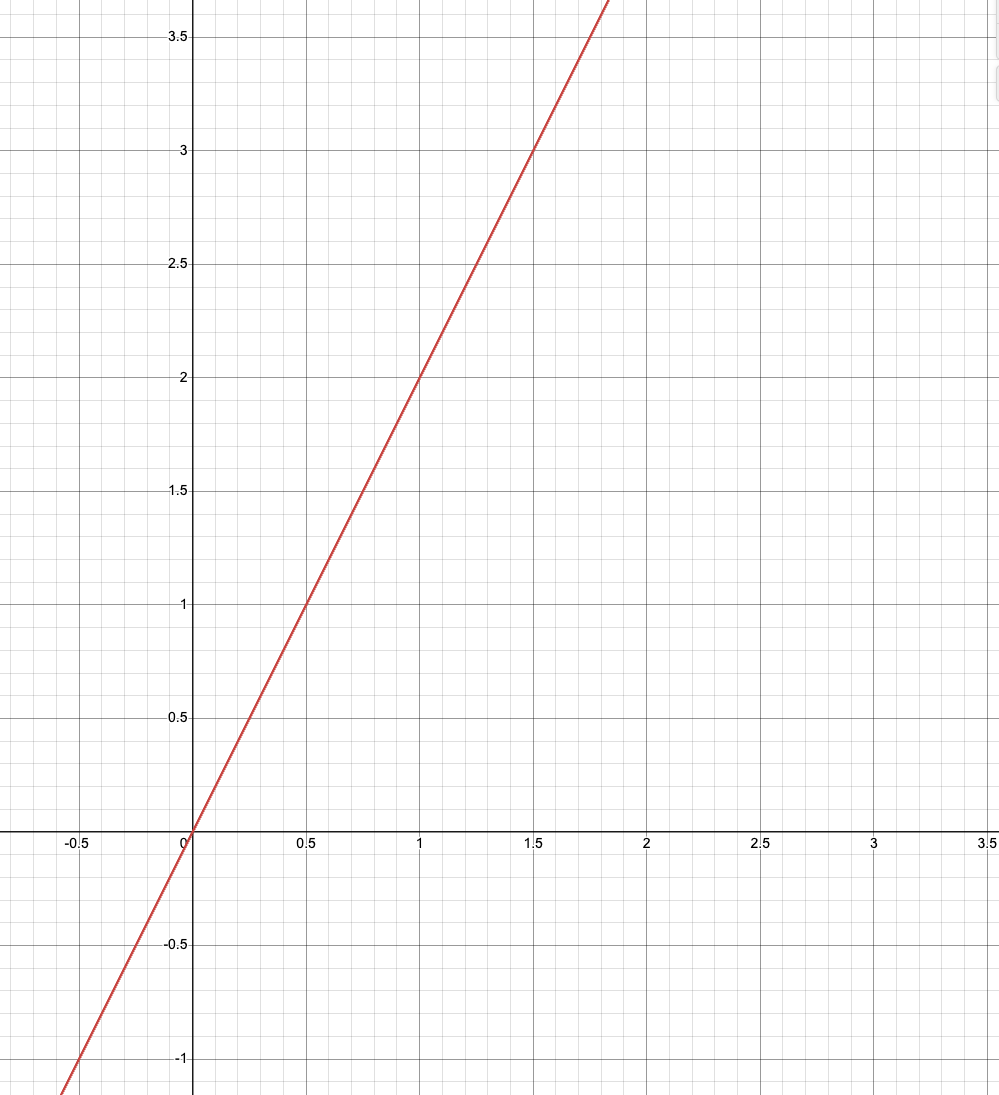
Let's say you are given a bunch of data points:

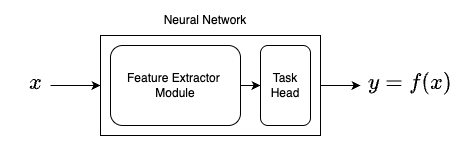
Neural Networks have two components:

• Feature Extractor Module
• Task specific head

You can experiment with simple neural networks at Tensorflow Playground

Usually extracted features are of

lower dimension than data (x)

A simple example of a Neural Network

We have very powerful discriminator models:

• E.g., Image classification models

What about generative models?

Given a label (e.g., "cat"), can we

generate a data point (image)?

Line Fit

Heads

Tails

What can we expect about the outcome?

In probability theory, the law of large numbers is a mathematical law that states that the average of the results obtained from a large number of independent random samples converges to the true value.

Let \(X_1,X_2,\dots\) be independent and identically distributed random variables with finite mean \(\mu=\mathbb{E}[X_1]\).

Define the sample average:

\( \mu \) be the true mean. Then according to the law: 

\( \text{class 0}\)

\( \text{class 1}\)

Decision Boundary

Where does the data come from?

Interpolation for data generation

Can I interpolate between data points?

Basic idea behind morphing images, style mixing, data augmentation

What is the Data Distribution?

What is a Probability Distribution?

A probability distribution describes how the probability mass (discrete) or probability density (continuous) is assigned to different possible outcomes of a random variable.

For a discrete variable X:

For a continuous variable X with PDF \( p(x) \):

What is a Probability Distribution?

• \( p_\theta(x)\) : probability density or mass function parameterized by \( \theta \).
• \( f_\theta(x) \) : energy function or negative log probability
• \( Z_\theta \) : partition function (normalization constant) that ensures the total probability integrates or sums to 1.

Why is it important to estimate a probability distribution?

Mean - \( \mu \)

Variance - \( \sigma^2 \)

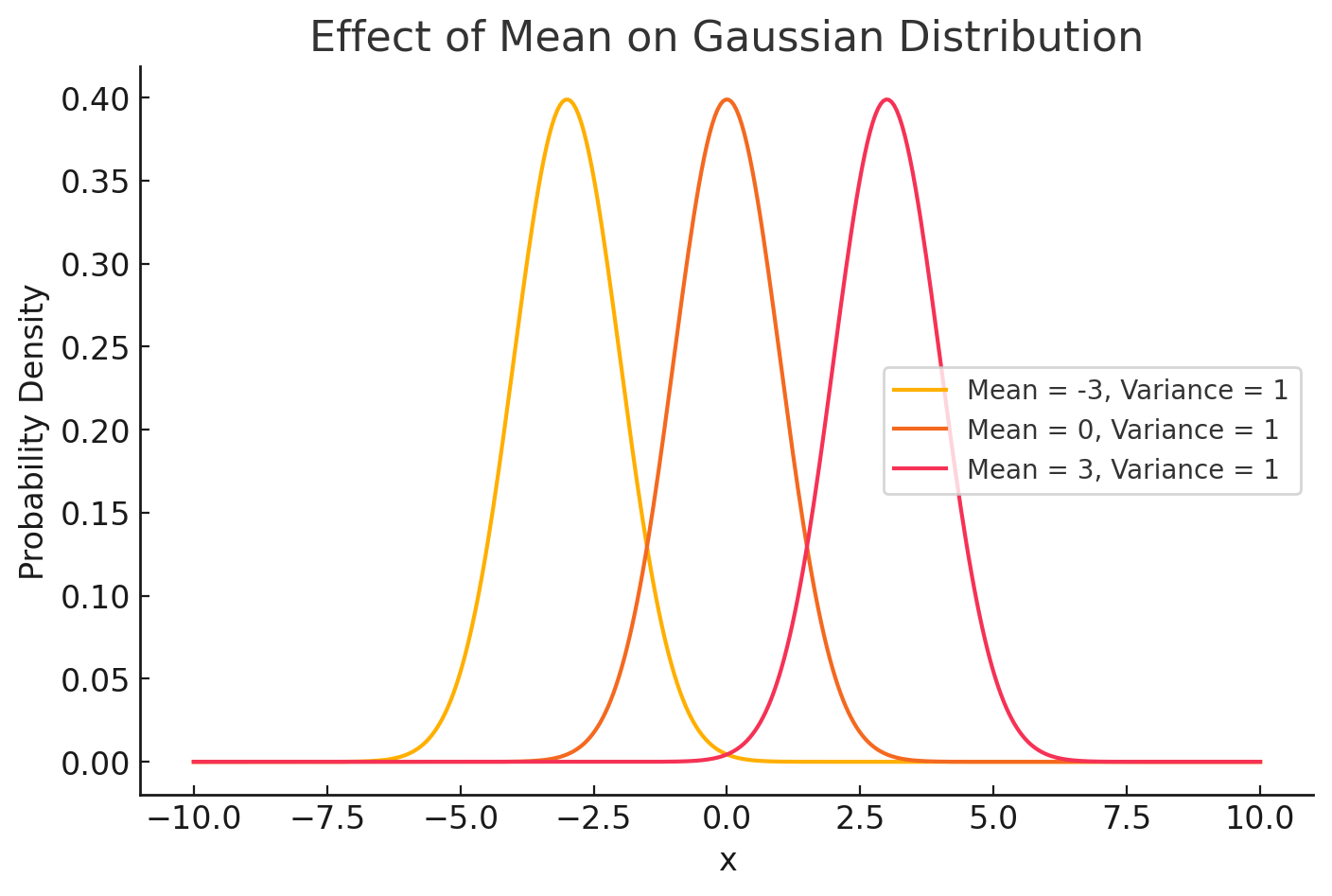
Variance - \( \sigma^2 \)

change

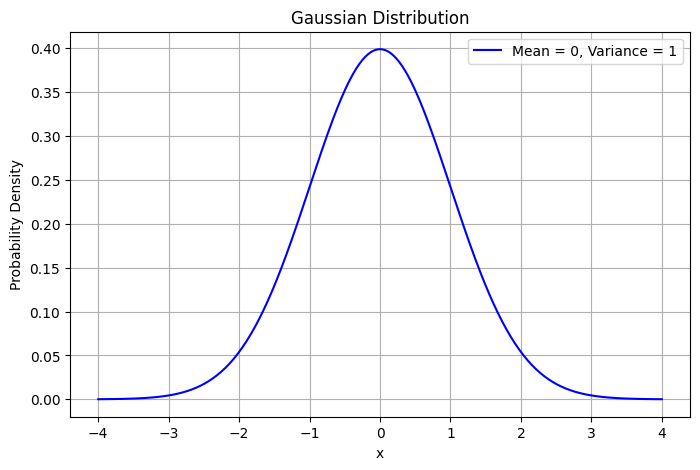
Mean - \( \mu \)

Mean - \( \mu \)

Variance - \( \sigma^2 \)

change

Mean - \( \mu \)

Variance - \( \sigma^2 \)

\( x \) follows a normal distribution with mean \( \mu \) and variance \( \sigma^2 \)

Mean - \( \mu \)

Variance - \( \sigma^2 \)

All of these denote Gaussian distributions

A sample from the above distribution:

Suppose \( x_1 \sim \mathcal{N}(\mu_1, \sigma_1^2 I) \) and \( x_2 \sim \mathcal{N}(\mu_2, \sigma_2^2 I) \).

What is the distribution of \( x_1 + x_2 \)?

Suppose \( \boldsymbol{\varepsilon}_1, \boldsymbol{\varepsilon}_2 \sim \mathcal{N}(0, I) \), and

\( \boldsymbol{x}_1 = \sigma_1 \boldsymbol{\varepsilon}_1 \quad \text{and} \quad \boldsymbol{x}_2 = \sigma_2 \boldsymbol{\varepsilon}_2 \)

\( \boldsymbol{x}_1 + \boldsymbol{x}_2 \sim \mathcal{N}(0, (\sigma_1^2 + \sigma_2^2)I) \).

\( \boldsymbol{x}_1 + \boldsymbol{x}_2 = \sqrt{\sigma_1^2 + \sigma_2^2} \, \boldsymbol{\varepsilon} \)

sample

Product of two Gaussians is a Gaussian

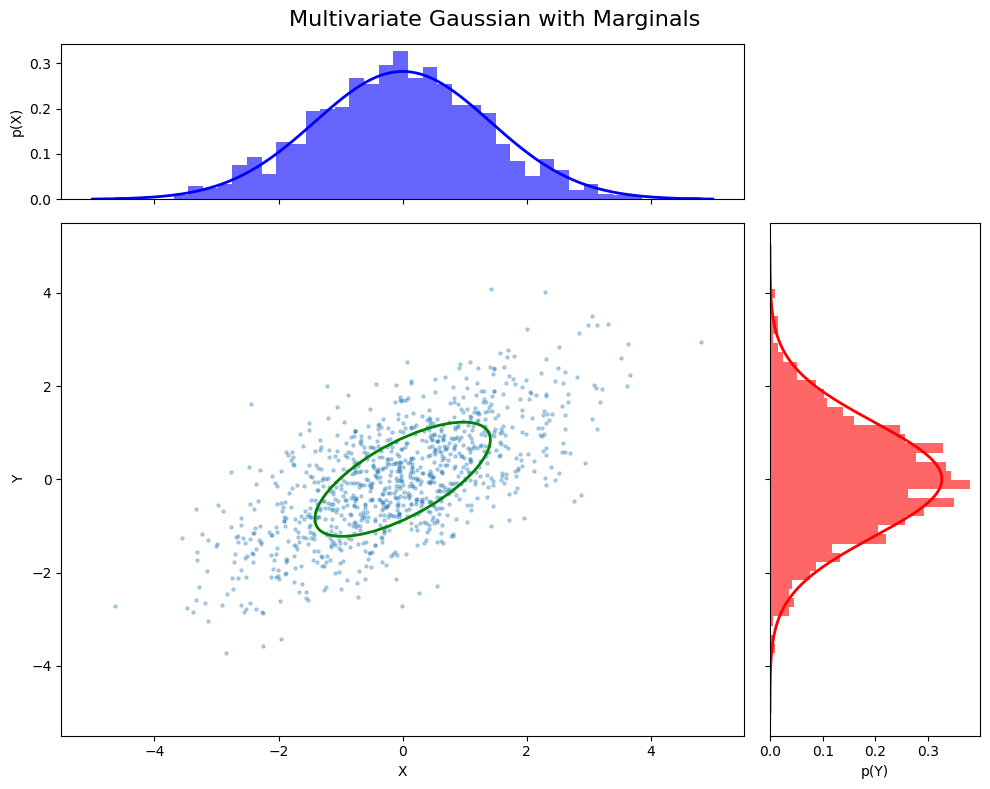
Multivariate Probability Distribution

A multivariate distribution models the joint behavior of multiple random variables simultaneously. For example, a Multivariate Gaussian models the probability of a vector \( \mathbf{x} = [x_1, x_2, …, x_n] \).

General Form:

\( p(\mathbf{x}) = p(x_1, x_2, \ldots, x_n) \)

Joint probability tells us the likelihood of all variables taking specific values together.

Multivariate Gaussian

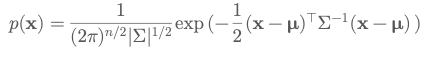
Conditional Probability:

Conditional probability quantifies the probability of an event given that another event has occurred.

Reads as: “The probability of x given y”.

Marginalization:

Marginalization is the process of finding the distribution of a subset of variables by summing or integrating out others.

Given \( p(x, y)\), the marginal of \(x\) is:

Interpretation: What is the probability of \( x \), regardless of \(y\)?

Bayes Rule:

Bayes’ Theorem relates conditional probabilities in both directions

Prior

Evidence

Likelihood

Posterior

Expected Value:

The expected value (mean) of a random variable is its long-run average outcome

Represents the “center” of a distribution.

Useful for predictions, variance calculation, and loss expectations.

But, what about images?

Where does your sample come from?

But, what about images?

Where does your sample come from?

unknown

Where does your sample come from?

unknown

But, what about images?

Images are multidimensional vectors

but, what does it mean when two images are closer to each other?

but, what does it mean when two images are closer to each other?

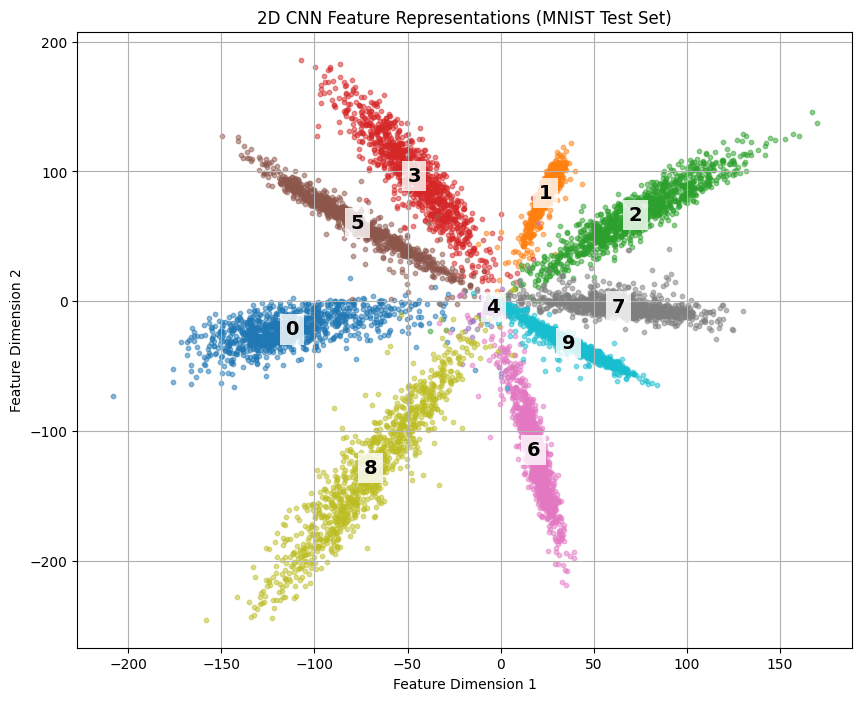
Let's do a small experiment...

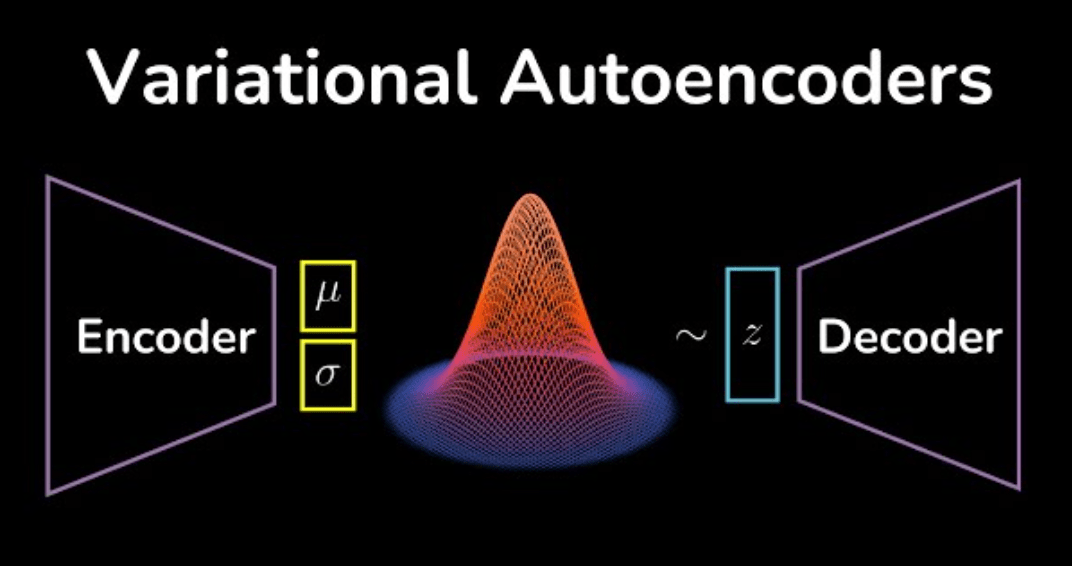
\( \mu \) and \( \sigma\) can be multi -dimensional

Data reconstruction using VAEs

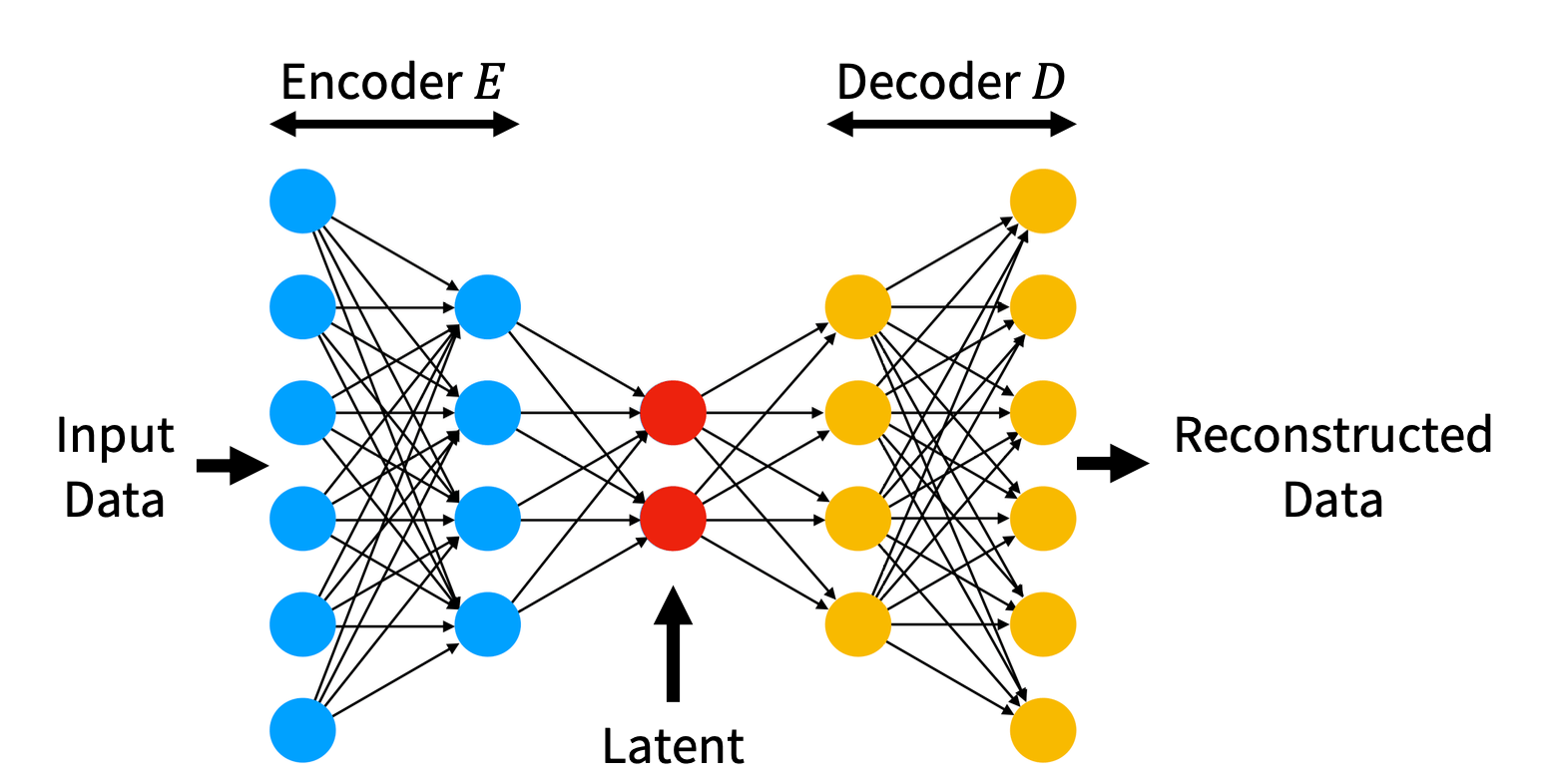
Posterior

Generative Model

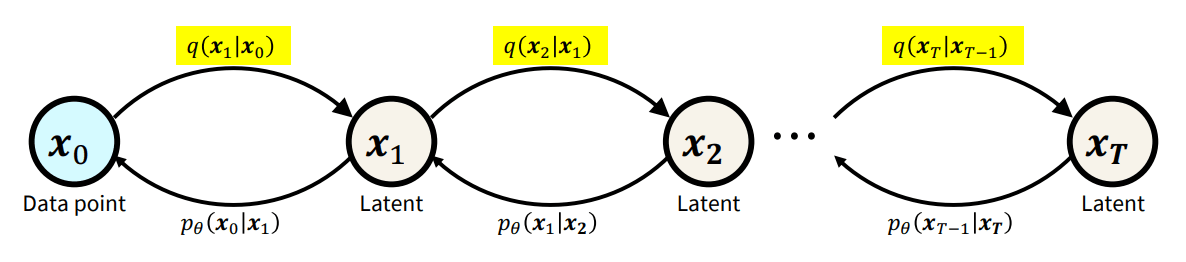
• Forward Process
• Reverse Process

Diffusion Models

• Forward Process
• Reverse Process

Diffusion Models

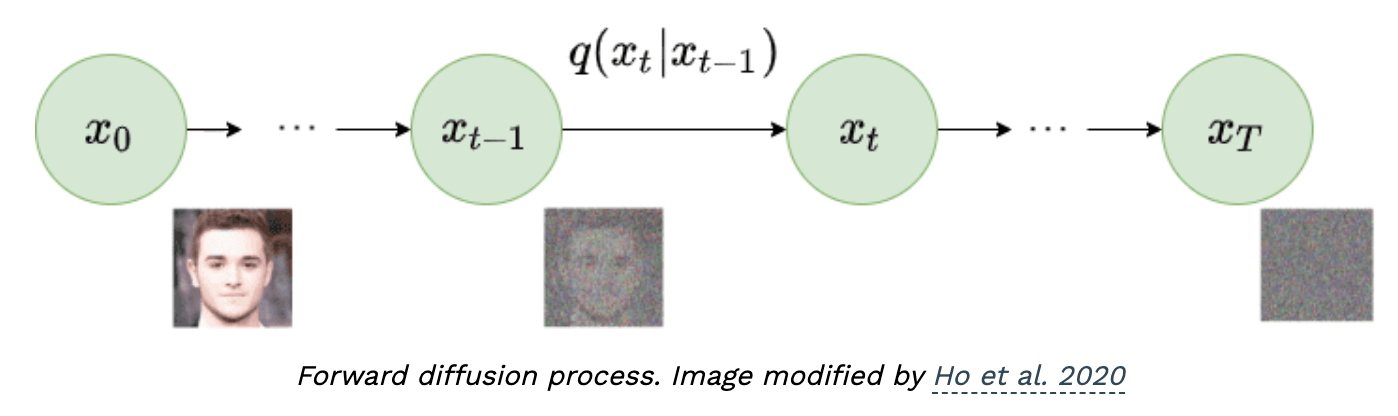
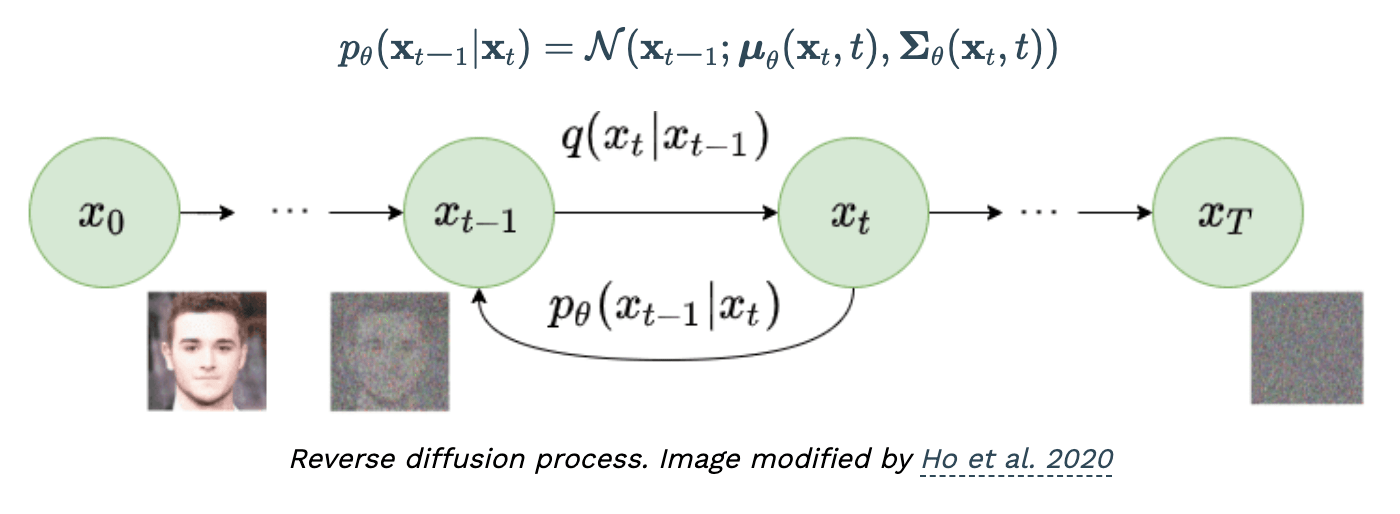
Let's discuss how to learn to denoise in the next lecture!!