Applications of Artificial Intelligence to Computational Chemistry
Nicholas J. Browning
Supervisor: Prof. Dr. Ursula Roethlisberger
- Introduction
- Motivation
- EVOLVE
- GAML
- ML-MTS
Overview
1
Science, 2018, 361, 6400, pp. 360-365
Chemical Design
2
Chemical Space
Space defined by all possible molecules given a set of construction rules and boundary conditions
Chemical spaces are vast
J. Am. Chem. Soc., 2009, 131, 25, pp 8732–8733
ACS Chem Neurosci., 2012, 3, 9, pp 649–657.
3
> 10^{60}
Chemical Accuracy
Full CI
HF
DFT
MP2
Computational Cost
Accuracy
CC
\text{Experiment}
\infin
4
Motivating Remarks
Designing new compounds with interesting properties requires searching incomprehensibly large chemical spaces
Requiring chemical accuracy for predicted properties engenders the use of computationally expensive electronic structure methods
5
1. Searching Chemical Space
2. Improving Chemical Accuracy, for Less
Evolutionary Algorithms
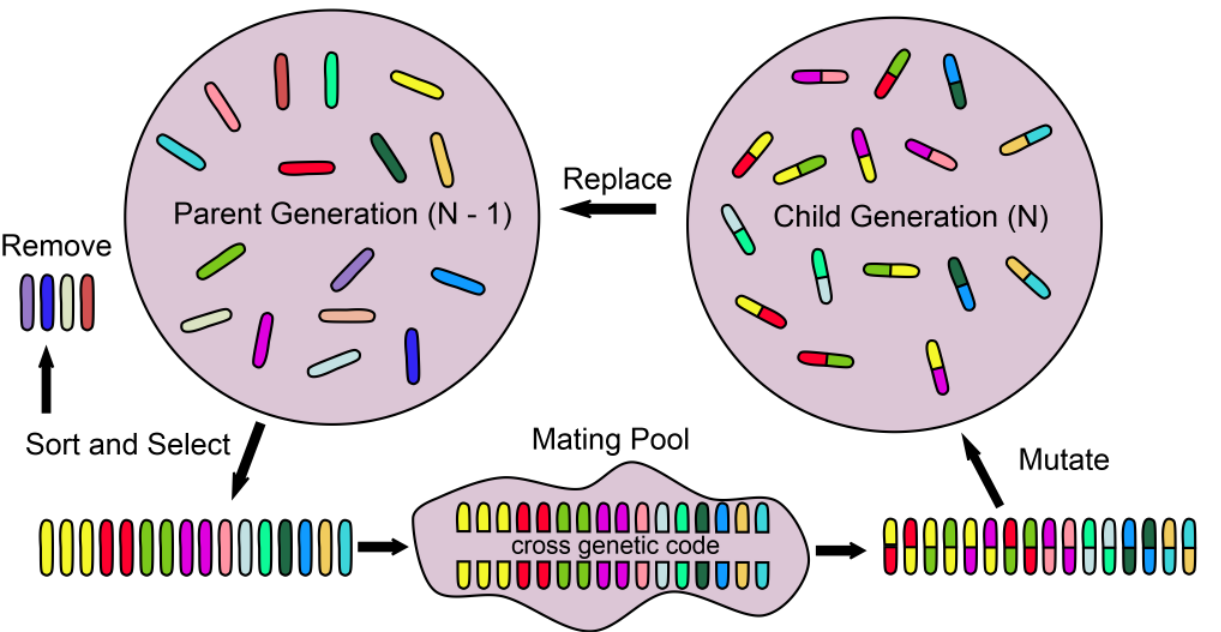
Optimisation algorithms inspired by biological processes or species behaviour
6
Particle Swarm Optimisation
Genetic Algorithms
Machine Learning
Replace expensive electronic structure calculation with cheaper, data-driven regression model
\left < \Psi| \hat H | \Psi \right >\rightarrow f(\{Z, R\})
7
Motivating Remarks
8
1. Searching Chemical Space
2. Improving Chemical Accuracy, for Less
EVOLVE: An Evolutionary Toolbox for the Design of Peptides and Proteins
Nicholas J. Browning, Marta A. S. Perez, Elizabeth Brunk, Ursula Roethlisberger, in submission, JCTC, 2019.
- Introduction
- Motivation
- EVOLVE
- GAML
- ML-MTS
Haemoglobin (PDB 1A3N)
- DNA Signalling
- Acid-base catalysis
- atom/group transfer
- Electron transfer
- Redox catalysis
Design of proteins is attractive:
- Tune or change activity
- Improve solvent tolerance
- Increase thermal stability
Proteins fulfill a wide scope of biological functions ranging from regulation to catalytic activity:
Protein Design
Issues:
- Search space is large
- E.g 50-residue protein:
20^{50} \approx 1 \times 10^{65}
possible sequences
9
Short 20-mer polyalanine
Central 8 residues open to mutation (purple spheres)
EVOLVE Algorithm and Prototype
Side chain dihedrals discretised into set of 177 low-energy conformers [1]
1. Proteins, 2000, 40, pp 389-408
10
\vec{\chi} = \{\chi_i\}
f = \Delta E^\text{mutant}_{\text{system}} - \Delta E^{\text{ref}}_\text{system} = E^\text{mutant}_\text{system} - E^\text{ref}_\text{system} + \sum_i^N (E^{\text{ref}}_\text{aa}(i) - E^{\text{mutant}}_\text{aa}(i))
E_\text{system} = E^{FF99SB}_\text{system} + \Delta G^{GB}_{sol}
Amber FF99SB force field
Solvent effects modelled by implicit solvent model
Backbone stability measure
\epsilon = 80
\epsilon = 5
0
\epsilon = 10
Buried Protein Environment
Solvent Exposed
Intermediary
EVOLVE Fitness Function
11
94 Rotamers
177 Rotamers
177 Rotamers
-40.6 kcal/mol
-28.4 kcal/mol
-42.3 kcal/mol
EVOLVE Optimisation Curves
12
Fittest Individuals - Hydrophobic Environment
94 Rotamers
f = -28.4 kcal/mol
Buried Core Protein
13
Solvent Exposed Environment
Fittest Individuals - Solvent Exposed Environment
14
177 Rotamers
f = -40.6 kcal/mol
Homohelix Study
-40.6 kcal/mol
-28.4 kcal/mol
-42.3 kcal/mol
-28.1 kcal/mol
-28.0 kcal/mol
-27.9 kcal/mol
W04
15
Selection probabilities show consistent convergence towards a subset of chemical space
Selection Probabilities
16
Can use this subset to focus GA exploration on more interesting regions
55 Rotamer subset of residues: TRP, GLU, ASP, HIP, ARG
New fitness: -42.4 kcal/mol
Subspace Search
17
Outlook
J. Am. Chem. Soc., 2018, 140, 13, pp 4517–4521
Mutant protein solvent and pH tolerant
Thermostability greatly increased compared to wild-type
B1 Domain Protein G
18
1. Searching Chemical Space
2. Improving Chemical Accuracy, for Less
Genetic Optimisation of Training Sets for Improved Machine Learning Models of Molecular Properties
Nicholas J. Browning, Raghu Ramakrishnan, O. Anatole von Lilienfeld, Ursula Roethlisberger, JPCL, 2017
- Introduction
- Motivation
- EVOLVE
- GAML
- ML-MTS
-
Can the error be improved by intelligent sampling - is less more?
-
Are there systematic trends in “optimal” training sets?
Chemical Interpolation
19
Chemical Database
8 heavy-atom subset of the QM-9 database [2]
10 thermochemical and electronic properties computed with DFT/B3LYP
2. Sci. Data, 2014, 1.
Out-of-sample test error used as fitness metric
Complex optimisation problem:
Database QM-8
Kernel Ridge Regression
\approx 10^{1449}
C(10900, 1000)
20
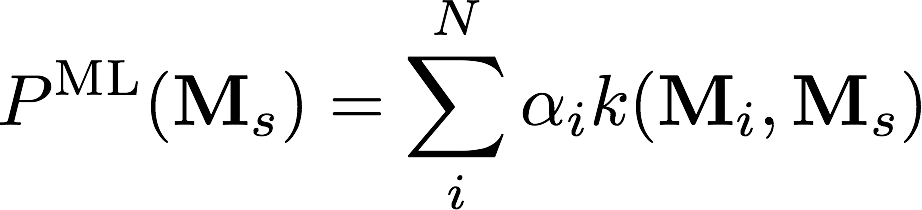
Significant reduction in out-of-sample errors
Fewer training molecules required to reach given accuracy
random sampling
GA optimised
Learning Curves - Enthalpy of Atomisation
21
Direct Learning
Delta Learning
Systematic Trends - Moments of Inertia
22
Certain molecules are more representative
Systematic shifts in distance, property, and shape distributions
Systematic Trends - Property Distributions
23
Certain molecules are more representative
Systematic shifts in distance, property, and shape distributions
Motivating Remarks
1. Searching Chemical Space
2. Improving Chemical Accuracy, for Less
24
Machine Learning Enhanced Multiple Time Step Ab Initio Molecular Dynamics
Nicholas J. Browning, Pablo Baudin, Elisa Liberatore, Ursula Roethlisberger
- Introduction
- Motivation
- EVOLVE
- GAML
- ML-MTS
Molecular Dynamics
Provides a 'window' into the microscopic motion of atoms in a system
F_A = -\nabla_A E_0(\{R, r\})
Forces acting on (classical) nuclei calculated from a potential energy surface
25
Key Issues
- the accuracy of the potential energy surface : ML
- timestep used to integrate atomic forces : MTS
Multiple Time Step Integrators
Address the time step issue by observing that the forces acting on a system have different timescales
Separate "fast" and "slow" components of the total force, which can be integrated using smaller and larger timesteps
Slow forces typically expensive to compute therefore MTS yields a computational gain
26
MTS Algorithm
\gamma = (q_1, q_2, \dots, q_N, p_1, p_2, \dots, p_N)
iL = iL_\text{fast} + iL_\text{slow}
a(\gamma_t) = e^{iLt}a(\gamma_0)
e^{iL\Delta t} \approx e^{iL_{slow} \frac{\Delta t}{2}} \times e^{iL_\text{fast}\Delta t} (\Delta t) \times e^{iL_{slow} \frac{\Delta t}{2}}
e^{iL\Delta t} \approx e^{iL^\text{slow} (\Delta t/2)} \Big[ e^{iL^\text{fast} (\Delta t/n)} \Big]^n e^{iL^\text{slow} (\Delta t/2)}
Propagatation of phase space vector
Separate slow and fast components
phase space vector
Discrete time propagator obtained from Trotter factorisation
# initialise x, p
dt = 0.36
Dt = dt*n
Fslow = compute_slow_forces(x)
Ffast = compute_fast_forces(x)
for t in range(0, total_time, Dt):
p = p + 0.5*Dt*Fslow # Integrate slow components
for i in range(1, n): # Integrate fast components
p = p + 0.5*dt*Ffast
x = x + dt * p/m
Ffast = compute_fast_forces(x)
p = p + 0.5*dt*Ffast
Fslow = compute_slow_forces(x)
p = p + 0.5*Dt*Fslow # Integrate slow components
27
\delta t
Ab Initio MTS
28
Machine Learning Potentials
Replace expensive electronic structure method with data-driven kernel model
Delta-learning model naturally results in an MTS scheme
F^\text{fast} = F^\text{low}
F^\text{slow} = \Delta F^\text{ML}
F^\text{fast} = F^\text{low} + \Delta F^\text{ML}
F^\text{slow} = F^\text{high} - F^\text{fast}
Scheme I ML-MTS
Scheme II ML-MTS
\Delta F^\text{ML} = F^\text{high} - F^\text{low}
Exact slow forces
Cost of high level, evaluated infrequently
Approximate slow forces
Cost of low level
29
\Delta E^\text{ML}(M_I) = E^\text{high}(M_I) - E^\text{low}(M_I) = \sum_I\sum_J k(M_I, M_J) \alpha_J
\Delta F_L^\text{ML}(M_I) = -\frac{\partial \Delta E^\text{ML}}{\partial R_L}(M_I) = -\sum_I\sum_J \frac{\partial k(M_I, M_J)}{\partial M_I} \frac{\partial M_I}{\partial R_L} \alpha_J
Use a computationally efficient kernel method [3]:
- Generalisable
- No 2nd derivatives required, only kernel and descriptor gradients
Representation:
-
Atomic environments: Atomic Spectrum of London-Axilrod-Teller-Muto representation (aSLATM) [4]
MPI-ML code implemented into CPMD
Machine Learning Potentials
3. Chem. Phys., 2019, 150, 064105
4. ArXiv, 2017, https://arxiv.org/abs/1707.04146
30
Training Data
Trajectories of small isolated N-water molecule clusters
Fast components = LDA
Slow components = PBE0 - LDA
Predictions made on liquid water
31
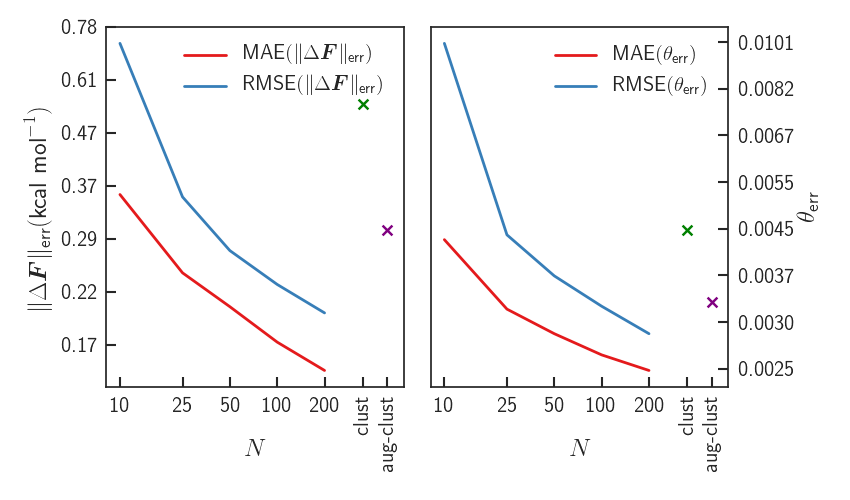
Results - Errors
32
Results - Errors
Significant improvement upon LDA - forces almost identical to PBE0
33
Results - Time Step and Speedup
Significant increase in outer timestep wrt. standard MTS
Resonance effects limit maximum outer timestep
Encouraging increase in overall speedup
Speedup dictated by number of SCF cycles to converge wfn
\epsilon = \frac{1}{N}\sum_i \frac{E_i - \bar{E}}{\bar E}
34
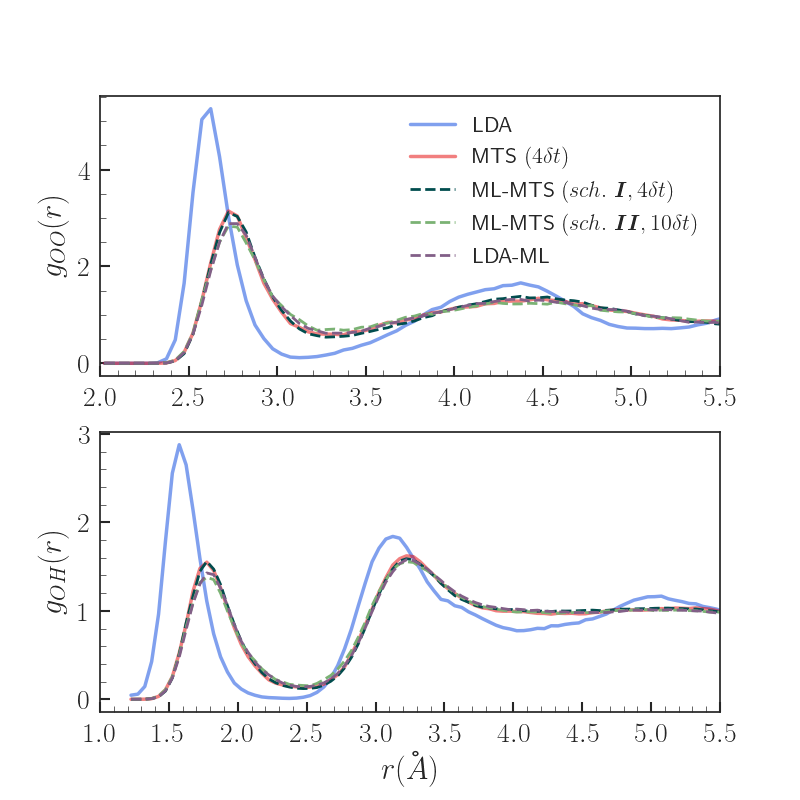
Results - Properties
MTS (n=4dt) identified as yielding properties with excellent agreement wrt. VV-PBE0 in previous work [5]
Both scheme I and II ML-MTS result in significantly improved radial distributions
5. J. Chem. Theory Comput., 2018, 14, 6, pp 2834–2842
35
1. Searching Chemical Space
Conclusions
- EVOLVE is capable of searching through inordinately large chemical spaces
- Meaningful chemical space insights can be gained from the EVOLVE procedure
- Potential for experimental reach
36
2. Improving Chemical Accuracy, for Less
-
Within a specified chemical space, the accuracy of ML models can be significantly improved with intelligent sampling
-
kernel methods can provide a significant increase in timestep used in MTS integrators
- Maintain good accuracy
- Significantly reduce computational cost
Acknowledgements and Thanks
Dr. Raghu Ramakrishnan
Dr. Esra Bozkurt
Dr. Marta A. S. Perez
Dr. Pablo Baudin
Dr. Elisa Liberatore
Prof. Ursula Roethlisberger
37
Prof. O. Anatole von Lilienfeld
Prof. Clemence Corminboeuf
Dr. Albert Bartók-Pártay
Dr. Ruud Hovius
Acknowledgements and Thanks
38
Thermostability Measure
f = \Delta E^\text{mutant}_{\text{system}} - \Delta E^{\text{ref}}_\text{system} = E^\text{mutant}_\text{system} - E^\text{ref}_\text{system} + \sum_i^N (E^{\text{ref}}_\text{aa}(i) - E^{\text{mutant}}_\text{aa}(i))
E_\text{system} = E^{FF99SB}_\text{system} + \Delta G^{GB}_{OBC}
Backbone stability measure
M. A. S. Perez, E. Bozkurt, N. J. Browning U. Roethlisberger, in preparation
39
Thermostability Measure
40
Manual Mutations
\epsilon = 80
D03-E05 -> R*-E05... = -30.1 kcal/mol
-40.6 kcal/mol
-28.4 kcal/mol
-42.3 kcal/mol
D03-E05 -> E*-E05... = -39.2 kcal/mol
\epsilon = 10
W04-W04-W04-W04-F04-Q05-W04 -> {8 x W*} = -28.2 kcal/mol
41
EVOLVE: MOGA
42
Amino Acids
43
GA-ML Small Optimal Training Sets
44
GA-ML Distance Distributions
45
\boldsymbol{M}_I^{(2)}(r) = \frac{1}{2} \sum_{J\ne I} Z_IZ_J \frac{1}{\sigma_r \sqrt{2\pi} r^6} e^{-\frac{\left \lVert r - R_{IJ} \right \rVert ^2}{2\sigma_r^2}}
\boldsymbol{M}_I^{(3)}(\theta)= \frac{1}{3}\sum_{I \ne J \ne K} Z_I Z_J Z_K \frac{1}{\sigma_\theta \sqrt{2\pi}} e^{-\frac{\left ( \theta - \theta_{IJK} \right )^2}{2\sigma_\theta^2}} \frac{1 + \cos\theta \cos\theta_{JKI}\cos\theta_{KIJ}}{\left (R_{IJ} R_{IK} R_{KJ}\right)^3}
\boldsymbol{M}_I = \left \{ \boldsymbol{M}^{(1)}_I, \boldsymbol{M}^{(2)}_I, \boldsymbol{M}^{(3)}_I\right \}
SLATM Parameters
46
R_c = 4.8 A
\theta_\text{min} = -0.35 \ \text{rad}
\theta_\text{max} = 3.5 \ \text{rad}
\text{grid resolution}= 0.1A
\text{angular grid resolution}= 0.1
\ \text{rad}
Two-body term:
Three-body term:
\sigma_r = 0.05
\sigma_{\theta} = 0.05
Thermostability
47
Applications of Artificial Intelligence to Computational Chemistry
By Nick Browning
