EVOLVE

Particle Swarms for optimisation

Nicholas Browning

A Multi-objective Evolutionary Toolbox

Introduction

  • Swarm Intelligence
  • Applications
  • Introduction to Particle Swarm Optimization (PSO)
    • The Idea
    • The Implementation (Vanilla)
    • Topology
  • PSO Variants
    • Constriction PSO (CPSO)
    • Fully informed PSO (FIPSO)
  • Benchmark Functions
  • Benchmark Analysis
  • Cool Videos

Swarm Intelligence

Swarm Intelligence

Swarm Intelligence

Artificial intelligence technique based on study of collective behaviour in decentralised, self-organised systems.

 

Population of simple "agents" capable of interacting locally, and with their enviroment.

 

Usually no centre of control - local interactions between agents usually leads to global behaviour

Swarm Intelligence

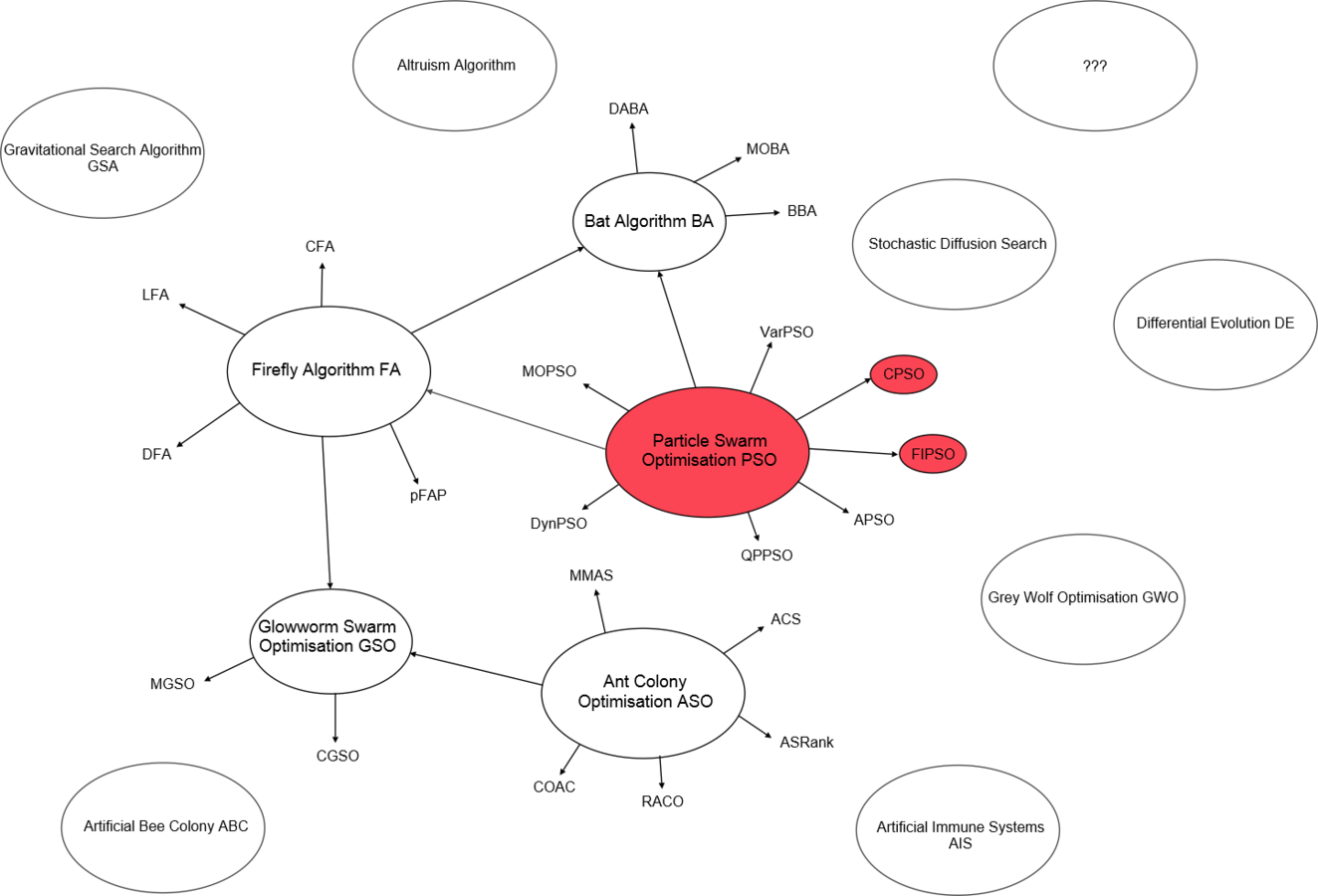
Swarm Intelligence

Sunderland A.F.C PSO?

Swarm Intelligence

5 tenets of swarm intelligence, proposed by Millonas [1]

  • Proximity:  simple space and time calculations
  • Quality: respond to quality factors in the environment
  • Diverse Response: activites must not occur along excessively narrow channels
  • Stability: mode of behaviour should not change upon environment change.
  • Adaptability: Mode of behaviour must be able to change if it's "worth" the computational price
[1] M. M. Milonas. Swarms, Phase Transitions, and Collective Intelligence. Artificial Life III, Addison Wesley, Reading, MA, 1994.

Applications

Also Batman, LOTR, Lion king, Happy Feet...

Particle Swarm Optimisation

First proposed by J. Kennedy and R. Eberhart [2], intent to imitate social behaviour of animals which display herding/swarming characteristics.
 

Each individual in the swarm learns from both its own past experiences (cognitive behaviour) and also from its surrounding neighbours (social behaviour).

 

Optimisation was not intentional!

[2] Kennedy, J.; Eberhart R., Particle Swarm Optimisation, Proc. Int. Conf. Neural Networks, 1995.
\vec{X}_i = \vec{X}_{min} + \vec{U}[0, 1] \odot (\vec{X}_{max} - \vec{X}_{min})
​X​⃗​​​i​​=​X​⃗​​​min​​+​U​⃗​​[0,1]⊙(​X​⃗​​​max​​−​X​⃗​​​min​​)
\vec{V}_i^t = (-\vec{X}_{min} + \vec{U}[0, 2] \odot (\vec{X}_{max} - \vec{X}_{min}))
​V​⃗​​​i​t​​=(−​X​⃗​​​min​​+​U​⃗​​[0,2]⊙(​X​⃗​​​max​​−​X​⃗​​​min​​))

Each particle is initialized in space: 

Each particle must move and hence has a velocity:

The Implementation (Vanilla)

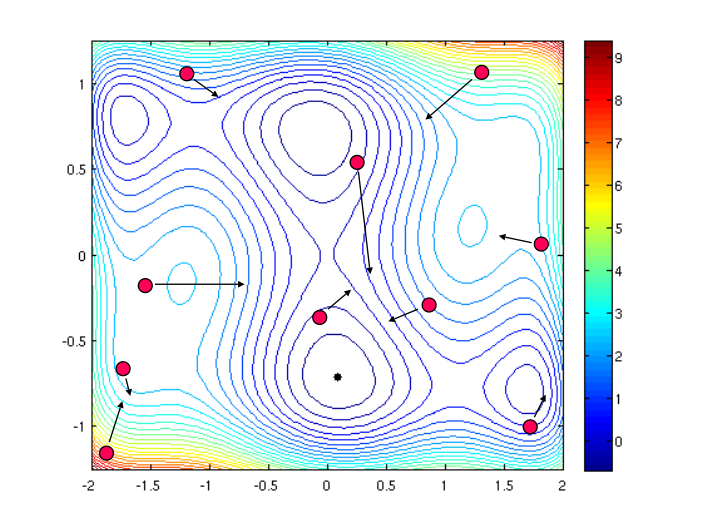
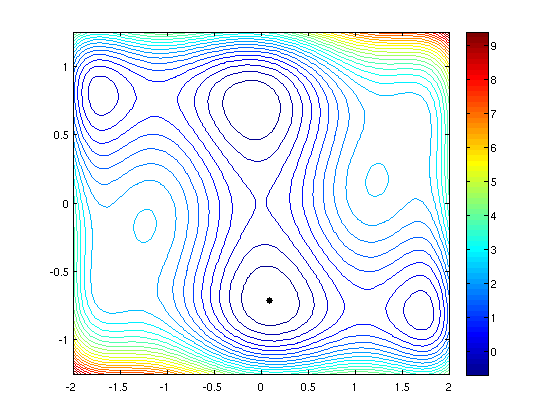
The Implementation (Vanilla)

How is cognitive and social learning achieved?

COGNITIVE AND SOCIAL INFLUENCE

\vec{V}_i^{t+1} = w\vec{V}_i^t + \vec{U}[0, c_l]\odot(\vec{P}_i - \vec{X}_i^t) + \vec{U}[0, c_g] \odot (\vec{P}_g - \vec{X}_i^t)
V⃗it+1=wV⃗it+U⃗[0,cl]⊙(P⃗i−X⃗it)+U⃗[0,cg]⊙(P⃗g−X⃗it)\vec{V}_i^{t+1} = w\vec{V}_i^t + \vec{U}[0, c_l]\odot(\vec{P}_i - \vec{X}_i^t) + \vec{U}[0, c_g] \odot (\vec{P}_g - \vec{X}_i^t)
\vec{X}_i^{t+1} = \vec{X}_i^t + \vec{V}_i^{t+1}\Delta t
X⃗it+1=X⃗it+V⃗it+1Δt\vec{X}_i^{t+1} = \vec{X}_i^t + \vec{V}_i^{t+1}\Delta t

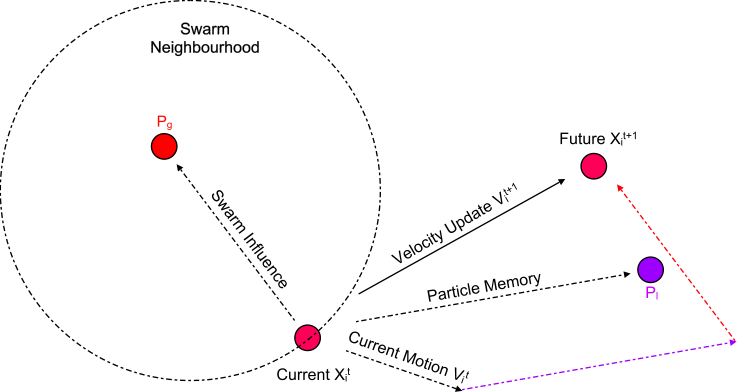
The Implementation (Vanilla)

Velocity update is defined by: 

New particle position can then be calculated: 

Cognitive Influence

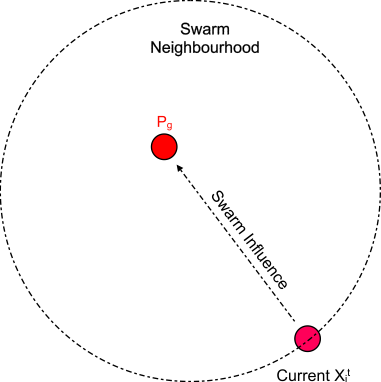
Swarm Influence

\vec{P}_m = \frac{(\vec{U}[0, c_l] \odot P_i +\vec{U}[0, c_g] \odot P_g)} {\vec{U}[0, c_l] + \vec{U}[0, c_g] }
P⃗m=(U⃗[0,cl]⊙Pi+U⃗[0,cg]⊙Pg)U⃗[0,cl]+U⃗[0,cg]\vec{P}_m = \frac{(\vec{U}[0, c_l] \odot P_i +\vec{U}[0, c_g] \odot P_g)} {\vec{U}[0, c_l] + \vec{U}[0, c_g] }

Particle will cycle unevenly about the point:

SWARM NEIGHBOURHOOD: TOPOLOGY

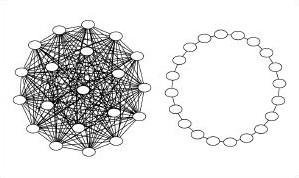
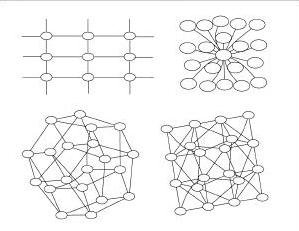
All

Ring

2D Von Neumann

3D Von Neumann

Star

Pyramid

Many graph representations possible!

Clerc [3] adapted PSO algorithm to include constriction coefficient. Convergence guaranteed, but not necessarily to global optimum.

Eberhart and Shi [4] later proposed modified version with improved performance

\vec{V}_i^{t+1} = K[\vec{V}_i^t + \vec{U}[0, c_l]\odot (\vec{P}_i^l - \vec{X}_i^t) + \vec{U}[0,c_g]\odot(\vec{P}_g - \vec{X}_i^t)]
V⃗it+1=K[V⃗it+U⃗[0,cl]⊙(P⃗il−X⃗it)+U⃗[0,cg]⊙(P⃗g−X⃗it)]\vec{V}_i^{t+1} = K[\vec{V}_i^t + \vec{U}[0, c_l]\odot (\vec{P}_i^l - \vec{X}_i^t) + \vec{U}[0,c_g]\odot(\vec{P}_g - \vec{X}_i^t)]

Constriction PSO

[3] M. Clerc. The Swarm and the Queen: Towards a Deterministic and Adaptive Particle Swarm Optimisation, Evolutionary Computation, 1999.
[4] R. C. Eberhart, Y. Shi. Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimisation, Evolutionary Computation, 2000.
K = \frac {2} {|2 - \psi - \sqrt{\psi^2 -4\psi}}
K=2∣2−ψ−ψ2−4ψK = \frac {2} {|2 - \psi - \sqrt{\psi^2 -4\psi}}
\psi = c_l + c_g; \psi > 4
ψ=cl+cg;ψ>4\psi = c_l + c_g; \psi > 4

Particle searches through it's neighbours to identify the one with the best result: biases the search in a promising direction

Fully informed PSO

Perhaps chosen neighbour is in fact not in a better region, and is simply heading toward a local optima?

Important information may be neglected through overemphasis on a single best neighbour

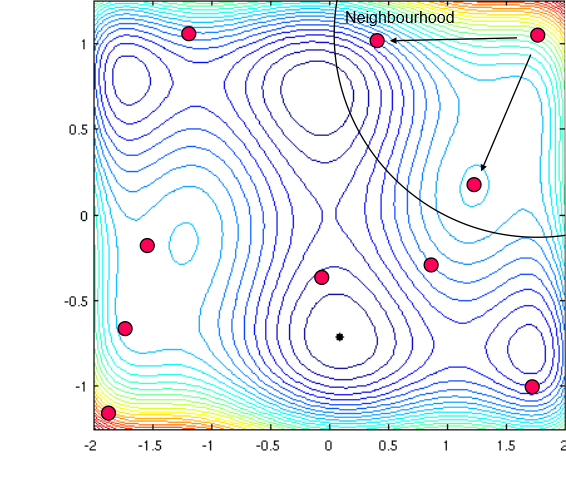
Fully informed PSO

\vec{V_i^{t+1}} = K[\vec{V}_i^t + \frac{1}{N_i}\sum_{j=1}^{N_i}U(0, \psi) \odot (\vec{P}_j - \vec{X}_i^t)]
Vit+1⃗=K[V⃗it+1Ni∑j=1NiU(0,ψ)⊙(P⃗j−X⃗it)]\vec{V_i^{t+1}} = K[\vec{V}_i^t + \frac{1}{N_i}\sum_{j=1}^{N_i}U(0, \psi) \odot (\vec{P}_j - \vec{X}_i^t)]
\psi > 4
ψ>4\psi > 4
K = \frac {2} {|2 - \psi - \sqrt{\psi^2 -4\psi}}
K=2∣2−ψ−ψ2−4ψK = \frac {2} {|2 - \psi - \sqrt{\psi^2 -4\psi}}

Mendes et al. [5] proposed a PSO variant which captures a weighted average influence of all particles in neighbourhood. Poli et al. [6] proposed the following simplified FIPSO update equation:

[5] R. Mendes, J. Kennedy, and J. Neves. The Fully Informed Particle Swarm: Simpler, Maybe Better. IEEE Transactions on Evolutionary Computation, 2004.
[6] R. Poli, J. Kennedy and T. Blackwell. Particle Swarm Optimisation: An Overview. Swarm Intell., 2007.

Benchmark functions

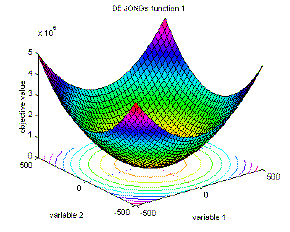
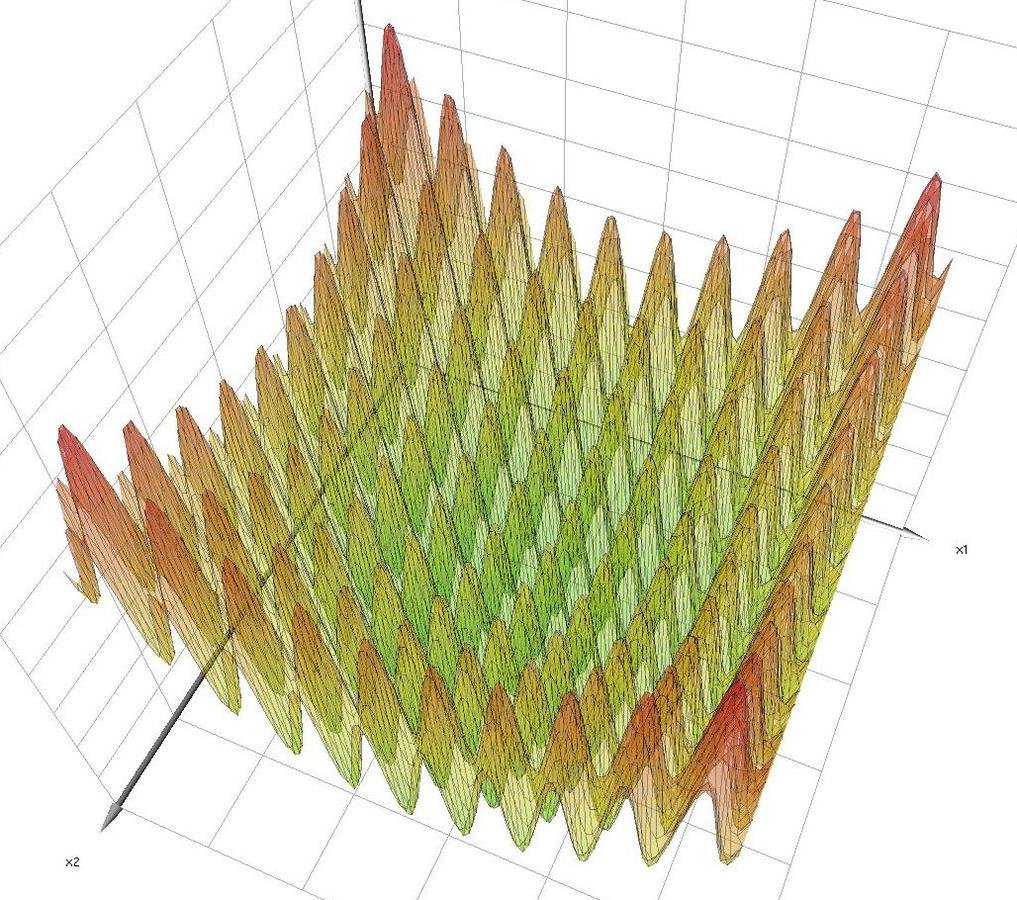
De Jong's Standard Sphere Function

Eggcrate Function

h(\vec x) = \sum_{i=1}^{d} x_i^2
h(x⃗)=∑i=1dxi2h(\vec x) = \sum_{i=1}^{d} x_i^2
g(x, y) = x^2 + y^2 + 25(\sin^2(x) + \sin^2(y))
g(x,y)=x2+y2+25(sin2(x)+sin2(y))g(x, y) = x^2 + y^2 + 25(\sin^2(x) + \sin^2(y))
h_{min} (\vec x) = 0; \vec x = 0
hmin(x⃗)=0;x⃗=0h_{min} (\vec x) = 0; \vec x = 0
g_{min} (x, y) = 0; x,y = 0
gmin(x,y)=0;x,y=0g_{min} (x, y) = 0; x,y = 0

Benchmark functions

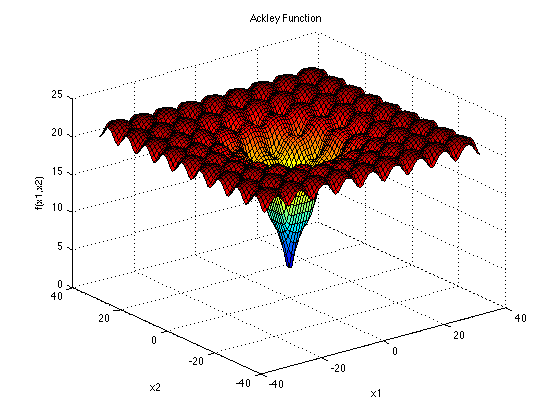
Ackley's Function

s(\vec{x}) = 20 + e -20\exp{[-0.2 \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_i^2}] - \exp{[\frac{1}{d}\sum_{i=1}^d cos(2 \pi x_i)}]}
s(x⃗)=20+e−20exp[−0.21d∑i=1dxi2]−exp[1d∑i=1dcos(2πxi)]s(\vec{x}) = 20 + e -20\exp{[-0.2 \sqrt{\frac{1}{d} \sum_{i=1}^{d} x_i^2}] - \exp{[\frac{1}{d}\sum_{i=1}^d cos(2 \pi x_i)}]}
s_{min} (\vec x) = 0; \vec x = 0
smin(x⃗)=0;x⃗=0s_{min} (\vec x) = 0; \vec x = 0
-30 \leq x_i \leq 30
−30≤xi≤30-30 \leq x_i \leq 30

Benchmark functions

Rosenbrock's Function

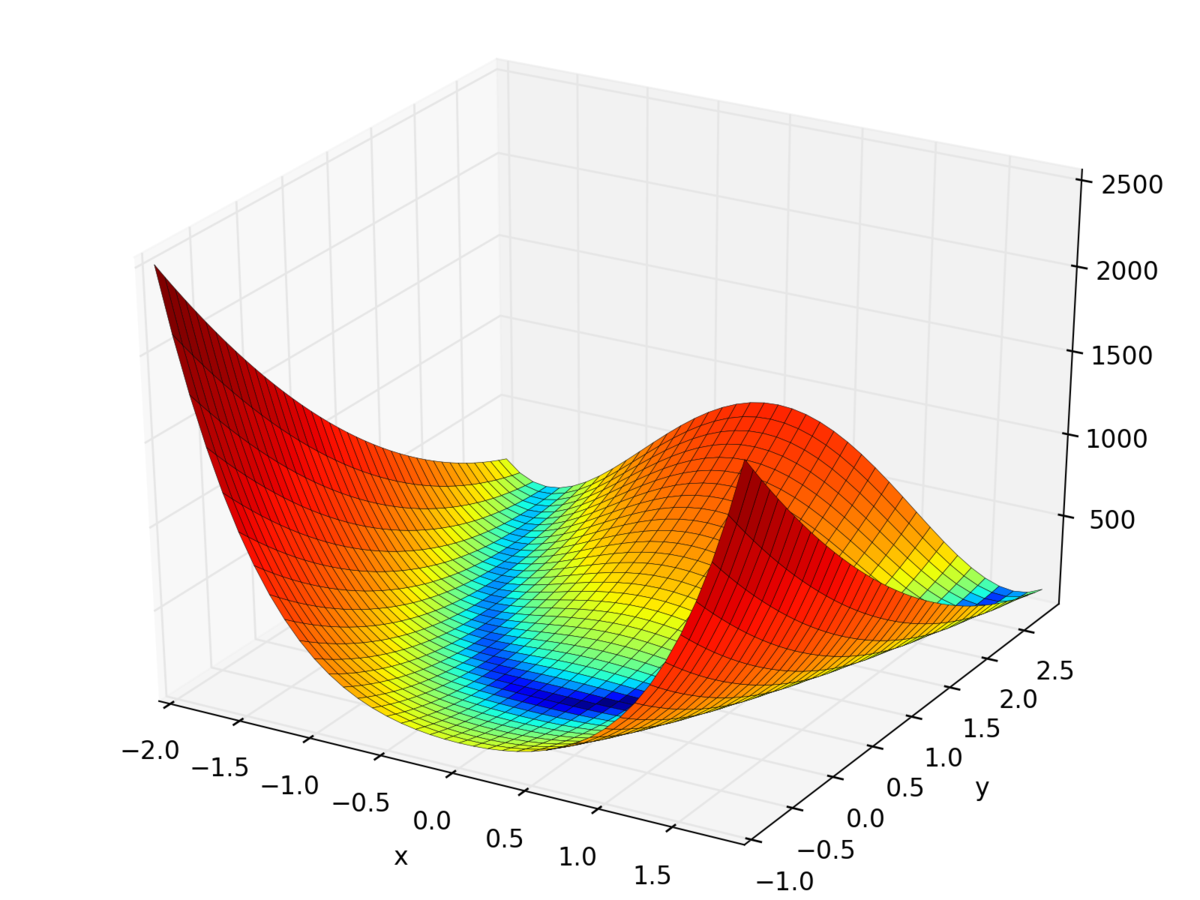
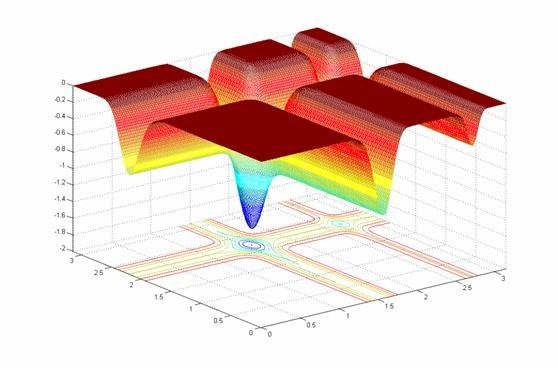
Michaelewicz's Function

f(\vec{x}) = - \sum _{i=1}^d sin(x_i)[sin(\frac{ix_i^2}{\pi})]^{2m}
f(x⃗)=−∑i=1dsin(xi)[sin(ixi2π)]2mf(\vec{x}) = - \sum _{i=1}^d sin(x_i)[sin(\frac{ix_i^2}{\pi})]^{2m}
f(\vec{x}) = \sum_{i=1}^{d-1} [(1-x_i)^2 + 100(x_{i+1} - x_i^2)^2]
f(x⃗)=∑i=1d−1[(1−xi)2+100(xi+1−xi2)2]f(\vec{x}) = \sum_{i=1}^{d-1} [(1-x_i)^2 + 100(x_{i+1} - x_i^2)^2]
-2048 \leq x_i \leq 2048
−2048≤xi≤2048-2048 \leq x_i \leq 2048
f_{min} (\vec x) = 0; \vec x = 0
fmin(x⃗)=0;x⃗=0f_{min} (\vec x) = 0; \vec x = 0

d! local minima in domain

0 \leq x_i \leq \pi
0≤xi≤π0 \leq x_i \leq \pi

where i = 1, 2, ..., d

f_{min} ^ {d=2} \approx -1.801
fmind=2≈−1.801f_{min} ^ {d=2} \approx -1.801
f_{min} ^ {d=5} \approx -4.6877
fmind=5≈−4.6877f_{min} ^ {d=5} \approx -4.6877

Benchmark functions

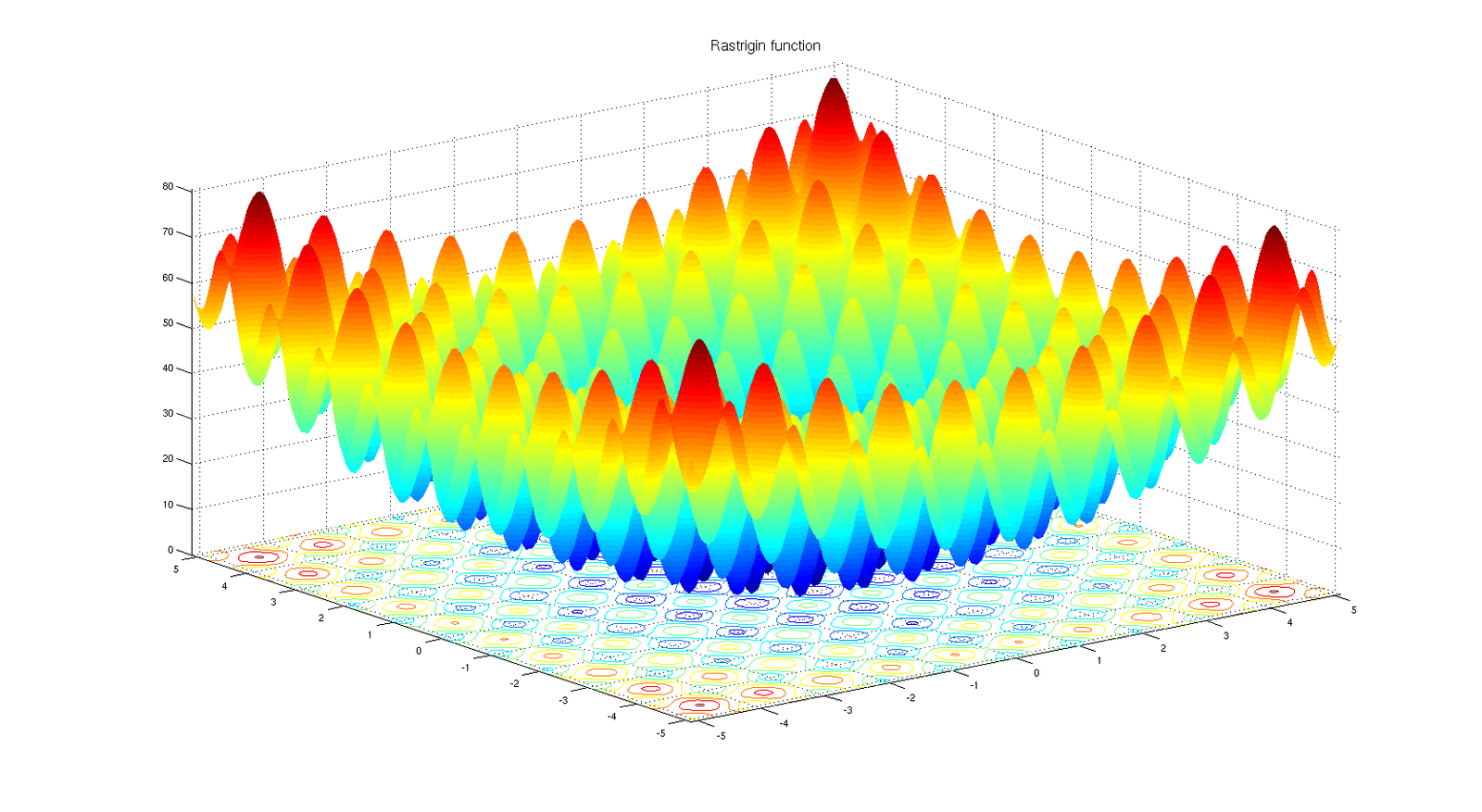
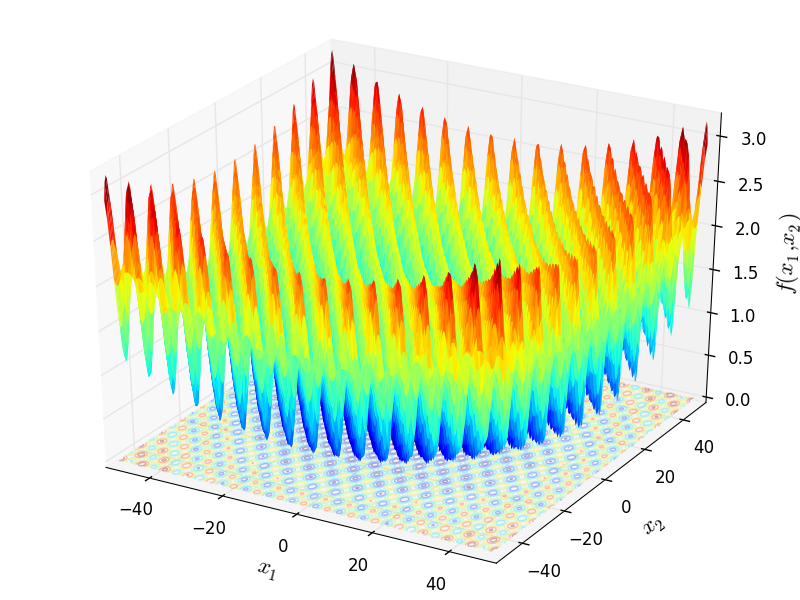
Rastrigrin's Function

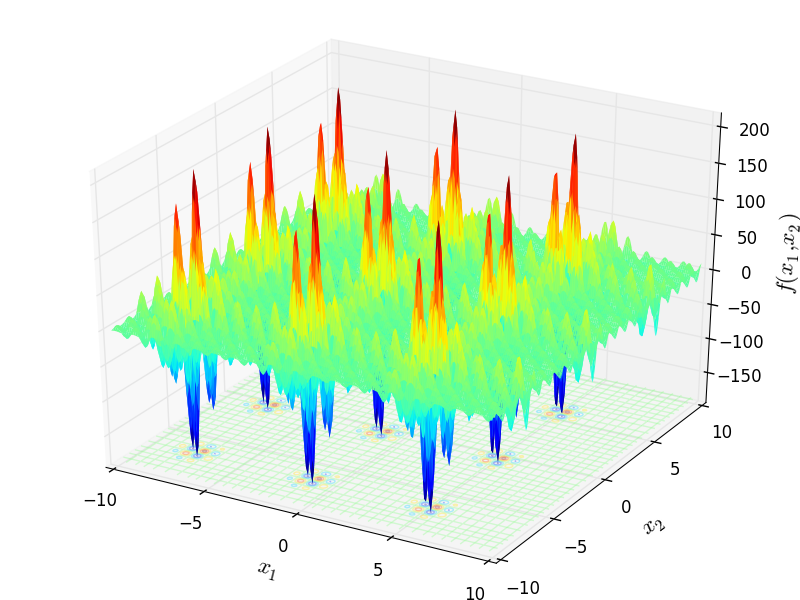
Griewank's Function

f (\vec{x}) = 1 + \frac{1}{4000} \sum_{i=1}^d x_i^2 - \prod_{i=1}^d\cos{\frac{x_i}{\sqrt{i}}}
f(x⃗)=1+14000∑i=1dxi2−∏i=1dcosxiif (\vec{x}) = 1 + \frac{1}{4000} \sum_{i=1}^d x_i^2 - \prod_{i=1}^d\cos{\frac{x_i}{\sqrt{i}}}
-600 \leq x_i \leq 600
−600≤xi≤600-600 \leq x_i \leq 600
f_{min} (\vec{x}) = 0; \vec x = 0
fmin(x⃗)=0;x⃗=0f_{min} (\vec{x}) = 0; \vec x = 0
f(\vec x) = Ad + \sum_{i=1}^d(x_i^2 - A\cos{2\pi x_i})
f(x⃗)=Ad+∑i=1d(xi2−Acos2πxi)f(\vec x) = Ad + \sum_{i=1}^d(x_i^2 - A\cos{2\pi x_i})
A = 10; x \in [-5.12, 5.12]
A=10;x∈[−5.12,5.12]A = 10; x \in [-5.12, 5.12]
f_{min}(\vec x) = 0 ; \vec x = 0
fmin(x⃗)=0;x⃗=0f_{min}(\vec x) = 0 ; \vec x = 0

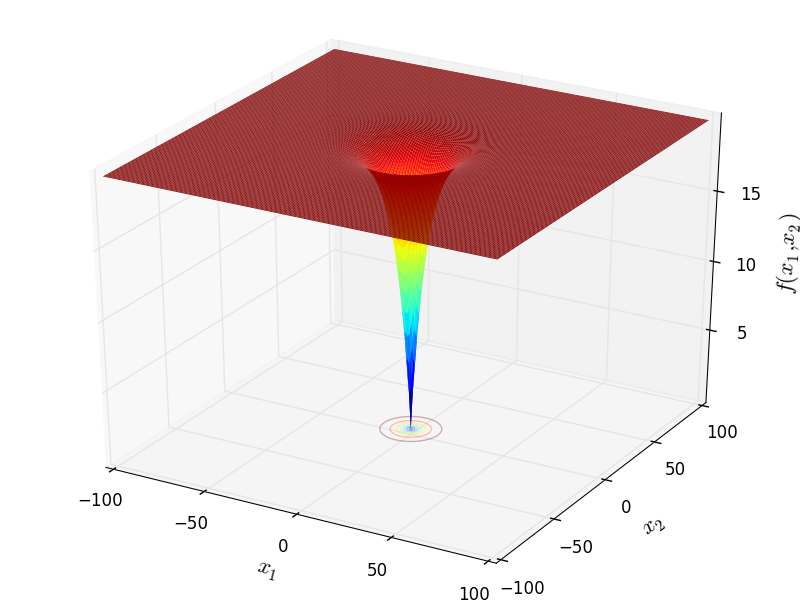
Benchmark functions

f(x, y) = -\cos{x}\cos{y}\exp{(-(x-\pi)^2-(y-\pi)^2})
f(x,y)=−cosxcosyexp(−(x−π)2−(y−π)2)f(x, y) = -\cos{x}\cos{y}\exp{(-(x-\pi)^2-(y-\pi)^2})

Easom's Function

f_{min}(x, y) = -1; (\pi, \pi)
fmin(x,y)=−1;(π,π)f_{min}(x, y) = -1; (\pi, \pi)
x,y \in [-100, 100]
x,y∈[−100,100]x,y \in [-100, 100]
f(x, y) = (\sum_{i=1}^5i\cos{(i+1)x + i})(\sum_{i=1}^5i\cos{(i+1)y + i})
f(x,y)=(∑i=15icos(i+1)x+i)(∑i=15icos(i+1)y+i)f(x, y) = (\sum_{i=1}^5i\cos{(i+1)x + i})(\sum_{i=1}^5i\cos{(i+1)y + i})

Shubert's Function

f_{min}(x, y) = -186.7309
fmin(x,y)=−186.7309f_{min}(x, y) = -186.7309
x,y \in [-10, 10]
x,y∈[−10,10]x,y \in [-10, 10]

Dynamics Visualisation

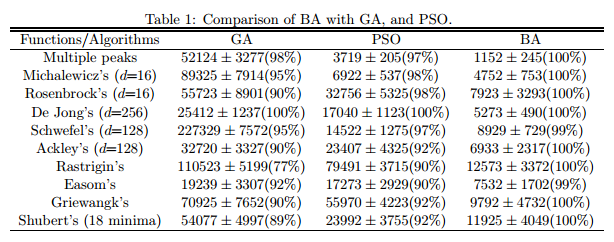
Benchmark Analysis

Comparison performed by Yang [7] - study introduces new PSO variant: "The Bat Algorithm"

[7] X. S. Yang. A New Metaheurstic Bat-Inspired Algorithm. Nature Inspired Cooperative Strategies for Optimisation, 2010.

Dynamic Optima

PSO in Theatre

Glowworm swarm Optimisation

Bat swarm algorithm

Special variant of PSO

Other similar ideas exist e.g Glowworm algorithm

 

based on the echolocation behaviour of microbats with varying pulse rates of emission and loudness.

TODO

EVOLVE - Particle Swarms for Optimisation

By Nick Browning

Made with Slides.com

EVOLVE - Particle Swarms for Optimisation

  • 934

More from Nick Browning

  • Public: Applications of Artificial Intelligence to Computational Chemistry
    Nick Browning
    637
  • Applications of Artificial Intelligence to Computational Chemistry
    Nick Browning
    653
  • Genetic Optimisation of Training Sets for Improved Machine Learning Models of Molecular Properties
    Nick Browning
    573