Fast simulation of Rigid Multibody Quasistatic Systems with Convex Optimization
Tao Pang and Russ Tedrake
Robot Locomotion Group
{pangtao, russt}@csail.mit.edu
Outline
- Simulation for robotic manipulation:
- Lots of contacts,
- Things move slowly.
- A fast time-stepping simulation scheme that combines
- Anitescu's Coulomb friction model,
- the simulation can be formulated as a convex quadratic program (QP).
- Simplifying assumptions for manipulation:
- The world is quasistatic,
- Robots are modeled as impedances.
- Anitescu's Coulomb friction model,
- Biggest advantage: use of larger (sometimes 100x) time steps than 2nd-order dynamics.
Simulating contacts
- Contact force/impulse and signed distance satisfy complementarity constraints:
0 \leq \lambda_n \perp \phi \geq 0
- Optimization problems that have complementarity constraints are generally non-convex.
- In the frictionless case, complementarity constraints emerge as the KKT conditions of a convex quadratic program (QP).
Normal contact force/impulse.
Signed distance.
\phi
\lambda_n
normal contact force
\min \frac{1}{2}k x^2 \\
\text{s.t.} x \geq r
KKT conditions
f = -kx
spring force
r
(x - r) \lambda = 0
complementary slackness
kx - \lambda = 0
zero gradient (force balance)
x \geq r, \lambda \geq 0
primal and dual feasibility
\iff
\lambda_n \geq 0 \\
\phi \geq 0 \\
\lambda \phi = 0
x
Simulating contacts
- But for frictional contacts, contact forces need to satisfy additional constraints:
- Friction cone,
- maximum dissipation principle.
- These additional constraints mean that contact forces need to be explicitly included in the optimization as decision variables, making the problem non-convex:
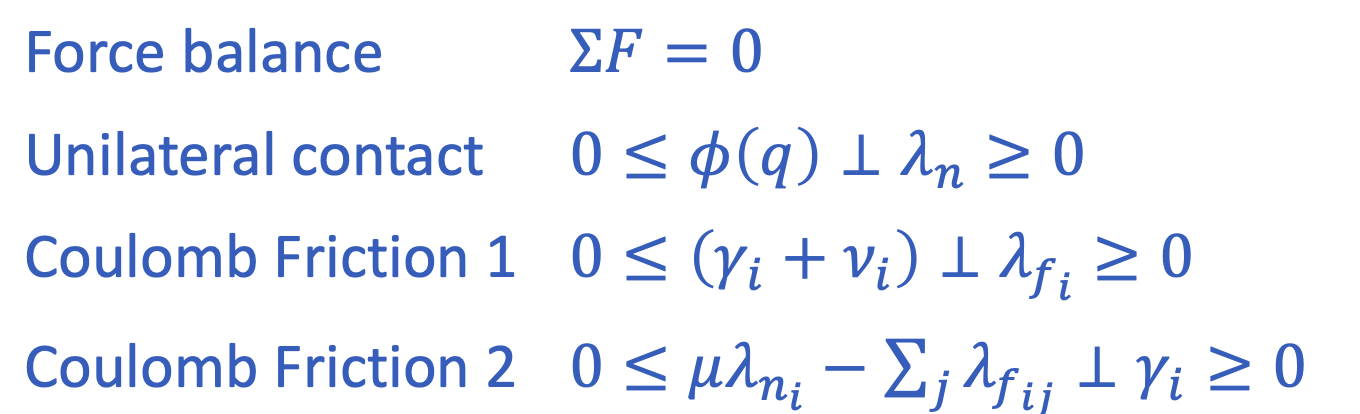
KKT condition of a convex QP.
- These are the standard LCP constraints for rigid mulitbody simulation, typically attributed to Stewart, Trinkle and Anitescu.
Anitescu, Mihai, and Florian A. Potra. "Formulating dynamic multi-rigid-body contact problems with friction as solvable linear complementarity problems." Nonlinear Dynamics 14.3 (1997): 231-247.
Stewart, David E. "Rigid-body dynamics with friction and impact." SIAM review 42.1 (2000): 3-39.
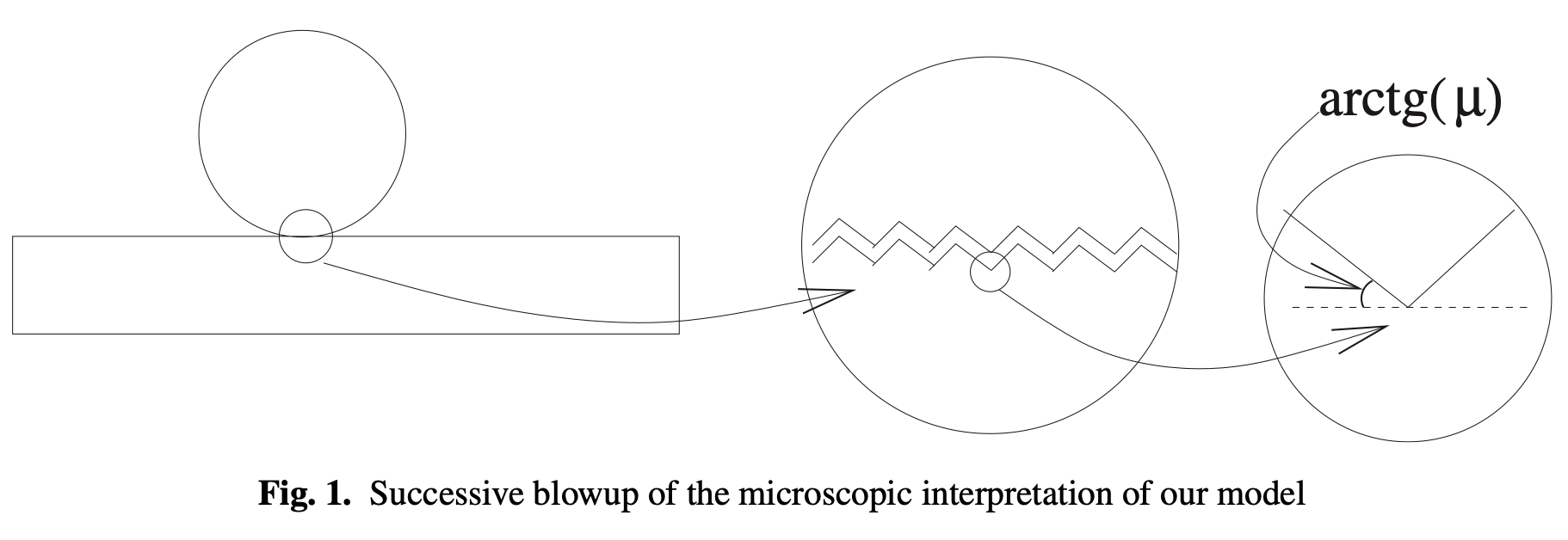
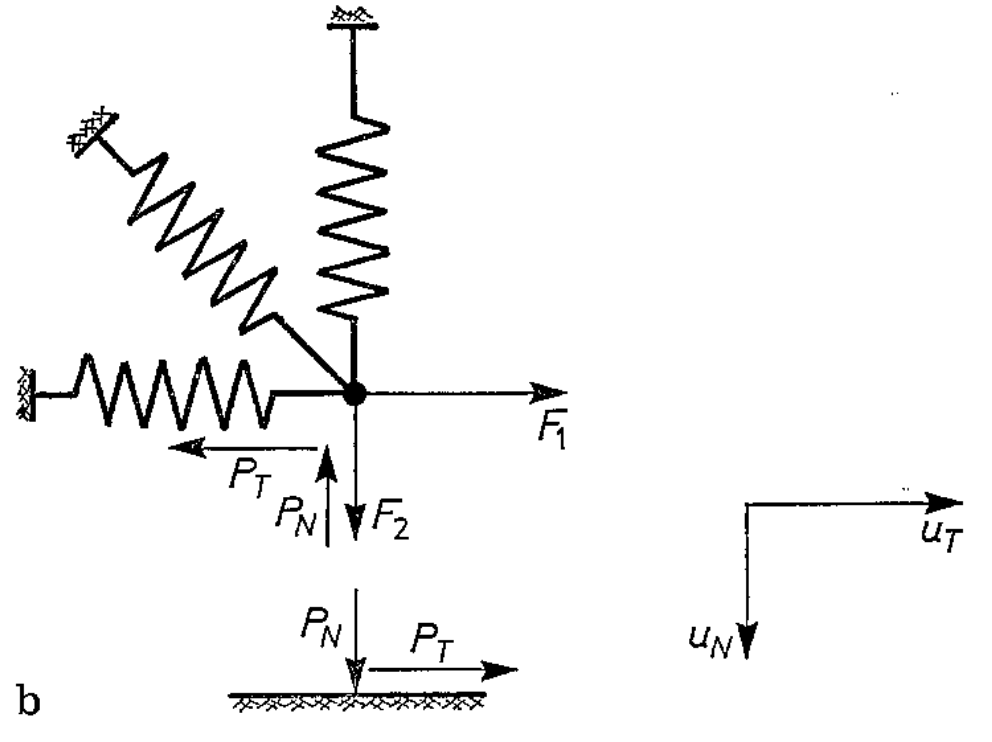
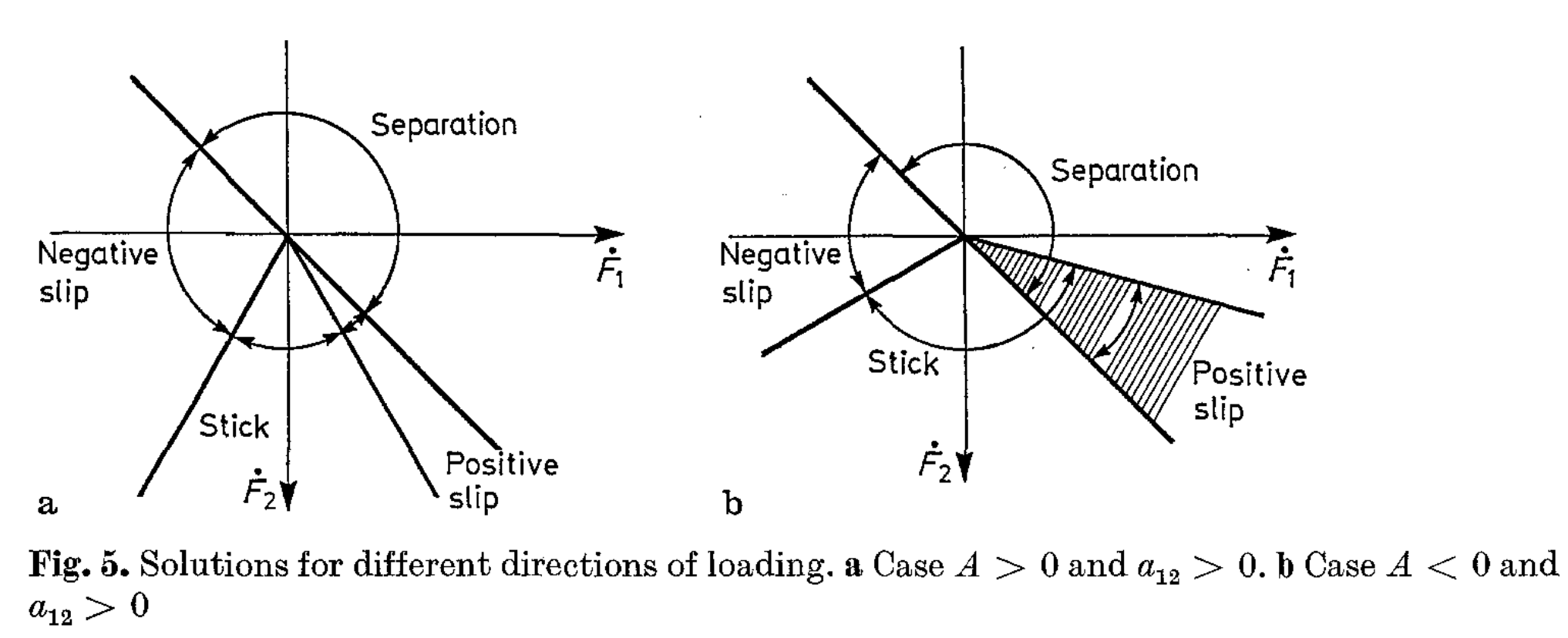
Modeling Coulomb friction as a convex program
- Anitescu proposed a relaxation of the standard complementarity constraints for frictional contacts.
- Example: frictional contact \(i\) in 2D with friction coefficient \(\mu_i\):
Anitescu, Mihai. "Optimization-based simulation of nonsmooth rigid multibody dynamics." Mathematical Programming 105.1 (2006): 113-143.
\beta_{i1}
\beta_{i2}
\mu \beta_{i1}
\mu \beta_{i2}
contact force
h(v_{n_i} - \mu_i v_{d_i}) + \phi_i \geq 0
h(v_{n_i} + \mu_i v_{d_i}) + \phi_i\geq 0
\text{force} \propto \beta_{i2}
\text{force} \propto \beta_{i1}
\bm{\mathsf{n}}_i
\bm{\mathsf{d}}_{i2}
\bm{\mathsf{d}}_{i1}
0 \leq \beta_{i1} \perp h(v_{n_i} + \mu_i v_{d_i}) + \phi_i \geq 0,\\
0 \leq \beta_{i2} \perp h(v_{n_i} - \mu_i v_{d_i}) + \phi_i \geq 0.
Forces along extreme rays of the friction cone.
Signed distance at the current time step.
Translation along the extreme rays.
Time step.
\phi_i = 0
Anitescu's constraints
- are the same as the standard complementarity constraints when the contact is not sliding.
- creates a gap between two objects when they are sliding relative to each other.
Modeling Coulomb friction as a convex program
Standard LCP (a)
Anitescu (b)
Modeling Coulomb friction as a convex program
0 \leq \beta_{i1} \perp h(v_{n_i} + \mu_i v_{d_i}) + \phi_i \geq 0,\\
0 \leq \beta_{i2} \perp h(v_{n_i} - \mu_i v_{d_i}) + \phi_i \geq 0.
A friction cone with 2 extreme rays:
A friction cone with \(n_d\) extreme rays:
0 \leq \beta_{ij} \perp \left(J_{n_i} + \mu_i J_{d_{ij}}\right)v + \phi_i / h \geq 0, \forall j = 1 \dots n_d.
Jacobians along the contact normal.
Jacobian along the contact tangents.
Generalized velocity of the system.
M(q)(v' - v) = -hC(q, v) + h\tau_g + h\tau_a + \sum_{ij} \left(J_{n_i} + \mu_i J_{d_{ij}}\right)^\intercal \beta_{ij} \\
\text{subject to} \\
0 \leq \beta_{ij} \perp \left(J_{n_i} + \mu_i J_{d_{ij}}\right)v + \phi_i / h \geq 0, \forall j = 1 \dots n_d.
Newton's second law with contact becomes:
Coriolis
gravity
contact
mass
velocity, next step
velocity, current
configuration, current
which are the KKT conditions of the following convex QP:
actuation
J_{ij}
\underset{v'}{\min} \; \frac{1}{2} v'^\intercal M v' + \left(-h\tau_g - h\tau_a - Mv + hC \right)^\intercal v'\\
\text{subject to} \\
\frac{\phi_i}{h} + J_{ij} v' \geq 0, \forall i, j.
contact index.
Extreme ray index.
Anitescu, Mihai. "Optimization-based simulation of nonsmooth rigid multibody dynamics." Mathematical Programming 105.1 (2006): 113-143.
Specializing to robotic manipulation
- Things move slowly (quasistatic)
- Robots can be modeled as impedances, which become springs under the quasistatic assumption.
- Treat robots (actuated) and objects (unactuated) differently:
M(q)(v' - v) = -hC(q, v) + h\tau_g + h\tau_a + \sum_{ij} J_{ij}^\intercal \beta_{ij} \\
Coriolis
gravity
contact
mass
actuation
q =
\begin{pmatrix}
q_u \\
q_a
\end{pmatrix},
v =
\begin{pmatrix}
v_u \\
v_a
\end{pmatrix}
\underset{v'}{\min} \; \frac{h^2}{2} v_a'^\intercal K v_a' +
h
\begin{bmatrix}
\tau_{g_u} \\
K_a (\bar{q}_a' - q_a)
\end{bmatrix}^\intercal
\begin{bmatrix}
v_u'\\
v_a'
\end{bmatrix}\\
\text{subject to} \\
\frac{\phi_i}{h} + J_{ij} v' \geq 0, \forall i, j.
\implies 0 = h\tau_{g_u} + \sum_{ij} J_{ij}^\intercal \beta_{ij} \\
Objects dynamics:
\tau_a = 0
- Dynamics of the entire system is given by the KKT conditions of
\tau_a = K_a \left(\bar{q}_a' - (q_a + h v_a') \right) - \tau_g
Robot dynamics:
Commanded joint angles at the next time step.
Gravity compensation
\implies 0 = hK_a \left(\bar{q}_a' - (q_a + h v_a') \right) + \sum_{ij} J_{ij}^\intercal \beta_{ij} \\
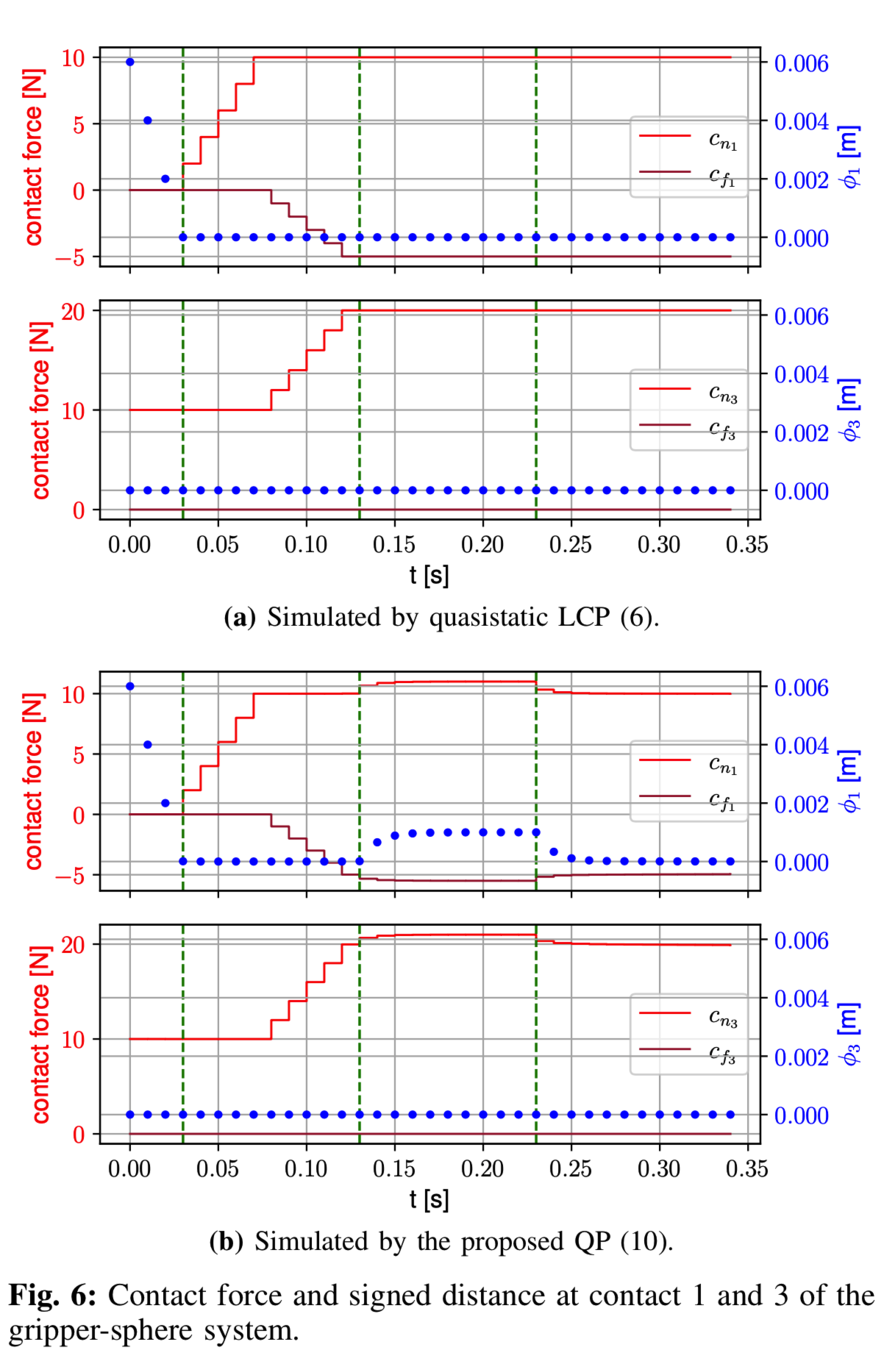
Simulation results
- The Anitescu contact model and the quasistatic simplification allows much larger simulation time steps.
Quasistatic, h = 0.1s.
MBP, h = 1e-3s.
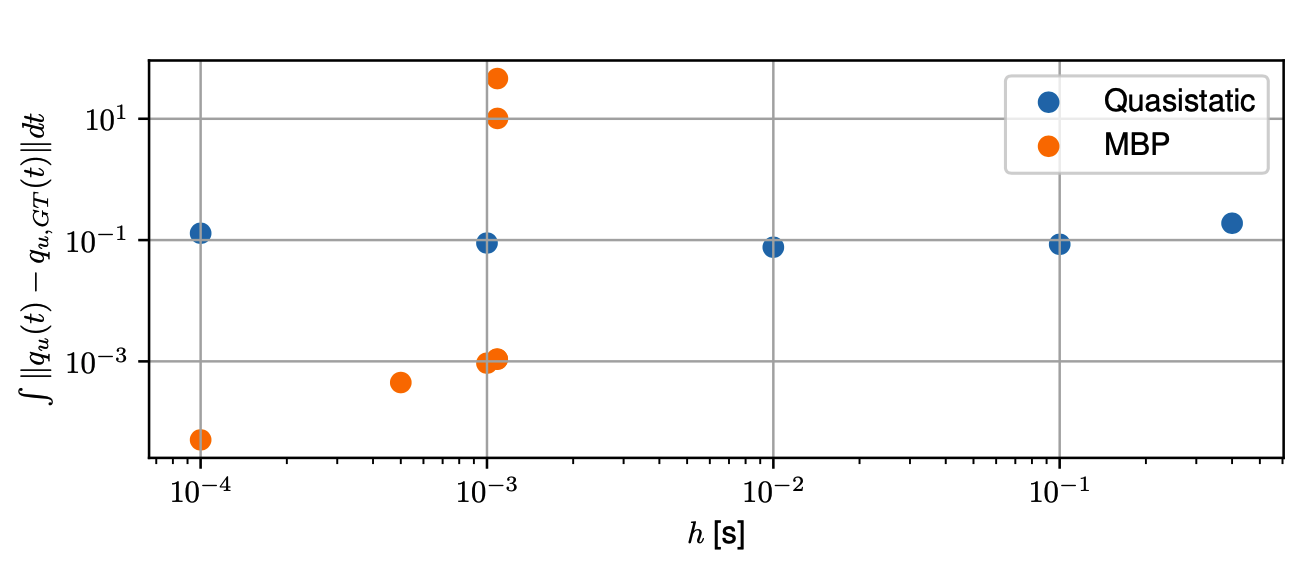
Integral error vs. simulation time step
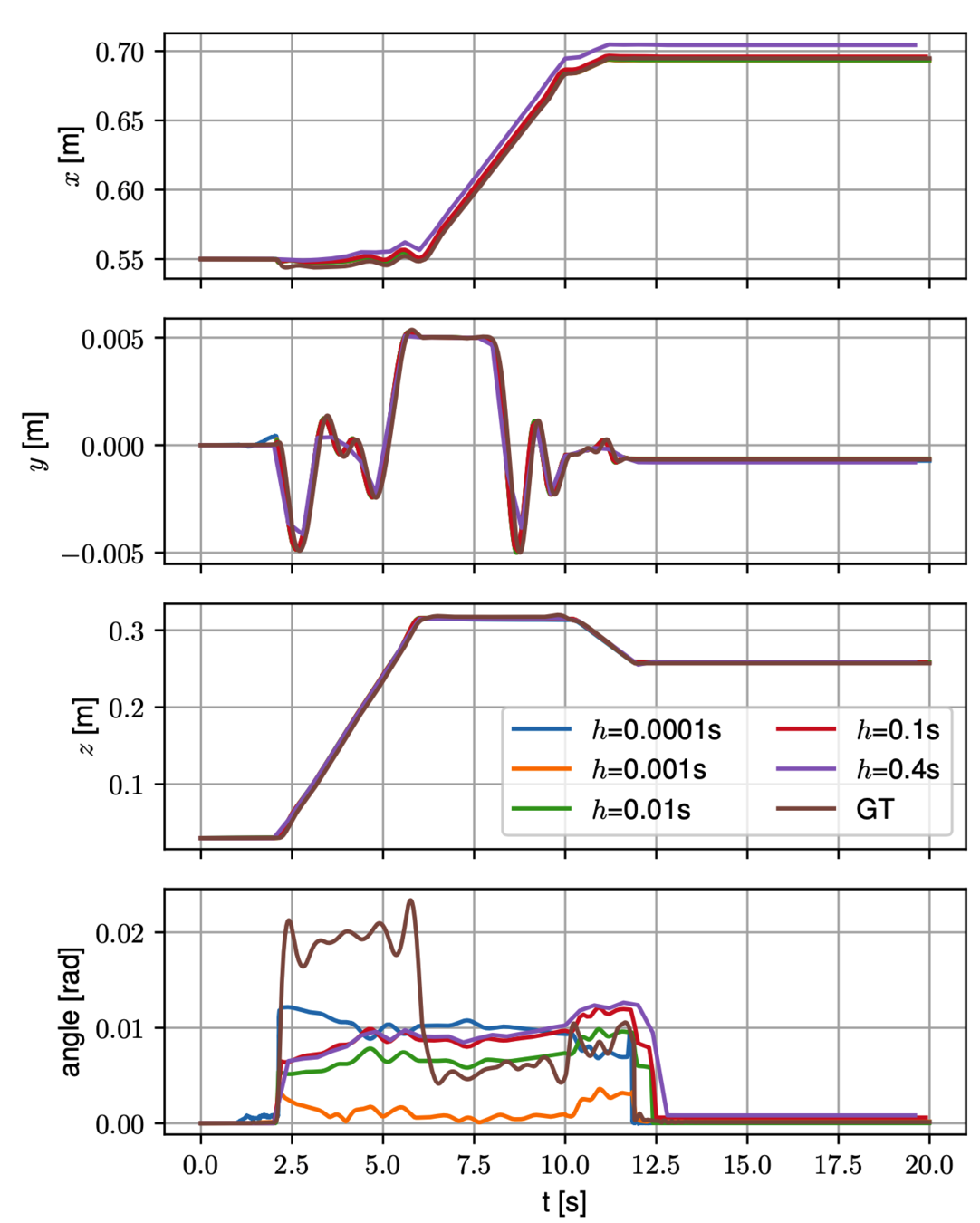
Pose trajectory of the red box.
- Ground truth trajectory is generated by Drake's MultibodyPlant with h=5e-5.
Conclusion
- A fast convex time-stepping scheme for rigid multi-body systems with frictional contacts, which combines
- Anitescu's frictional constraints
- Simplifying quasstatic assumptions.
- Large increase in simulation time step, which not only makes simulation faster, but also increases the horizon of planning algorithms using the proposed dynamics model.
Backup slides
Simulating contacts
- In the frictionless case, we do not need to write down complementarity constraints explicitly.
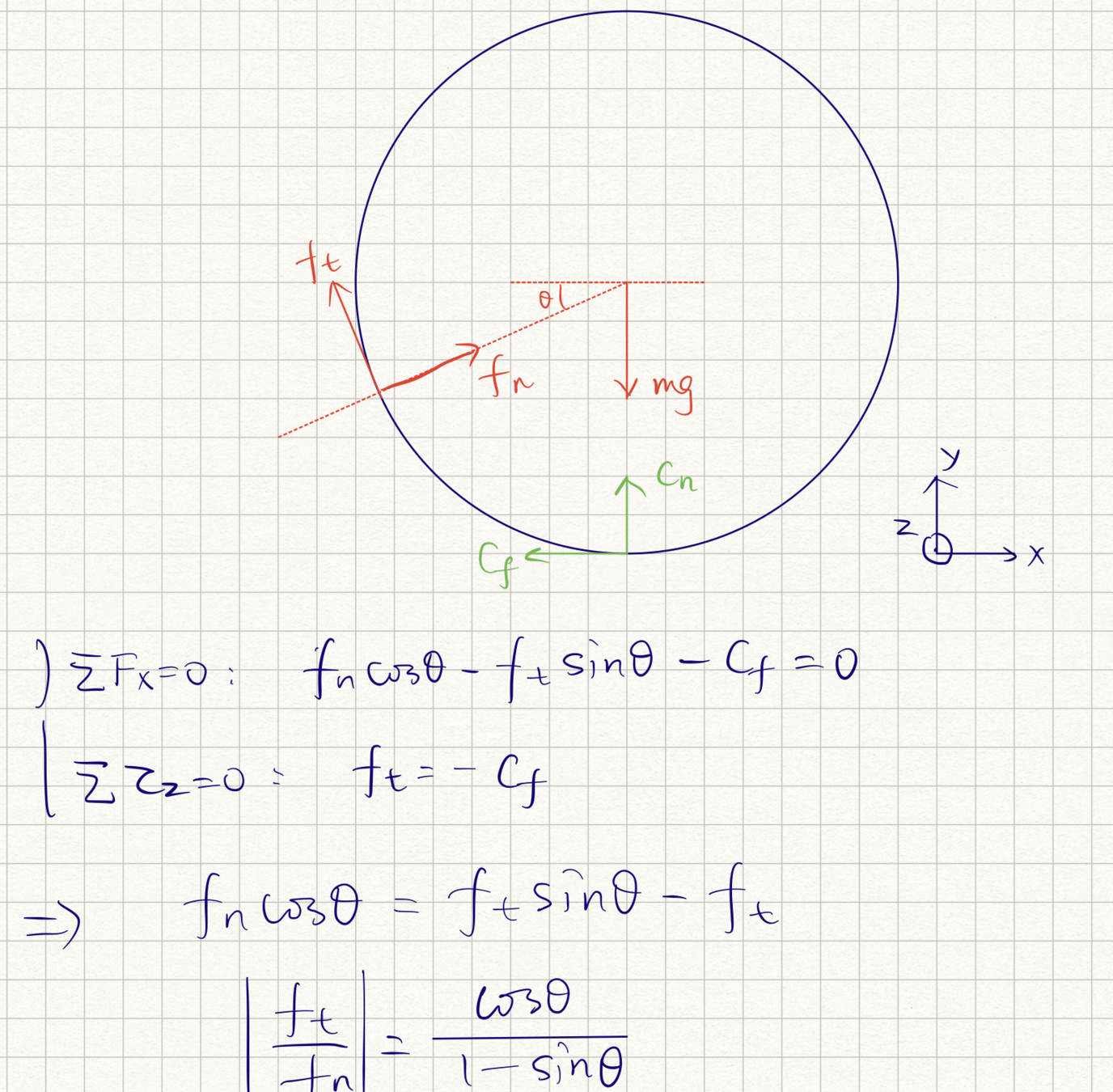
- Example from Boyd's convex optimization textbook: find the stable configuration of the following system:
- KKT conditions of the above QP include
- Contact forces (\(\lambda_1, \lambda_2, \lambda_3\)) emerge as Lagrange multipliers of the non-penetration constraints.
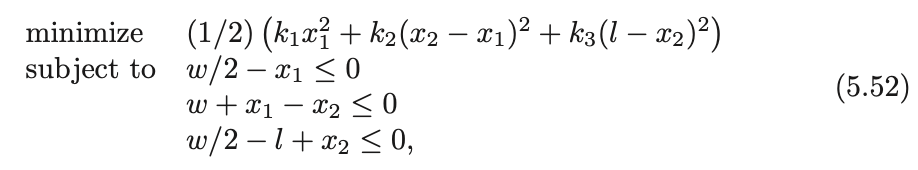
Potential energy of the system.
Non-penetration constraints.
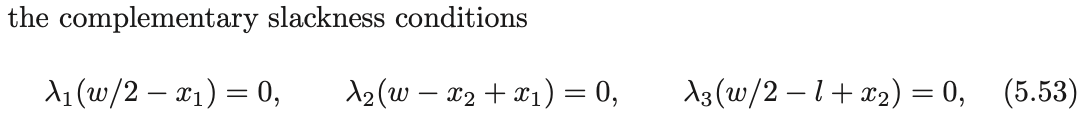
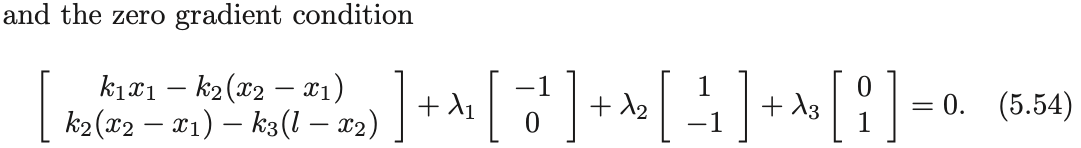
Force balance of all boxes.
Unilateral contact constraints.
Modeling Coulomb friction as a convex program
- MuJoCo also solves multi-body contact forward simulation as a convex QP, but doesn't accurately model contact forces.
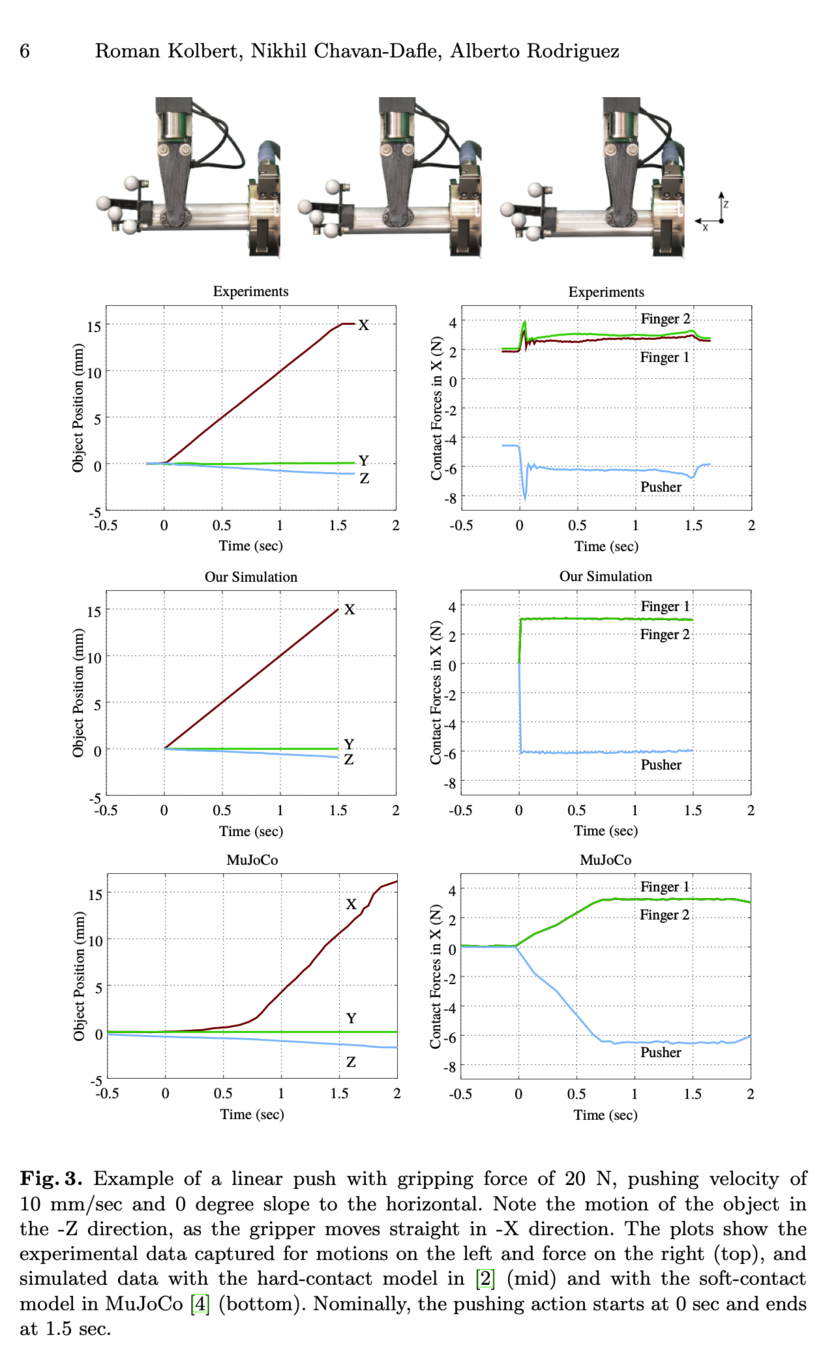
Kolbert, Roman, Nikhil Chavan-Dafle, and Alberto Rodriguez. "Experimental validation of contact dynamics for in-hand manipulation." International Symposium on Experimental Robotics. Springer, Cham, 2016.
standard LCP contact model
Drawbacks of the quasistatic assumption.
- Cannot simulate dropping.
- Cannot simulate rolling a sphere on a flat surface.
Drawbacks of the quasistatic assumption.
- Solutions may not be unique.
- The quadratic form in the cost of the QP is positive semi-definite.
\underset{v'}{\min} \; \frac{h^2}{2} v_a'^\intercal K v_a' +
h
\begin{bmatrix}
\tau_{g_u} \\
K_a (\bar{q}_a' - q_a)
\end{bmatrix}^\intercal
\begin{bmatrix}
v_u'\\
v_a'
\end{bmatrix}\\
\text{subject to} \\
\frac{\phi_i}{h} + J_{ij} v' \geq 0, \forall i, j.
Specializing to robotic manipulation, take 2.
- Robots are still impedance-controlled and modeled as springs.
- Objects are quasi-dynamic.
- First proposed by Matt Mason: objects move slowly and "in the direction of acceleration".
- An impulse-momentum interpretation better illustrates why it's a good idea.
M(q)(v' - v) = -hC(q, v) + h\tau_g + h\tau_a + \sum_{ij} J_{ij}^\intercal \beta_{ij} \\
Coriolis
gravity
contact
mass
actuation
\underset{v'}{\min} \; \frac{1}{2}
\begin{bmatrix}
v_u'\\
v_a'
\end{bmatrix}^\intercal
\begin{bmatrix}
M_u & 0 \\
0 & h^2K_a
\end{bmatrix}
\begin{bmatrix}
v_u'\\
v_a'
\end{bmatrix}
+
h
\begin{bmatrix}
\tau_{g_u} \\
K_a (\bar{q}_a' - q_a)
\end{bmatrix}^\intercal
\begin{bmatrix}
v_u'\\
v_a'
\end{bmatrix}\\
\text{subject to} \\
\frac{\phi_i}{h} + J_{ij} v' \geq 0, \forall i, j.
- Dynamics of the entire system is given by the KKT conditions of
Robot dynamics:
\tau_a = K_a \left(\bar{q}_a' - (q_a + h v_a') \right) - \tau_g\\
M_a(v_a' - v_a) = 0
\implies 0 = hK_a \left(\bar{q}_a' - (q_a + h v_a') \right) + \sum_{ij} J_{ij}^\intercal \beta_{ij} \\
Objects dynamics:
\tau_a = 0 \\
v_u = 0
\implies M_u v_u' = \tau_{g_u} + \sum_{ij} J_{ij}^\intercal \beta_{ij} \\
- Impulses that cannot be balanced are converted into momentum.
- The momentum is thrown away at the next time step.
- Introduces a lot of damping, which seems reasonable for manipulation.
Simulation results
Quasistatic sphere pushing
Quasi-dynamic sphere pushing
Quasi-dynamic dropping
- Also works for more complex systems (e.g. the example at the beginning)!
quasistatic_sim_ICRA21
By Pang
