Research Highlights
Pang
Planning and Control for Contact-rich Robotic Manipulation
- RRT and Trajectory optimization for dexterous hands (>16DOF).
- RRT takes less than a minute.
- Trajectory optimization is fast, and only needs trivial initialization.
- Our tasks are challenging for existing model-based methods.
- Contact-implicit traj-opt: huge NLP with many local minima.
- Hybrid dynamics / Mixed-integer: too many contact modes.

- Impressive demo.
- Lots of offline computation.
- Policy is hard to interpret.
Why did our method work?
- a Convex, Quasi-dynamic Differentiable Simulator
- \(F = ma\) --> \(F = 0\) (almost)
- Considers only transitions between equilibriums, ignores transient effects such as damping.
- Achieves stable integration with much larger time steps. (0.001s --> 0.4s)
-
Convex approximation of contact dynamics (Anitescu).
- Easier than Nonlinear Complementarity Programs (NCPs).
- The extent of relaxation is controlled by a single hyperparameter.
- Differentiable by differentiating through the KKT conditions of a convex program.
- \(F = ma\) --> \(F = 0\) (almost)
- Randomized Smoothing --> Deterministic Smoothing.
- Contact dynamics is non-smooth (\(C^0\)).
- We showed sampling, which RL does a lot, makes contact dynamics smoother (\(C^1\)).
- Our differentiable simulator can be smoothed without sampling, thereby accelerating algorithms that use smoothed gradients.
-
The planned trajectories are already stabilizable in Drake!
- which means our simplification of contact dynamics is reasonable.

Before my PhD defense...

Stabilize this with linear control / MPC!
After my PhD defense... dexterous manipulation of arbitrary rigid objects
Robust planning and control.
- Robust planning/control
- Different object sizes / friction coefficients
- Perception /control based-on tactile sensors
- No occlusion.
- Enable force feedback.

Reinforcement Learning.
- Marco Hutter's work on Anymal has been a great inspiration.
- Trying their strategy, but with tweaks for manipulation.
- Cannot use cyclic policy for leg motions.
- Need to consider information about object?
- Trying their strategy, but with tweaks for manipulation.
- Can our model-based approach lead to easier-to-learn policy parameterization?
- RRT does sampling, but only remembers the samples. Can learning offer a better way to use the samples?
- Instead of learning joint angle commands, can we learn delta object pose, and use a robust model-based controller to achieve the delta pose?
State representation for dexterous manipulation.
- When we close our eyes with an object in our hand, we don't need the pose of the object to locally manipulate it.
- Are local contact patches sufficient?
Turning the ball by 30 degrees: open-loop
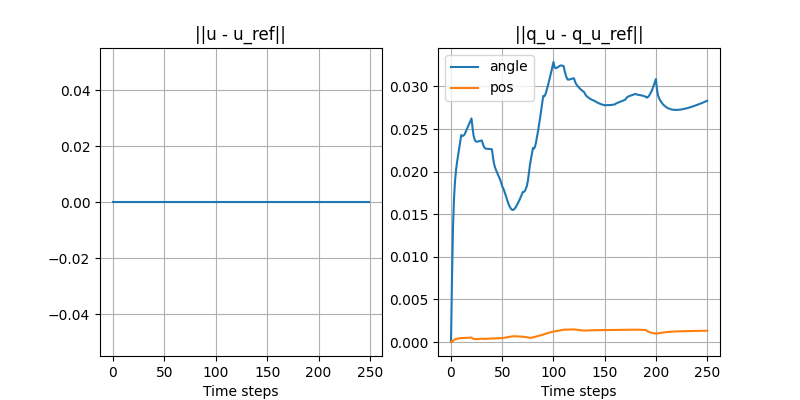
- Simulated in Drake with the same SDF as the quasi-dynamic model used for planning.
Turning the ball by 30 degrees: open-loop with disturbance
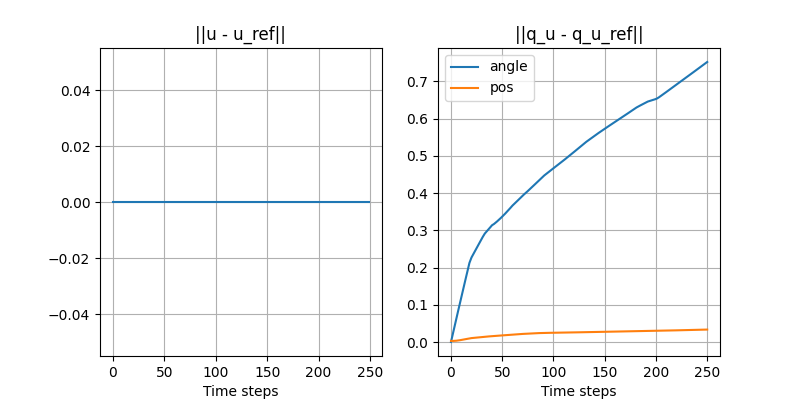
- Initial position of the ball is off by 3mm.
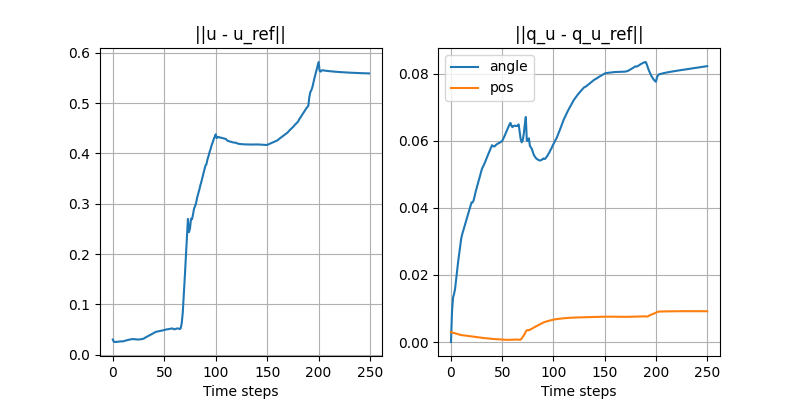
Turning the ball by 30 degrees: closed-loop with disturbance
- Initial position of the ball is off by 3mm.
- Simple controller:
\begin{aligned}
\underset{q^\mathrm{u}_+, u}{\min} &\|q_+^\mathrm{u} - q_+^\mathrm{u, ref}\|_\mathbf{Q} + \|u - u^\mathrm{ref} \|_\mathbf{R}, \text{s.t.}\\
& q^\mathrm{u}_+ = \mathbf{A}_\rho^\mathrm{u} q^\mathrm{u} + \mathbf{B}_\rho^\mathrm{u} u
\end{aligned}
Smooth linearization
Task: turning the ball by 30 degrees.
research_highlights
By Pang
research_highlights
- 162



